https___authedu.mosreg.ru_ej_attachments_files_053_506_042_original_%D0%9F%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F%20%D0%BF%D0%BE%20%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5%

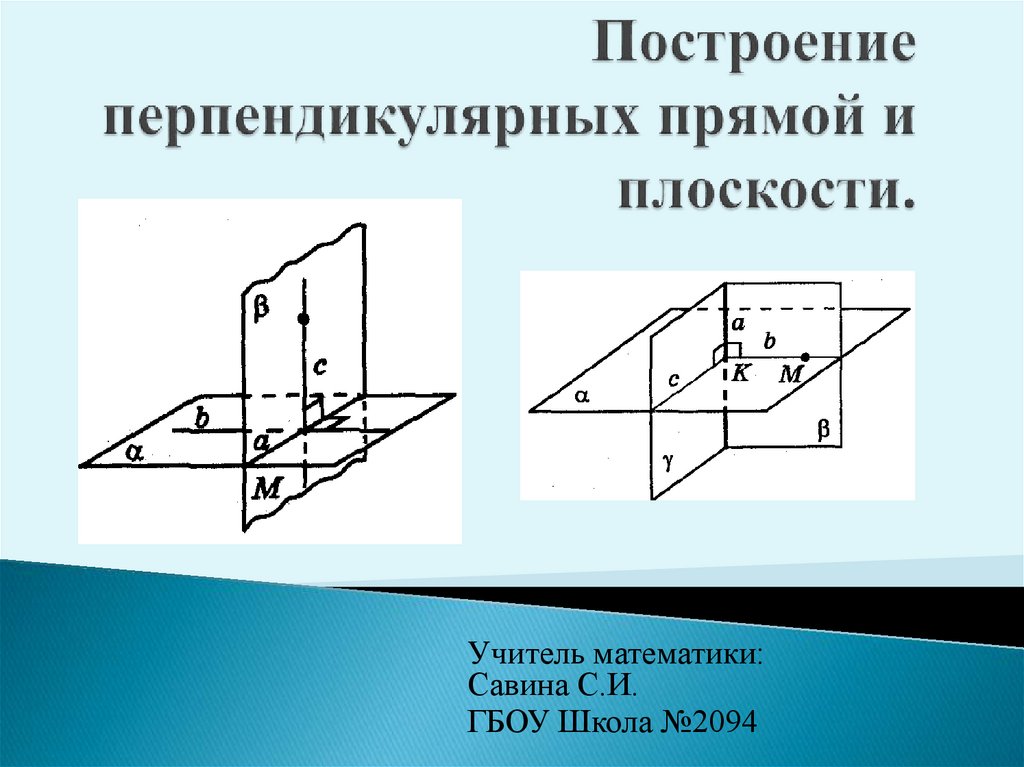
1. Построение перпендикулярных прямой и плоскости.

Учитель математики:
Савина С.И.
ГБОУ Школа №2094

2. Решим две задачи.

ЗАДАЧА 1. Через данную точку М провести
плоскость ɑ, перпендикулярную данной
прямой а.
В решении возможны два случая:
1)точка М не принадлежит данной прямой а;
2) точка М принадлежит данной прямой а.

3.

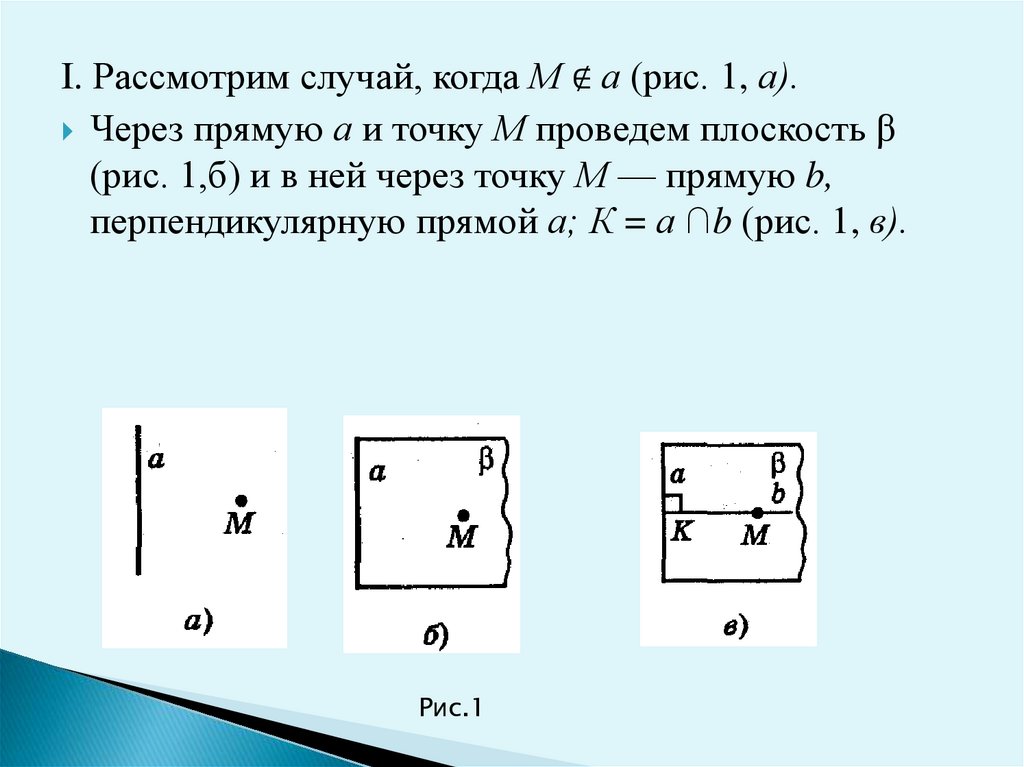
I. Рассмотрим случай, когда М ∉ а (рис. 1, а).
Через прямую а и точку М проведем плоскость β
(рис. 1,б) и в ней через точку М — прямую b,
перпендикулярную прямой а; К = а ∩b (рис. 1, в).
Рис.1

4.

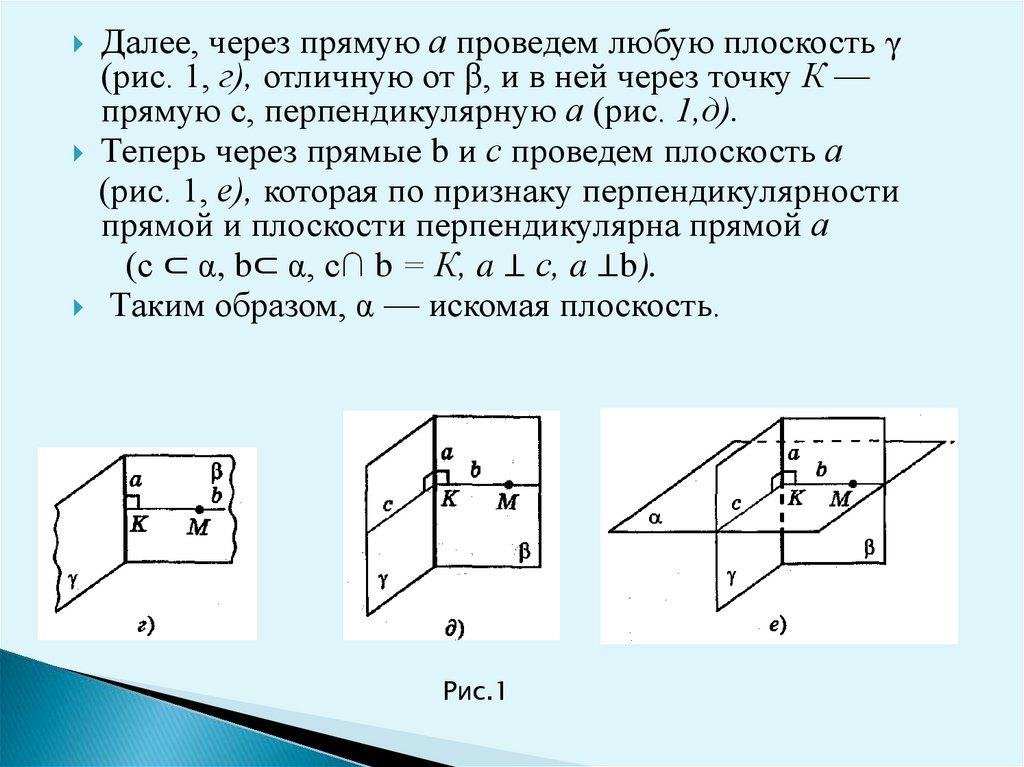
Далее, через прямую а проведем любую плоскость γ
(рис. 1, г), отличную от β, и в ней через точку К —
прямую с, перпендикулярную а (рис. 1,д).
Теперь через прямые b и с проведем плоскость а
(рис. 1, е), которая по признаку перпендикулярности
прямой и плоскости перпендикулярна прямой а
(с ⊂ α, b⊂ α, с∩ b = К, a ⊥ с, a ⊥b).
Таким образом, α — искомая плоскость.
Рис.1

5. Докажем, что α— единственная плоскость, удовлетворяющая условию задачи.

Предположим, что через точку М
можно провести другую плоскость,
например α1 перпендикулярную
прямой а (рис. 2). Тогда плоскости
α1 и β, имея общую точку М,
пересекаются по некоторой прямой
b1, которая перпендикулярна
прямой a (a ⊥α1, b1⊂ α1).
Получили: в плоскости β через
точку М проходят две прямые b и
b1, перпендикулярные прямой а,
что невозможно. Следовательно,
наше предположение неверно, и
плоскость α единственна.
Рис.2

6.

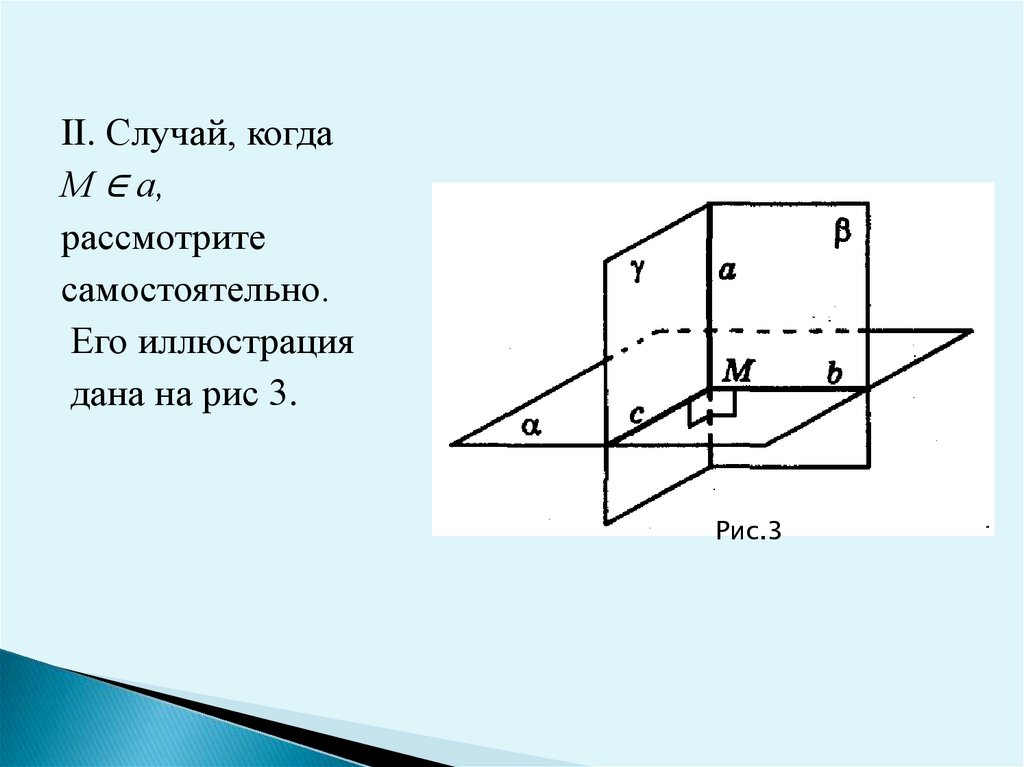
II. Случай, когда
М ∈ а,
рассмотрите
самостоятельно.
Его иллюстрация
дана на рис 3.
Рис.3

7.

ЗАДАЧА 2. Через данную точку М провести
прямую а, перпендикулярную данной плоскости α.
В решении возможны два случая:
1)точка М принадлежит плоскости α;
2) точка М не принадлежит плоскости α.

8.

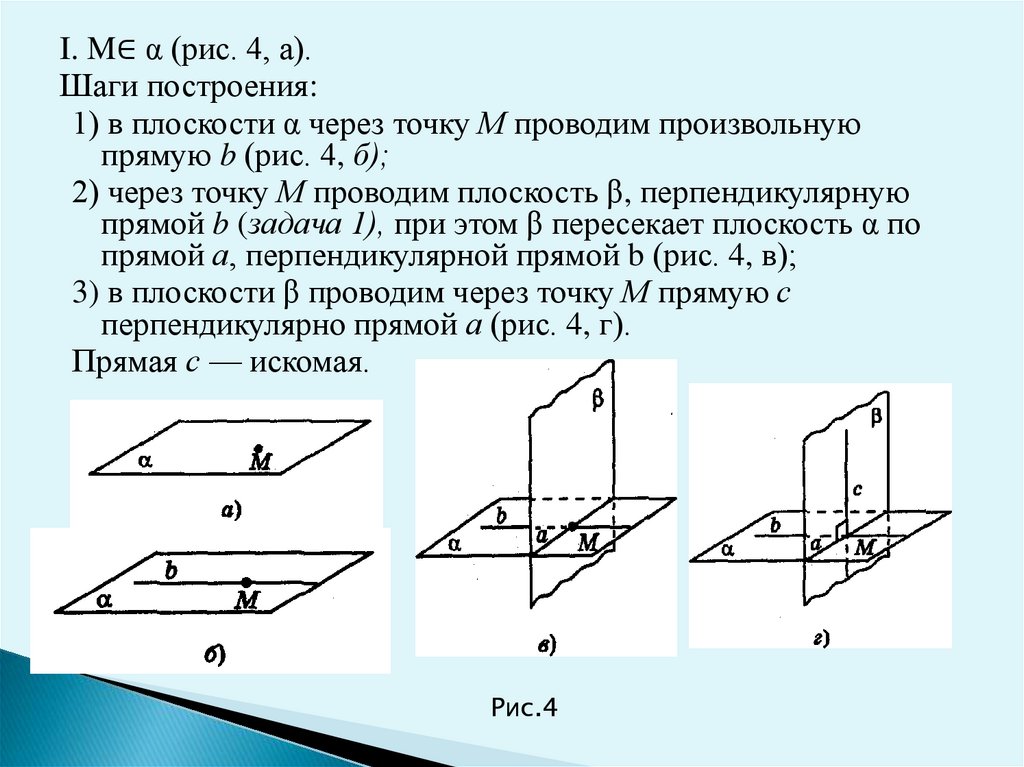
I. M∈ α (рис. 4, а).
Шаги построения:
1) в плоскости α через точку М проводим произвольную
прямую b (рис. 4, б);
2) через точку М проводим плоскость β, перпендикулярную
прямой b (задача 1), при этом β пересекает плоскость α по
прямой а, перпендикулярной прямой b (рис. 4, в);
3) в плоскости β проводим через точку М прямую с
перпендикулярно прямой а (рис. 4, г).
Прямая с — искомая.
Рис.4

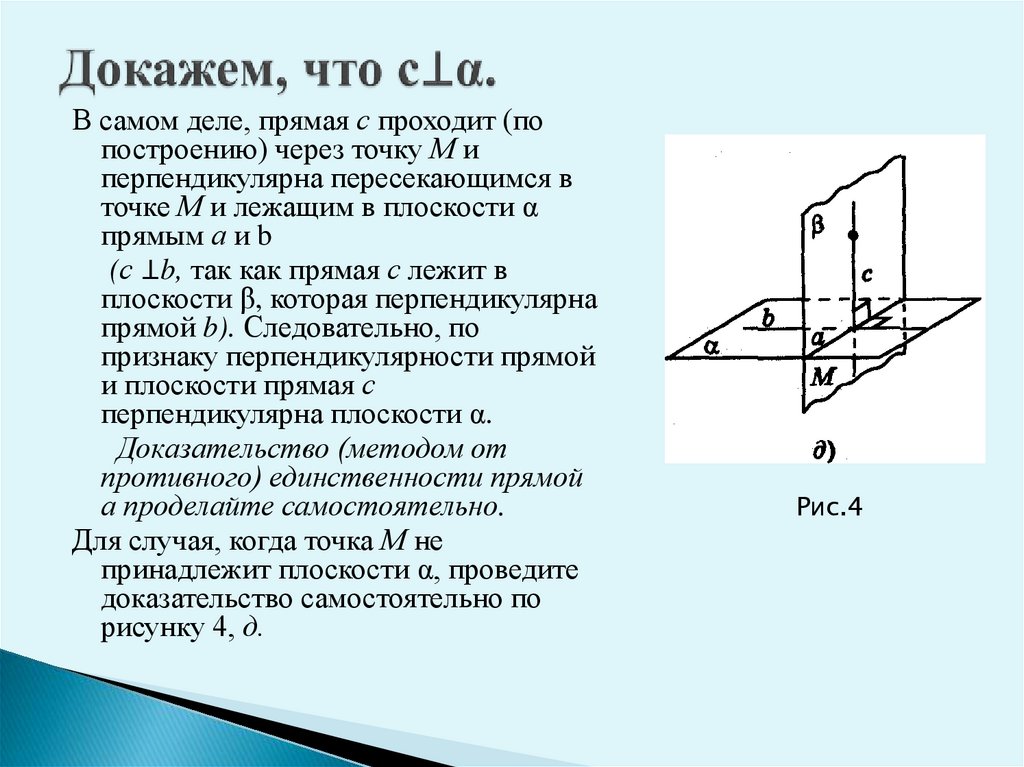
9. Докажем, что с⊥α.

В самом деле, прямая с проходит (по
построению) через точку М и
перпендикулярна пересекающимся в
точке М и лежащим в плоскости α
прямым а и b
(с ⊥b, так как прямая с лежит в
плоскости β, которая перпендикулярна
прямой b). Следовательно, по
признаку перпендикулярности прямой
и плоскости прямая с
перпендикулярна плоскости α.
Доказательство (методом от
противного) единственности прямой
а проделайте самостоятельно.
Для случая, когда точка М не
принадлежит плоскости α, проведите
доказательство самостоятельно по
рисунку 4, д.
Рис.4

10. Обобщая вышесказанное, отметим, что:

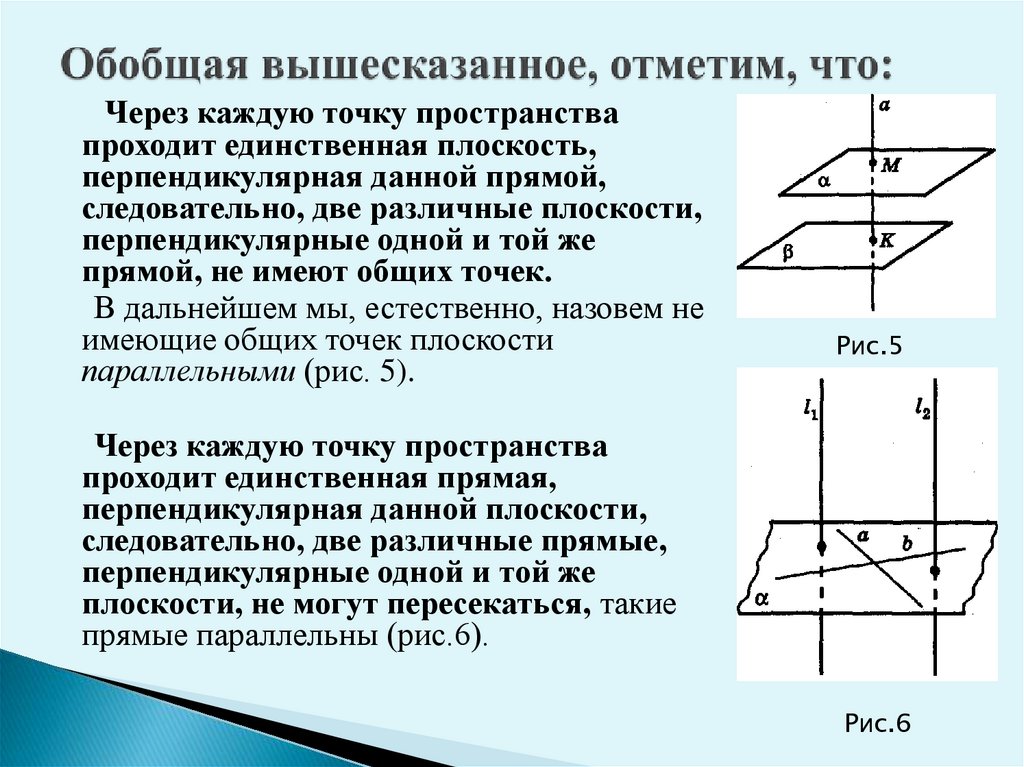
Через каждую точку пространства
проходит единственная плоскость,
перпендикулярная данной прямой,
следовательно, две различные плоскости,
перпендикулярные одной и той же
прямой, не имеют общих точек.
В дальнейшем мы, естественно, назовем не
имеющие общих точек плоскости
параллельными (рис. 5).
Рис.5
Через каждую точку пространства
проходит единственная прямая,
перпендикулярная данной плоскости,
следовательно, две различные прямые,
перпендикулярные одной и той же
плоскости, не могут пересекаться, такие
прямые параллельны (рис.6).
Рис.6

11. Используемая литература.

Потоскуев Е. В.
Геометрия 10 кл.: Учеб. Для общеобразоват.
Учреждений с углубл. И профильным
изучением математики/ Е. В. Потоскуев, Л. И.
Звавич.-М.: Дрофа,2004.