Пифахор

1.

Пифагор
Кто такой Пифагор, история
создания Теоремы Пифагора
Аутов Самир

2.

Пифагор
План презентации:
I. Введение
II. Кто такой Пифагор
III. Пифагорейская школа
IV. Теорема Пифагора
V. История появление теоремы
VI. Доказательства теоремы
VII. Применение теоремы Пифагора

3.

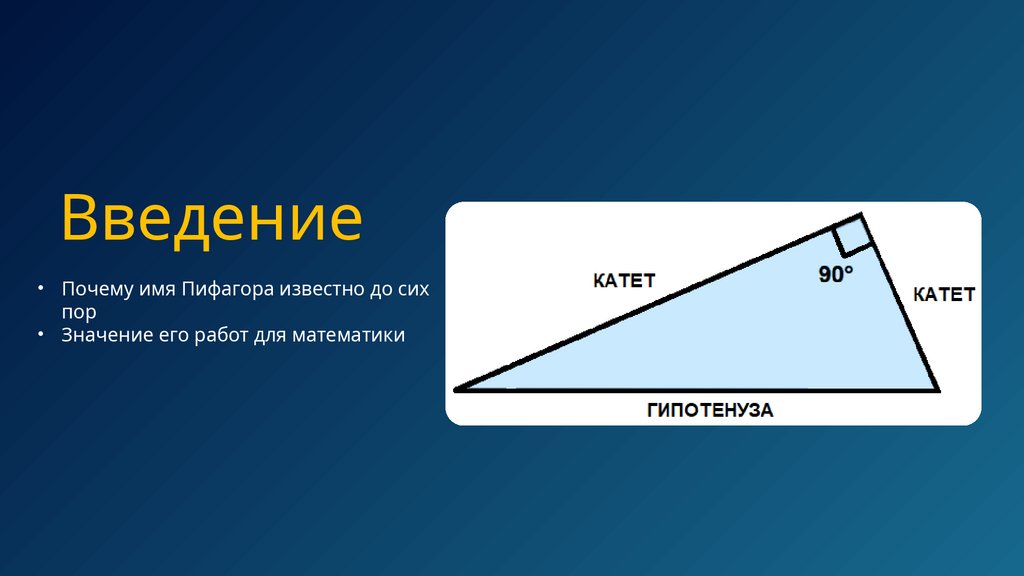
Введение
• Почему имя Пифагора известно до сих
пор
• Значение его работ для математики

4.

Имя Пифагора(греч.
Πυθαγόρας)
известно до
Почему
имя Пифагора
известно
досихсих
пор, потому что оно связано с одним из самых
пор
базовых и узнаваемых знаний, которые изучают
люди по всему миру ещё со школы. Его имя
постоянно повторяется в учебниках, на уроках и
в образовании в целом, поэтому оно прочно
закрепилось в истории и памяти человечества.
Кроме этого, Пифагор был не просто учёным, а
основателем целого учения. Его идеи о порядке,
логике и объяснении мира через разум
повлияли на развитие науки и философии, а
ученики сохранили и распространили его
взгляды. Благодаря этому Пифагор стал
символом науки Древней Греции и остаётся
известным спустя тысячелетия.

5.

Работы Пифагора и его школы заложили основы
Значение
его работ для
математического мышления. Они показали, что
математики
математика — это не просто счёт для
практических нужд, а наука, основанная на
логике, порядке и строгих рассуждениях. Именно
пифагорейцы начали рассматривать
доказательство как обязательную часть
математики, а не просто получение ответа.
Кроме того, его идеи повлияли на развитие
геометрии и теории чисел. Математика стала
восприниматься как универсальный язык, с
помощью которого можно описывать законы
природы, формы и соотношения. Это понимание
определило дальнейшее развитие всей
математики и стало фундаментом для науки в
целом.

6.

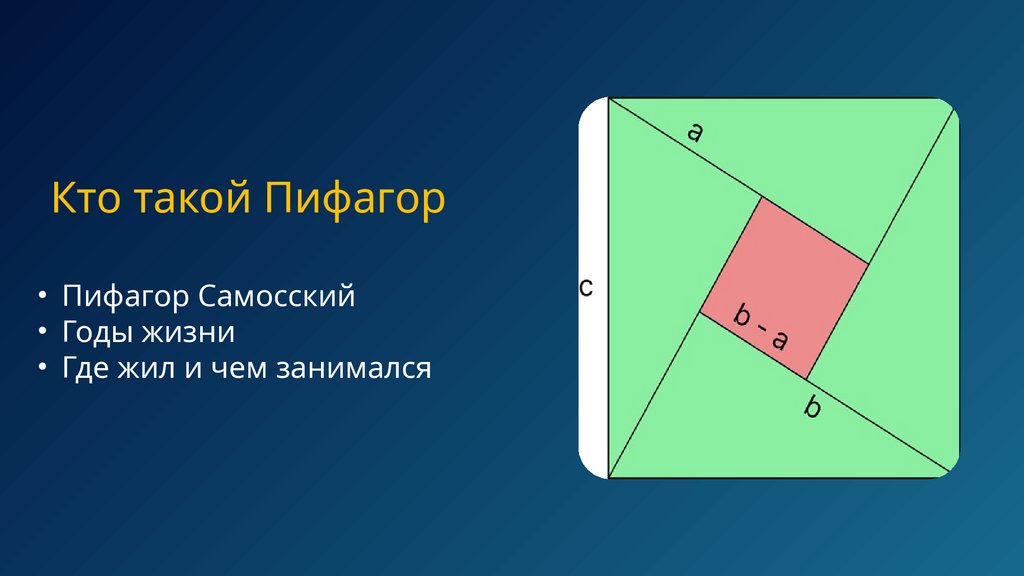
Кто такой Пифагор
• Пифагор Самосский
• Годы жизни
• Где жил и чем занимался

7.

Пифагор
Самосский
Пифагор Самосский
родился около 570 года до н.
э. на острове Самос в Эгейском море (Древняя
Греция).
Отец: Мнесарх - по преданию, резчик по камню
или торговец.
Мать: Пифаида (Пифаис) - уроженка Самоса.
Точные сведения о его семье ограничены, так
как биография Пифагора дошла до нас в
основном из поздних источников и частично
носит легендарный характер.

8.

Точные годы жизни Пифагора Самосского
Годы
жизни
неизвестны, так как он жил в VI–V веках до н. э., а
достоверных документов того времени почти не
сохранилось. Историки опираются на античные
источники (Гераклит, Аристотель, Диоген
Лаэртский), которые часто расходятся между
собой.
Считается, что Пифагор родился около 570 года
до н. э. на острове Самос. В молодости он много
путешествовал: по преданиям, бывал в Египте и
Вавилоне, где изучал математику, астрономию и
философию. Около 530 года до н. э. он покинул
Самос и поселился в городе Кротон (Южная
Италия), где основал свою школу.
Смерть Пифагора относят к периоду 490–480
годов до н. э. Существуют разные версии: по
одной, он погиб во время политических
конфликтов в Кротоне, по другой — умер в
изгнании в городе Метапонт. Поэтому годы его
жизни указываются приблизительно, но чаще

9.

Пифагор родился на острове Самос (Древняя
Греция), где провёл детство и юность. В
Где
жил и чем занимался
молодости он много путешествовал: по
преданиям, посещал Египет и Вавилон, изучал
математику, астрономию, музыку и философию у
местных жрецов и учёных. Эти знания позже
легли в основу его учения.
Около 530 года до н. э. Пифагор переехал в
Кротон (Южная Италия), где основал
пифагорейскую школу — одновременно
философскую, религиозную и научную общину.
Там он занимался систематизацией знаний,
преподавал математику, изучал числа, их
свойства и связь с гармонией мира, развивал
идеи о порядке и логике, а также обучал
учеников этическим и нравственным принципам
жизни. Помимо науки и философии, школа
Пифагора занималась исследованиями музыки и
пропорций, считая, что числа управляют
гармонией всего мира.

10.

Пифагорейская
школа
• Создание школы
• Основные идеи и
правила
• Роль математики в
учении

11.

Создание школы
Пифагорейская школа была основана
Пифагором примерно в 530 году до н.
э. в городе Кротон (Южная Италия).
Это была не просто школа в
современном смысле — скорее
философско-религиозное
сообщество, где ученики изучали
математику, астрономию, музыку и
философию, а также следовали
определённым этическим и
нравственным правилам.

12.

Основные идеи Пифагора и его школы строились
Основные
идеи и правила
вокруг мысли, что числа лежат в основе всего
мира, а гармония и порядок управляют
природой и жизнью человека. Он считал, что
изучение чисел, их свойств и отношений
помогает понять законы вселенной. Также
Пифагор связывал музыку, геометрию и
астрономию с числами, полагая, что всё
подчинено гармоническим пропорциям.
Школа Пифагора имела строгие правила для
учеников. Они жили вместе в общине,
соблюдали дисциплину, вели аскетический образ
жизни, занимались самосовершенствованием и
изучением наук. Ученикам запрещалось
раскрывать учение посторонним, а также
существовали различные этические запреты,
например, внимание к справедливости,
честности и умеренности в повседневной жизни.
Эти принципы помогали поддерживать порядок
и гармонию внутри школы и способствовали
формированию системы знаний.

13.

Роль математики в
Математика
учении занимала центральное
место в учении Пифагора. Он считал,
что числа и их отношения лежат в
основе всего мира и помогают понять
законы природы, гармонию и
порядок во вселенной. Изучение
чисел, их свойств и закономерностей
позволяло постичь не только
практические вещи, как измерение и
строение, но и философские истины о
мире.
В школе Пифагора математика
использовалась для объяснения
музыки, астрономии и геометрии.
Она формировала логическое
мышление учеников, учила
рассуждать строго и
последовательно, а также стала

14.

Теорема Пифагора
• Формулировка теоремы
• Что такое катеты и
гипотенуза

15.

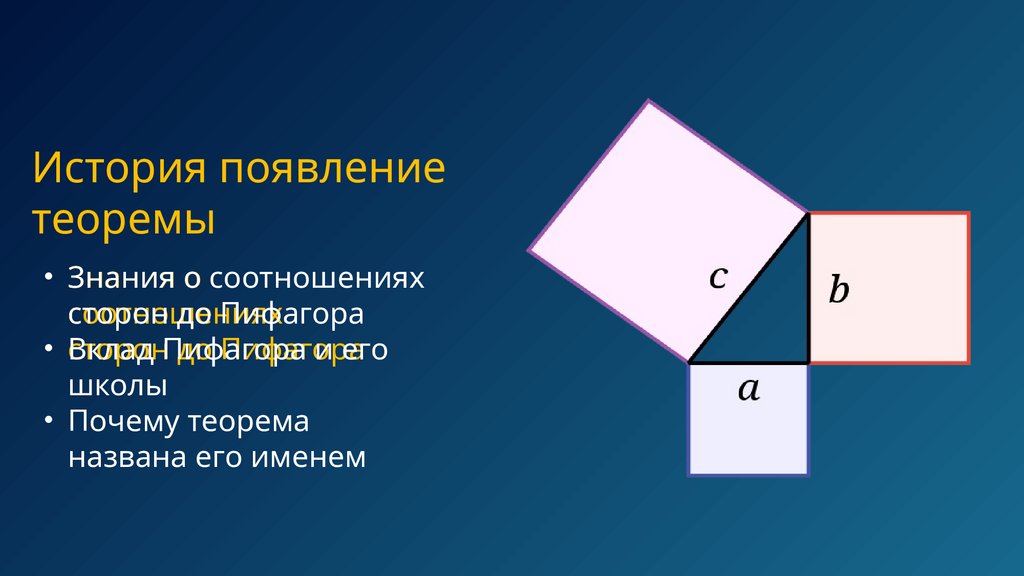
Формулировка теоремы
Теорема Пифагора гласит: в
прямоугольном треугольнике квадрат
длины гипотенузы равен сумме
квадратов длин двух катетов.
Проще говоря, если у треугольника
есть один прямой угол, то сторона,
противоположная этому углу, связана
с другими двумя сторонами
определённым законом. Эта теорема
лежит в основе геометрии и широко
используется для расчётов длин,
расстояний и пропорций.
с² = a²+b²

16.

Что
такое катеты и гипотенуза
В прямоугольном треугольнике две стороны,
которые образуют прямой угол, называются
катетами. То есть это те стороны, которые
встречаются под углом 90 градусов.
Сторона, которая противоположна прямому углу,
называется гипотенузой. Она всегда самая
длинная в прямоугольном треугольнике.
Простыми словами: катеты «строят» прямой угол,
а гипотенуза — соединяет их концы.

17.

История появление
теоремы
• Знания о соотношениях
сторон
соотношениях
до Пифагора
• Вклад
сторонПифагора
до Пифагора
и его
школы
• Почему теорема
названа его именем

18.

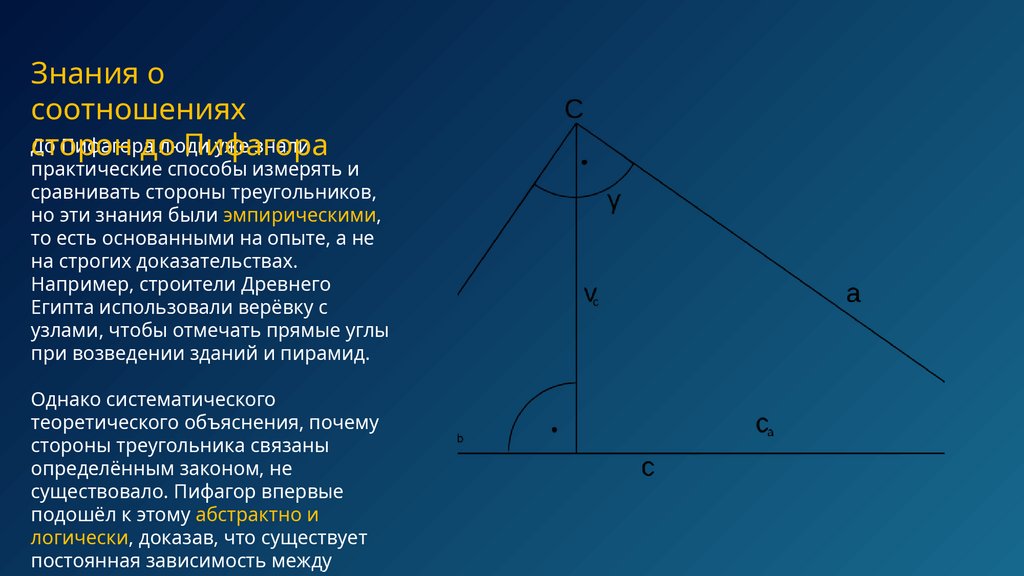
Знания о
соотношениях
До
Пифагора
люди
уже знали
сторон
до
Пифагора
практические способы измерять и
сравнивать стороны треугольников,
но эти знания были эмпирическими,
то есть основанными на опыте, а не
на строгих доказательствах.
Например, строители Древнего
Египта использовали верёвку с
узлами, чтобы отмечать прямые углы
при возведении зданий и пирамид.
Однако систематического
теоретического объяснения, почему
стороны треугольника связаны
определённым законом, не
существовало. Пифагор впервые
подошёл к этому абстрактно и
логически, доказав, что существует
постоянная зависимость между

19.

Пифагор и его школа внесли большой вклад в
Вклад
Пифагора
и его
развитие математики,
науки
и философии. Они
первыми начали рассматривать математику как
школы
науку, основанную на логике и доказательствах,
а не только на практических расчётах.
Пифагорейцы изучали числа, их свойства и
закономерности, открыли понятия чётных и
нечётных чисел, треугольных и совершенных
чисел, что стало основой для теории чисел.
Кроме математики, школа Пифагора развивала
астрономию, геометрию и музыку, показывая
связь чисел с гармонией мира. Их идеи о
порядке и пропорциях повлияли на философов и
учёных последующих поколений. Таким образом,
вклад Пифагора и его школы заключался не
только в открытии теоремы, но и в создании
целостного подхода к изучению природы через
числа и логику.

20.

Почему теорема названа
его именем
Теорема получила имя Пифагора,
потому что именно он и его школа
впервые систематически доказали
связь между сторонами
прямоугольного треугольника. Хотя
частично подобные знания
использовались и до него в
практических целях, Пифагор
подошёл к этому логически и
абстрактно, превратив наблюдение в
математический закон.
Кроме того, школа Пифагора
распространяла и сохраняла эти
знания, что закрепило его имя в
истории. Со временем его имя стало
символом этой фундаментальной
идеи, и именно поэтому теорема

21.

Доказательства
теоремы
• Идея первого
доказательств
доказательства
• а
Почему существует
много доказательств

22.

доказательств
Идея первого
доказательств
Первое
доказательство теоремы
а
Пифагора связано с геометрическим
подходом. Пифагор или его ученики
показали, что если построить квадрат
на каждой стороне прямоугольного
треугольника, то площадь квадрата
на гипотенузе будет точно равна
сумме площадей квадратов на
катетах.
Идея заключалась в разделении и
перекладывании фигур: квадраты на
катетах можно было разрезать на
части и переставить так, чтобы
полностью заполнить квадрат на
гипотенузе. Таким образом,
зависимость сторон треугольника
была показана наглядно и доказана

23.

Почему существует
Существует много доказательств теоремы
много
Пифагора, потому что эта теорема является
фундаментальной и универсальной — она
доказательств
используется во многих областях математики и
практических задачах. Разные подходы
показывают одну и ту же истину с разных сторон:
геометрически, алгебраически, с помощью
подобия фигур или даже через физические
модели.
Кроме того, математики на протяжении тысяч
лет искали новые, более простые или наглядные
способы объяснить теорему, чтобы её можно
было легче понимать и преподавать. Каждый
новый метод доказательства помогает лучше
понять связь сторон треугольника и развивает
логическое мышление.

24.

Применение
теоремы Пифагора
• В геометрии
• В реальной жизни
(строительство, техника)

25.

В геометрии
Теорема Пифагора широко
используется в геометрии для
вычисления длин сторон
прямоугольных треугольников. С её
помощью находят высоты,
диагонали, расстояния между
точками и размеры фигур.
Её применяют при решении задач на
площади и периметры, при
построении квадратов,
прямоугольников, треугольников, а
также для проверки, является ли
треугольник прямоугольным.
Теорема служит основой для
изучения более сложных
геометрических понятий, например,
подобия фигур, координатной

26.

В реальной жизни
(строительство,
техника)
Теорема Пифагора активно используется в
реальной жизни, особенно в строительстве и
технике. Например, строители с её помощью
вычисляют диагонали зданий, размеры
прямоугольных помещений и углы крыши,
чтобы всё было ровно и правильно.
В технике её применяют для расчёта расстояний
и перемещений, например, при проектировании
машин, мостов, подъёмных механизмов,
навигации и компьютерной графике. Теорема
помогает точно определять длины, углы и
пропорции там, где нужно соблюсти точность и
безопасность.