Geometricheskiy_smysl_proizvodnoy_povtorenie

1. Геометрический смысл производной

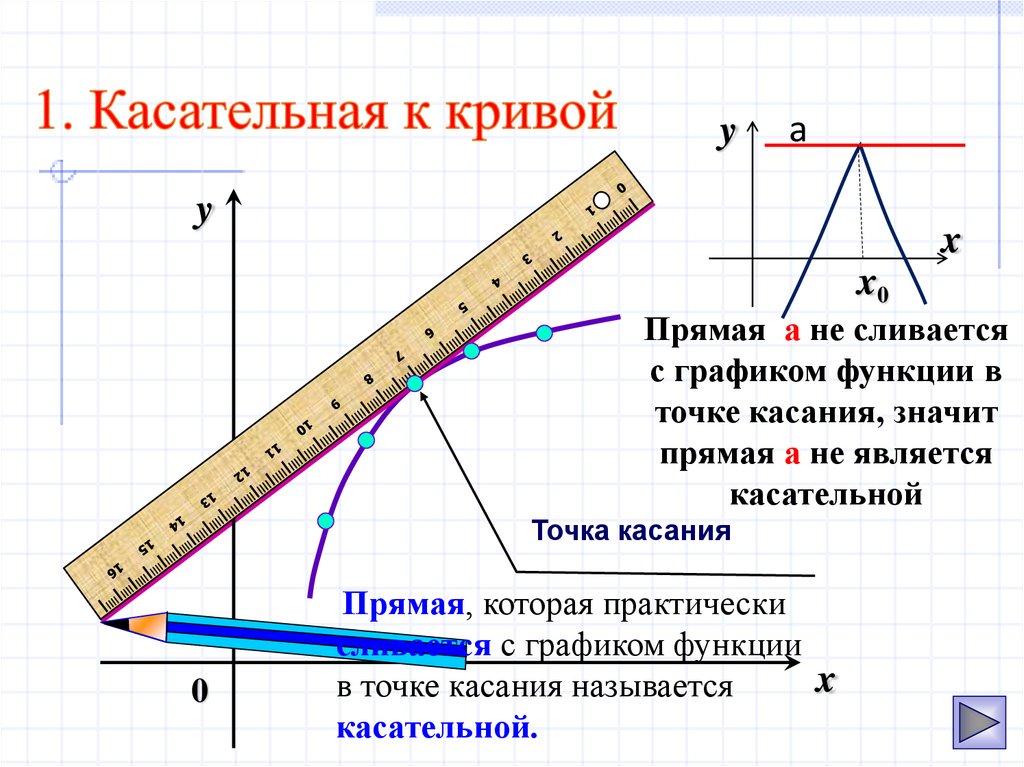
2. 1. Касательная к кривой

y
а
y
x
x0
Прямая а не сливается
с графиком функции в
точке касания, значит
прямая а не является
касательной
Точка касания
0
Прямая, которая практически
сливается с графиком функции
x
в точке касания называется
касательной.

3.

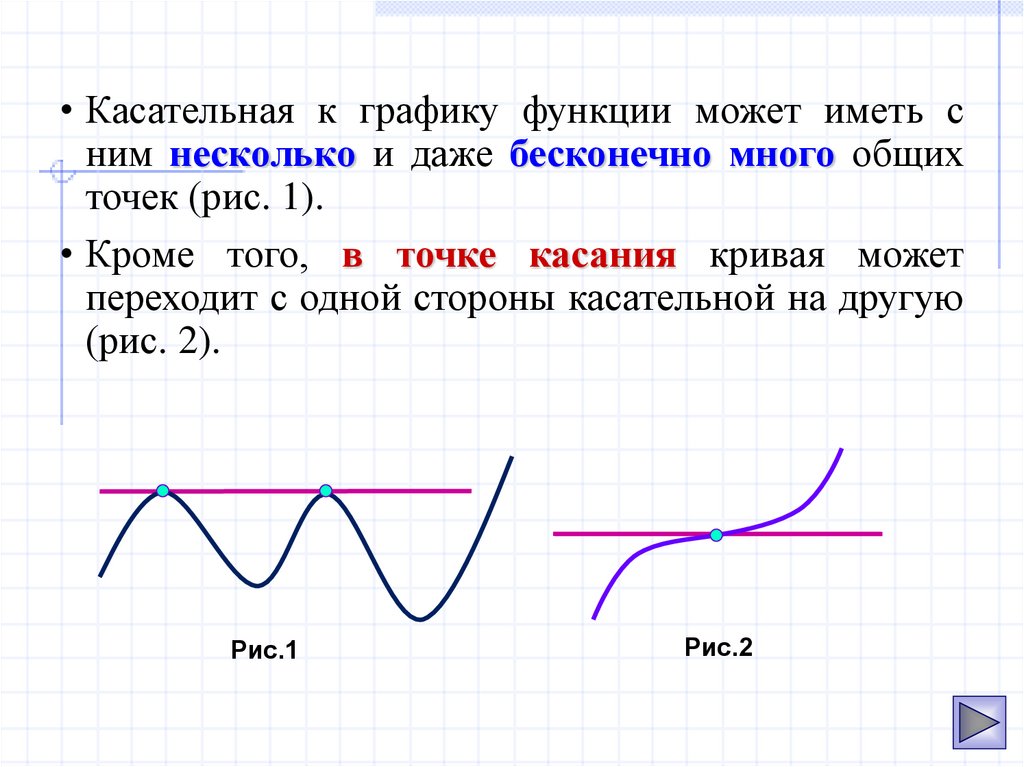
• Касательная к графику функции может иметь с
ним несколько и даже бесконечно много общих
точек (рис. 1).
• Кроме того, в точке касания кривая может
переходит с одной стороны касательной на другую
(рис. 2).
Рис.1
Рис.2

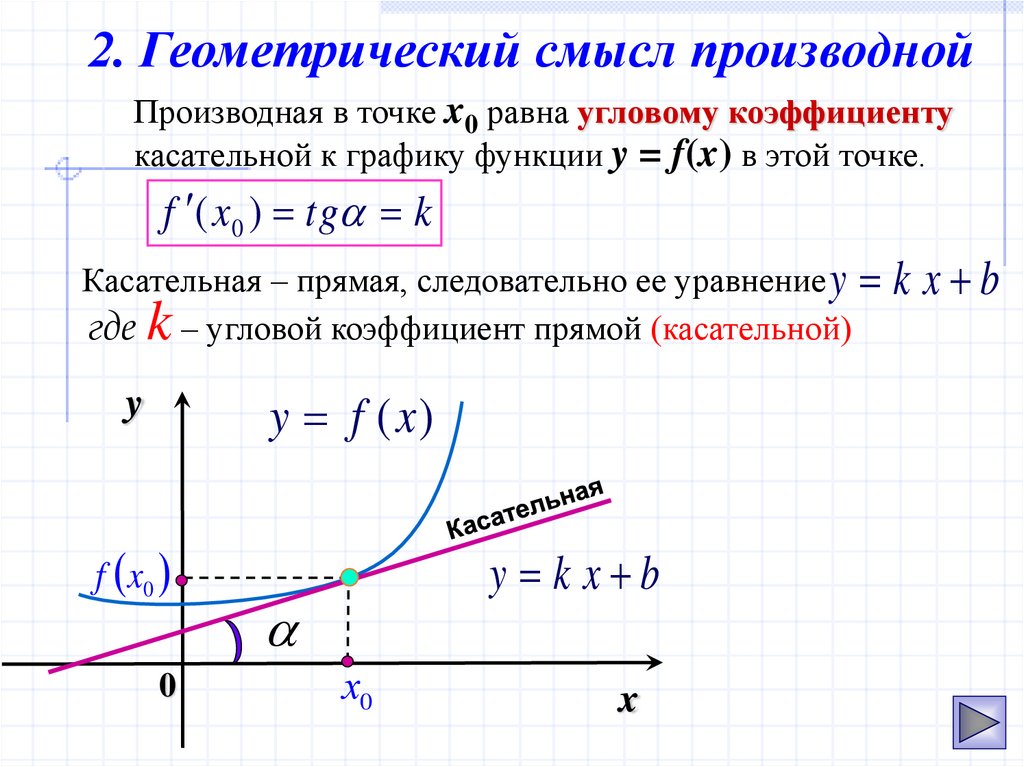
4. 2. Геометрический смысл производной

Производная в точке x0 равна угловому коэффициенту
касательной к графику функции y = f(x) в этой точке.
f ( x0 ) tg k
Касательная – прямая, следовательно ее уравнение y k x b
где – угловой коэффициент прямой (касательной)
k
y f (x )
y
f x0
0
y k x b
х0
x

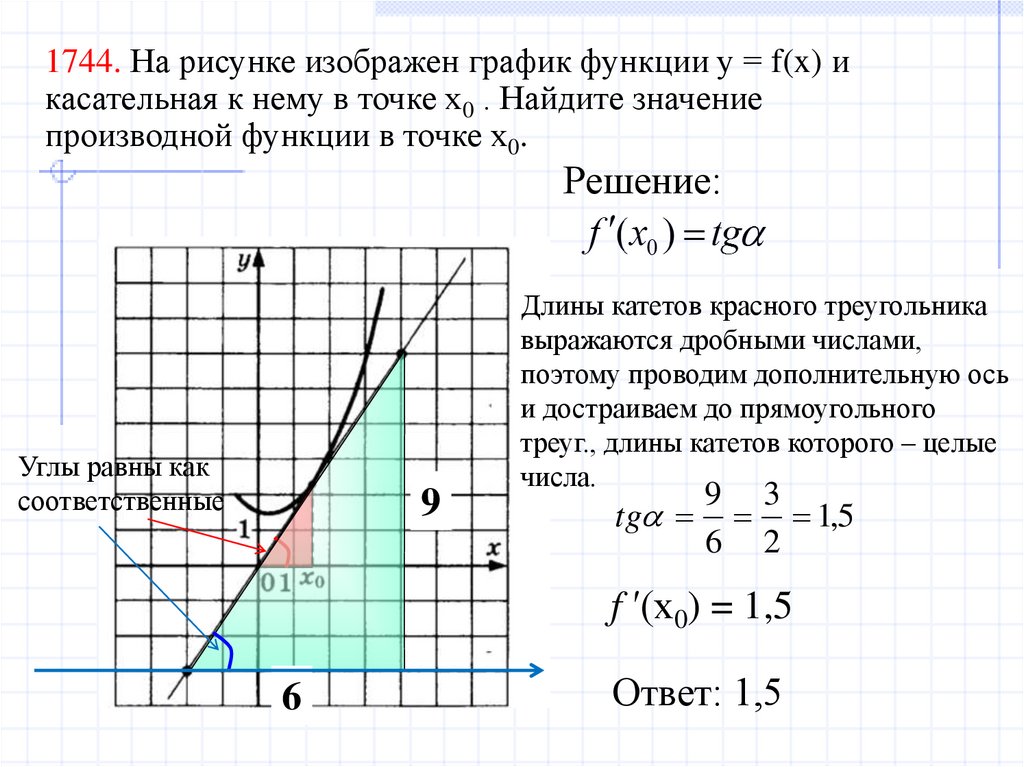
5. 1744. На рисунке изображен график функции у = f(x) и касательная к нему в точке х0 . Найдите значение производной функции в

точке х0.
Решение:
Углы равны как
соответственные
9
Длины катетов красного треугольника
выражаются дробными числами,
поэтому проводим дополнительную ось
и достраиваем до прямоугольного
треуг., длины катетов которого – целые
числа.
9 3
tg 1,5
6 2
f ′(x0) = 1,5
6
Ответ: 1,5

6. На рисунке изображен график функции у = f(x) и касательная к нему в точке х0 . Найдите значение производной функции в точке х0.

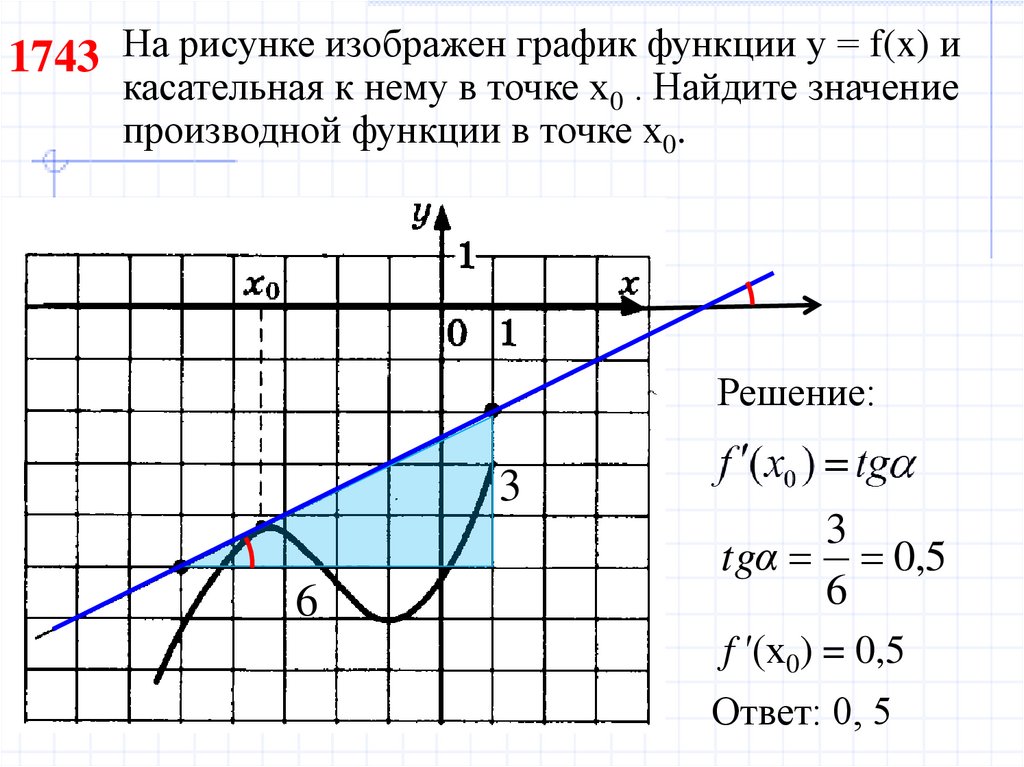
1743 На рисунке изображен график функции у = f(x) и
касательная к нему в точке х0 . Найдите значение
производной функции в точке х0.
Решение:
3
6
3
tgα 0,5
6
f ′(x0) = 0,5
Ответ: 0, 5

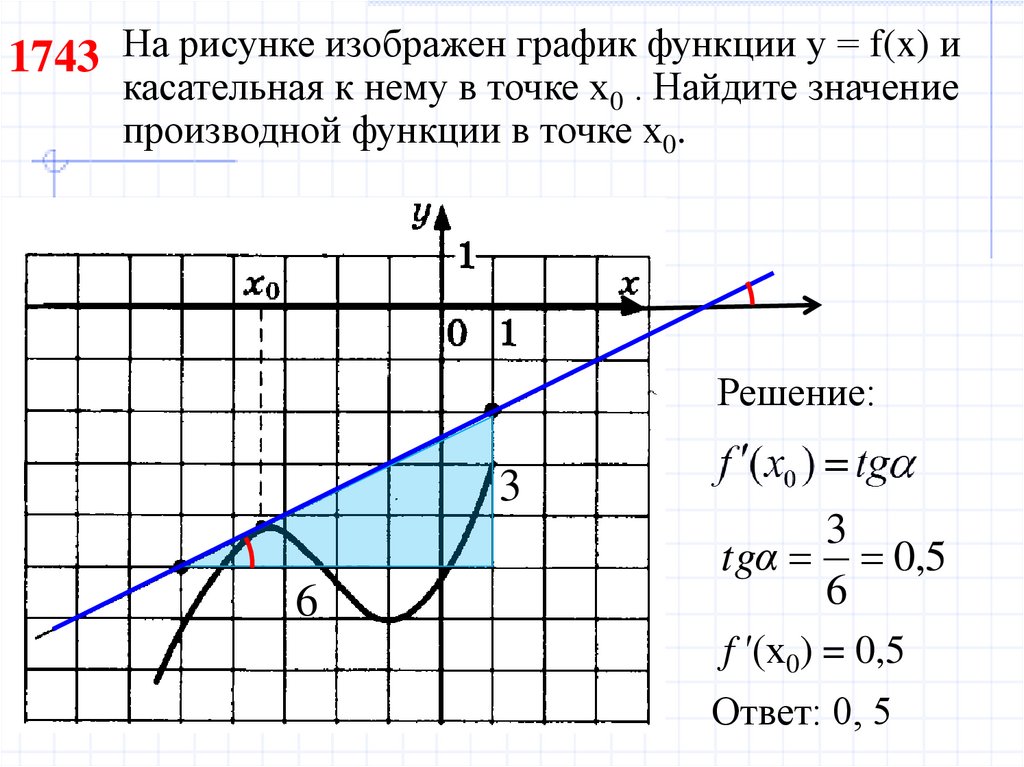
7. На рисунке изображен график функции у = f(x) и касательная к нему в точке х0 . Найдите значение производной функции в точке х0.

1743 На рисунке изображен график функции у = f(x) и
касательная к нему в точке х0 . Найдите значение
производной функции в точке х0.
Решение:
3
6
3
tgα 0,5
6
f ′(x0) = 0,5
Ответ: 0, 5

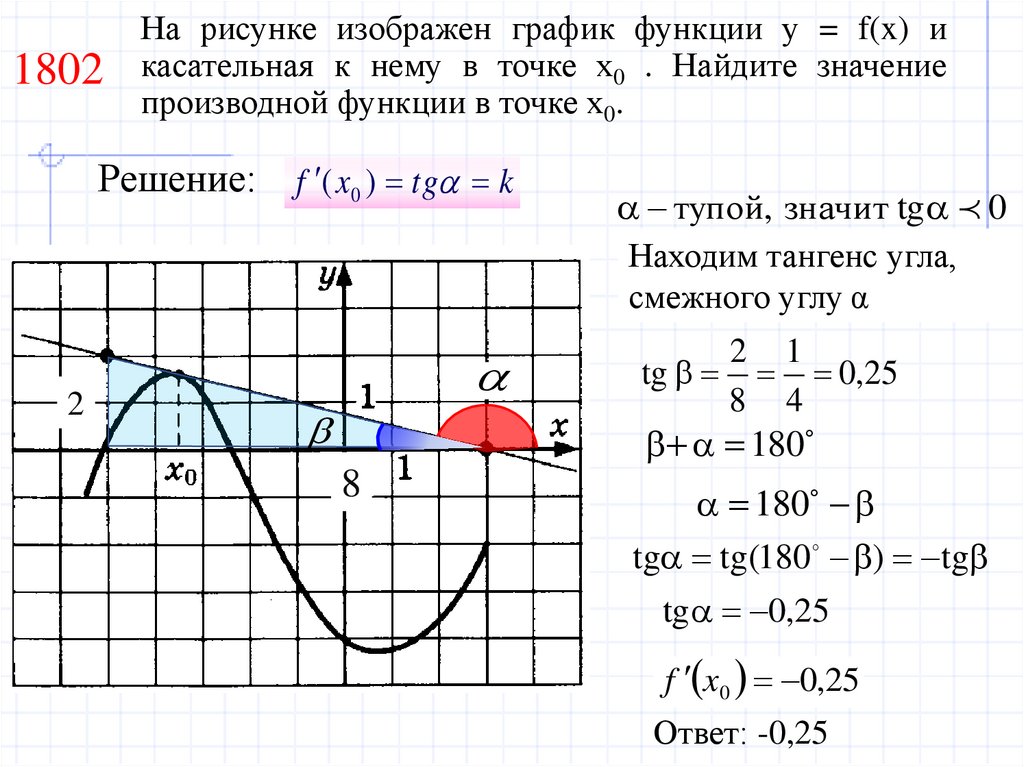
8. На рисунке изображен график функции у = f(x) и касательная к нему в точке х0 . Найдите значение производной функции в точке х0.

1802
На рисунке изображен график функции у = f(x) и
касательная к нему в точке х0 . Найдите значение
производной функции в точке х0.
Решение: f ( x0 ) tg k
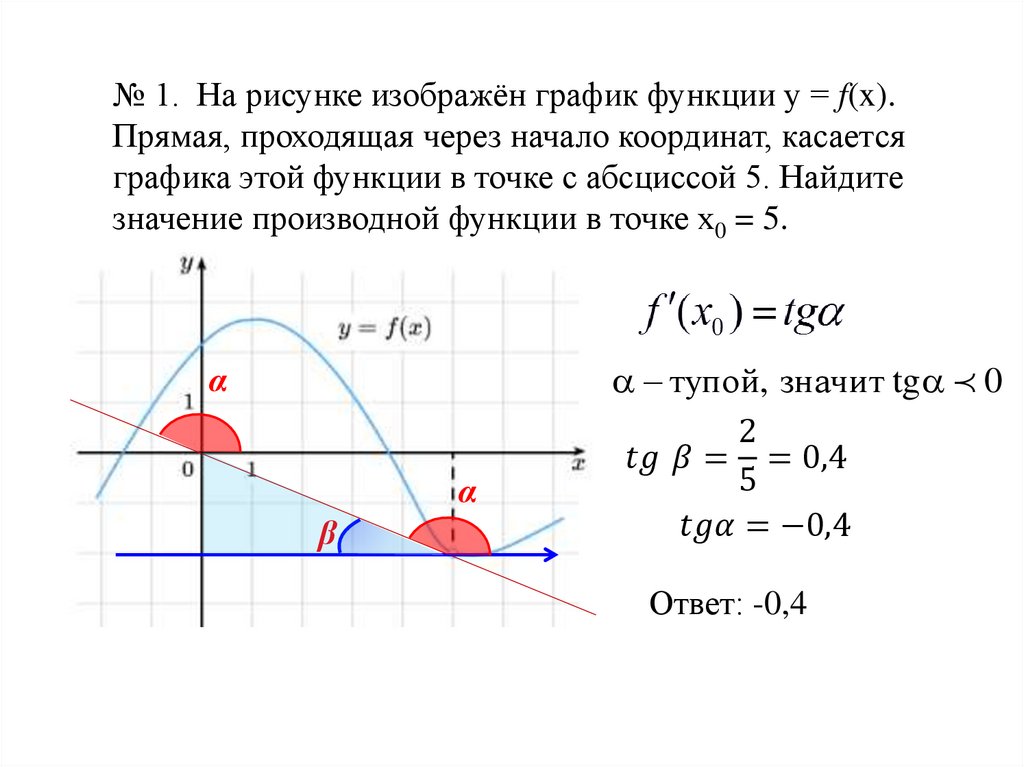
2
тупой, значит tg 0
Находим тангенс угла,
смежного углу α
2 1
tg 0,25
8 4
180
8
180
tg tg (180 ) tg
tg 0,25
f x0 0,25
Ответ: -0,25

9.

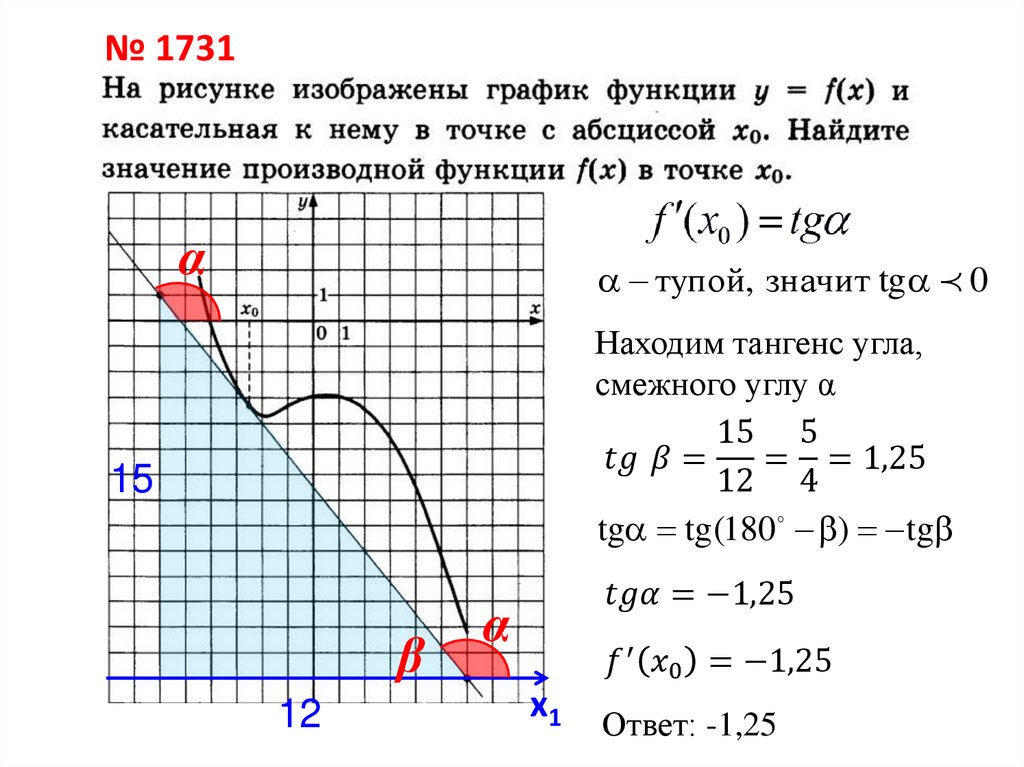
№ 1731
α
тупой, значит tg 0
Находим тангенс угла,
смежного углу α
15 5