Лекция 8(сгм) Интегрирование ФКП 25-26 (2)

1. Специальные главы математики

Лекция 7
Интегрирование функций
комплексной переменной

2.

Интеграл
2

3.

Интегрирование функций комплексной
переменной
Пусть L− гладкая ориентированная дуга на z-плоскости,
f(z)=u(x,y)+iv(x, y) − непрерывная функция, заданная на
дуге L.
Разобьем дугу L произвольным образом на n ячеек
(элементарных дуг) точками z1 , z2 ,..., zn (рис).
В этих ячейках выберем
произвольно точки
Составим сумму
где zk = |zk − zk−1|.
z0=
3

4.

Эта сумма называется интегральной суммой функции
f(z) по дуге L.
Найдем предел интегральной суммы при стремлении к
нулю величины
Если существует предел интегральной суммы
при d 0, не зависящий от способа разбиения дуги L и
выбора промежуточных точек
то
этот
предел
называется интегралом функции f(z) по дуге (L) и
обозначается
Для обозначения интеграла по замкнутому контуру
используется знак
4

5.

Свойства интеграла
1)
т.е. интеграл от функции комплексного переменного
определяется через два криволинейных интеграла
второго рода.
2) При изменении ориентации дуги интеграл
меняет знак.
3)
5

6.

4) Пусть | f(z)| M на дуге (L). Тогда,
где L − длина дуги.
5) Пусть z = z(t) − параметрическое уравнение дуги
AB, причем концам дуги A и B соответствуют значения
параметра tA и tB. Тогда
6

7.

Пример 1. Вычислить интеграл z Re z dz, если
L
а) L отрезок ОА; б) L отрезок AB; в) L отрезок BО;
г) L ломаная ОABО (см.рис.).
7

8.

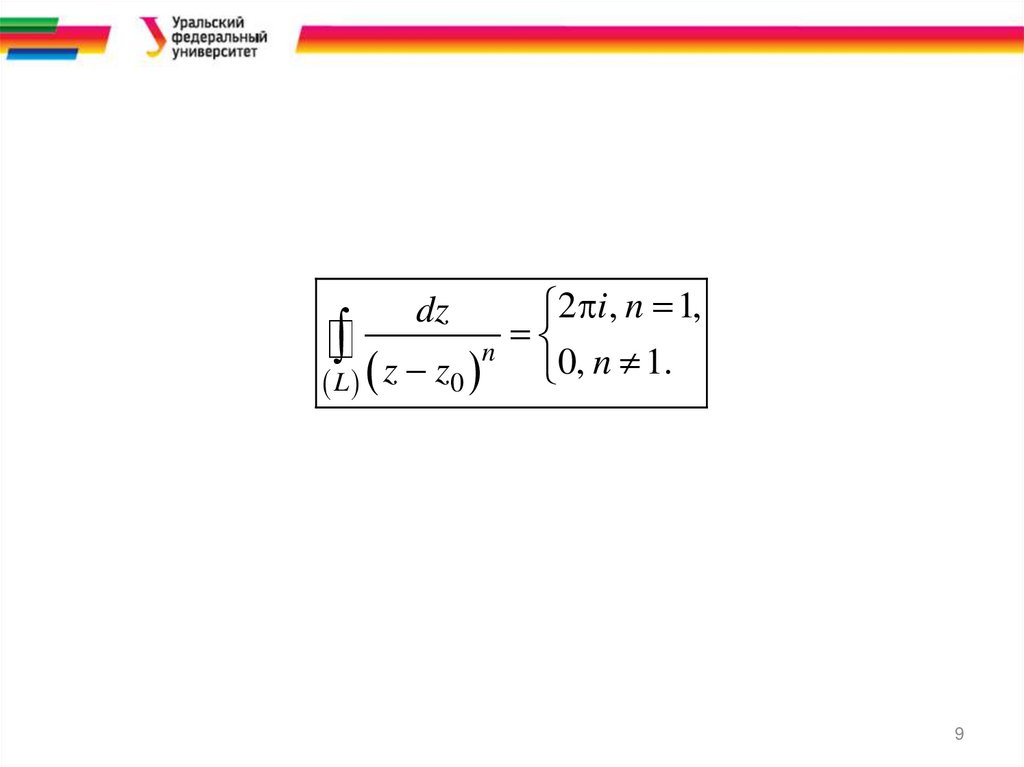
Пример 2. Вычислить интеграл
по окружности с центром в точке z0 радиуса R,
ориентированной против часовой стрелки.
8

9.

2 i, n 1,
z z n 0, n 1.
0
L
dz
9

10.

Пример 3. Вычислить
10

11.

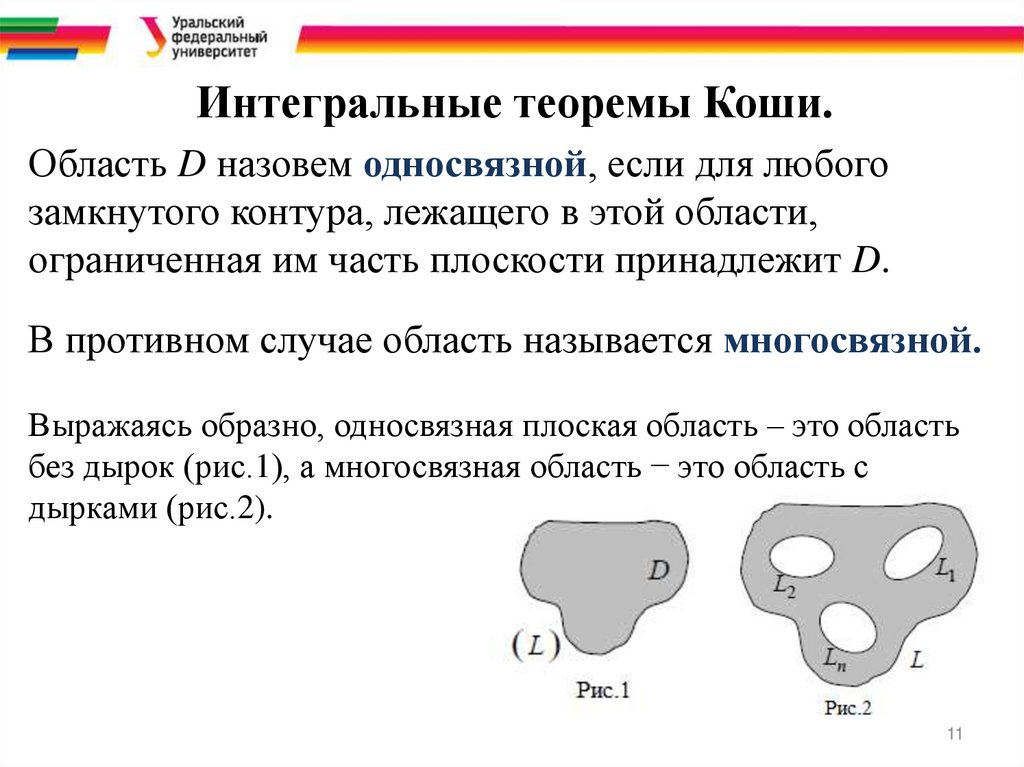
Интегральные теоремы Коши.
Область D назовем односвязной, если для любого
замкнутого контура, лежащего в этой области,
ограниченная им часть плоскости принадлежит D.
В противном случае область называется многосвязной.
Выражаясь образно, односвязная плоская область – это область
без дырок (рис.1), а многосвязная область − это область с
дырками (рис.2).
11

12.

Теорема Коши (для односвязной области).
Пусть D − односвязная плоская область и функция f(z)
является аналитической в области D и на ее границе (L).
Тогда
Доказательство. Рассмотрим интеграл
Так как контур (L) ограничивает односвязную область D, то к
каждому криволинейному интегралу можно применить
формулу Грина:
12

13.

Тогда f ( z ) dz v x u y dx dy i u x v y dx dy.
( L)
( D)
( D)
Функция f(z) является аналитической в области D,
поэтому ее действительная часть и мнимая часть
удовлетворяют условиям Коши-Римана:
u x = v y, u y = −v x,
вследствие чего подынтегральные функции в двойных
интегралах обращаются в нуль и
13

14.

Теорема Коши (для многосвязной области).
Пусть
1) D − многосвязная область, ограниченная внешним
контуром L и внутренними контурами L1, L2,…,Ln;
2) контуры L, L1, L2,…,Ln одинаково ориентированы (например,
против часовой стрелки);
3) функция f(z) является аналитической в области D и
непрерывной в замкнутой области D .
Тогда интеграл по внешнему контуру равен сумме интегралов
по внутреннему контуру:
14

15.

Доказательство.
Рассмотрим область, ограниченную внешним контуром L и
только одним внутренним контуром L1. Сделаем разрез по
линии AB (рис.3).
Обозначим через D −область D
c разрезом по линии AB.
Эта область будет односвязной
с границей L . По теореме Коши
для односвязной области
Но граница L состоит из линии L,
обходимой против часовой стрелки (обозначим ее L+),
линии AB; линии L1, обходимой по часовой стрелке (обозначим
ее L1 ), и линии BA.
15

16.

Поэтому
При изменении ориентации дуги интегралы меняют
знак, значит
поэтому
16

17.

Пример. Вычислить интеграл
по произвольной замкнутой линии, ориентированной
против часовой стрелки.
17

18.

Теорема (о первообразной).
Пусть функция f(z) непрерывна в односвязной области D и
по любому замкнутому контуру L из
области D. Тогда
1) интеграл
не зависит от формы кривой z0z,
обозначается
и является аналитической
функцией F(z) в области D;
2)
т.е. F(z) является
первообразной для f(z).
(без доказательства)
18

19.

Из этой теоремы следуют формула Ньютона-Лейбница
z
f ( )d F ( z ) F ( z0 ),
z0
где F(z) первообразная для f(z),
и формула интегрирования по частям
19

20.

Пример. Вычислить интеграл
по линии,
соединяющей точки z1 = 0, z2 = i.
20

21.

21

22.

22