6_Эвристические методы поиска

1. Эвристические процедуры поиска на графе

1

2. Недостатки методов слепого перебора

Методы
слепого
перебора
(неинформированные)
дают
решение
задачи, однако в процессе поиска для
нахождения
требуемого
решения
раскрывается слишком много вершин.
1) требуют много памяти;
2) низкое быстродействие.
Вследствие того, что на практике всегда
существует ограничения на время и память,
необходимо найти более эффективные
альтернативы
неинформированному
поиску.
2

3.

Для многих задач имеется возможность
использовать
некоторую
информацию,
относящуюся к рассматриваемой задаче, чтобы
содействовать сокращению поиска. Информацию
такого рода обычно называют эвристической, а
процедуры поиска, использующие ее – методом
эвристического поиска.
Эвристическую
информацию
можно
использовать для упорядочения вершин в списке
ОТКРЫТ на 9 этапе общей процедуры поиска на
произвольном графе в соответствии с их
«перспективностью», т.е. раскрывать в первую
очередь те вершины, которые в некотором смысле
ближе к целевой.
3

4. Понятие оценочной функции

В эвристических алгоритмах поиска используются оценочные
функции. Данная функция используется для упорядочения вершин в
списке ОТКРЫТ на 9 этапе общей процедуры поиска на
произвольном графе. При этом вершины в списке ОТКРЫТ
расположены в порядке возрастания соответствующих им значений
оценочной функции. Таким образом считается, что вершина, в
которой оценочная функция меньше, является более перспективной
для раскрытия и с большой вероятностью лежит на оптимальном
пути.
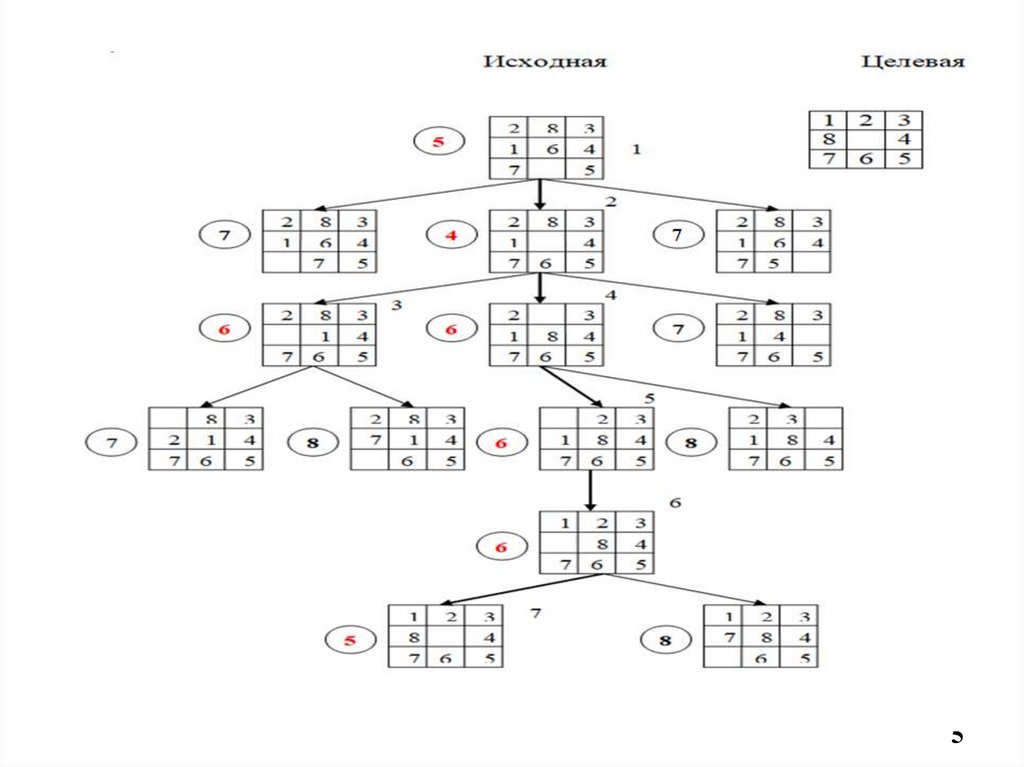
Пример: игра в 8.
Оценочная функция:
f(n) = d(n) + w(n),
где d(n) – глубина вершины n на дереве поиска,
w(n) - число находящихся не на своём месте клеток (фишек) в
описании состояния, связанном с вершиной n.
4

5.

5

6.

Значения оценочной функции f для каждой
вершины заключены в кружок, отдельно
выписанные числа указывают порядок, в
котором раскрываются вершины.
Найден тот же решающий путь, что и с
помощью других методов поиска, хотя
использование оценочной функции позволило
раскрыть значительно меньше вершин.
Если применить оценочную функцию,
равную f(n)=d(n) , то получаем процесс поиска
в ширину.
6