ЛОИС Лекция 11 2025 осень

1. Алгоритмы Лекция 11

§ 5. Меры нечеткости нечетких множеств.

2. § 5. Меры нечеткости нечетких множеств.

3. § 5. Меры нечеткости нечетких множеств.

4. § 5. Меры нечеткости нечетких множеств.

5. § 5. Меры нечеткости нечетких множеств.

6. § 5. Меры нечеткости нечетких множеств.

7. § 5. Меры нечеткости нечетких множеств.

8. § 5. Меры нечеткости нечетких множеств.

9. § 5. Меры нечеткости нечетких множеств.

10. § 5. Меры нечеткости нечетких множеств.

11. § 5. Меры нечеткости нечетких множеств.

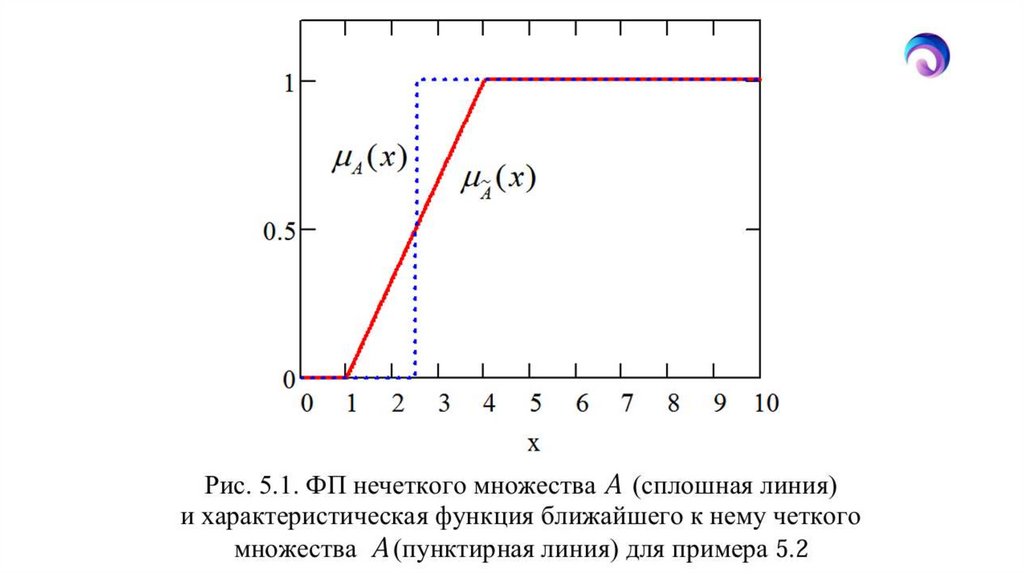
Пример 5.2. Нечеткое множество A задано своей функцией
принадлежности на универсальном множестве неотрицательных
действительных чисел:

12. § 5. Меры нечеткости нечетких множеств.

13.

14. § 5. Меры нечеткости нечетких множеств.

15. § 5. Меры нечеткости нечетких множеств.

16. § 5. Меры нечеткости нечетких множеств.

17. § 5. Меры нечеткости нечетких множеств.

18.

19. § 5. Меры нечеткости нечетких множеств.

20. § 5. Меры нечеткости нечетких множеств.

21. § 5. Меры нечеткости нечетких множеств.

22. § 5. Меры нечеткости нечетких множеств.

23.

24. § 5. Меры нечеткости нечетких множеств.

25. § 5. Меры нечеткости нечетких множеств.

26. § 5. Меры нечеткости нечетких множеств.

27. § 5. Меры нечеткости нечетких множеств.

28. § 5. Меры нечеткости нечетких множеств.

29. § 5. Меры нечеткости нечетких множеств.

Описанный выше подход оценки нечеткости множеств с помощью
индексов нечеткости, разумеется, не является единственно
возможным.
В частности, один из первых способов измерения степени
нечеткости был заимствован из физики.

30. § 5. Меры нечеткости нечетких множеств.

Известно, что мерой неупорядоченности физической системы
может служить энтропия.
Именно поэтому известны попытки приме нить энтропийный
подход и в теории нечетких множеств.
Однако выяснилось, что он обладает существенными
недостатками, а потому представляет скорее теоретический интерес.

31. § 5. Меры нечеткости нечетких множеств.

Более продуктивным оказался так называемый «аксиоматический
подход», который состоит в формулировании некоторого набора
аксиом, которым должна удовлетворять мера нечеткости F
множества.
Они могут быть, например, такими:

32. § 5. Меры нечеткости нечетких множеств.

33. § 5. Меры нечеткости нечетких множеств.

34. § 5. Меры нечеткости нечетких множеств.

Вопросы.
1. Что такое метрика? Сформулируйте аксиомы метрики.
2. Что такое четкое множество А, ближайшее к данному нечеткому
множеству A?
3. Как определяется индекс нечеткости НМ? Почему необходимо
учитывать мощность носителя?

35. § 5. Меры нечеткости нечетких множеств.

Задания.
Задание 1.

36. § 5. Меры нечеткости нечетких множеств.

Задания.
Задание 2.

37. § 5. Меры нечеткости нечетких множеств.

Задания.
Задание 3.