Uslubiy 1-topshiriq (2)

1.

OʻZBEKISTON RESPUBLIKASI
OLIY TA’LIM, FAN VA INNOVATSIYALAR
VAZIRLIGI
_______________________________________________
TOSHKENT MOLIYA INSTITUTI
“OLIY VA AMALIY MATEMATIKA”
KAFEDRASI
“MATEMATIKA” FANIDAN
USLUBIY KO‘RSATMA
(chiziqli algebraik tenglamalar sistemasi)
Toshkent – 2023

2.

3.

MUNDARIJA
_________________________________________________________
1
2
3
4
5
Matritsalar va ular ustida amallar .......................................................
Determinantlar nazariyasi ....................................................................
Matritsa rangi. Teskari matritsa ..........................................................
Vektorlar sistemasi va uning rangi .......................................................
Chiziqli algebraik tenglamalar sistemasi va uni yechishning Gauss
hamda Gauss-Jordan usullari ...............................................................
6 Chiziqli tenglamalar sistemasini yechishning matritsalar usuli va
Kramer qoidasi ......................................................................................
7 Bir jinsli chiziqli algebraik tenglamalar sistemasi. Fundamental
yechimlar sistemasi ................................................................................
Foydalanilgan adabiyotlar ro‘yxati ...................................................
3
4
24
36
49
62
82
95
105

4.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Agar siz matematikaning maftuni bo‘lmasangiz,
matematikada hech qanday yangilik yarata olmaysiz.
S.S.Soyer
MATRITSA VA ULAR USTIDA AMALLAR
_________________________________________________________
Ta’rif. Matritsa deb, m ta satr va n ta ustundan tashkil topgan
a11 a12 ... a1n
a 21 a22 ... a2 n
...
... ...
am1 am 2 ... amn
ko‘rinishidagi to‘g‘ri toʻrtburchakli sonlar jadvaliga aytiladi.
Matritsalar lotin alifbosining bosh harflari bilan belgilanadi. Masalan,
a11 a12 ... a1n
a 21 a22 ... a2 n
yoki
A=
...
... ...
am1 am 2 ... amn
Matritsani
tashkil
qilgan
A = (aij )
aij=
(i 1,=
m; j 1, n)
sonlar
matritsaning
elementlari, m × n matritsaning o‘lchovi deyiladi. Masalan,
2 −1 0
B = 4 8 9
−5 12 7
3 × 3 o‘lchovli matritsa
−1 2 7
A=
,
3 −5 4
2 × 3 o‘lchovli matritsa
Matritsaning turli ko‘rinishlari
1× n oʻlchovli A matritsaga satr matritsa
A = ( a11 a12 ... a1n )
yoki satr-vektor deyiladi.
m × 1 oʻlchovli A matritsaga ustun matritsa
yoki ustun-vektor deyiladi.
oʻlchovli A matritsaga
kvadrat matritsa deyiladi.
n×n
n -tartibli
4
a11
a21
A=
am1
a11 a12 ... a1n
a 21 a22 ... a2 n
A=
...
... ...
an1 an 2 ... ann

5.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Kvadrat
matritsada
a11 , a22 , ..., ann
elementlarning
tartiblangan
tо‘plamiga
matritsaning bosh (asosiy) diagonali deyiladi.
Agar A = (aij ) kvadrat matritsada i > j bo‘lib,
aij = 0 boʻlsa, A matritsa yuqori uchburchakli
matritsa deyiladi.
Agar A = (aij ) kvadrat matritsada i < j bo‘lib,
aij = 0 boʻlsa, A matritsa quyi uchburchakli
matritsa deyiladi.
Agar A = (aij ) kvadrat matritsada i ≠ j bo‘lib,
aij = 0 boʻlsa, A matritsa diagonal matritsa
deyiladi.
Agar A diagonal matritsaning barcha diagonal
elementlari oʻzaro teng boʻlsa, A matritsa
skalyar matritsa deyiladi.
a11 a12 ... a1n
0 a22 ... a2 n
A=
... ... ...
0 ... ann
0
0 ... 0
a11
a 21 a22 ... 0
A=
...
... ...
an1 an 2 ... ann
a11 0 ... 0
0 a22 ... 0
A=
... ... ...
0 ... ann
0
a 0 ... 0
0 a ... 0
A=
... ... ...
0 0 ... a
Agar A skalyar matritsada a = 1 boʻlsa, A
matritsa birlik matritsa deyiladi.
1
0
E =
...
0
0
1
...
0
...
...
...
0
0
...
1
Ixtiyoriy o‘lchovli matritsaning barcha
elementlari nol bo‘lsa, u holda bunday
matritsaga nol matritsa deyiladi.
0
0
Θ =
...
0
0
0
...
0
...
...
...
0
0
...
0
Matritsalar ustida amallar
Bir xil oʻlchovga ega matritsalar ustida algebraik qoʻshish amali bajariladi.
Bir xil oʻlchovga ega
a11 a12
a21 a22
...
...
A=
ai1 ai 2
...
...
a
m1 am 2
... a1 j
...
... a2 j
...
...
...
...
aij
...
...
... ...
... amj
...
...
a1n
b11 b12
a2 n
b21 b22
...
...
...
va B =
bi1 bi 2
ain
...
...
...
b
amn
m1 bm 2
5
... b1 j
... b2 j
...
...
...
bij
... ...
... bmj
... b1n
... b2 n
... ...
... bin
... ...
... bmn

6.

A.I.Sotvoldiyev, Sh.Sh.Omonov
matritsalarning yig‘indisi deb, ularning mos elementlari yigʻindisidan tuzilgan C
matritsaga aytiladi, ya’ni
a11 + b11 a12 + b12
a21 + b21 a22 + b22
...
...
C =
ai1 + bi1
ai 2 + bi 2
...
...
a +b
m1 m1 am 2 + bm 2
a1 j + b1 j
...
... a2 j + b2 j
...
...
...
...
aij + bij
...
...
...
...
... amj + bmj
...
...
...
a1n + b1n
a2 n + b2 n
...
.
ain + bin
...
amn + bmn
Izoh. Matritsalar ustida ayirish amali ham qo‘shish amali kabi amalga
oshiriladi.
m × n o‘lchovli A matritsani biror λ songa koʻpaytmasi deb, uning har bir
elementini shu songa koʻpaytirishdan tuzilgan C matritsaga aytiladi, ya’ni
a11 a12 ... a1 j ... a1n λ a11 λ a12 ... λ a1 j ... λ a1n
a21 a22 ... a2 j ... a2 n λ a21 λ a22 ... λ a2 j ... λ a2 n
...
... ... ... ... ... ...
...
... ... ...
...
.
C=
λ⋅
=
ai1 ai 2 ... aij ... ain λ ai1 λ ai 2 ... λ aij ... λ ain
...
... ... ...
...
... ... ... ... ... ...
...
a
m1 am 2 ... amj ... amn λ am1 λ am 2 ... λ amj ... λ amn
Misol. Ushbu
6 −2
1 3
va B =
A=
9 −1
−5 8
matritsalar berilgan bo‘lsa, −3 A + 2 B matritsani toping.
Yechish:
−3 ⋅ 3 −3 −9
1 3 −3 ⋅1
−3 A =−3 ⋅
=
=
,
−5 8 −3 ⋅ (−5) −3 ⋅ 8 15 −24
6 −2 2 ⋅ 6 2 ⋅ (−2) 12 −4
2B =
2⋅
=
2 ⋅ 9 2 ⋅ (−1) =
18 −2 ,
9
−
1
−3 −9 12 −4 −3 + 12 −9 + (−4) 9 −13
−3=
A + 2B
=
+ =
.
15 −24 18 −2 15 + 18 −24 + (−2) 33 −26
Izoh. Matritsalar ustida qoʻshish va ayirish, ya’ni algebraik qoʻshish hamda
songa koʻpaytirish amallari matritsalar ustida chiziqli amallar deyiladi.
Ta’rif. m × n o‘lchovli A matritsaning barcha satrlari mos ustunlari bilan
almashtirilsa, u holda hosil boʻlgan n × m o‘lchovli matritsaga transponirlangan
matritsa deyiladi va AT kabi belgilanadi.
6

7.

A.I.Sotvoldiyev, Sh.Sh.Omonov
a11 a12
a
a22
A = 21
...
...
am1 am 2
... a1n
... a2 n
... ...
... amn
⇒
a11
a
T
A = 12
...
a1n
a21
a22
...
a2 n
... am1
... am 2
... ...
... amn
2 −1
2 3 5
Masalan, A = 3 4 boʻlsa, AT =
boʻladi.
−
1
4
0
5 0
_________________________________________________________
1-NAZORAT TOPSHIRIQLARI
Quyidagi matritsalar ustida chiziqli amallarni bajaring.
1 −2 3
1. A 4 6 −1 ,
=
7 0 2
5 1 4
2. A 4 3 −1 ,
=
7 −2 1
6 5 2
3. A= −1 4 7 ,
3 1 0
2 −2 3
B = −3 1 4 ,
5 −3 9
3 0 8
B = −3 1 4 ,
5 −3 9
−2 1 7
B = 6 5 8 ,
2 −3 4
−1
2 ,
4
5 1 −2
B = −3 2 7 ,
4 0 −1
1 −2 −3
=
B 0 −3 1 ,
4 −4 5
8 −1 4
=
B 2 −3 5 ,
1 0 7
1 3
4. A= −2 5
0 1
1 −3
5. A = 0 2
3 −3
−2
6. A = 5
2
−1
7. A = 2
5
0
1 ,
2
3 1
4 4 ,
−1 −5
0 −6
1
1 4 , =
B 2
5
8 −9
−1 0 6
5
8. A 3 5 −2 ,
=
=
B 0
4 8 6
1
−1 4
7 −5 ,
4 8
7 1
4 −3 ,
2 8
7
2 A + 3B =
?
−4 A + 2 BT =
?
−5 AT + 4 B =
?
−2 A + BT =
?
4 A − 6 BT =
?
3 AT − 5 B =
?
−2 A + 7 B =
?
3 A − 2B =
?

8.

A.I.Sotvoldiyev, Sh.Sh.Omonov
−2 −3 −5
9. A = 0 1 4 ,
8 3 6
−1 2 −3
10. A= −4 5 1 ,
0 7 8
2 1 −5
11. A= −1 3 7 ,
1 4 2
3 −2 −3
12. A = 1 7 6 ,
5 −4 9
3 −2 1
13. A = 2 0 7 ,
6 5 4
−1 −2 4
14.
=
A 2 −5 1 ,
3 0 6
1 5
B= 7 9
−1 8
1 5
B = 3 1
8 −4
−5
B = 2
−2
1
B= 2
−5
−2
3 ,
4
?
−5 A + 6 B =
2
9 ,
1
AT − 2 B =
?
5 7
0 8 ,
−3 4
1 −3
7 6 ,
8 1
−1 2
=
B 5 −1
3 1
−1 −3
B = 3 0
4 2
−5 A + 2 BT =
?
4
0 ,
8
3 A + BT =
?
5
6 ,
7
−2 AT + 3B =
?
8 −5 1
15. A = 2 4 0 ,
3 −2 1
0 −4 1
16. A= −2 1 2 ,
3 −1 −3
3 1 2
B = −2 4 5 ,
1 −2 3
1 6 2
B = 2 1 3 ,
1 −3 1
2 −1 3
17. A = 1 4 2 ,
0 5 6
1 −1 −5
18. A = 4 3 6 ,
2 −2 7
2 −1 1
B = 2 4 5 ,
−3 5 3
1 1 5
B = −2 6 3 ,
2 5 −1
5 0 −4
19. A = 1 6 2 ,
1 3 −7
2 −1 3
B = 4 5 7 ,
6 2 0
8
2 AT + 3B =
?
3 A + 4B =
?
2 AT − 4 B =
?
−3 A + 5 B =
?
7 A − 2 BT =
?
−4 A + 5 BT =
?

9.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 −2 3
20. A= 4 −5 −1 ,
1 2 5
6 −1 4
21. A 5 2 −4 ,
=
7 1 3
1 −2 3
22. A 4 6 −1 ,
=
7 0 2
5 1 4
23. A 4 3 −1 ,
=
7 −2 1
−1 2 4
24.
=
A 3 −3 5 ,
6 2 1
5 2 2
25. A 4 1 −3 ,
=
7 −6 4
−2 2 3
26. A= −3 1 8 ,
5 2 1
3 −1
27. A = 5 1
7 −2
3 −1
28. A = 5 4
2 1
2
3 ,
4
−2
B= 5
6
−6
=
B 1
1
3 4
0 7 ,
1 −3
4 2
−5 8 ,
−3 7
2 −2 3
B = −3 1 4 ,
5 −3 9
3 0 8
B = −1 4 1 ,
5 −3 5
−1 5 3
=
B 4 −1 2 ,
0 7 6
4 −1 0
B = 7 1 3 ,
1 2 −1
4
B = 2
−1
−1
B = 1
2
−4 3
1 8 ,
2 5
2 −6
4 7 ,
5 1
2
−1 2 7
1 , =
B 6 5 −2 ,
3 −1 4
4
5 2 3
3 −2 1
29. A= −1 0 4 ,
B = 4 7 2 ,
7 2 1
1 5 −3
−4 1 6
9 1 −8
30.=
=
B 5 −3 2 ,
A 7 −5 2 ,
7 4 −5
1 3 4
9
− AT + BT =
?
3 AT + 2 B =
?
−2 AT + B =
?
AT + 3B =
?
3 A − 2 BT =
?
5 A − 4B =
?
2 AT + 4 B =
?
5 A − 2 BT =
?
6 AT − 7 B =
?
2 A + 7 BT =
?
7 AT − 4 B =
?

10.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Ta’rif. A matritsaning ustunlari soni B matritsaning satrlari soniga teng boʻlsa, A
matritsa B matritsa bilan zanjirlangan matritsa deyiladi.
Masalan,
−1 3 11
=
A 4 9 −6
2 −2 7
1 7
va B = 2 8
5 −1
matritsalar zanjirlangan matritsalar boʻladi. Chunki, A matritsaning ustunlari soni
3 ga, B matritsaning satrlari soni ham 3 ga teng bo‘lib, ular oʻzaro teng.
Izoh. Faqat va faqat zanjirlangan matritsalar ustida koʻpaytirish amali
bajariladi.
Am×n = (aik ) matritsani Bn× p = (bkj ) matritsaga koʻpaytmasi deb, Сm× p = (cij )
matritsaga aytiladi. Bunda
c=
ai1b1 j + ai 2b2 j + ... + aik bkj
ij
Bundan ko‘rinadiki, C matritsadagi cij element A matritsaning i -satrida
joylashgan har bir elementni B matritsaning j -ustunida joylashgan mos oʻrindagi
elementga koʻpaytirish va hosil boʻlgan koʻpaytmalarni qoʻshish natijasida
aniqlanadi. Masalan,
a11 a12
b
b
A = a21 a22 va B = 11 12
b21 b22
a
a
31 32
koʻrinishdagi matritsalar berilgan
quyidagicha amalga oshiriladi:
a11
AB =
a21
a31
boʻlsin.
Bu
a12
a11b11 + a12b21
b11 b12
a22 ⋅
a b +a b
=
b21 b22 21 11 22 21
a32
a31b11 + a32b21
matritsalarni
koʻpaytirish
a11b12 + a12b22
a21b12 + a22b22 .
a31b12 + a32b22
Misol. Ushbu
1 3 2
−2 1
va B 4 3
=
=
A 0 4 −1
0 5
5 1 −3
matritsalar berilgan bo‘lsa, A va B matritsalarning ko‘paytmasini toping.
Yechish:
1 ⋅1 + 3 ⋅ 3 + 2 ⋅ 5
1 3 2 −2 1 1 ⋅ (−2) + 3 ⋅ 4 + 2 ⋅ 0
AB= 0 4 −1 ⋅ 4 3 = 0 ⋅ (−2) + 4 ⋅ 4 + (−1) ⋅ 0 0 ⋅1 + 4 ⋅ 3 + (−1) ⋅ 5 =
5 1 −3 0 5 5 ⋅ (−2) + 1 ⋅ 4 + (−3) ⋅ 0 5 ⋅1 + 1 ⋅ 3 + (−3) ⋅ 5
10
10 20
16
7
−6 −7

11.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Eslatma. Agar A va B bir xil tartibli kvadrat matritsalar boʻlsa, har doim
AB va BA koʻpaytmalarini topish mumkin.
A kvadrat matritsani k (k ∈ N ) darajaga ko‘tarish: Ak =
A ⋅
A
⋅ ... ⋅
A kabi
k marta
amalga oshiriladi.
_________________________________________________________
2-NAZORAT TOPSHIRIQLARI
Quyidagi matritsalarning ko‘paytmasini toping.
1.
3 −2 3 4
⋅
,
−
5
4
2
5
2.
2 −3 9 −6
⋅
,
4 −6 6 −4
3.
2 5 −2 3
⋅
,
1 3 3 −5
4.
1 2 5 6
⋅
,
3
4
6
8
5.
1 2 −4 2
⋅
,
8 3 5 0
6.
1 2 4 1
−
⋅
,
4 8 1 2
7.
1 −1 −3 0
⋅
,
2 5 4 1
8.
2 3 0 1
⋅
,
8 −1 2 3
9.
2 5 3 −7
1 0 ⋅ 1 4 ,
1 0
0 1 ,
2 0
5 6
2 5 ,
3 2
1 1 1
1 2 3
⋅ 1 2 4
4 5 6 1 3 9
1 2
2 1 −1
0 3 5 ⋅ 1 −2
1 3
1
3
0
1
3
2
2 1 2
4 0 ⋅ −3
2 1 1
−3 2 2
−4 1 ⋅ 1
−5 3 1
5
6
4
1
5
3
8 −4 3 9 5
9 −5 ⋅ 4 −1 3 ,
7 −3 9 6 5
4 3 2 −1 5
−1 −1 ⋅ 1 4 −1 ,
6 7 3 −5 2
3 0 1 1 0
1 −2 −1 ⋅ 5 1
2 0 1 2 −3
2 −1
1 2 1
⋅ 1 3
3 1 2 0 1
4
0
5
2
0
4
2 6 0
1 2 ⋅ 2
7 3 1
7 5 1
1 3 ⋅ 7
2 8 2
3 8
1 7 ,
3 5
5 3
9 11 ,
1 0
1 1 1
1 2 3
⋅ 1 2 1
4 0 1 −1 1 0
0 3
1 2 −1
⋅ −1 2
3 0 1 1 −2
5
2
1
1
8
0
3 0 4
1 7 ⋅ 2
3 5 5
0 8 4
1 0 ⋅ 3
1 8 2
2 3
1 0 ,
6 7
2 3
2 4 ,
4 3
1 2
1 −2 ⋅ 2 1 −1
1 3 0 0 −5
1 3
1 2 −1
0 −2 ⋅ 3 0 1
−1 2
2 7 2 1 0 1
1 1 3 ⋅ 2 1 3 ,
5 6 7 3 2 0
1 2 0
1 2 −1
⋅ 1 2 1
0 3 4 1 2 3
11

12.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 2 −3 4
10.
⋅
,
0 7 5 8
1 2 4 3
11.
⋅
,
0
3
2
1
2 1 −1 2
,
5
12.
⋅
0 3 3
−1 0 2 5
13.
⋅
,
4 3 7 1
−2 0 2 5
14.
⋅
,
4 1 3 1
2 7 1 1
15.
⋅
,
0
3
3
4
2 −3 2 0
16.
⋅
,
4 5 3 1
3 4 3 −2
17.
⋅
,
2 5 5 −4
9 −6 2 −3
18.
⋅
,
6 −4 4 −6
−2
19.
3
3 2 5
,
⋅
−5 1 3
5 6 1 2
20.
⋅
,
7 8 3 4
1 5 8 8 0 1
7 3 1 ⋅ 3 2 5 ,
2 4 0 1 1 1
0 2 −1 4 3 2
−2 −1 2 ⋅ 3 2 1 ,
3 −2 −1 1 3 5
1 2 2 4 1 1
2 1 2 ⋅ −4 2 0 ,
1 2 3 1 2 0
1 −2 −1 −2 2 −3
3 1 2 ⋅ −4 3 −5 ,
1 2 2 5 −4 7
−2 2 −3 1 −2 −1
−4 3 −5 ⋅ 3 1 2 ,
5 −4 7 1 2 2
4 1 1 1 2 2
−
4 2 0 ⋅ 1 1 2 ,
1 2 1 1 2 3
1
5
10
1
−
1
3
1 1 −11 −4 1
4 3 ⋅ −25 9 −2 ,
5 1 15 −5 1
2 3 4 1 2
1 2 ⋅ 0 −1 1 ,
2 −1 1 2 1
2
1
0
1
0
2
−1
1 2 1
3 ⋅
3 1 2
1
2
1 2 −1
3 ⋅
1 3 0
4
5
−
3
(1 −2 3 0 ) ⋅
−4
1
−4
2 0 3
−
⋅ −3
1 2 1 5
2
3 5 −1
2 −2 0 ⋅ −3
5
−2
−3 2 0
−2 5 −1 ⋅ 0
3
4
0
1
4
2
−1
1 2 0
(1 4 −2 ) ⋅ 3 5 7
4 1 2
2 3 −2 1 0
3 1 1 ⋅ 2 −1
1 5 −5 0 1
1 3 2 2 2 3
−
3 2 0 ⋅ 0 1 4 ,
4 −3 5 −1 1 0
1 0 1 2 2 0
2 −1 0 ⋅ −1 0 1 ,
3 2 5 3 2 7
1 3
1 1 −1
⋅ 2 −1
0 1 2 0 1
1 5
−
⋅ 1 2 3
1
0
2 1 −1 0 2
0 1 2 2 1 5
−1 −2 3 ⋅ 0 1 0 ,
4 0 1 2 −1 −1
2 1
⋅ 2 1 5
−
3
1
0 1 −2 3 1
12

13.

A.I.Sotvoldiyev, Sh.Sh.Omonov
−4 2 1 2
21.
⋅
,
5 0 8 3
4 1 1
2
22.
⋅ −
,
1
2
4
8
−3 0 1 −1
23.
⋅
,
4 1 2 5
0 1 2
3
24.
⋅
,
2 3 8 −1
3 −4 2 5
25.
⋅
,
1
4
1
0
−3 4 1 2
⋅
,
8 0 7
26.
5
4 3 1 2
27.
⋅
,
2 1 3 −4
−1 2 2 1
,
⋅
5 0 3
28.
3
2 5 −1 0
29.
⋅
,
7 1 4 3
2 5 −2 0
30.
⋅
,
3 1 4 1
2
1
2
2
1
4
1 4 1
3 4 ⋅ 2
7 4 4
4 7 0
3 0 ⋅ 4
5 6 1
3 3
1 1 ,
0 0
3 2
5 0 ,
2 1
2 1 3 1
1 1 0 ⋅ 1
−1 1 1 2
1 −1
1 −1 0
2 1 1 ⋅ 1 0
0 1
3
1
2
3
4
3
4 5 4
0 1 ⋅ 1
3 1 3
5 1 4
1 2 ⋅ 5
2 4 1
7 1
0 2 ,
1 0
1 2
0 8 ,
3 0
1 0 1
1 1 1
1 2 1 ⋅ 1 1 0
0 1 1
1 3
2 3 0
⋅ 0 1
0 1 −1 3 −1
1
2
7
4
3
0
2 3 4 7 1
0 4 ⋅ 0 6 0 ,
8 9 2 0 3
7 2 1 −6 7
8 3 ⋅ −2 0 −4 ,
1 2 3 1 0
2 1 1 2 1
1 0 1 ⋅ 1 0
1 1 1 1 1
3
1 0 −4
⋅ −1
−1 5 1 6
3
1
7
3
5
4
2 4 4 3 1
3 5 ⋅ 1 0 2 ,
8 3 −3 1 0
2 1 4 2 1
−7 3 ⋅ 0 1 3 ,
5 −6 1 −4 0
5 1
−
⋅ 1 −1 2
1
2
0 1 3 1 0
2 3
4 1 ⋅ 1 −1 1
5 1 0 1 0
3 −8 1 3
4 5 7 ⋅ 2
1 2 0 1
4 −5 1 1
⋅
3
8
4
0
1 −3 1 3
13
4 1
5 2 ,
7 0
1 2
2 1 ,
3 0
−1 1
⋅ 2 4
3
0
1 −2 7 1
2 1
2 1
−
⋅ 1 2
1 2 1 1

14.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Matritsani iqtisodiy xarakterga oid masalalarda qo‘llanilishiga misol va
masalalar:
Misol. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
2 3
A = 5 2 matritsa, mahsulot ishlab
1 4
foydalanadi. Xomashyo xarajatlari –
chiqarish rejasi – C = (100 80 130 ) satr-matritsa, har bir xomashyo turining bir
30
ustun-matritsa koʻrinishida berilgan bo‘lsin.
50
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
Yechish: Bu masalani 2-xil usulda ko‘rib chiqamiz:
1-usul. Har bir xomashyo sarfini aniqlaymiz:
2 3
S = C ⋅ A = (100 80 130 ) ⋅ 5 2 = ( 730 980 ) .
1 4
Endi esa xomashyoning umumiy bahosini topamiz:
30
Q = S ⋅ B = ( 730 980 ) ⋅ = ( 70900 ) .
50
2-usul. Avval har bir mahsulot turiga sarflanuvchi xomashyo miqdorini
aniqlaymiz:
2 3
210
30
R = A ⋅ B = 5 2 ⋅ = 250 .
1 4 50 230
Endi esa xomashyoning umumiy bahosini topamiz:
210
Q = C ⋅ R = (100 80 130 ) ⋅ 250 = ( 70900 ) .
230
Demak, har ikki usulda ham mahsulotning umumiy bahosi bir hil ekan.
_________________________________________________________
14

15.

A.I.Sotvoldiyev, Sh.Sh.Omonov
3-NAZORAT TOPSHIRIQLARI
Quyidagi iqtisodiy mazmundagi masalalarni yeching.
1. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
1 5
A = 3 2
4 1
foydalanadi. Xomashyo harajatlari –
matritsa, mahsulot ishlab
chiqarish rejasi – C = (100 120 140 ) satr-matritsa, har bir xomashyo turining bir
40
ustun-matritsa koʻrinishida berilgan bo‘lsin.
70
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
2. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
1 4 2
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
7 5 3
chiqarish rejasi – C = ( 80 150 ) satr-matritsa, har bir xomashyo turining bir birligi
15
bahosi (pul.birl.) – B = 20 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
30
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
3. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
3 1
A = 2 4
5 3
foydalanadi. Xomashyo harajatlari –
matritsa, mahsulot ishlab
chiqarish rejasi – C = ( 200 230 250 ) satr-matritsa, har bir xomashyo turining bir
50
ustun-matritsa koʻrinishida berilgan bo‘lsin.
90
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
4. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
1 2 4
foydalanadi. Xomashyo harajatlari – A = 5 1 6 matritsa, mahsulot ishlab
2 3 5
15

16.

A.I.Sotvoldiyev, Sh.Sh.Omonov
chiqarish rejasi – C = (120 160 180 ) satr-matritsa, har bir xomashyo turining bir
10
birligi bahosi (pul.birl.) – B = 30 ustun-matritsa koʻrinishida berilgan bo‘lsin.
50
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
5. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 1 5
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
2 3 2
chiqarish rejasi – C = (100 70 ) satr-matritsa, har bir xomashyo turining bir birligi
20
bahosi (pul.birl.) – B = 30 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
40
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
6. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
1 1
A = 3 4
2 5
foydalanadi. Xomashyo harajatlari –
matritsa, mahsulot ishlab
chiqarish rejasi – C = (100 200 300 ) satr-matritsa, har bir xomashyo turining bir
80
ustun-matritsa koʻrinishida berilgan bo‘lsin.
100
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
7. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
2 0 5
foydalanadi. Xomashyo harajatlari – A = 3 1 4 matritsa, mahsulot ishlab
1 5 2
chiqarish rejasi – C = (100 150 200 ) satr-matritsa, har bir xomashyo turining bir
45
birligi bahosi (pul.birl.) – B = 70 ustun-matritsa koʻrinishida berilgan bo‘lsin.
95
16

17.

A.I.Sotvoldiyev, Sh.Sh.Omonov
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
8. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
4 1
A = 0 3 matritsa, mahsulot ishlab
2 5
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = ( 70 120 90 ) satr-matritsa, har bir xomashyo turining bir
50
ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
9. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
1 2 5
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
2 4 6
chiqarish rejasi – C = ( 55 80 ) satr-matritsa, har bir xomashyo turining bir birligi
40
bahosi (pul.birl.) – B = 60 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
80
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
10. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
1 4 2
foydalanadi. Xomashyo harajatlari – A = 5 1 3 matritsa, mahsulot ishlab
2 1 7
chiqarish rejasi – C = (110 125 155 ) satr-matritsa, har bir xomashyo turining bir
20
birligi bahosi (pul.birl.) – B = 45 ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
17

18.

A.I.Sotvoldiyev, Sh.Sh.Omonov
11. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
2 1
A = 4 7
5 9
foydalanadi. Xomashyo harajatlari –
matritsa, mahsulot ishlab
chiqarish rejasi – C = ( 65 80 95 ) satr-matritsa, har bir xomashyo turining bir
30
ustun-matritsa koʻrinishida berilgan bo‘lsin.
60
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
12. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 3 1
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
6 7 8
chiqarish rejasi – C = ( 60 100 ) satr-matritsa, har bir xomashyo turining bir birligi
10
bahosi (pul.birl.) – B = 20 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
40
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
13. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
1 5
A = 4 8 matritsa, mahsulot ishlab
2 1
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = ( 70 80 120 ) satr-matritsa, har bir xomashyo turining bir
70
ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
14. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
2 3 4
foydalanadi. Xomashyo harajatlari – A = 5 6 7 matritsa, mahsulot ishlab
8 9 1
chiqarish rejasi – C = ( 90 100 110 ) satr-matritsa, har bir xomashyo turining bir
18

19.

A.I.Sotvoldiyev, Sh.Sh.Omonov
20
birligi bahosi (pul.birl.) – B = 25 ustun-matritsa koʻrinishida berilgan bo‘lsin.
30
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
15. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
3 1 9
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
7
2
5
chiqarish rejasi – C = ( 200 300 ) satr-matritsa, har bir xomashyo turining bir
35
birligi bahosi (pul.birl.) – B = 55 ustun-matritsa koʻrinishida berilgan bo‘lsin.
65
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
16. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
4 1
A = 3 7
9 2
foydalanadi. Xomashyo harajatlari –
matritsa, mahsulot ishlab
chiqarish rejasi – C = (10 20 30 ) satr-matritsa, har bir xomashyo turining bir
50
ustun-matritsa koʻrinishida berilgan bo‘lsin.
40
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
17. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 2 7
foydalanadi. Xomashyo harajatlari – A = 1 6 3 matritsa, mahsulot ishlab
5 9 1
chiqarish rejasi – C = (170 180 190 ) satr-matritsa, har bir xomashyo turining bir
30
birligi bahosi (pul.birl.) – B = 55 ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
19

20.

A.I.Sotvoldiyev, Sh.Sh.Omonov
18. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
1 6
A = 9 2 matritsa, mahsulot ishlab
3 5
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = ( 60 50 40 ) satr-matritsa, har bir xomashyo turining bir
10
ustun-matritsa koʻrinishida berilgan bo‘lsin.
15
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
19. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
6 2 7
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
1 4 9
chiqarish rejasi – C = ( 80 85 ) satr-matritsa, har bir xomashyo turining bir birligi
35
bahosi (pul.birl.) – B = 40 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
45
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
20. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
6 1 5
foydalanadi. Xomashyo harajatlari – A = 3 2 7 matritsa, mahsulot ishlab
4 8 9
chiqarish rejasi – C = ( 90 110 130 ) satr-matritsa, har bir xomashyo turining bir
40
birligi bahosi (pul.birl.) – B = 75 ustun-matritsa koʻrinishida berilgan bo‘lsin.
100
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
21. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
2 1
A = 4 6 matritsa, mahsulot ishlab
5 8
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = ( 20 80 140 ) satr-matritsa, har bir xomashyo turining bir
20

21.

A.I.Sotvoldiyev, Sh.Sh.Omonov
30
ustun-matritsa koʻrinishida berilgan bo‘lsin.
70
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
22. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
6 9 12
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
1
5
10
chiqarish rejasi – C = ( 60 90 ) satr-matritsa, har bir xomashyo turining bir birligi
30
bahosi (pul.birl.) – B = 60 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
90
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
23. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
foydalanadi. Xomashyo harajatlari –
5 11
A = 2 1 matritsa, mahsulot ishlab
7 4
chiqarish rejasi – C = (100 120 140 ) satr-matritsa, har bir xomashyo turining bir
40
ustun-matritsa koʻrinishida berilgan bo‘lsin.
80
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
24. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 1 8
foydalanadi. Xomashyo harajatlari – A = 6 5 3 matritsa, mahsulot ishlab
10 2 7
chiqarish rejasi – C = (150 100 50 ) satr-matritsa, har bir xomashyo turining bir
15
birligi bahosi (pul.birl.) – B = 35 ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
21

22.

A.I.Sotvoldiyev, Sh.Sh.Omonov
25. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 10 3
matritsa, mahsulot ishlab
9 2
foydalanadi. Xomashyo harajatlari – A =
5
chiqarish rejasi – C = ( 70 120 ) satr-matritsa, har bir xomashyo turining bir birligi
10
bahosi (pul.birl.) – B = 30 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
50
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
26. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
5 1
A = 2 9 matritsa, mahsulot ishlab
4 8
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = (150 200 250 ) satr-matritsa, har bir xomashyo turining bir
80
ustun-matritsa koʻrinishida berilgan bo‘lsin.
75
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
27. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
1 2 5
foydalanadi. Xomashyo harajatlari – A = 8 6 3 matritsa, mahsulot ishlab
4 9 7
chiqarish rejasi – C = ( 90 115 140 ) satr-matritsa, har bir xomashyo turining bir
35
birligi bahosi (pul.birl.) – B = 50 ustun-matritsa koʻrinishida berilgan bo‘lsin.
65
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
28. Korxona 3 xil mahsulot ishlab chiqarish uchun 2 xil xomashyodan
2 5
A = 4 1 matritsa, mahsulot ishlab
6 9
foydalanadi. Xomashyo harajatlari –
chiqarish rejasi – C = ( 80 95 110 ) satr-matritsa, har bir xomashyo turining bir
22

23.

A.I.Sotvoldiyev, Sh.Sh.Omonov
50
ustun-matritsa koʻrinishida berilgan bo‘lsin.
80
birligi bahosi (pul.birl.) – B =
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
29. Korxona 2 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
4 2 3
foydalanadi. Xomashyo harajatlari – A =
matritsa, mahsulot ishlab
1
7
5
chiqarish rejasi – C = ( 40 90 ) satr-matritsa, har bir xomashyo turining bir birligi
50
bahosi (pul.birl.) – B = 60 ustun-matritsa koʻrinishida berilgan bo‘lsin. Rejani
70
bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning umumiy
bahosini aniqlang.
30. Korxona 3 xil mahsulot ishlab chiqarish uchun 3 xil xomashyodan
3 1 9
foydalanadi. Xomashyo harajatlari – A = 2 7 6 matritsa, mahsulot ishlab
5 4 3
chiqarish rejasi – C = ( 70 100 130 ) satr-matritsa, har bir xomashyo turining bir
40
birligi bahosi (pul.birl.) – B = 70 ustun-matritsa koʻrinishida berilgan bo‘lsin.
100
Rejani bajarish uchun sarflanadigan xomashyo miqdorini va xomashyoning
umumiy bahosini aniqlang.
23

24.

A.I.Sotvoldiyev, Sh.Sh.Omonov
DETERMINANTLAR NAZARIYASI
_________________________________________________________
Ushbu
a11 a12 ... a1n
a21 a22 ... a2 n
A=
... ... ...
an1 an 2 ... ann
n -tartibli kvadrat matritsa berilgan boʻlsin. U holda A matritsaning aniqlovchisi,
ya’ni n -tartibli determinanti deb,
a11 a12 ... a1n
a
a22 ... a2 n
det( A) = A = ∆ = 21
... ... ...
an1 an 2 ... ann
songa aytiladi.
Ikkinchi tartibli kvadrat matritsaning determinanti
a11 a12
= a11a22 − a21a12
a21 a22
kabi aniqlanadi.
Ikkinchi tartibli determinantni hisoblash quyidagicha sxematik koʻrinishda
amalga oshiriladi:
4 7
matritsaning determinantini hisoblang.
8
15
Misol. A =
Yechish:
A=
4 7
= 4 ⋅15 − 7 ⋅ 8 = 60 − 56 = 4.
8 15
_________________________________________________________
24

25.

A.I.Sotvoldiyev, Sh.Sh.Omonov
4-NAZORAT TOPSHIRIQLARI
Quyidagi 2-tartibli determinantlarni hisoblang.
1.
2 3
4 5
2.
2 8
9 7
3.
3 7
9 6
4.
7 3
2 1
5.
2 4
0 1
6.
3 5
2 1
7.
1 3
5 6
8.
4 7
1 3
9.
1 5
2 7
10.
1 4
2 5
11.
2 1
1 8
12.
2 4
1 3
13.
3 4
1 0
14.
3 5
4 1
15.
1 2
6 3
16.
1 2
2 3
17.
1 2
4 8
18.
1 2
−2 3
19.
−3 0
2 1
20.
4 7
−4 −8
21.
4 6
−3 1
22.
1 0
−6 2
23.
3 2
5 7
24.
3 8
4 5
25.
6 3
−2 5
26.
3 5
2 1
27.
−1 7
2 −15
28.
7 6
−4 −4
29.
5 −2
−6 3
30.
0 −1
5 −7
Uchinchi tartibli kvadrat matritsaning determinanti
a11 a12
a21 a22
a31 a32
a13
a23 = a11a22 a33 + a12 a23a31 + a13a21a32 − a13a22 a31 − a12 a21a33 − a11a23a32
a33
kabi aniqlanadi.
Uchinchi tartibli determinantda oʻz ishorasi va qarama-qarshi ishora bilan
olinadigan hadlarni eslab qolish uchun odatda ikki xil usuldan foydalaniladi. Bular
uchburchak va Sarrius usullari deb nomlanadi.
Uchburchak usuli. Uchinchi tartibli determinantni hisoblashning
uchburchak usuli quyidagicha sxematik koʻrinishda amalga oshiriladi:
Sarrius usuli. Uchinchi tartibli determinantni hisoblashning Sarrius usuli
quyidagicha amalga oshiriladi: determinant ustunlarining oʻng yoniga chapdagi
birinchi va ikkinchi ustunlar koʻchirib yoziladi. Hosil boʻlgan kengaytirilgan
25

26.

A.I.Sotvoldiyev, Sh.Sh.Omonov
jadvalda bosh diagonal yoʻnalishida joylashgan elementlar koʻpaytirilib musbat
ishora bilan, ikkilamchi diagonal yoʻnalishidagi elementlar koʻpaytirilib manfiy
ishora bilan olinib yigʻindi tuziladi. Buni sxema koʻrinishida quyidagicha
tasvirlash mumkin:
1 3 4
Misol. A= −2 5 7 matritsaning determinantini hisoblang.
0 2 1
Yechish: Determinantni uchburchak yoki Sarrius usulida hisoblasak,
quyidagi natijaga ega bo‘lamiz:
1 3 4
A =−2 5 7 =1 ⋅ 5 ⋅1 + 4 ⋅ (−2) ⋅1 + 3 ⋅ 7 ⋅ 0 − 4 ⋅ 5 ⋅ 0 − 1 ⋅ 7 ⋅ 2 − 3 ⋅ (−2) ⋅1 =−11.
0 2 1
_________________________________________________________
5-NAZORAT TOPSHIRIQLARI
Quyidagi 3-tartibli determinantlarni uchburchak usuli va Sarrius usuli
bo‘yicha hisoblang.
2 1 3
1. 0 4 7
6 5 1
2 3 4
2. 4 5 6
3 7 1
2 8 1
3. 9 7 5
3 2 1
3 7 1
4. 9 6 2
3 5 4
7 3 1
5. 2 1 4
8 3 2
2 4 5
6. 0 1 3
2 7 8
3 5 1
7. 2 1 2
3 1 7
1 3 5
8. 5 6 7
1 8 0
4 7 8
9. 1 3 5
2 4 6
1 4 7
10. 2 5 6
3 1 8
2 1 4
11. 1 8 3
2 7 4
2 4 7
12. 1 3 0
4 5 6
3 4 5
13. 1 0 1
2 3 1
3 5 1
14. 4 1 2
3 2 4
1 2 4
15. 6 3 1
3 1 8
26

27.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 2 4
16. 2 3 1
4 5 7
1 2 5
17. 4 8 9
3 2 0
1 2 3
18. 2 3 4
7 8 9
4 7 2
19. 3 8 3
0 1 2
3 2 4
20. 1 3 5
7 8 3
3 2 1
21. 5 7 3
4 5 7
1 2 5
22. 3 4 7
5 6 9
3 8 9
23. 4 5 1
1 1 0
3 8 1
24. 4 5 7
1 2 0
4 5 1
25. 3 8 4
1 3 4
2 1 3
26. 5 3 2
1 4 3
3 2 4
27. 4 1 2
5 2 3
2 4 1
28. 3 4 2
4 1 3
2 5 7
29. 2 8 5
8 7 3
1 4 6
30. 2 0 7
3 5 2
Determinantlar quyidagi xossalarga ega:
1) Agar determinantni biror satri (yoki ustuni)ning barcha elementlari nolga
teng boʻlsa, u holda uning qiymati nolga teng boʻladi. Masalan,
0 5 4
0 2 −3 = 0 ⋅ 2 ⋅ 6 + 5 ⋅ (−3) ⋅ 0 + 4 ⋅ 0 ⋅1 − 4 ⋅ 2 ⋅ 0 − 5 ⋅ 0 ⋅ 6 − 0 ⋅ (−3) ⋅1 = 0.
0 1 6
2) Diagonal matritsaning
koʻpaytmasiga teng, ya’ni
determinanti
det( A) = a11 ⋅ a22 ⋅ ... ⋅ ann =
diagonal
elementlarining
n
∏ aii .
i =1
Masalan,
2 0 0
0 5 0 =2 ⋅ 5 ⋅ (−1) =−10.
0 0 −1
3) Yuqori (yoki quyi) uchburchakli matritsalarning determinantlari uning
bosh diagonal elementlari koʻpaytmasiga teng, ya’ni
det( A) = a11 ⋅ a22 ⋅ ... ⋅ ann =
Masalan,
27
n
∏ aii .
i =1

28.

A.I.Sotvoldiyev, Sh.Sh.Omonov
2 7 −10
0 5 6 = 2 ⋅ 5 ⋅1 = 10.
0 0 1
4) Determinantning biror satri (yoki ustuni) elementlarini k
( k ≠ 0 ) songa
koʻpaytirish, determinantni shu songa koʻpaytirishga teng kuchlidir. Shuningdek,
biror satr (yoki ustun) elementlarining umumiy koʻpaytuvchisini determinant
belgisidan tashqariga chiqarish mumkin, ya’ni
a11 a12
k ⋅ a21 a22
a31 a32
a13 ka11 ka12
a23= a21 a22
a33
a31 a32
ka13 a11 a12
a23= a21 a22
a33
a31 a32
ka13
ka23 .
ka33
Masalan,
1 0 3
2 ⋅ 5 −4 1 = 2 ⋅ (−8 + 15 + 0 + 24 − 1 − 0) = 60;
2 1 2
2 ⋅1 2 ⋅ 0 2 ⋅ 3 2 0 6
5
−4
1 =5 −4 1 =−16 + 30 + 0 + 48 − 2 − 0 =60;
2
1
2
2 1 2
2 ⋅1 0 3
2 0 3
2 ⋅ 5 −4 1 =10 −4 1 =−16 + 30 + 0 + 48 − 2 − 0 =60.
2⋅2 1 2
4 1 2
5) n -tartibli determinant uchun quyidagi tenglik oʻrinli:
det(kA=
) k n ⋅ det( A) .
6) Determinantda ikkita satr (yoki ustun) oʻrinlari almashtirilsa, u holda
uning ishorasi oʻzgaradi. Masalan,
2 −3 1
−1 5 0 =10 + 2 + 0 − 20 − 0 − 3 =−11.
4 −2 1
Endi bu determinantda birinchi va uchinchi ustunlarining oʻrinlarini
almashtirib hisoblaymiz:
1 −3 2
0 5 −1 = 20 + 0 + 3 − 10 − 2 − 0 = 11.
1 −2 4
Bundan koʻrinib turibdiki, determinantlar faqat ishorasi bilan farq qiladi.
7) Agar determinant ikkita bir xil satr (yoki ustun)ga ega boʻlsa, u holda
uning qiymati nolga teng boʻladi. Masalan,
28

29.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 3 −2
1 3 −2 = 0 + 8 − 18 + 18 − 8 − 0 = 0.
3 −4 0
8) Agar determinantni biror satri (yoki ustuni) elementlariga boshqa satri
(yoki ustuni)ning mos elementlarini biror songa koʻpaytirib qoʻshilsa, u holda
uning qiymati oʻzgarmaydi, ya’ni
a11
a12
⋅⋅⋅
a1n
a11
a12
⋅⋅⋅
a1n
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
ai1
ai 2
⋅⋅⋅
ain
ai1 + ka j1
ai 2 + ka j 2
⋅⋅⋅
ain + ka jn
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅ =
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
a j1
a j2
⋅⋅⋅
a jn
a j1
a j2
⋅⋅⋅
a jn
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
an1
an 2
⋅⋅⋅
ann
an1
an 2
⋅⋅⋅
ann
.
Masalan,
1 2 3
1
2
3
2 4 5 = 2 + 1⋅ 2 4 + 2 ⋅ 2 5 + 3 ⋅ 2 .
3 5 1
3
5
1
Haqiqatan ham, tenglikning chap tarafi
1 2 3
2 4 5 =+
4 30 + 30 − 36 − 4 − 25 =
−1,
3 5 1
oʻng tarafi esa
1
2
3
2 + 1⋅ 2 4 + 2 ⋅ 2 5 + 3 ⋅ 2 =
8 + 66 + 60 − 72 − 55 − 8 =
−1.
3
5
1
Demak, tenglik oʻrinli.
9) Agar determinantni ikki satri (yoki ustuni)ning mos elementlari
proporsional boʻlsa, u holda uning qiymati nolga teng boʻladi, ya’ni
a11 a12 a13
a11 a12 ka11
ka=
ka13 a=
ka21 0.
11 ka12
21 a22
a31 a32 a33
a31 a32 ka31
Masalan,
6 8 4 2⋅3 2⋅4 2⋅2
12 6 8 = 12
6
8 =72 + 192 + 192 − 72 − 192 − 192 =0.
3 4 2
3
4
2
29

30.

A.I.Sotvoldiyev, Sh.Sh.Omonov
10) Transponirlash natijasida determinantning qiymati oʻzgarmaydi.
Masalan,
−1 3 2 −1 0 5
0 6 2 = 3 6 4 =−6 + 0 + 30 − 60 + 8 − 0 =−28.
5 4 1
2 2 1
11) Agar determinantni biror satri (yoki ustuni)ning har bir elementi ikki
qoʻshiluvchi yigʻindisidan iborat boʻlsa, u holda determinant ikki determinant
yigʻindisiga teng boʻlib, ulardan birining tegishli satri (yoki ustuni) birinchi
qoʻshiluvchilaridan, ikkinchisining tegishli satri (yoki ustuni) ikkinchi
qoʻshiluvchilaridan iborat boʻladi, ya’ni
a11
⋅⋅⋅
ai1 + bi1
⋅⋅⋅
an1
a12
⋅⋅⋅
a1n
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
ai 2 + bi 2 =
ain + bin
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
an 2
ann
⋅⋅⋅
a11
⋅⋅⋅
ai1
⋅⋅⋅
an1
a12
⋅⋅⋅
ai 2
⋅⋅⋅
an 2
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
a1n
a11
⋅⋅⋅
⋅⋅⋅
ain + bi1
⋅⋅⋅
⋅⋅⋅
ann
an1
a12
⋅⋅⋅
bi 2
⋅⋅⋅
an 2
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
a1n
⋅⋅⋅
bin .
⋅⋅⋅
ann
12) Agar determinantni satr (yoki ustun)laridan biri qolgan satr (yoki
ustun)larining chiziqli kombinatsiyasidan iborat boʻlsa, u holda uning qiymati
nolga teng boʻladi. Masalan,
2 3 16
2 3 2⋅2 + 4⋅3
−2 1 0 = −2 1 −2 ⋅ 2 + 4 ⋅1 =0.
3 −2 −2
3 −2 3 ⋅ 2 − 4 ⋅ 2
13) Toq tartibli har qanday qiya simmetrik matritsaning determinanti nolga
teng bo‘ladi. Masalan,
0 −3 4
3 0 −5 = 0 + 60 − 60 + 0 + 0 + 0 = 0.
−4 5 0
14) Bir xil tartibli ikkita matritsalar koʻpaytmasining determinanti, bu
matritsalar determinantlarining koʻpaytmasiga teng, ya’ni
det( A ⋅ B=
) det( A) ⋅ det( B ).
Bizga n -tartibli kvadrat matritsa berilgan boʻlsin.
Ta’rif. n -tartibli A kvadrat matritsaning 1 ≤ k ≤ n − 1 shartni qanoatlantiruvchi
ixtiyoriy k ta satrlari va k ta ustunlari kesishgan joyda turgan elementlardan
tashkil topgan k -tartibli matritsaning determinanti n -tartibli determinantning k tartibli minori deb ataladi.
30

31.

A.I.Sotvoldiyev, Sh.Sh.Omonov
k -tartibli minor sifatida A kvadrat matritsaning n − k ta satr va n − k ta
ustunini oʻchirishdan hosil boʻlgan determinant deb ham qarash mumkin.
Ta’rif. n -tartibli A kvadrat matritsada k -tartibli M minor turgan satrlar va
ustunlar oʻchirib tashlangandan soʻng, qolgan (n − k ) -tartibli M ′ minorga M
minorning toʻldiruvchisi deyiladi va aksincha.
Shunday qilib, determinantning oʻzaro toʻldiruvchi minorlar jufti haqida
gapirish mumkin. Xususiy holda, aij element va determinantning i -satri va j ustunini oʻchirishdan hosil boʻlgan (n − 1) -tartibli minor oʻzaro toʻldiruvchi
minorlar juftini hosil qiladi.
Ta’rif. aij minorning (elementning) algebraik toʻldiruvchisi deb, Aij = (−1)i + j M ij
songa aytiladi.
Laplas teoremasi. n -tartibli determinantning qiymati uning ixtiyoriy satr (yoki
ustun) elementlari bilan, shu elementlarga mos algebraik toʻldiruvchilar
koʻpaytmalarining yigʻindisiga teng, ya’ni
a11 a12
... ...
=
∆ ai1 ai 2
... ...
an1 an 2
... a1n
... ...
... ain= ai1 Ai1 + ai 2 Ai 2 + ... + ain A=
in
... ...
... ann
n
∑ (−1)i + j aij M ij .
j =1
Bu formulaga ∆ -determinantni i -satr elementlari boʻyicha yoyish formulasi
deyiladi.
2 1 3
Misol. ∆ = 5 3 2 determinantni Laplas formulasi bilan hisoblang.
1 4 3
Yechish: Berilgan determinantni birinchi satr elementlari boʻyicha yoysak,
∆=
2
5
1
1
3
4
3
2 = 2 A11 + A12 + 3 A13= 2(−1)1+1 ⋅ M11 + (−1)1+ 2 ⋅ M12 + 3(−1)1+3 ⋅ M13=
3
3 2 5 2
5 3
=
2⋅
−
+ 3⋅
=−
2(9 8) − (15 − 2) + 3(20 − 3) =
2 − 13 + 51 =
40.
4 3 1 3
1 4
31

32.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 0
2 −1
Misol. ∆ =
3 2
1 0
3
4
1
6
2
1
determinantni Laplas formulasi bilan hisoblang.
5
2
Yechish: Berilgan determinantni ikkinchi ustun elementlari boʻyicha yoyib
chiqamiz. Bu ustunda 2 ta noldan farqli element boʻlgani uchun natijada 2 ta 3tartibli determinant hosil boʻladi.
∆=
1
0
3 2
2
−1
4 1
3
1
2
0
1 5
6 2
=−1 ⋅ (−1)
2+ 2
1 3 2
1 3 2
3+ 2
3 1 5 + 2 ⋅ (−1) 2 4 1 =−21.
1 6 2
1 6 2
Yoki avval a32 = 2 elementni nolga keltirishimiz mumkin. Buning uchun 2-satrni 2
ga koʻpaytirib 3-satrga qoʻshamiz va hosil boʻlgan determinantni 2-ustun
elementlariga nisbatan yoyamiz va hisoblaymiz:
1 0
2 −1
∆=
3 2
1 0
3
4
1
6
2 1
1 2
=
5 7
2 1
0
−1
0
0
3 2
1 3 2
4 1
2+ 2
= −1 ⋅ (−1) ⋅ 7 9 7 = −21.
9 7
1 6 2
6 2
Koʻrinib turibdiki, Laplas teoremasidan yuqorida keltirilgan xossalar bilan
birgalikda foydalanish determinantni hisoblashni ancha osonlashtiradi. Buning
uchun biror satr yoki ustunni tanlab olib, shu ustun yoki satrdagi elementlarni
determinantning xossalaridan foydalanib, iloji boricha nollarga keltirishimiz kerak
boʻladi. Soʻngra, Laplas teoremasi yordamida determinantning tartibini bittaga
kamaytirishimiz mumkin.
_________________________________________________________
32

33.

A.I.Sotvoldiyev, Sh.Sh.Omonov
6-NAZORAT TOPSHIRIQLARI
1. Quyidagi 4-tartibli determinantlarni berilgan satr va ustun
elementlari bo‘yicha yoyib hisoblang.
5 0
1 −1
1. 4 1
1 1
4
2
2
1
2
1
0
1
3 1
4 −1
2. 1 −1
4 −1
2
2
1
2
3
4
1
5
=
i 3;=
j 2
=
i 2;=
j 3
1 8 2 −3
3 −2 0 4
4. 5 −3 7 −1
3 2 0 2
2 −5 1
−3 7 −1
5. 5 −9 2
4 −6 1
=
i 1;=
j 2
=
i 2;=
j 1
3 −3 −5 8
−3 2 4 −6
7. 2 −5 −7 5
4 3 2 −6
2 −5 4
3 −4 7
8. 4 −9 8
−3 2 −5
1
2
3. 3
4
2
2
7
2
3
5
5
3
3 −5 −2 2
−4 7 4 4
10. 4 −9 −3 7
2 −9 −3 2
3 −5 2 −4
−3 4 −5 3
11. −5 7 −7 5
8 −8 5 −6
=
i 1;=
j 1
=
i 2;=
j 3
3
7
3
5
7
2
5
4
=
i 2;=
j 3
8
−8
16. 4
0
7 2 10
2 7 10
4 4 5
4 −3 2
=
i 1;=
j 2
6 −5 8 4
9 7 5 2
14. 7 5 3 7
−4 8 −8 −3
=
i 3;=
j 1
2 −1
0 1
17. 3 −1
3 1
1 0
2 −1
2 3
6 1
=
i 1;=
j 2
33
4
3
2
1
−3 9 3 6
−5 8 2 7
6. 4 −5 −3 −2
7 8 −4 −5
=
i 2;=
j 4
=
i 3;=
j 3
6
5
4
6
3
2
1
2
=
i 4;=
j 3
i 2;=
j 3
=
7
3
13. 5
5
2
1
2
3
3 −3 −2 −5
2 5 4 6
9. 5 5 8 7
4 4 5 6
=
i 4;=
j 1
3 2
9 −8
12. 5 −8
6 −5
2 2
5 10
5 8
4 7
=
i 3;=
j 2
7 3
8 −9
15. 7 −2
5 −3
2
4
7
3
6
9
3
4
=
i 4;=
j 3
2
2
18. 6
2
3 −3 4
1 −1 2
2 1 0
3 0 −5
=
i 4;=
j 4

34.

A.I.Sotvoldiyev, Sh.Sh.Omonov
3 −1
5 2
19. 0 2
6 −2
4 2
0 1
1 −3
9 8
=
i 2;=
j 2
3 5
1 2
22. −2 −3
1 3
7
3
3
5
1 2
1 −1
20. 2 1
1 1
3
1
0
2
1
4
1
4
2 0
1 1
21. 0 1
−1 −1
=
i 3;=
j 4
2
4
2
4
=
i 4;=
j 3
1 −2 3 4
2 1 −4 3
25. 3 −4 −1 −2
4 3 2 −1
=
i 3;=
j 1
−1 −2 1 1
2 3 0 6
28. 2 −2 1 0
3 1 −2 −1
=
i 4;=
j 3
1
0
23. 3
2
2
1
0
3
3
2
1
0
0
3
2
1
1 1 1
2 4 8
3 9 27
4 16 64
1
0
24. 3
2
2 0
1 2
3 −2
3 −2
14
20
14
12
3
2
1
0
0
3
.
2
1
=
i 2;=
j 3
−1
1
27. −2
2
1 −2
2 2
3 1
3 −2
3
3
0
0
=
i 3;=
j 2
=
i 2;=
j 3
2 −1
3 4
29. 2 −1
1 2
1
2
2
1
=
i 1;=
j 3
=
i 1;=
j 1
1
1
26. 1
1
2
0
1
0
4
−2
30. 0
5
=
i 2;=
j 3
3 −2 −1
1 −4 3
4 1 −1
0 1 −1
i 3;=
j 4
=
2. Quyidagi yuqori tartibli determinantlarni nol yig‘ish usuli yordamida
(determinantning xossalaridan foydalanib) hisoblang.
−3 9 3 6
−5 8 2 7
2.
4 −5 −3 −2
7 −8 −4 −5
2 −5 4
3 −4 7
3.
4 −9 8
−3 2 −5
3
5
5
3
3 −5 2 4
−3 4 −5 3
4.
−5 7 −7 5
8 −8 5 −6
6 −5 8 4
9 7 5 2
5.
7 5 3 7
−4 8 −8 −3
2 −5 1
−3 7 −1
6.
5 −9 2
4 −6 1
2
4
7
2
3 −3 5 8
−3 2 4 6
7.
2 −5 −7 5
−4 3 5 −6
3 −5 −2 2
−4 7
4 4
8.
4 −9 −3 7
2 −6 −3 2
7
3
9.
5
5
7 3
8 −9
1.
7 −2
5 −3
2
4
7
3
6
9
3
4
34
6
5
4
6
3
7
3
5
7
2
5
4

35.

A.I.Sotvoldiyev, Sh.Sh.Omonov
1 −2 3 4
2 4 −4 3
10.
3 −4 −1 −2
4 3 2 −1
1
3
11.
5
7
−3
−5
−7
−1
5 7
7 −1
1 −3
3 −5
5
3
12.
3
4
7
2
7
3
1 −3 4
0 −2 3
2 0 −5
3 −5 0
2
2
14.
6
2
3 −3 4
1 −1 2
2 1 0
3 0 −5
6
5
15.
4
7
5 9 3
8 8 −2
5 5 2
8 10 2
0
1
13.
3
4
8 7
9 −3
4 2
9 6
7 4 −5 −3
−8 −5 8 9
16.
−4 −3 2 3
−5 −2 7 6
2 4 −4 3
−6 −9 7 −5
17.
−3 −3 4 −2
2 7 4 2
3
5
18.
4
7
−9
−8
−5
−8
4
3
19.
1
2
2 3 −4 5
3 −5 2 4
20.
5 4 3 −2
−4 2 5 3
2
4
21.
3
1
3
5
7
2
4
6
1
3
1
0
2
7
2 −5 1
−3 7 −1
23.
5 −9 2
4 −6 1
2
3
24.
−1
−1
1
2
0
2
0
1
1
1
2
0
3
3
5
8
3
4
1
4
4
8
1
2
1
3
2 −5 4
3 4 7
22.
4 −9 8
−3 2 −5
3
5
5
3
2
4
7
2
−3
−2
−3
−4
−6
−7
−2
−3
−3 9 3 6
−5 8 2 7
25.
4 −5 −3 −2
7 −8 −4 −5
3 −3 −5 −8
−3 2 4 −6
26.
2 −5 −7 5
−4 3 5 −6
3 −5 −2 2
−4 7 4 4
27.
4 −9 −3 7
2 −6 −3 2
1
2
28.
3
1
3 −3 −2 −5
2 5 4 6
29.
5 5 8 7
4 4 5 6
3 2
9 −8
30.
5 −8
6 −5
4
5
1
2
7
6
8
3
2
3
4
0
35
2 2
5 10
5 8
4 7

36.

A.I.Sotvoldiyev, Sh.Sh.Omonov
MATRITSA RANGI. TESKARI MATRITSA
_________________________________________________________
Ushbu
a11 a12 ... a1n
a21 a22 ... a2 n
A=
...
... ...
am1 am 2 ... amn
m × n o‘lchovli matritsa berilgan bo‘lsin.
Ta’rif. Ixtiyoriy oʻlchovli matritsaning bir necha satr yoki ustunlarini oʻchirishdan
hosil bo‘lgan kvadrat matritsa determinantiga matritsa osti minori deyiladi. Bu
kvadrat matritsaning tartibi matritsa osti minorning tartibi deb ataladi.
Izoh. Agar berilgan matritsa kvadrat shaklda boʻlsa, uning eng katta tartibli
minori oʻziga teng.
Masalan,
4 5 7
A = 2 1 4
3 7 6
matritsada
4 5 7
o‘zi orqali M 3 = 2 1 4 – 3-tartibli;
3 7 6
1-satr va 1-ustunni oʻchirish orqali M 2 =
1 4
– 2-tartibli;
7 6
1 va 2-satrlar hamda 1 va 2-ustunlarni oʻchirish orqali M1 = 6 – 1-tartibli
va hokazo matritsa osti minorlari mavjud.
Ta’rif. A matritsaning rangi deb, noldan farqli matritsa osti minorlarining eng
katta tartibiga aytiladi va rang ( A) = r ( A) koʻrinishida ifodalanadi.
Matritsa rangining xossalari:
1) agar A matritsa m × n oʻlchovli boʻlsa, u holda rang ( A) ≤ min(m; n);
2) agar A matritsaning barcha elementlari nolga teng boʻlsa, u holda
rang ( A) = 0;
36

37.

A.I.Sotvoldiyev, Sh.Sh.Omonov
3) agar A matritsa n -tartibli kvadrat matritsa va A ≠ 0 boʻlsa, u holda
rang ( A) = n.
1 −2 3
matritsaning rangini aniqlang.
−2 4 −7
Yechish: Berilgan matritsa 2 × 3 oʻlchovli boʻlgani uchun satrlar va ustunlar
Misol. A =
sonini taqqoslaymiz va kichigini, ya’ni 2 ni tanlaymiz. Matritsadan ikkinchi tartibli
minorlar ajratamiz va ularning qiymatini hisoblaymiz. Bu jarayonni noldan farqli
ikkinchi tartibli minor topilguncha davom ettiramiz:
1 −2
M2 =
=0,
−2 4
1
3
M2 =
=−1 ≠ 0.
−2 −7
Berilgan matritsadan noldan farqli eng yuqori ikkinchi tartibli minor ajraldi.
Demak, ta’rifga binoan, A matritsaning rangi 2 ga teng, ya’ni rang ( A) = 2 .
Matritsa rangi uning ustida quyidagi almashtirishlar bajarganda
oʻzgarmaydi:
1) biror satri (ustuni)ning har bir elementini noldan farqli songa
koʻpaytirganda;
2) satr (ustun)larini oʻrinlari almashtirilganda;
3) biror satri (ustuni)ning elementlariga uning boshqa parallel satri (ustuni)
mos elementlarini noldan farqli songa koʻpaytirib, soʻngra qoʻshganda;
4) barcha elementlari noldan iborat satri (ustuni) tashlab yuborilganda;
5) transponirlanganda.
Teorema. Elementar almashtirishlar matritsa rangini oʻzgartirmaydi.
Masalan,
3 1 −2 −1
A = 2 −1 1 −2
−5 −2 3 1
matritsada birinchi satrni 2 ga va ikkinchi satrni –3 ga koʻpaytirib, birinchini
ikkinchiga qoʻshsak, soʻngra yana birinchi satrni 5 ga, uchunchi satrni 3 ga
koʻpaytirib, natijalarni qoʻshsak,
3 1 −2 −1
−
0
5
7
4
0 −1 −1 −2
matritsa hosil boʻladi.
Bu matritsada ikkinchi satrni 1 ga, uchunchi satrni 5 ga koʻpaytirib, ikkinchi
satrni uchunchi satrga qoʻshsak,
37

38.

A.I.Sotvoldiyev, Sh.Sh.Omonov
3 1 −2 −1
0 5 −7 4
0 0 −12 −6
matritsa hosil boʻladi.
2 −3 3 0
−4 2 −4 5
B=
−2 −1 −1 5
matritsani olib, yuqoridagi singari almashtirishlarni bajarsak,
2 −3 3 0 2 −3 3 0 2 −3 3 0
B=
−4 2 −4 5 ~ 0 −4 2 5 ~ 0 −4 2 5
−2 −1 −1 5 0 −4 2 5 0 0 0 0
hosil boʻladi.
Teorema. Pog‘onasimon matritsaning rangi, uning noldan farqli satrlari soniga
teng.
Ixtiyoriy matritsaning rangini aniqlash uchun yuqorida kо‘rsatilgan qoida
bо‘yicha elementar almashtirishlar yordamida matritsa pog‘onasimon matritsaga
keltiriladi:
a11 a12
0 a22
A=
... ...
0
0
... a1r
... a2 r
... ...
... arr
... a1k
... a2 k
,
... ...
... ark
bu yerda aii ≠ 0,=
i 1,..., r , r ≤ k .
Izoh. Pog‘onasimon matritsaning rangi r ga teng.
1 −2 1 3
Misol. A = 3 1 0 7 matritsaning rangini aniqlang.
2 3 −1 4
Yechish: A matritsaning rangi rang ( A) ≤ min(3; 4) =
3. Berilgan matritsa
ustida quyidagicha elementar almashtirishlar bajaramiz:
3 1 −2 1
3
1 −2 1 3 1 −2 1
A 3 1 0 7 ~ 0 7 −3 −2 ~ 0 7 −3 −2 .
=
2 3 −1 4 0 7 −3 −2 0 0 0
0
Demak, A matritsa pog‘onasimon matritsa ko‘rinishiga keltirildi. Uning uchinchi
satrini barcha elementlari nollardan iborat boʻlganligi sababli, berilgan matritsa
rangi rang ( A) = 2 ga teng.
38

39.

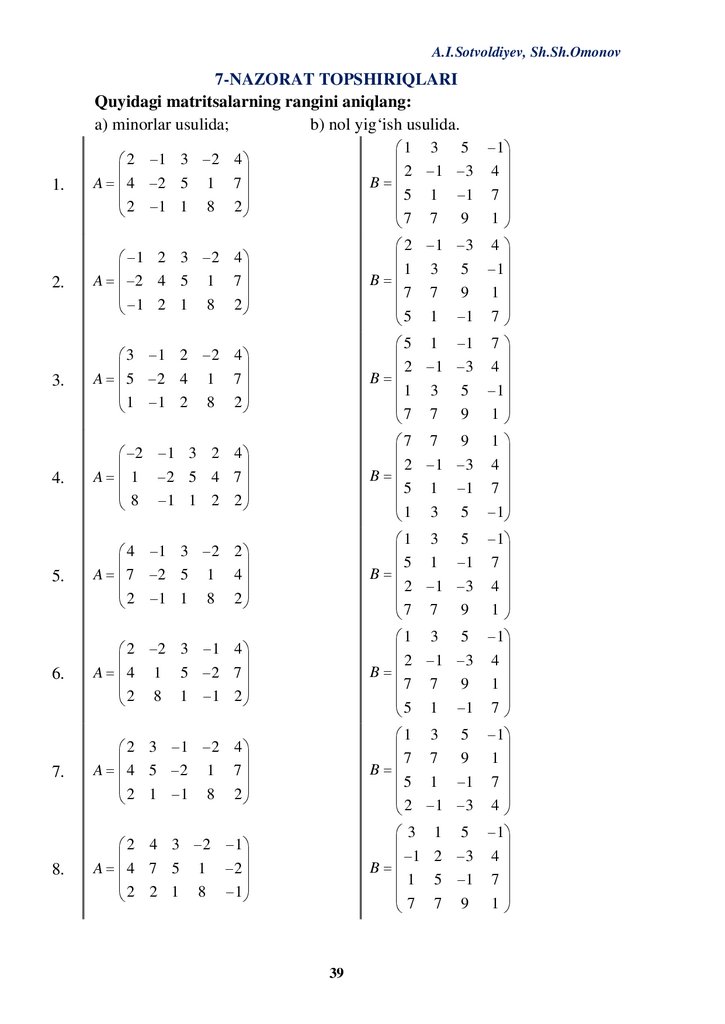
A.I.Sotvoldiyev, Sh.Sh.Omonov
7-NAZORAT TOPSHIRIQLARI
Quyidagi matritsalarning rangini aniqlang:
a) minorlar usulida;
b) nol yig‘ish usulida.
1.
2 −1 3 −2 4
=
A 4 −2 5 1 7
2 −1 1 8 2
2.
−1 2 3 −2 4
A= −2 4 5 1 7
−1 2 1 8 2
3.
3 −1 2 −2 4
=
A 5 −2 4 1 7
1 −1 2 8 2
1 3 5 −1
2 −1 −3 4
B=
5 1 −1 7
7 7 9 1
2 −1 −3 4
1 3 5 −1
B=
7 7 9 1
5 1 −1 7
5 1 −1 7
2 −1 −3 4
B=
1 3 5 −1
7 7 9 1
7 7 9 1
2 −1 −3 4
B=
5 1 −1 7
1 3 5 −1
1 3 5 −1
−
5
1
1
7
B=
2 −1 −3 4
7 7 9 1
1 3 5 −1
2 −1 −3 4
B=
7 7 9 1
5 1 −1 7
1 3 5 −1
7 7 9 1
B=
5 1 −1 7
2 −1 −3 4
3 1 5 −1
−
1 2 −3 4
B=
1 5 −1 7
7 7 9 1
−2 −1 3 2 4
A 1 −2 5 4 7
4. =
8 −1 1 2 2
5.
4 −1 3 −2 2
A 7 −2 5 1 4
=
2 −1 1 8 2
2 −2 3 −1 4
A 4 1 5 −2 7
=
6.
2 8 1 −1 2
2 3 −1 −2 4
A 4 5 −2 1 7
7.=
2 1 −1 8 2
2 4 3 −2 −1
=
A 4 7 5 1 −2
8.
2 2 1 8 −1
39

40.

A.I.Sotvoldiyev, Sh.Sh.Omonov
9.
1 −1
2 4
5 7
7 1
5 3 1 −1
9 7 7 1
B=
−1 1 5 7
−3 −1 2 4
5 3 1 −4
− −
3 1 2 4
B=
9 7 7 1
−1 1 5 7
−1 3 5 −1
−
−
4
1
1
2
B=
7 1 9 5
1 7 −3 7
2 3 5 −1
4 −1 −3 4
B=
10 1 −1 7
14 7 9 1
1 3 5 −1
4 −2 −6 8
B=
10 2 −2 7
7 7 9 1
1 3 5 −1
−
2 1 3 −4
B=
5 1 −1 7
14 14 16 2
2 6 10 −2
2 −1 −3 4
B=
5 1 −1 7
7 7 9 1
2 3 5 −1
4 −1 −3 4
B=
10 1 −1 7
14 7 9 1
5 3
− −
3 1
B=
−1 1
9 7
2 −1 4 −2 3
=
A 4 −2 7 1 5
2 −1 2 8 1
2 −1 3 4 −2
A 4 −2 5 7 1
10. =
2 −1 1 2 8
11.
4 −2 5 1 7
A = 2 −1 3 −2 4
2 −1 1 8 2
2 −1 3 −2 4
A 4 −2 5 1 7
12. =
2 −1 1 8 2
4 −2 6 −4 8
A 4 −4 10 2 14
13. =
4 −2 2 16 4
2 −1 6 −2 4
A 4 −2 10 1 7
14. =
2 −1 2 8 2
15.
6 1 3 −2 4
A = 12 2 5 1 7
6 1 1 8 2
16.
2 4 2 1 3
A = −1 −2 −1 0 3
3 5 1 −2 4
1 −1 3 −2 4
A 2 −2 5 1 7
17. =
1 −1 1 8 2
40

41.

A.I.Sotvoldiyev, Sh.Sh.Omonov
18.
2 6 10 −2
4 −2 −6 8
B=
5 1 −1 7
7 7 9 1
1 1 3 5
−
4 2 −1 −3
B=
−7 5 1 −1
−1 7 7 9
7 7 9 1
−
2 1 3 4
B=
2 6 10 −2
5 1 −1 7
4 −2 6 8
7
7
9
1
B=
1 3 5 1
5 1 −1 7
2 6 5 −1
4 −2 −5 4
B=
10 2 −1 7
14 14 9 1
1 3 5 1
4 −2 −6 8
B=
5 1 −1 7
7 7 9 1
10 2 −2 14
7 7 9 1
B=
1 −3 5 −1
2 −1 −3 4
−2 3 1 5
8 −1 2 −3
B=
14 1 5 −1
2 7 7 9
2 −1 −3 4
1 3 5 −1
B=
7 7 9 1
10 2 −2 14
1 3 3 2 4
A = 2 6 5 1 7
1 3 1 8 2
6 1 3 2 4
=
19. A 12 2 5 −1 7
6 1 1 −8 2
20.
4 1 −1 3 4
A = 7 2 −2 5 −2
2 1 −1 1 −16
8 3 1 −2 −2
=
21. A 14 5 2 −4 1
4 1 1 −2 8
3 1 −3 −2 4
=
A 5 2 −6 1 7
22.
1 1 −3 8 2
6 −1 1 −2 4
A 10 −2 2 1 7
23. =
2 −1 1 8 2
24.
4 −2 2 16 4
A = 2 −1 3 −2 4
4 −2 5 1 7
25.
8 −4 10 2 14
2 −1 3 −2 4
A=
2 −1 1 8 2
4 −2 6 −4 8
A 8 −4 10 2 14
26. =
4 −2 2 16 4
41

42.

A.I.Sotvoldiyev, Sh.Sh.Omonov
27.
1 −3 5
5 −1 −1
B=
2 1 −3
7 −7 9
6 1 3 −2 4
A = 12 2 5 1 7
6 1 1 8 2
1 3 5 −1
2 −1 −3 4
B=
7 7 9 1
5 1 −1 7
−1 3 −5 1
4 −1 1 2
B=
7 1 −9 5
1 7 3 7
2 −3 5 −1
−
4
1
3
4
B=
10 −1 −1 7
14 −7 9 1
1 −1 3 −2 4
A 2 −2 5 1 7
28. =
1 −1 1 8 2
29.
1
7
4
1
4 −2 5 1 7
A = 2 −1 3 −2 4
2 −1 1 8 2
2 −1 3 4 −2
A 4 −2 5 7 1
30. =
2 −1 1 2 8
Ta’rif. A kvadrat matritsaning determinanti noldan farqli boʻlsa, u holda bunday
matritsa xosmas matritsa, aks holda A matritsa xos matritsa deyiladi.
Misol.
1 −2 3
1 −2
=
A 0 4 −1 va B =
−5 10
5 0 0
matritsalarni xos yoki xosmas ekanligini aniqlang.
Yechish: Berilgan matritsalarning determinantlarini hisoblaymiz:
1 −2 3
A =0 4 −1 =10 − 60 =−50 ≠ 0,
5 0 0
B =
1 −2
= 10 − 10 = 0
−5 10
Demak, A – xosmas matritsa, B esa xos matritsa.
Ta’rif. A kvadrat matritsaning har bir aij elementini unga mos algebraik
toʻldiruvchisi bilan almashtirish natijasida hosil qilingan matritsa ustida
transponirlash amalini bajarishdan hosil boʻlgan A matritsa berilgan matritsaga
qo‘shma matritsa deyiladi.
42

43.

A.I.Sotvoldiyev, Sh.Sh.Omonov
a11 a12
a21 a22
... ...
A=
ai1 ai 2
... ...
a
n1 an 2
... a1 j
... a2 j
...
...
...
aij
... ...
... anj
... a1n
... a2 n
... ...
... ain
... ...
... ann
⇒
A11
A12
...
A=
A1 j
...
A
1n
A21
A22
...
A2 j
... Ai1
... Ai 2
... ...
... Aij
... ... ...
A2 n ... Ain
... An1
... An 2
... ...
... Anj
... ...
... Ann
1 −2 3
Misol.
A 0 4 −1 matritsa uchun qoʻshma matritsa toping.
=
5 0 0
Yechish: Matritsaning barcha elementlariga mos algebraik toʻldiruvchilarni
hisoblaymiz:
A11 =
(−1)1+1 ⋅
4 −1
0 −1
0 4
=
−5; A13 =
(−1)1+ 2 ⋅
(−1)1+3 ⋅
=
=
−20;
0; A12 =
5 0
5 0
0 0
A21 =
(−1) 2+1 ⋅
−2 3
1 3
=
−15;
=
0; A22 =
(−1) 2+ 2 ⋅
0 0
5 0
A31 =
(−1)3+1 ⋅
−2 3
=
−10;
4 −1
A32 =
(−1)3+ 2 ⋅
A23 =
(−1) 2+3 ⋅
1 −2
=
−10;
5 0
1 3
1 −2
=
1; A33 =
=
(−1)3+3 ⋅
4.
0 −1
0 4
Shunday qilib, berilgan A matritsaga qoʻshma matritsa
T
−5 −20
0 −10
0
0
A = 0 −15 −10 = −5 −15 1
−10 1
−20 −10 4
4
koʻrinishda aniqlanadi.
−1
−1
Ta’rif. A kvadrat matritsa uchun AA
=
A=
A E tenglik bajarilsa, A−1 matritsa
A matritsaga teskari matritsa deyiladi.
Ta’rifga asosan,
−1
det( AA
=
) det(
=
E) 1
boʻlganligi uchun teskari matritsa mavjud boʻlsa, det( A) ≠ 0 ekanligini hosil
qilamiz. Agar det( A) = 0 boʻlsa, teskari matritsa mavjud emas.
Odatda matritsaga teskari matritsa topishning 2 xil usulidan
foydalanamiz:
1. Agar A matritsa xosmas boʻlsa, u holda uning uchun yagona A−1 matritsa
mavjud boʻladi va u quyidagi tenglik bilan aniqlanadi:
43

44.

A.I.Sotvoldiyev, Sh.Sh.Omonov
A−1 =
1
A,
det( A)
bunda A matritsa A matritsaga qoʻshma matritsa.
1 2 3
Misol. A = 4 5 6 matritsaga teskari matritsani toping.
7 8 0
Yechish:
1) A matritsaning determinantini topamiz:
det( A) = 1 ⋅
5 6
4 6
4 5
− 2⋅
+ 3⋅
=
8 0
7 0
7 8
=
−48 − 2 ⋅ (−42) + 3 ⋅ (32 − 35) =
−48 + 84 − 9 =
27 ≠ 0
demak, A−1 mavjud.
2) A matritsa barcha elementlarining algebraik to‘ldiruvchilarini topamiz:
A11 =−
( 1)1+1 ⋅
5 6
=5 ⋅ 0 − 6 ⋅ 8 =−48;
8 0
2 3
2 3
= −3;
A21 =
−
=
24; A31 =
5 6
8 0
A12 =−
( 1)1+ 2 ⋅
4 6
=−(4 ⋅ 0 − 6 ⋅ 7) =42;
7 0
A22 =
A13 =−
( 1)1+3 ⋅
4 5
=4 ⋅ 8 − 5 ⋅ 7 =−3;
7 8
1 2
1 2
A33 =
= −3.
A23 =
6;
−
=
4 5
7 8
1 3
= −21;
7 0
1 3
A32 =
−
=
6;
4 6
−48 24 −3
3) A (=
=
Aij )T 42 −21 6 matritsani yozamiz.
−3
6 −3
4) A−1 matritsani topamiz:
16
− 9
−48 24 −3
1
1
14
−1
A =
⋅A=
⋅ 42 −21 6 =
det( A)
27
9
3
6
3
−
−
− 1
9
16
− 9
−1 14
Demak,
A
=
9
1
−
9
8
9
7
−
9
2
9
1
−
9
2
.
9
1
−
9
44
8
9
7
−
9
2
9
1
−
9
2
.
9
1
−
9

45.

A.I.Sotvoldiyev, Sh.Sh.Omonov
2. Teskari matritsani topishning Gauss-Jordan usulida xosmas matritsani shu
tartibdagi birlik matritsa bilan kengaytiriladi, kengaytirilgan matritsa satrlari ustida
elementar almashtirish to kengaytirilgan matritsa birinchi qismida birlik matritsa
hosil boʻlguncha olib boriladi, natijada kengaytirilgan matritsaning ikkinchi
qismida berilgan matritsaga teskari boʻlgan matritsa hosil boʻladi. Bu jarayonni
Gauss-Jordan modifikatsiyasi (yoki formulasi) koʻrinishida yozishimiz mumkin:
( A | E ) ~ ( E | A−1 )
1 1 1
Misol.
=
A 1 2 −1 matritsaga teskari matritsani Gauss-Jordan usulida
2 2 4
toping.
Yechish: 3 × 6 o‘lchovli ( A | E ) kengaytirilgan matritsani yozamiz va
matritsaning satrlari ustida elementar almashtirishlar bajarib, uni ( E | A−1 )
ko‘rinishga keltiramiz:
1 1 1 1 0 0
1 1 1 1 0 0
1 1 1 1 0 0
1 2 −1 0 1 0 ⇒ 0 1 −2 −1 1 0 ⇒ 0 1 0 −3 1 1 ⇒
2 2 4 0 0 1
0 0 2 −2 0 1
0 0 2 −2 0 1
1 1 1 1 0 0
1 0 0 5 −1 −1,5
⇒ 0 1 0 −3 1 1 ⇒ 0 1 0 −3 1
1 .
0 0 1 −1 0 0,5
0 0 1 −1 0 0,5
5 −1 −1,5
Demak, A−1 = −3 1
1 .
−1 0 0,5
_________________________________________________________
45

46.

A.I.Sotvoldiyev, Sh.Sh.Omonov
8-NAZORAT TOPSHIRIQLARI
Quyidagi matritsalarga teskari matrisalarni toping:
a) Klassik usulda;
b) Gauss-Jordan usulida.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
1 1
1 3
A2 2 −1
A1 =
, =
0 2
1 −1
1 2
7 2
A1 =
, A2 = −1 1
3 1
3 2
1
1
2
1 1 1
B2 = 5 4 3
10 5 1
1 2 1
0 2
=
B1 =
, B2 2 1 −1
−1 0
1 3 −1
3 −2
B1 =
,
5 −4
3
2
−1
1
3 1
B2 3
B1 =
, =
2 −4
0
1
2 5
B1 =
, B2 = 4
−1 1
7
0 1 3
1 −2
=
A1 =
, A2 2 0 −1
3 5
4 1 0
1 2 3
2 5
=
A1 =
, A2 3 2 −1
3 1
−1 0 1
1 −2 −1
3 2
A1 =
, A2 = 3 1 2
2 1
1 2 2
2 −1
−2 1
1 −2
2 3
5 6
8 9
2 1 1
B2 = 0 2 1
3 1 2
1 2 2
2 1
=
B1 =
, B2 2 1 −2
−3 0
2 −2 1
3 4
B1 =
,
2 5
4 5 −5
A2 = 1 2 2
5 7 −2
2 5 7
1 2
A1 =
, A2 = 6 3 4
3 4
5 −2 −3
6 2 −3
−1 2
=
A1 =
, A2 6 3 −2
3 −4
7 3 −3
2 3
A1 =
,
−1 4
3 −4 5
3 4
B2 2 −3 1
B1 =
, =
5 7
3 −5 −1
2 −8 −1
−12 −3
B2 4 −6 0
B1 =
, =
−7 −2
1 −5 −1
−1 −2 1
4 −2 5
A2 =−
8 −2 2
3 −6 9
3 3
A2 0 −3 6
A1 =
,=
−1 5
−1 2 5
0 0 4
B2 =−
3 −6 1
−5 −1 1
3 3 −1
−1 2
=
B1 =
, B2 5 1 −2
−3 3
4 1 1
1 −3
A1 =
,
3 −1
5 0
B1 =
,
−3 6
46

47.

A.I.Sotvoldiyev, Sh.Sh.Omonov
11.
−1 2
A1 =
,
2 3
12.
5 −2
A1 =
,
4
1
13.
2 −4
A1 =
,
2 −5
14.
−2 4
A1 =
,
1 1
15.
16.
17.
18.
19.
20.
21.
1 −1 0
A2 =−
2 −1 4
8 −1 −1
0 2 −4
A2 = 1 2 2
6 2 4
2 3 2
B2 = −1 −3 −1
−3 −1 −3
−4 3 0
−3 −7
B1 =
, B2 = 0 1 2
−5 0
−2 4 −2
6 −8
B1 =
,
1 0
7
A2 = 7
8
0
A2 = 1
1
0 2
1 3
−1 2
3 −6
3 2
3 3
2 2 7
B2 = 0 0 6
−2 5 7
−1 2 3
3 −1
=
B1 =
, B2 0 1 −2
1 5
−3 4 −1
2
1 −2
A2 4
A1 =
, =
2 −5
2
1
0 1
A2 2
A1 =
, =
−3 9
1
−1 3
−2 5
−1 1
−2 3
−4 5
−2 1
1 2 1
1 1
=
B1 =
, B2 0 1 −1
−1 −2
2 5 4
2 −4 1
7 −3
B2 1 −5 3
B1 =
, =
−8 4
1 −1 1
1 2 1
3 5
=
A1 =
, A2 0 1 −1
4 7
2 5 1
1 1 −1
−4 5
A1 =
, A2 3 4 −1
=
−6 8
4 1 −2
1 4 3
1 0
=
B1 =
, B2 0 1 −1
−6 2
0 9 5
1 −2 −1
7 −2
B1 =
, B2 = 0 2 1
10 −3
1 1 −1
−1 0 1
6 −4
A2 3 −1 2
A1 =
,=
3 2
0 1 5
−1 7 0
0 −3
A1 =
, A2 = 0 3 1
−5 12
1 −1 2
−1 2 1
B2 = 1 1 4
−1 0 2
1 2 1
4 −2
B2 1 −3 5
B1 =
, =
3 −5
4 2 0
3 −2
A1 =
,
5
−
4
3 1
B1 =
,
−7 −4
1 −1
B1 =
,
−1 1
−1 5 6
A2 = 0 5 1
3 2 −1
−9 1
B1 =
,
10
−
1
47
2 1 0
B2 = 1 0 1
4 2 1

48.

A.I.Sotvoldiyev, Sh.Sh.Omonov
22.
23.
24.
−1 2
A1 =
,
6 −10
25.
0 −1
A1 =
,
3 −11
26.
27.
−9 −8 −3
B2 = 1 4 1
−3 2 0
3 1 8
1 −6
=
B1 =
, B2 1 2 −1
0 2
0 1 3
1 1 2
0 5
=
A1 =
, A2 1 2 −1
4 −9
3 0 2
2 −1 −3
0 7
A1 =
, A2 = 2 1 0
−1 5
1 −1 0
−1 −3 −3
A2 = 1 0 2
−1 0 5
1 −2 −1
A2 = 0 2 1
1 1 −1
2
10 11
A2 1
A1 =
, =
12 13
4
1
4 2
A1 =
, A2 =−
4
9 5
6
28.
9
2
A1 =
,
−3 −15
29.
−1 −6
A1 =
,
−
1
−
7
30.
7 −5
A1 =
,
−3 2
2 7
B1 =
,
6 19
1 4
−1 3
1 5
2 3
−6 2
1 5
7 −5
B1 =
,
−3 2
4 5
B1 =
,
6 7
0 1 0
B2 = 7 5 3
−2 0 1
2 0 1
−1 2 −1
B2 =
1 1 3
3 −5
B2 = 4 6
7 2
4 3
0 1
B1 =
, B2 = 1 −1
3 −8
0 1
0
1
1
2 1
B2 = 1 1
−1 2
−2 1
9 1
B2 1 −3
B1 =
,=
−2 0
−1 0
1
4
0
7 8
B1 =
,
9
10
1 −2 3
A2 = 5 1 4
−2 0 1
1 0 3
A2 = 0 1 2
3 1 4
3 1
B1 =
,
−2 −1
2
−2
2
0
2
1
1 2 −1
6 −8
B2 2 −3 1
B1 =
, =
4 −5
0 2 4
0 1 5
A2 = −1 2 3
1 2 4
48