2.1 лекция. Целые и рациональные числа. Действительные числа. Комплексные числа

1.

ТЕМА:
Целые и рациональные числа.
Действительные числа.
Комплексные числа.
Приближенные вычисления

2. Содержание:

СОДЕРЖАНИЕ:
1. Натуральные числа.
2. Целые числа.
3. Рациональные числа
4. Действительные числа
5. Преобразование выражений с
действительными числами.
6. Комплексные числа. Вычисления

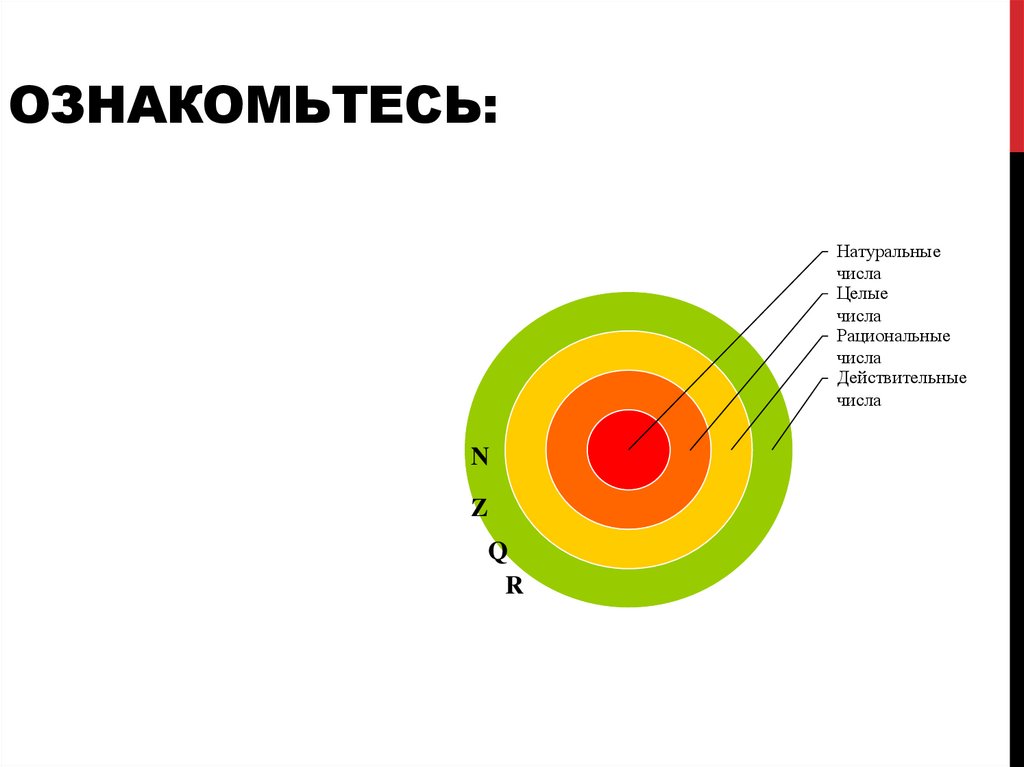
3. Ознакомьтесь:

ОЗНАКОМЬТЕСЬ:
Натуральные
числа
Целые
числа
Рациональные
числа
Действительные
числа
N
Z
Q
R

4.

Для счета предметов используются числа , которые
называются натуральными. Для обозначения
множества натуральных чисел употребляется
буква N -первая буква латинского слова Naturalis,
«естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z - первой буквой
немецкого слова Zahl - «число».

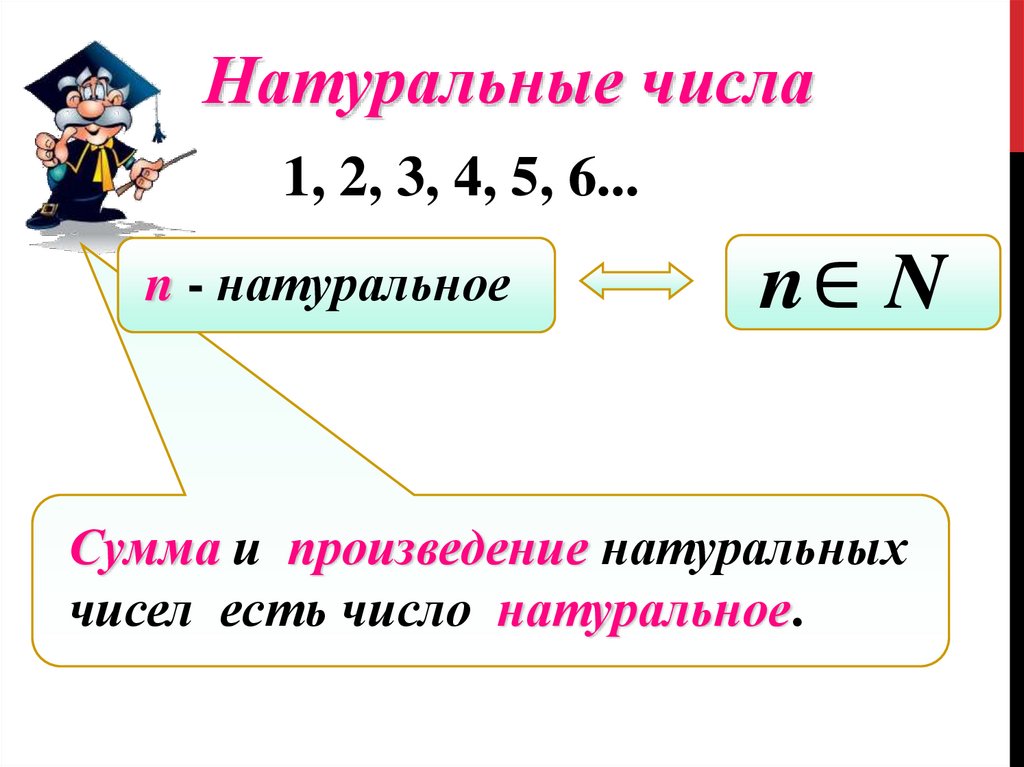
5.

Натуральные числа
1, 2, 3, 4, 5, 6...
n - натуральное
n∈ N
Сумма и произведение натуральных
чисел есть число натуральное.

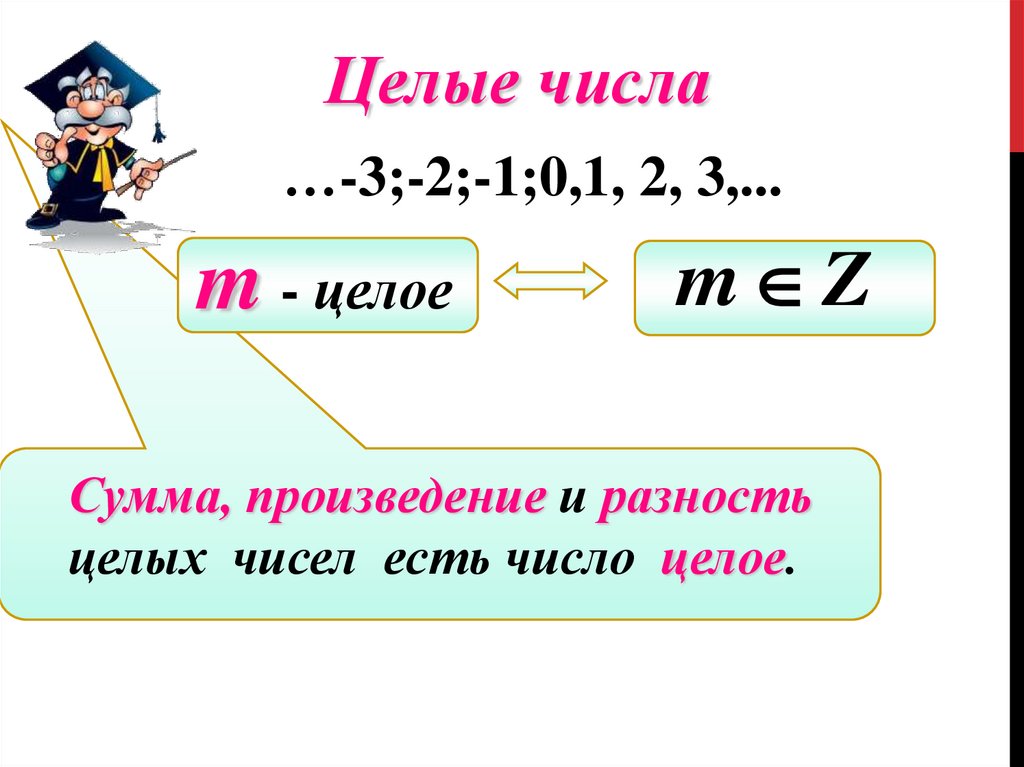
6. Целые числа

ЦЕЛЫЕ ЧИСЛА
Целыми числами называют множество
натуральных чисел, им противоположных и число
нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны суммы,
произведения и разности.

7.

Целые числа
…-3;-2;-1;0,1, 2, 3,...
m - целое
m Z
Сумма, произведение и разность
целых чисел есть число целое.

8.

Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)его работа была обнаружена в 1848
году.

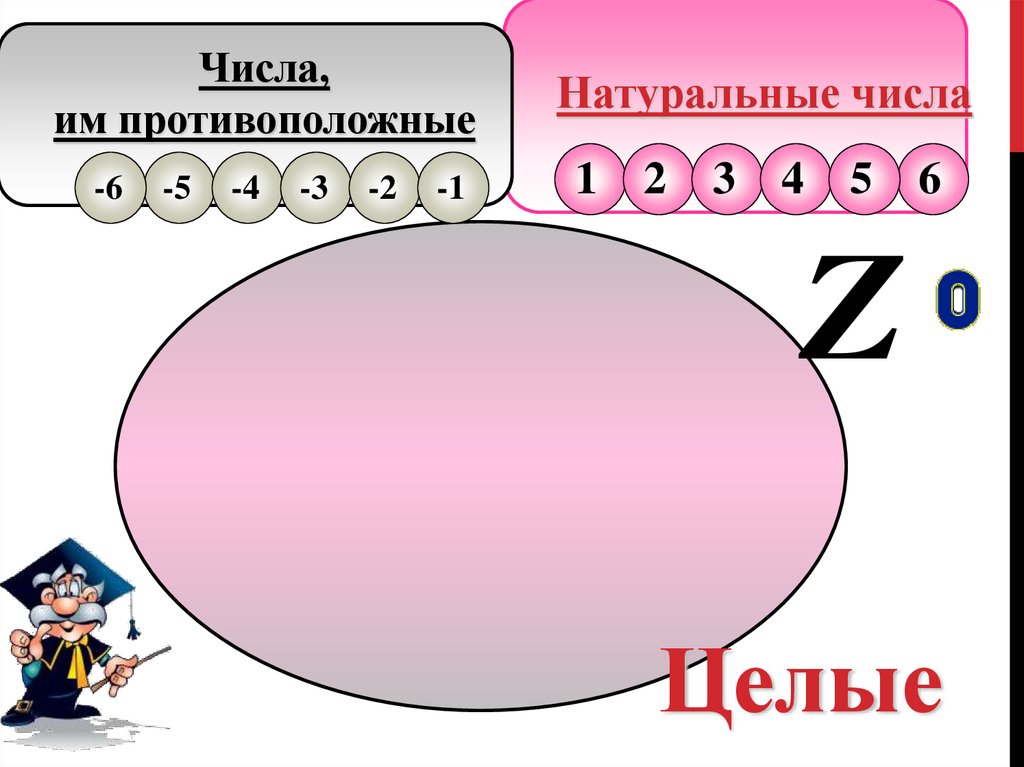
9.

Числа,
им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые

10.

m
Множество чисел, которое можно представить в виде
,
n
называется множеством рациональных чисел и
обозначается- Q первой буквой французского слова Quotient
- «отношение».

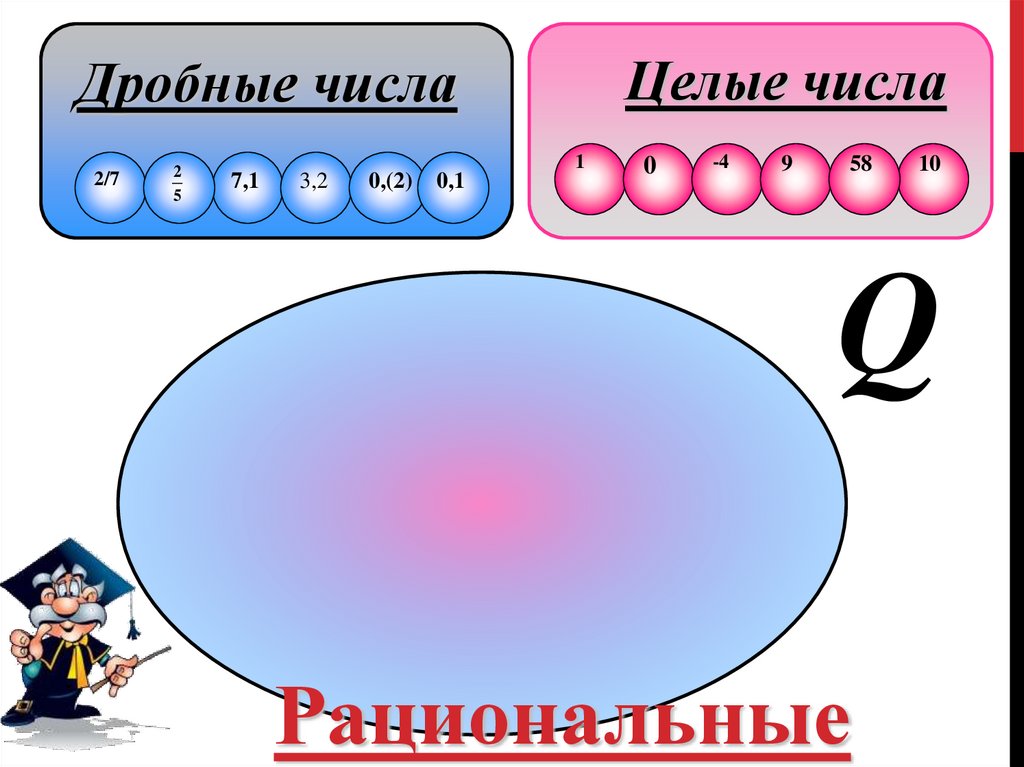
11. Рациональные числа

РАЦИОНАЛЬНЫЕ ЧИСЛА
Целые и дробные числа составляют множество
рациональных чисел.
Q=(целые числа, дробные числа)
Рациональные числа замкнуты относительно суммы,
разности, произведения и частного (исключая деления на
нуль)

12.

Рациональное число (лат. ratio —
отношение, деление, дробь) — число,
представляемое обыкновенной дробью , где
числитель m — целое число, а знаменатель
n — натуральное число. Такую дробь
следует понимать как результат деления m
на n, даже если нацело разделить не
удаётся. В реальной жизни рациональные
числа используются для счёта частей
некоторых целых, но делимых объектов,
например, тортов или других продуктов,
разрезаемых на несколько частей

13.

Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные

14.

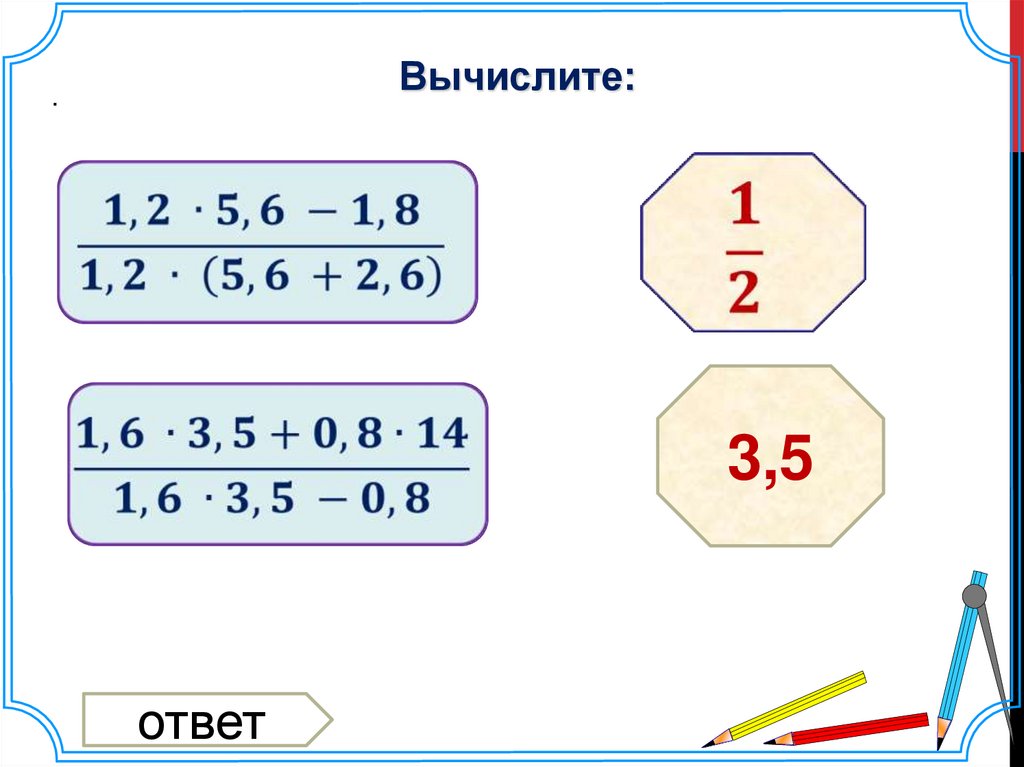
Выполнить действия
Ответы

15.

Вычислите:
.
3,5
ответ

16.

Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.

17.

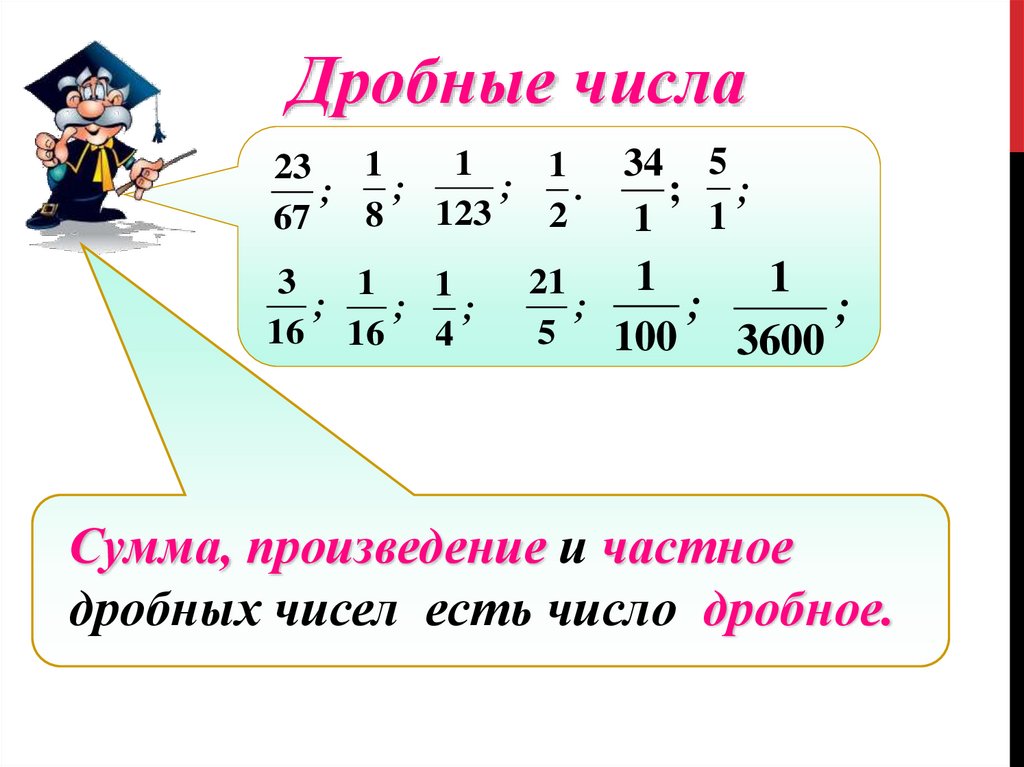
Дробные числа
1
1
23 1
;
;
.
;
8 123
2
67
3
1
1
;
;
;
16 16 4
34 5
; ;
1 1
1
21
;
;
5
100
1
;
3600
Сумма, произведение и частное
дробных чисел есть число дробное.

18.

Десятичные дроби в XV веке
ввел самаркандский ученый
ал - Хорезми.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).

19.

Множество рациональных чисел
Множество рациональных чисел обозначается и может
быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби
такие как, например, 3/4 и 9/12 , входят в это множество
как одно число.
Поскольку делением числителя и знаменателя дроби на их
наибольший общий делитель можно получить
единственное несократимое представление рационального
числа, то можно говорить об их множестве как о множестве
несократимых дробей со взаимно простыми целым
числителем и натуральным знаменателем:

20.

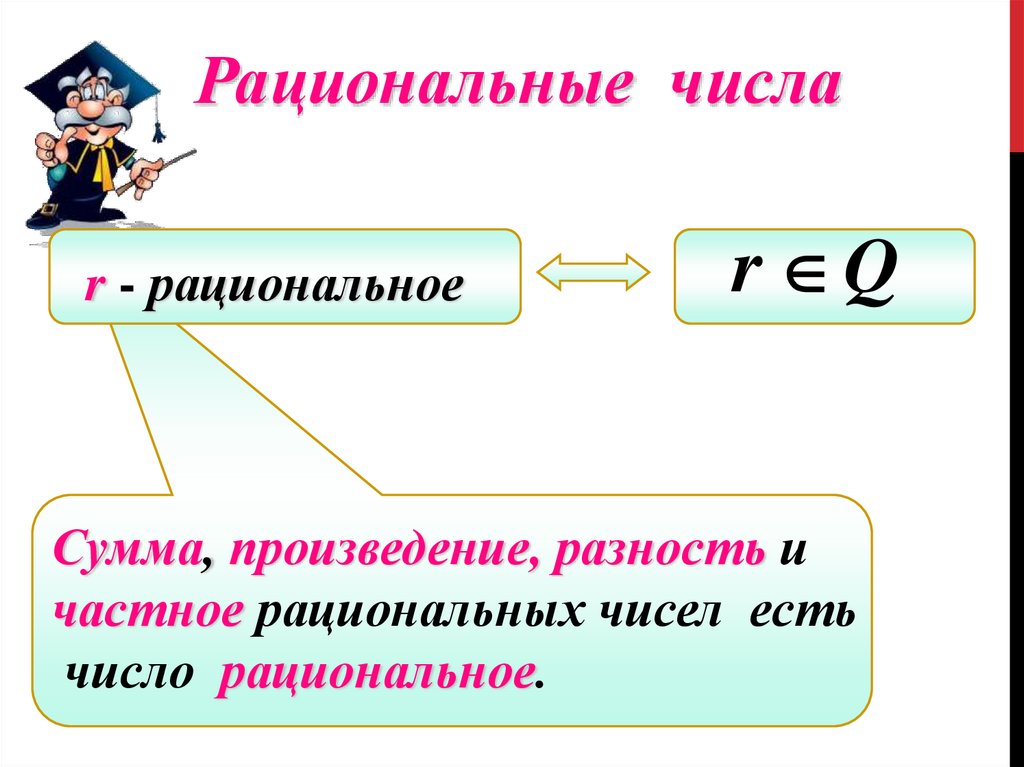
Рациональные числа
r - рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.

21.

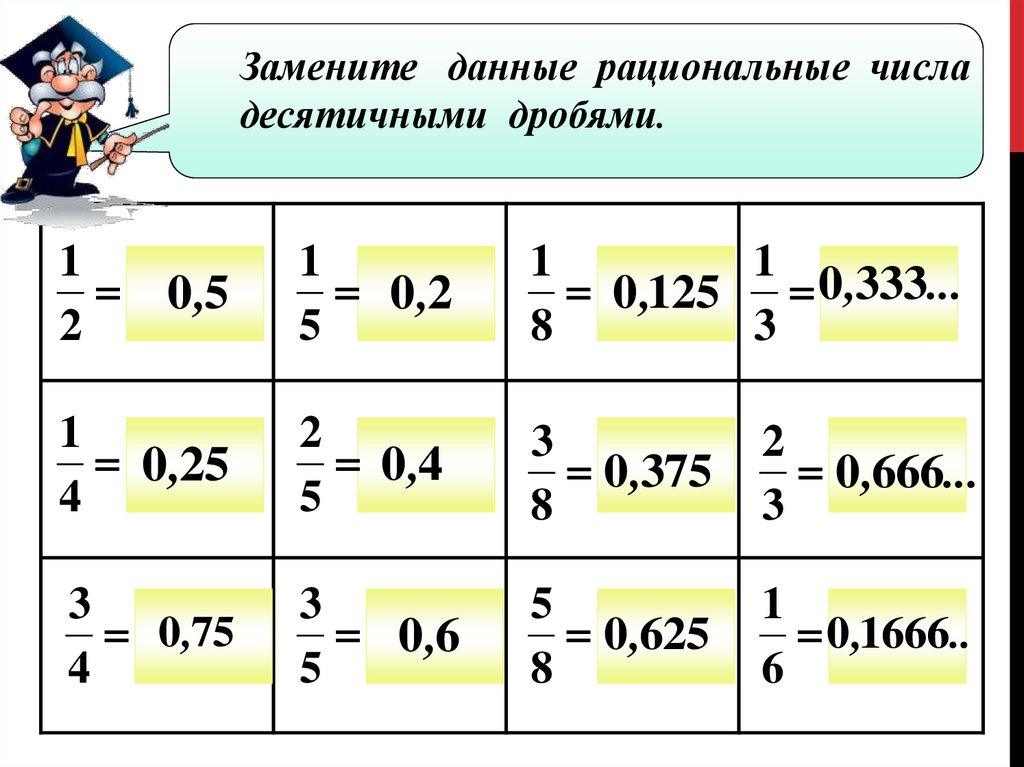
Замените данные рациональные числа
десятичными дробями.
1
2
0,5
1
0,2
5
1
1
0,125
0 ,333...
8
3
1
0,25
4
2
0,4
5
3
0,375
8
2
0 ,666...
3
3
0,75
4
3
0,6
5
5
0,625
8
1
0 ,1666..
6

22.

Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
1 цифра
9
0,(81)=
81
2 цифры
99
9
11

23.

Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного
цифрами, стоящими после запятой до начала второго
периода, и числа, образованного из цифр, стоящих после
запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько
цифр в периоде, и со столькими нулями, сколько цифр
между запятой и началом периода.
0,4(6)=
46
1 цифра
1 цифра
90
42 7
90 15

24. Рациональные числа как бесконечные десятичные дроби

РАЦИОНАЛЬНЫЕ ЧИСЛА КАК
БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ
ДРОБИ
Для всех рациональных чисел можно использовать один и
тот же способ записи. Рассмотрим
1. Целое число 5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)

25. Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.

ПРИМЕР. ЗАПИСАТЬ В ВИДЕ ОБЫКНОВЕННОЙ
ДРОБИ БЕСКОНЕЧНУЮ ДЕСЯТИЧНУЮ
ПЕРИОДИЧЕСКУЮ ДРОБЬ.
Положим, что х=1,(23), т.е. 1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
Итак: 1,(23)=
122
99

26.

Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё на 100
1000х=1523,2323…
10х= 5,232323…
990х=1508
х=
Итак: 1,5(23)=
1508
999
1508
999

27. Иррациональные числа

ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
Бесконечная
непериодическая дробь
называется иррациональным
числом.
Например:
Множество иррациональных чисел
обоначается J.

28. Действительные числа

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
R=(рациональные числа, иррациональные числа)
Действительные числа не обладают свойством замкнутости не всякое уравнение имеет корни.

29. ОСНОВНЫЕ ПОНЯТИЯ

Комплексным числом z называют выражение:
z a i b,
где а и b – действительные числа, i – мнимая единица,
определяемая равенством:
i
1
i 2 1
а - называется действительной частью числа z,
b – мнимой частью. Их обозначают так:
a Re z;
b Im z.
Если а = 0, то число i b называется чисто мнимым.
Если b = 0, то получается действительное число а.
Два комплексных числа, отличающиеся только знаком мнимой части,
называются сопряженными:
z a i b,
z a i b,

30. Геометрическое изображение комплексных чисел

ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ
КОМПЛЕКСНЫХ ЧИСЕЛ
z a i b,можно изобразить на плоскости
XOY в виде точки A(a; b).
Всякое комплексное число
Плоскость, на которой изображаются комплексные числа,
называют плоскостью комплексной переменной.
y
z
b
A(a; b)
Точкам, лежащим на оси OX, соответствуют
действительные числа (b = 0), поэтому
ось OX называют действительной осью.
0
a
х
Точкам, лежащим на оси OY , соответствуют чисто мнимые числа
(a = 0), поэтому ось OY называют мнимой осью.
Иногда удобно считать геометрическим изображением комплексного
числа z вектор
OA

31. Тригонометрическая форма записи комплексных чисел

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНЫХ ЧИСЕЛ
Обозначим через r модуль вектора OA, через φ угол между вектором OA
и положительным направлением оси OX.
Тогда имеют место равенства:
y
z
A(a; b)
b
r
0
a r cos ;
b r sin
Следовательно, комплексное число z можно
представить в виде:
φ
a
х
a i b r cos i r sin
z r (cos i sin )
b
Модуль
комплексного
Аргумент
2комплексного
2
Тригонометрическая
arg z arctg
r zчисла
aчисла
b
форма записи
a
комплексного
числачисла z считается положительным, если он
Аргумент
комплексного
отсчитывается от положительного направления оси OX против часовой
стрелки. Очевидно, что φ определяется не однозначно, а с точностью до
слагаемого
2 k k Z.

32. Действия над комплексными числами

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
1
Равенство комплексных чисел.
Два комплексных числа z1 a1 i b1 и z2 a2 i b2 называются
равными : z1 z,2если a a , b b
1
2
1
2
Комплексное число z a i b равно нулю , тогда и только тогда,
когда a 0, b 0
2
Сложение и вычитание комплексных чисел.
Суммой (разностью) комплексных чисел z1 a1 i b1 и
z2 a2 i b2 называется комплексное число, определяемое
равенством:
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2

33. Действия над комплексными числами

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
Сложение и вычитание комплексных
чисел, изображенных векторами
производится по правилу сложения или
вычитания векторов:
y
z
z1 + z2
z1
z1 - z2
z2
0
3
х
Умножение комплексных чисел.
Умножением комплексных чисел z1 a1 i b1 и
z2 a2 i b2
называется число, получаемое при умножении этих чисел по правилам
алгебры как двучлены, учитывая что
i 2 1;
i 3 i ;
i 4 i i 1;
i5 i
i 4k 2 1;
i 4k 3 i
При любом целом k:
i 4k 1;
i 4k 1 i ;

34. Действия над комплексными числами

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
На основании этого правила получим:
z1 z2 a1 i b1 a2 i b2
a1 a2 i b1 a2 i b2 a1 i 2 b1 b2
z1 z2 a1 a2 b1 b2 i b1 a2 b2 a1
Если комплексные числа заданы в тригонометрической форме:
z1 r1(cos 1 i sin 1 ) z2 r2 (cos 2 i sin 2 )
тогда произведение находится по формуле:
z1 z2 r1 r2 (cos( 1 2 ) i sin( 1 2 ))
Произведение сопряженных комплексных чисел:
z z (a i b ) (a i b ) a 2 (i b)2 a 2 b 2
z z a b z
2
2
2

35. Действия над комплексными числами

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
4
Деление комплексных чисел.
Чтобы разделить z a i b на
z2 a2 i b2
1
1
1
необходимо умножить делимое и делитель на число, сопряженное
делителю:
z1 a1 i b1
(a1 i b1 ) (a2 i b2 )
z2 a2 i b2 (a2 i b2 ) (a2 i b2 )
(a1a2 b1b2 ) i (a2b1 a1b2 ) a1a2 b1b2
a2b1 a1b2
i
2
2
2
2
a2 b2
a2 b2
a22 b22
Если комплексные числа заданы в тригонометрической форме:
z1 r1(cos 1 i sin 1 )
z2 r2 (cos 2 i sin 2 )
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z2 r2

36. Действия над комплексными числами

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ
ЧИСЛАМИ
Найти произведение и частное комплексных чисел:
z1 2 3i,
z2 1 4i
= -1
z1 z2 2 3i 1 4i 2 3i 8i 12i 2
2 3i 8i 12 14 5i
z1 2 3i
(2 3i ) (1 4i ) 2 3i 8i 12i 2
2
2
z2 1 4 i
(1 4i ) (1 4i )
1 4
10 11
10 11i
2 3i 8i 12
i
17 17
17
17

37. Задания для самопроверки

ЗАДАНИЯ ДЛЯ
САМОПРОВЕРКИ
• Какие дроби называются десятичными
• Действия с обыкновенными и десятичными дробями
• Какие числа называются действительными?
• Действия с действительными числами.
•Какое число называется комплексным?

38.

Проверь себя
72
8
8
1) 1, (72) 1
1 1
99
11
11
912 9
903
301
2) 2,9(12) 2
2
2
990
990
495
128 12
116
29
3) 1,12(8) 1
1
1
900
900
225

39.

Самостоятельная работа
1. Записать в виде десятичной дроби
а)
5 б)
99
53
12
2.Представьте в виде обыкновенной дроби
а) 2,3(82)
б) 2,(14)
в) 1,6(1)