Разложение вектора по двум неколлинеарным векторам. Координаты вектора.
Разложение вектора по двум неколлинеарным векторам
Если векторы а и b коллинеарны и а  0, то существует такое число k, что b = ka
Любой вектор можно представить как результат сложения двух неколлинеарных векторов т. е. разложить по двум неколлинеарным
Чтобы разложить вектор по двум векторам надо: 1) отложить все три вектора от одной точки; 2) достроить до параллелограмма; 3)
Задание: разложите векторы x и y по векторам a и b
Координаты вектора
Координатные векторы i и j – единичные векторы (длина равна 1); i – по оси Ox, j – по оси Oy
Любой вектор можно разложить по координатным векторам
Коэффициенты разложения называются координатами вектора
Определите координаты вектора
Правила
Найдите координаты вектора р ⃗= а ⃗+b ⃗
Найдите координаты вектора р ⃗= а ⃗-b ⃗
Правила
р ⃗{4;-3} Найдите координаты векторов
а ⃗{"7; 2" }, b ⃗{"3; 5" }. Найдите с ⃗=3а ⃗-2b ⃗ . Составьте план
Выполните задание
0.98M
Similar presentations:
Метод координат на плоскости
Метод координат на плоскости
Метод координат. Координаты вектора
Метод координат. Координаты вектора
Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам. Координаты вектора. 9 класс
Разложение вектора по двум неколлинеарным векторам. Координаты вектора. 9 класс
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам
Метод координат на плоскости
Метод координат на плоскости
Векторы в пространстве. Урок 3-4
Векторы в пространстве. Урок 3-4
Разложение вектора по трем некомпланарным векторам
Разложение вектора по трем некомпланарным векторам

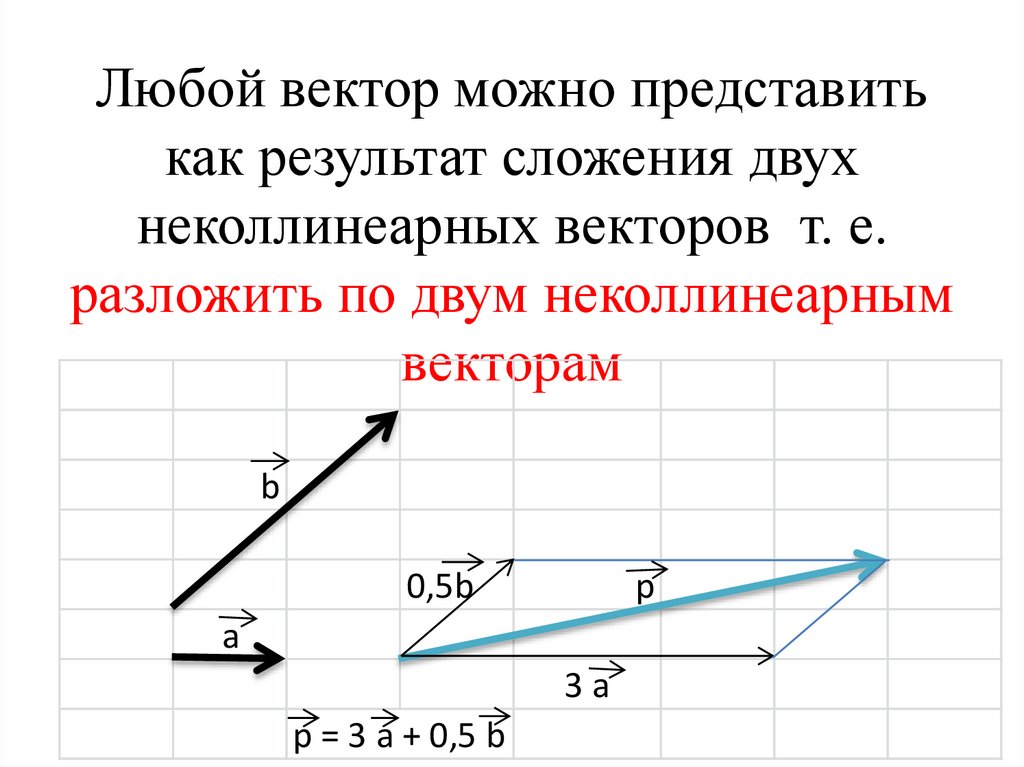
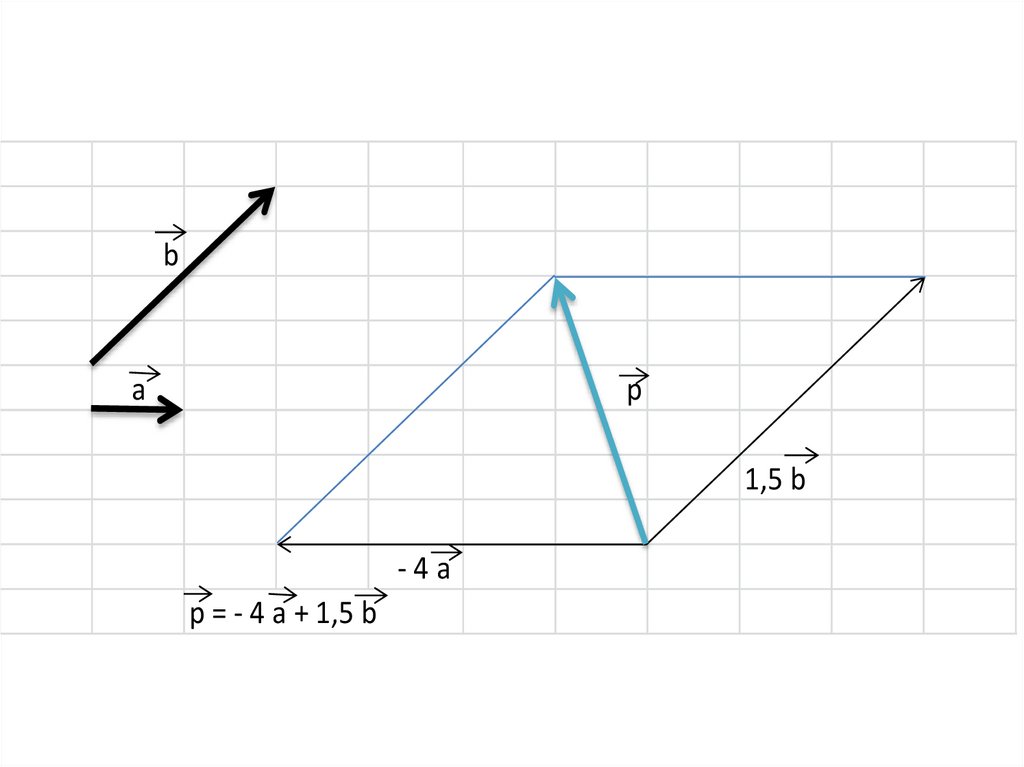
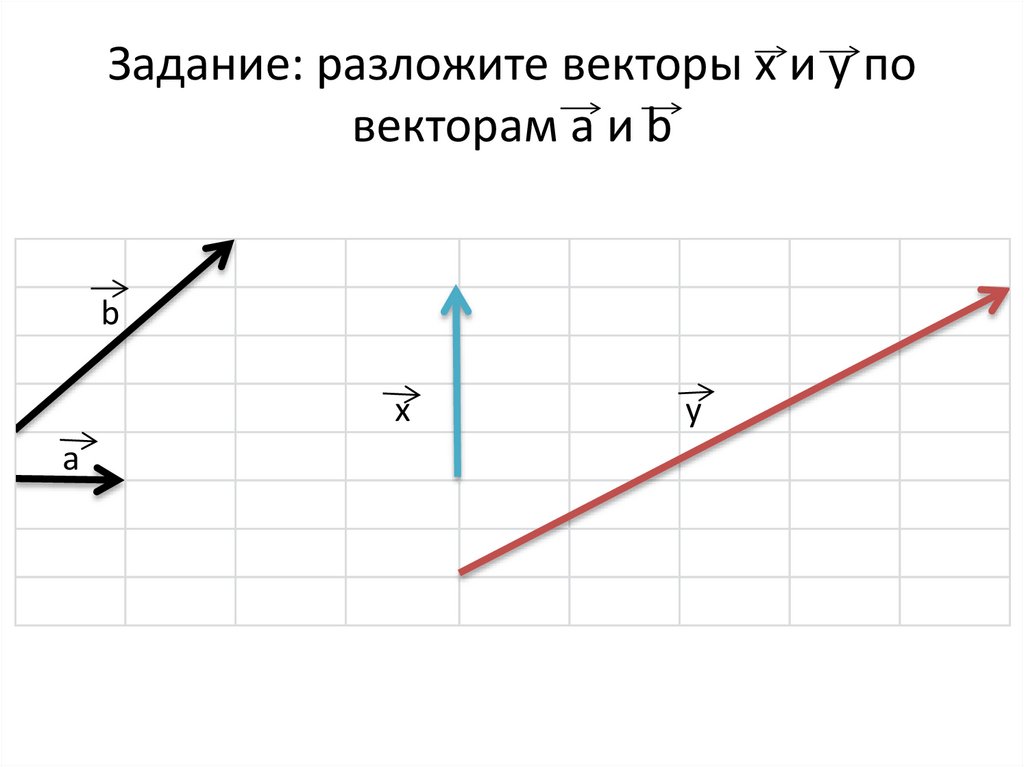
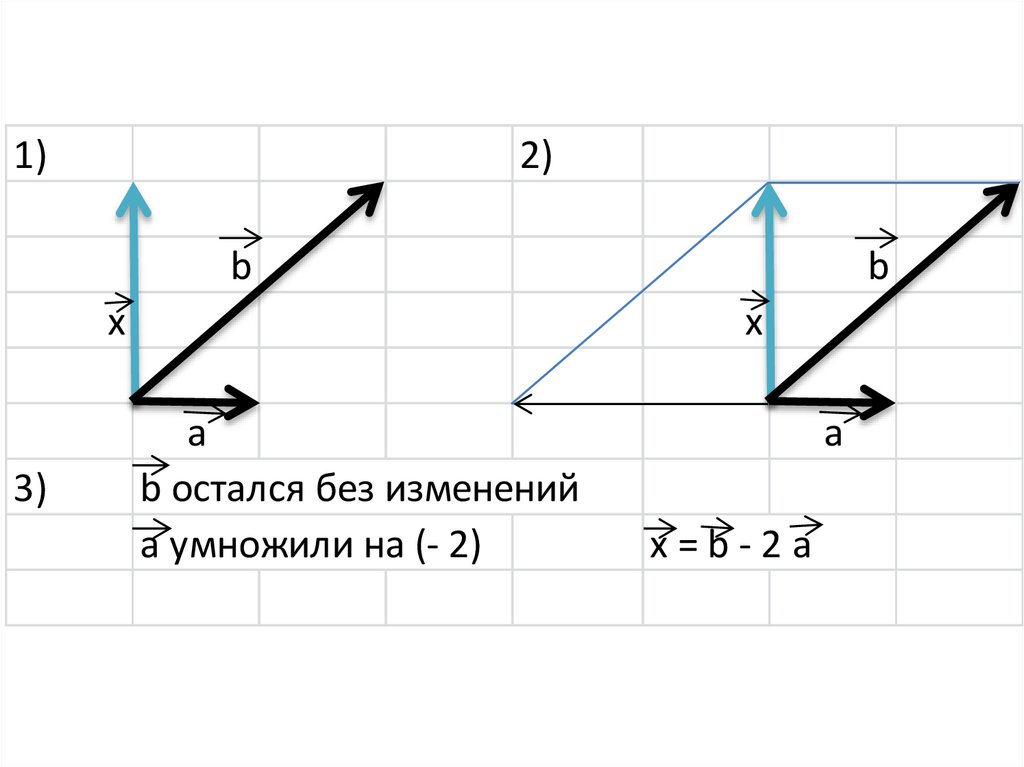
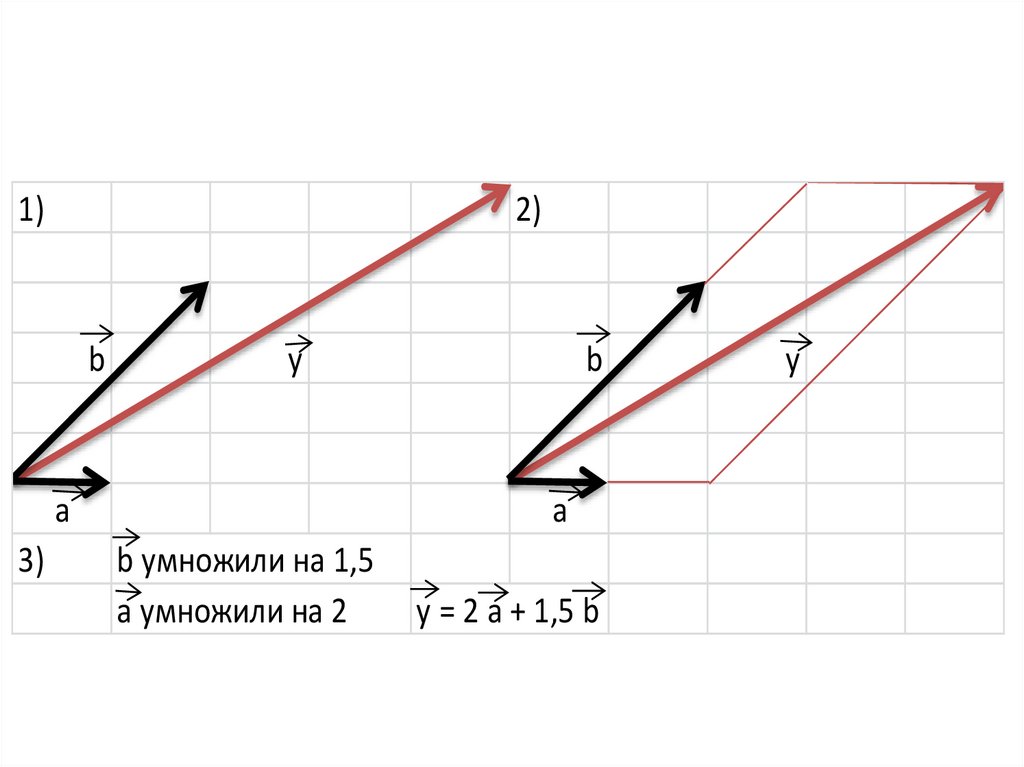
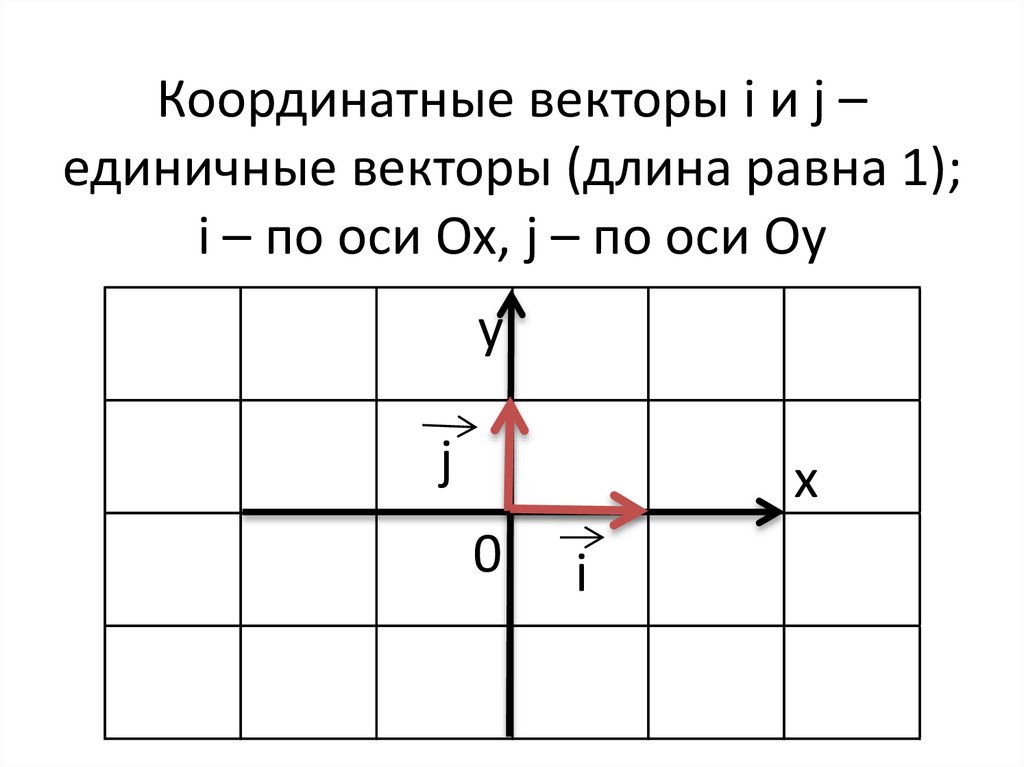
разложение вектора по двум неколлинеарным векторам

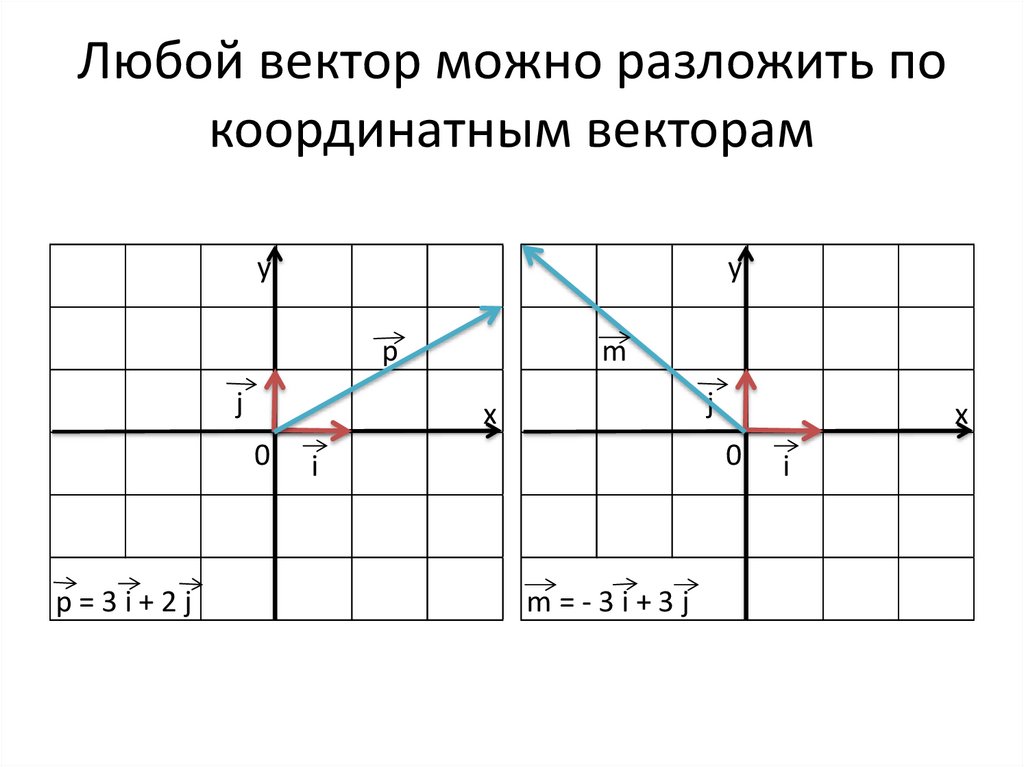
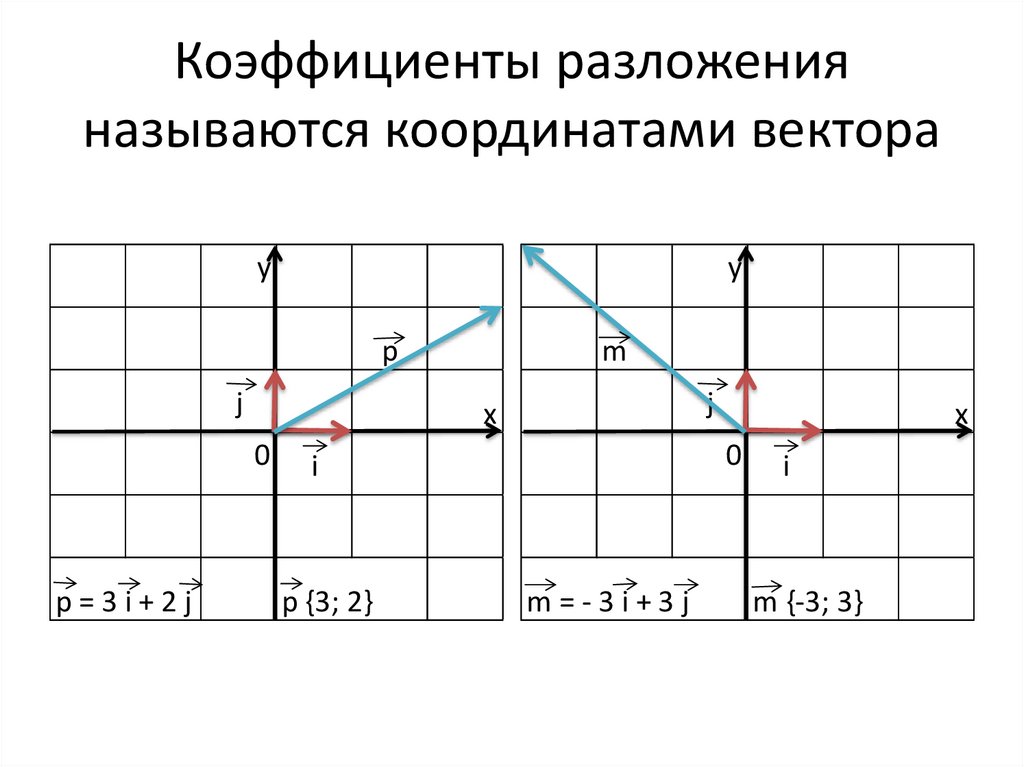
1. Разложение вектора по двум неколлинеарным векторам. Координаты вектора.

2. Разложение вектора по двум неколлинеарным векторам

3.

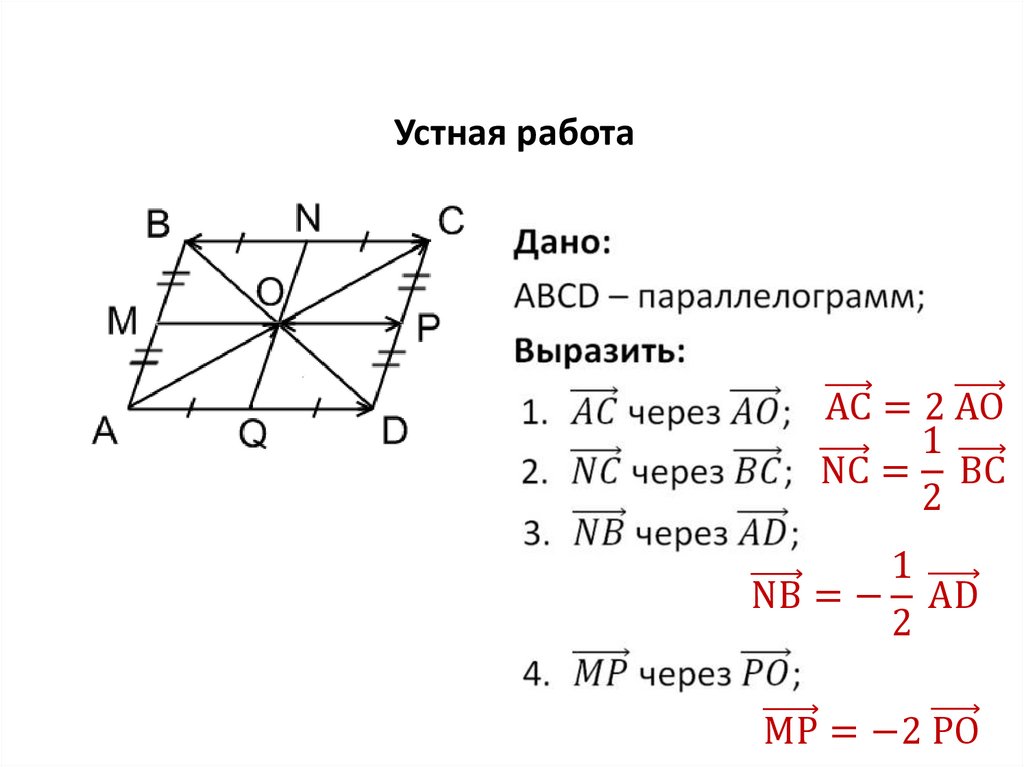
Устная работа
АС = 2 АО
1
NС = ВC
2
1
NВ = − АD
2
МР = −2 РО

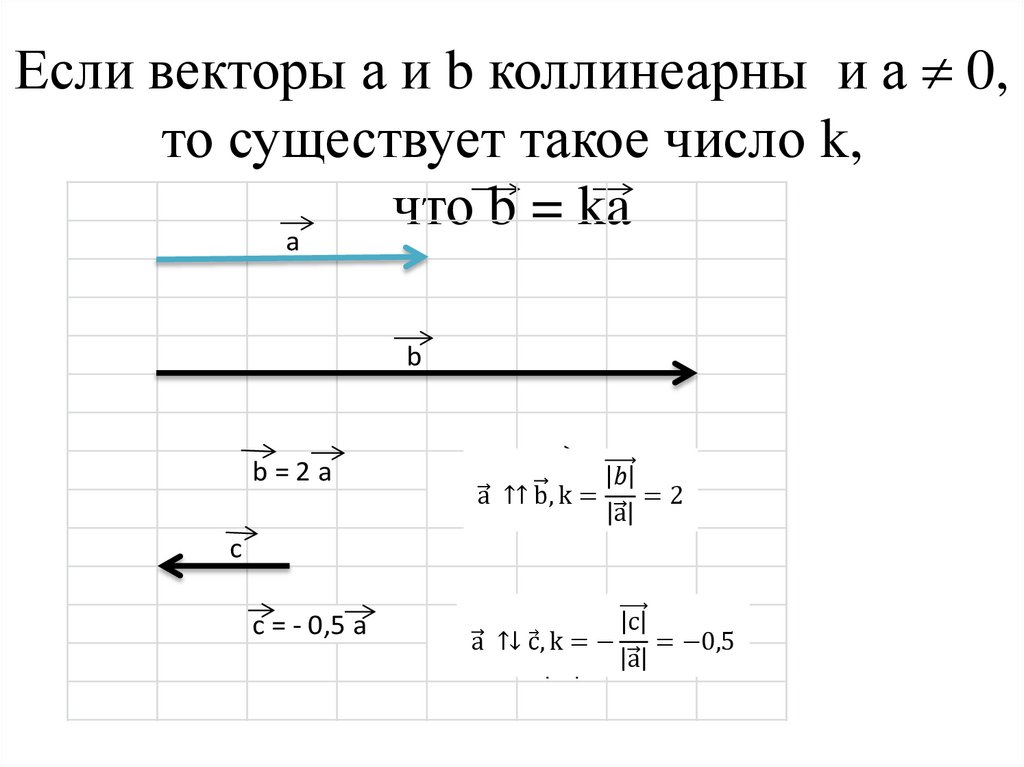
4. Если векторы а и b коллинеарны и а  0, то существует такое число k, что b = ka

Если векторы а и b коллинеарны и а 0,
то существует такое число k,
что
b
=
ka
а
b
b=2a
│b│
English     Русский Rules