Similar presentations:
Разложение вектора по двум неколлинеарным векторам. Координаты вектора
1.
Разложение вектора по двумнеколлинеарным векторам.
Координаты вектора.
9 класс
2.
Разложениевектора по двум
неколлинеарным
векторам
3.
Если векторы а и b коллинеарны иа 0, то существует такое число k,
что b = ka
а
b
b=2a
k=
│b│
=2
│a│
k=
│c│
= - 0,5
│a│
c
c = - 0,5 a
4.
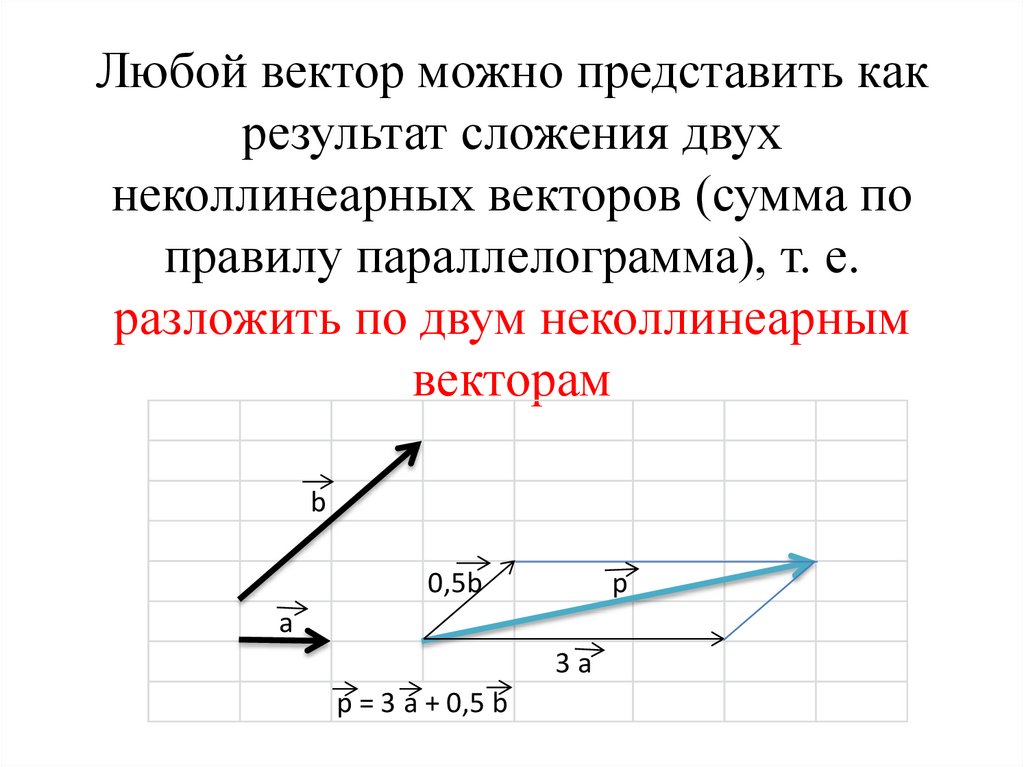
Любой вектор можно представить какрезультат сложения двух
неколлинеарных векторов (сумма по
правилу параллелограмма), т. е.
разложить по двум неколлинеарным
векторам
b
0,5b
p
a
3a
p = 3 a + 0,5 b
5.
ba
p
1,5 b
-4a
p = - 4 a + 1,5 b
6.
Чтобы разложить вектор по двумвекторам надо:
1) отложить все три вектора от
одной точки;
2) достроить до параллелограмма;
3) вычислить значения k для
каждого вектора
7.
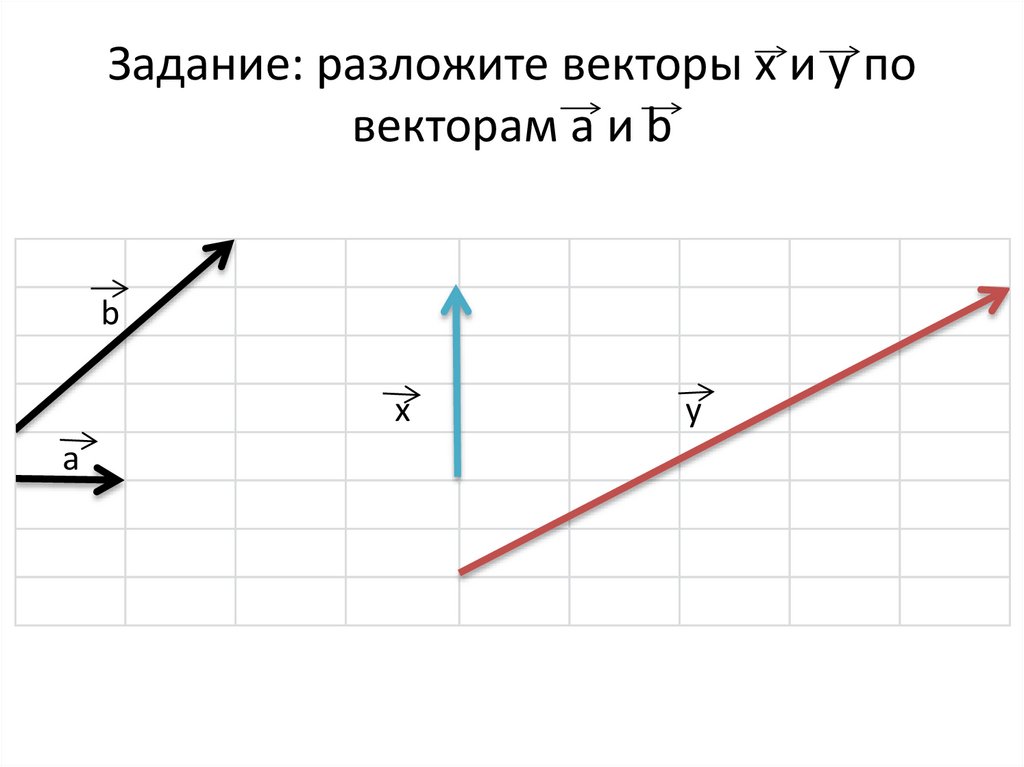
Задание: разложите векторы x и y повекторам a и b
b
x
a
y
8.
1)2)
b
x
3)
b
x
a
b остался без изменений
a умножили на (- 2)
a
x=b-2a
9.
2)1)
b
a
a
3)
b
y
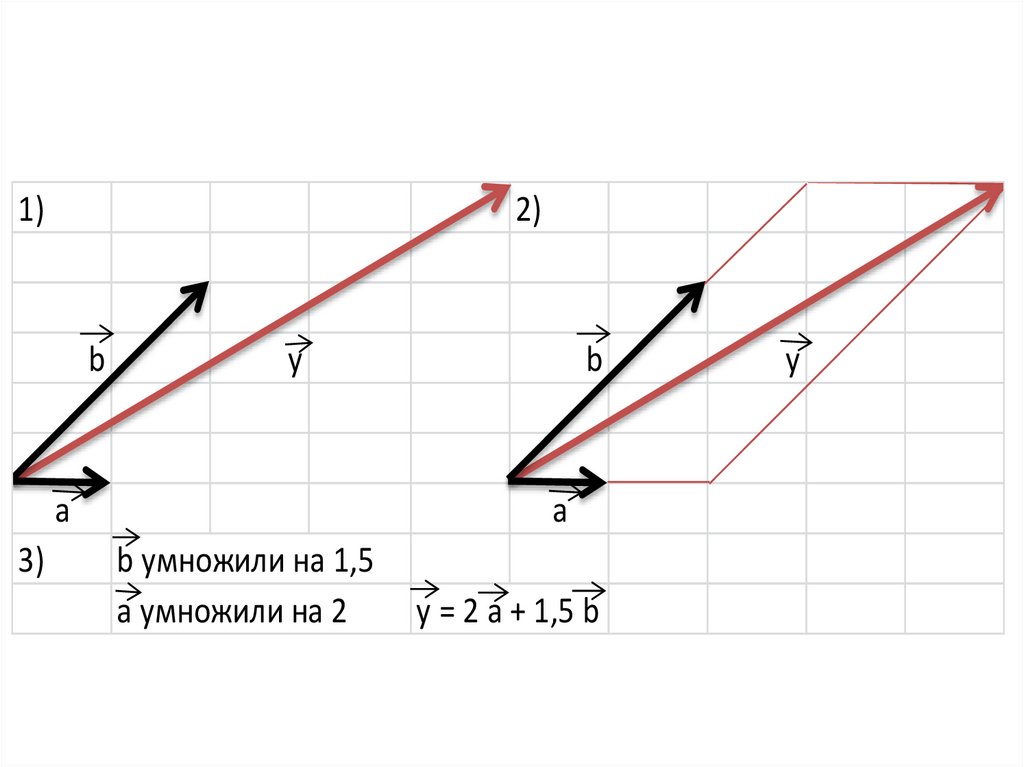
b умножили на 1,5
a умножили на 2
y = 2 a + 1,5 b
y
10.
Координатывектора
11.
YC 4
A
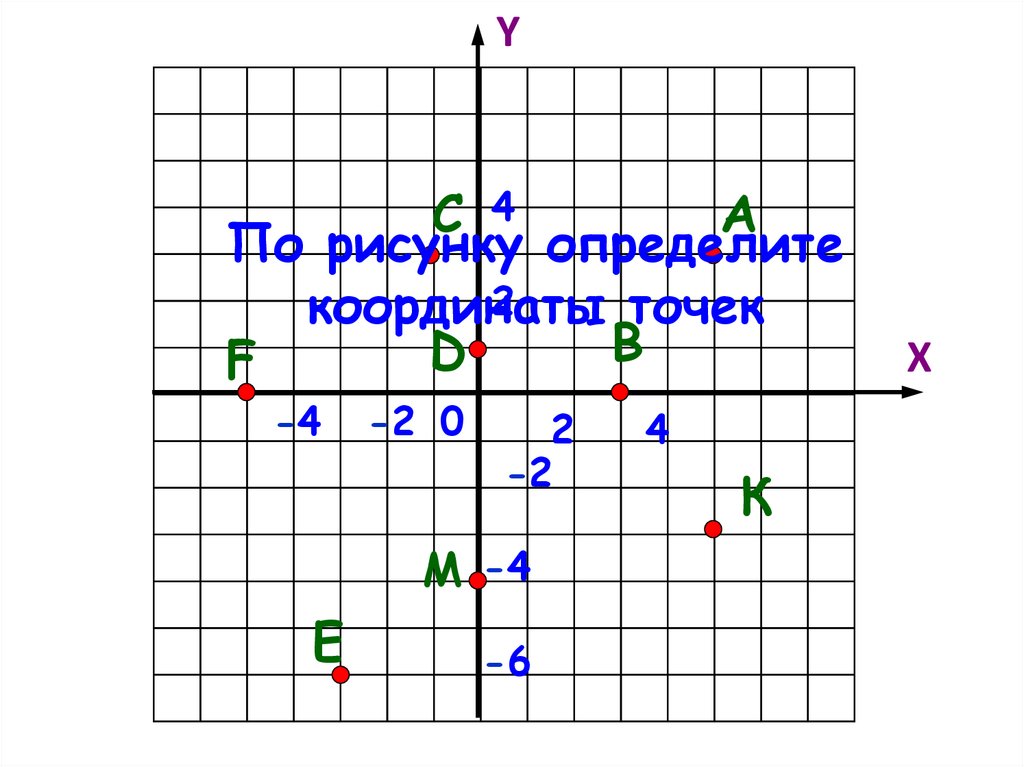
По рисунку определите
2
координаты
точек
B
D
F
-4
-2 0
2
-2
М -4
E
-6
4
К
X
12.
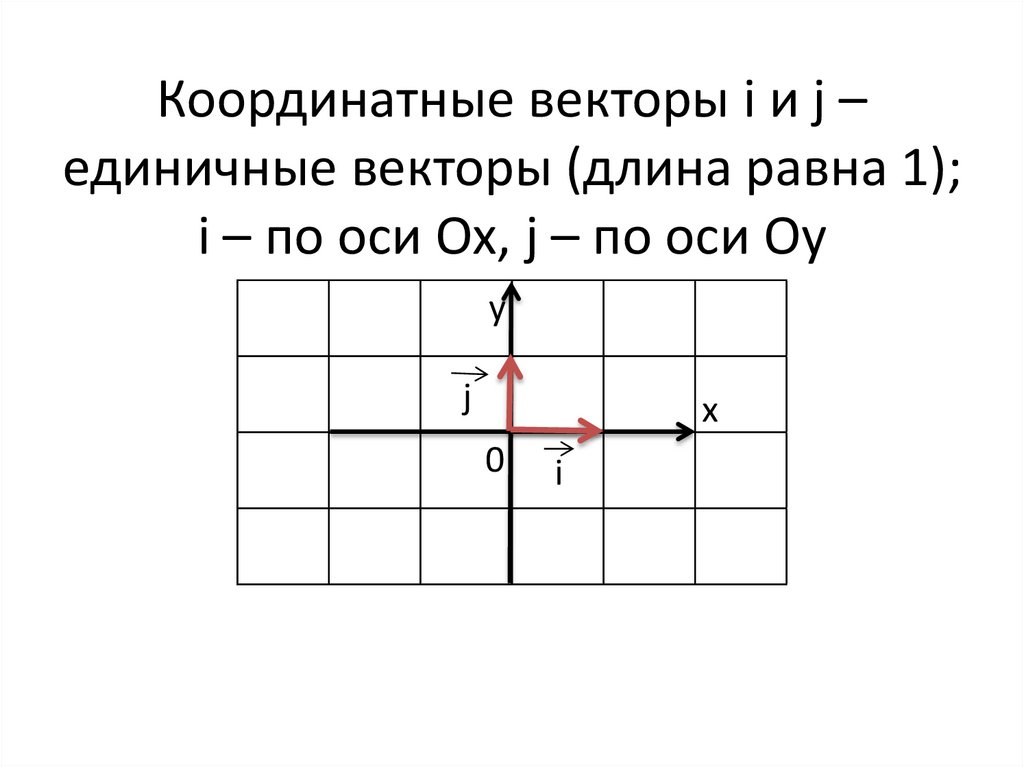
Координатные векторы i и j –единичные векторы (длина равна 1);
i – по оси Ox, j – по оси Oy
y
j
x
0
i
13.
Отложим от начала координат О единичные векторыi и j так, чтобы направление вектора j cовпало с
направлением оси Ox, а направление вектора j – с
направлением оси Oy. Векторы i и j назовем
координатными векторами.
Y
В
5i
ОА{3;2}
-3j
ВС{5;-3}
A
С
j
0
i
X
14.
Любой вектор можно разложить покоординатным векторам
y
y
p
j
j
x
0
p=3i+2j
m
x
0
i
m=-3i+3j
i
15.
Коэффициенты разложенияназываются координатами вектора
y
y
p
j
j
x
0
p=3i+2j
m
0
i
p {3; 2}
x
m=-3i+3j
i
m {-3; 3}
16.
Начертите прямоугольную системукоординат. Постройте векторы с началом
в точке О, заданные координатами a{4;0},
b{3;-2}, c{5;5}, d{-6;-3}, e{-4;1},
Y
c
e
d
a
b
X
17.
1. Каждая координата суммывекторов равна сумме
соответствующих координат
a {2;3} + b {1;4} = c {3;7}
2. Каждая координата разности
векторов равна разности
соответствующих координат
a {2;3} - b {1;4} = c {1;-1}
18.
3. Каждая координатапроизведения вектора на
число равна произведению
соответствующей координаты
на это число
если a {2;5}, то -4 a {-8;-20}
19.
Задание: найти координатывектора p = 2 a – 1/3 b + c, если
a {1; -2}, b {0; 3}, c {-2; 3}
1) 2a {1*2; -2*2}, 2a {2; -4}
2) – 1/3b {0*(-1/3); 3*(-1/3)},
- 1/3 b {0; -1}
3) c {-2; 3}
4) p {2+0-2; -4-1+3}, p {0; -2}














 mathematics
mathematics








