1.1 лекция

1. Значение математики в профессиональной деятельности и повседневной деятельности

ЗНАЧЕНИЕ МАТЕМАТИКИ В
ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ И
ПОВСЕДНЕВНОЙ ДЕЯТЕЛЬНОСТИ

2. Цель:

ЦЕЛЬ:
Выяснить, каким образом используются знания, полученные
на занятиях математики в различных видах профессиональной
деятельности.
РЕЗУЛЬТАТЫ:
Понимание важности математических знаний в различных
профессиональных областях, таких как финансы, инженерия,
медицина и наука.
Освоение основных математических понятий, таких как
проценты, доли, вероятности и статистика, и их применение в
повседневной жизни, например, при планировании бюджета
или сравнении цен.
Развитие критического мышления и навыков решения задач,
что помогает в профессиональной деятельности и в личной
жизни.

3. 1. Предмет и задачи математики

1. ПРЕДМЕТ И ЗАДАЧИ
МАТЕМАТИКИ
•Математика (греч. maqhmatica – mathematike, от
maqhma – mathema – знание, учение, наука) – наука о
количественных отношениях и пространственных
формах действительного мира.
•Математика – самая древняя наука, игравшая
важнейшую роль в жизни и деятельности человека на
всех исторических этапах, т.к. людям всегда нужно
было чтолибо считать и чертить, измерять и
вычислять,
прогнозировать
и
проектировать,
создавать новое

4. математика

МАТЕМАТИКА
Математика (от др- греч. — изучение, наука) — наука о
структурах, порядке и отношениях, которая исторически
сложилась на основе операций подсчёта, измерения и
описания форм реальных объектов.
Математика
—
фундаментальная
наука,
предоставляющая (общие) языковые средства другим
наукам; тем самым она выявляет их структурную
взаимосвязь и способствует нахождению самых общих
законов природы.

5.

Математика играла и продолжает играть ключевую роль как в
профессиональной, так и в повседневной деятельности.
Древние ученые, такие как Пифагор, Евклид и Архимед,
сделали значительный вклад в развитие математики.
Пифагор, известный философ и математик, заявил: "Все есть
число". Эта фраза подчеркивает важность чисел и
математических отношений в понимании мира. Он основал
Пифагорейскую школу, которая изучала свойства чисел и их
значения в природе и музыке.

6.

Евклид, автор знаменитого труда "Начала", оказал огромное
влияние на развитие геометрии. В своей работе он
систематизировал математические знания своего времени и
установил основные аксиомы и теоремы.
Его слова "Математика - это наука о выводах, основанная на
очевидных истинах" подчеркивают важность логики и
доказательства в математике.

7.

Архимед, величайший математик и инженер, говорил: "Дайте
мне точку опоры, и я переверну Землю". Это утверждение
отражает не только его глубокое понимание физики и
механики, но и важность математических принципов в
решении практических задач. Архимед сделал многие
открытия в области геометрии, числа и механики, предлагая
методы вычисления площади и объема.

8.

В более поздние времена великие математики, такие как
Леонардо да Винчи, говорили: "Математика - это язык, с
помощью которого Бог написал мир". Это утверждение
подчеркивает, как математика помогает нам понимать и
описывать окружающий нас мир.

9.

Древнегреческий математик Аристотель также подчеркивал
важность математики, утверждая, что "математические науки
позволяют человеческому разуму достигать высшей истины".
Это говорит о том, что математика не только служит
практическим целям, но и способствует философскому и
научному осмыслению мира.

10.

Целью изучения математики является повышение общего
кругозора, культуры мышления, формирование научного
мировоззрения.
Чем больше человек познавал природу, создавал
механизмы, развивал науку, производство и торговлю, тем
весомее становился вклад математики. И это влияние было
взаимным – математика стала сложной и разветвленной.

11.

Сегодня можно говорить, что современная
математика – это “метанаука”, объединяющая
комплекс дисциплин: арифметику – теорию чисел,
алгебру, геометрию, математический анализ,
теорию
множеств,
теорию
вероятностей,
математическую статистику, теорию игр и многие,
многие другие (насчитывают несколько десятков
крупных
направлений).
На стыках наук
появляются разделы: математическая физика,
математическая
логика,
математическая
лингвистика, математическая экономика и др.

12.

Математика – необходимый инструмент познания в любой
отрасли человеческой деятельности – характеризуется
высокой степенью абстрактности ее понятий и высокой
степенью их обобщенности
По меткому выражению известнейшего ученого Нильса
Бора: “Математика – это больше, чем наука, это – язык”.
То есть язык, на котором можно ставить вопросы и
отвечать на них принципиально.

13.

Математика – это также и форма мышления.
Математика – наука, которая скорее тождественна
философии, чем остальным “содержательным наукам”; наука
инструментальная; наука, которая вступает в глубокие
органические связи с целым рядом других дисциплин
Математика — наука о структурах, порядке и отношениях,
которая исторически сложилась на основе операций
подсчёта, измерения и описания форм реальных объектов.

14.

Математика – наука, которая появилась для удобства
описания окружавших человека предметов их количества, их
свойств и форм.
Математика есть универсальный язык науки и мощный
метод научною исследования. История математики являет
собой грандиозное свидетельство интеллектуального
развития человечества за последние тысячелетия. Пьер
Гассенди утверждает: «В случае если мы что-то знаем, то это
благодаря изучению математики». По словам М. В.
Ломоносова, «Математику уже -затем учить нужно, что она
ум в порядок приводит»

15.

Для уяснения роли и значимости математики в научном
познании мира крайне важно понять, что такое
математика. Природа математики (как и любой науки)
определяется спецификой ее объекта и предмета
изучения, основными методами исследования, а также
выделением различных ее характерных черт.

16.

Объектом математики как науки являются фундаментальные
категории формы и количества, взятые в наиболее общем и
чистом виде, и всевозможные их проявления.
Предметом
математики
служат
разнообразные
математические структуры и математические модели,
которые появляются (открываются или изобретаются) в
результате интеллектуальной деятельности человека как
продукты рефлексии или отображение реальности. А общий
метод математики есть строгая дедукция.

17.

Задачи изучения математики:
-в результате освоения дисциплины обучающийся должен
уметь:
- решать прикладные задачи в области профессиональной
деятельности.
в результате освоения дисциплины обучающийся должен
знать:
- значение математики в профессиональной деятельности;
- основные математические методы решения прикладных
задач в области профессиональной деятельности;
- основные понятия и методы теории вероятностей и
математической статистики;
- основы интегрального и дифференциального исчисления.

18.

Математическое
образование
–
это
столетиями средство интеллектуального
условиях массового обучения:
испытанное
развития в
- воспитание
интеллектуальной
корректности,
критичности мышления;
- способность к абстрактному и логическому анализу.
Математическое
образование
способствует
формированию фундаментальных навыков, которые
необходимы не только для решения конкретных задач,
но и для успешной навигации в современном мире, где
аналитическое мышление играет ключевую роль.

19.

Итак, математика есть наука о форме и количестве
и четких схемах их бытия и воплощения. По этой
причине математика универсальна как метод,
аппарат исследования и получения научного знания и
как точный язык его описания. Математика имеет
многочисленные теоретические и практические
приложения, адекватные действительности. Именно
в рамках математики возник общенаучный
дедуктивный метод, широко применяемый не только
в естествознании и технике, но и в гуманитарных
науках и обществоведении.

20.

В случае если естественные науки изучают природу, а
гуманитарные и социальные науки - человека и
человеческое общество, то математика исследует в
ее же недрах полученные абстракции, то есть в
известном смысле самое себя. В этом отношении
математика
близка
к
философии,
научная
составляющая которой отражена в постоянно
развивающейся системе философских категорий.

21.

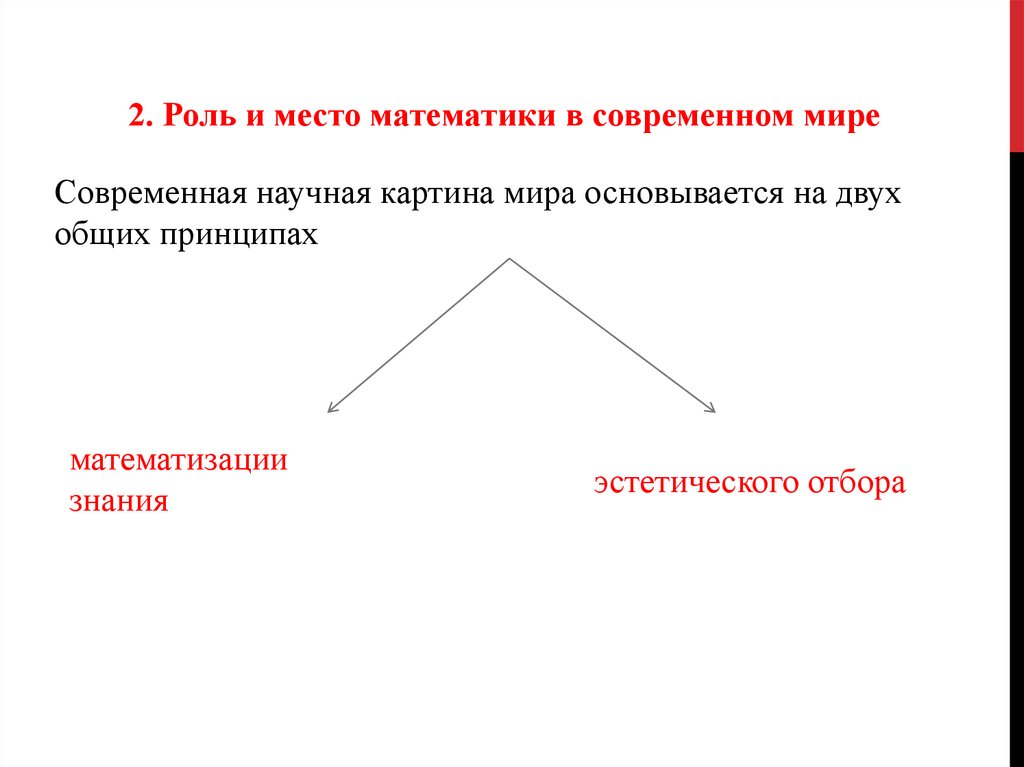
2. Роль и место математики в современном мире
Современная научная картина мира основывается на двух
общих принципах
принцип
математизации
знания
принцип
гармонии
(эстетического отбора

22.

МАТЕМАТИЗАЦИЯ ЗНАНИЙ ПРЕДПОЛАГАЕТ
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ И
МОДЕЛЕЙ ДЛЯ ОПИСАНИЯ, АНАЛИЗА И
ПРЕДСКАЗАНИЯ ЯВЛЕНИЙ В РАЗНЫХ ОБЛАСТЯХ
НАУКИ.
ЭСТЕТИЧЕСКИЙ ОТБОР, С ДРУГОЙ СТОРОНЫ,
СВЯЗАН С ТЕМ, КАК ТЕОРИЯ ИЛИ МОДЕЛЬ
ВОСПРИНИМАЕТСЯ И ПРИНИМАЕТСЯ НАУЧНЫМ
СООБЩЕСТВОМ. НАУЧНЫЕ ТЕОРИИ ДОЛЖНЫ НЕ
ТОЛЬКО ОБЪЯСНЯТЬ НАБЛЮДАЕМЫЕ ЯВЛЕНИЯ, НО
И ИМЕТЬ ОПРЕДЕЛЕННУЮ ЭСТЕТИЧЕСКУЮ
ПРИВЛЕКАТЕЛЬНОСТЬ — БЫТЬ ПРОСТЫМИ,
ЭЛЕГАНТНЫМИ И ГАРМОНИЧНЫМИ.

23.

Принцип математизации заключается, во-первых, в
широком применении математических методов и
теорий в других науках, технике и практике и, вовторых, в построении наук, особенно естественных,
по образу и подобию математики, дедуктивно.

24.

Математика занимает особое место среди других наук.
Математику нельзя причислять к естествознанию (т.к.
исключает наблюдение и эксперимент), хотя и
зародилась она из практики как естественная наука.
Математика развивалась, углубляясь в абстракцию и
формализованное мышление. Она стала не только
инструментом для решения практических задач, как,
например, в архитектуре, инженерии или экономике,
но и самостоятельной наукой, исследующей
структуры, взаимоотношения и закономерности.

25.

Приложения математики весьма разнообразны.
Принципиально область применения
математических методов не ограничена: все виды
движения материи могут изучаться математически.
Однако роль и значение математических методов в
различных случаях не одинаковы. Никакая
математическая схема не исчерпывает всей
конкретности действительных процессов.

26.

Типичным
примером
полного
господства
математических методов можно считать небесную
механику, в частности, учение о движении планет.
Имеющий очень простое математическое выражение
закон всемирного тяготения почти полностью
определяет изучаемый здесь круг явлений. При
переходе от механики к физике несколько
возрастают трудности применения математического
аппарата (выбор предпосылок использования
математики и трактовка результатов).

27.

В других естественных науках (например, биологических)
математические методы играют более подчиненную роль. В
еще большей степени математика предоставляет свои
возможности непосредственному анализу явлений и
процессов во всей их конкретной сложности в социальных и
гуманитарных науках (часто математика остается лишь в
форме подсобной науки – математической статистики).
В окончательном же анализе социальных (и правовых)
явлений и процессов математика вообще уходит на задний
план, полностью уступая свое место качественному
своеобразию
каждого
временного
(исторического)
промежутка.

28.

Причина, по которой без математических методов сейчас не обходится не
только техника, механика, электроника, экономика, но и медицина,
экология, психология, социология, лингвистика, история, юриспруденция
и др., проста – для математических методов характерны:
Структурированность: математические методы основаны на
четких и логически организованных правилах и принципах.
Формализованность: использование символов и обозначений
для описания математических понятий и отношений.
Абстрактность: применение общих понятий и моделей для
решения конкретных задач, позволяющее выделять важные
элементы из общего контекста.
Доказательность: все утверждения и теоремы обосновываются
строгими математическими доводами и доказательствами.
Универсальность: математические методы применимы в
различных областях знаний, включая естественные науки,
социальные науки и инженерные дисциплины.

29.

Использование математических методов формирует так называемый
математический стиль мышления, т.е. абстрактный, логический,
идеально строгий и – самое главное – нацеленный на поиск
закономерностей.
Профессионал,
грамотно
и
аккуратно
применяющий математические методы, способен принести пользу в
любой сфере деятельности, в том числе и медицине.

30.

Математика - необходимый атрибут любой науки
Основные причины:
• органическое единство природы и общества;
• содержательный понятийный аппарат (например,
доказательство,
множество,
функция,
модель,
операция);
• правовые системы, явления и процессы наряду с
качественными свойствами обладают и количественной
мерой;
• в некоторых областях права (криминалистика,
криминология, государственное управление и др.)
просто не обойтись без количественных параметров.

31.

В математике используют два вида умозаключений:
Индукция и дедукция.
Индукция подразумевает обобщение на основе
конкретных примеров и наблюдений, позволяя
формировать обобщенные выводы или теории.
Дедукция, с другой стороны, основана на применении
общих принципов или аксиом для вывода конкретных
следствий. Оба типа умозаключений играют важную
роль в математическом мышлении и исследовании.

32.

Математика
играет
важную
роль
в
естественнонаучных, инженерно-технических и
гуманитарных
исследованиях.
Причина
проникновения математики в различные отрасли
знаний заключается в том, что она предлагает
весьма четкие модели для изучения окружающей
действительности в отличие от менее общих и более
расплывчатых моделей, предлагаемых другими
науками

33.

Математика применяется
практически во всех областях
человеческой деятельности, в
разных профессиях. Убедимся в
этом на примерах.

34. Математика в кулинарии

МАТЕМАТИКА В
КУЛИНАРИИ Математика в кулинарии имеет
большое значение, так как для
приготовления
любого
блюда
должен соблюдаться рецепт. В
рецепте
указывается
точное
соотношение продуктов, которое
необходимо соблюдать в процессе
приготовления. При взвешивании
продуктов
в
кулинарии
используются
математические
величины масса и объём. Ими тоже
необходимо уметь пользоваться.
Единицы времени играют далеко
не
последнюю
роль
в
приготовлении
блюд.
Приготовленные
блюда
нужно
умело делить на порции, в чём нам
опять же поможет математика.

35. Математика в торговле

МАТЕМАТИКА В
ТОРГОВЛЕ
Математика в торговле имеет
важнее всего. Работники торговли
должны хорошо знать числа,
уметь их складывать и вычитать,
умножать и делить. Без этого
продавцы не смогли бы сосчитать
товар в магазине. Не могли бы
вести
ведомости
расхода
и
прихода прибыли в магазине. С
помощью
математических
вычислений продавцы считают
стоимость
приобретённого
покупателем товара, отсчитывают
сдачу.

36. Математика в раскрое одежды

МАТЕМАТИКА В
РАСКРОЕ ОДЕЖДЫ
Прежде чем сшить одежду,
необходимо снять все мерки с
человека, и тут не обойтись без
математики.
Сантиметровой
лентой нужно сделать замеры
(длину рукавов, ширину, длину
костюма или платья и другое),
записывая их в тетрадь. Потом по
журналу мод нужно выбрать фасон
одежды и по ранее замеренным
цифрам мерки рассчитать и
начертить выкройку. При помощи
математических расчётов оставим
запас ткани на припуск и подгиб,
только после этого делаем раскрой
ткани для шитья из него одежды.
Как говорится, семь раз отмерь,
один раз отрежь.

37. Математика в строительстве

МАТЕМАТИКА В СТРОИТЕЛЬСТВЕ
В строительстве без математики
никак не обойтись. Посудите сами:
Надо уметь измерять высоту,
ширину, длину предметов? Надо.
Надо уметь вычислять размеры
дверей, окон, комнат, квартир?
Надо. Как подсчитать количество
нужного строительного материала,
если не знаешь математику?
Никак! Математику применяли
ещё задолго до нашей эры. В
Древнем Вавилоне при помощи
математических расчётов строили
водопроводы и подавали в дома
воду. В Древнем Египте по
математическим расчётам строили
пирамиды.

38.

Применение математики в землеустройстве
В настоящее время в землеустроительной проектной организации,
стационарные службы и частные землемеры оснащены современной
техникой. Землеустроительные организации нуждаются в
инженерных кадрах, хорошо владеющими математическими
методами обработки кадастровой информации. Возможно,
математический метод в землеустройстве обусловлен тем, что
основные
решения
проектов
землеустройства
имеют
многовариантный характер, а искомые величины, как правило,
выражают численно, их можно связать с системой уравнения
неравенства и объединить с целевой установкой.

39.

Для решения землеустроительных задач
различных
классов,
используют
разнообразные виды экономических,
математических моделей, позволяющих
проводить
анализ
использования
земельных
ресурсов,
выявить
определенные тенденции и находить
оптимальные
варианты
устройства
территории.

40.

Графические математические модели дают характеристику различным
элементам проекта землеустройства или их совокупности, которые
показываются на проектном плане, к ним относится площадь,
линейные и точечные объекты.
Линейные объекты - это линейные объекты организации территории,
полевые и магистральные дороги, лесополосы, инженерные
коммуникации (газопровод, ЛЭП), отдельные границы участков, зон и
т.д. Эти объекты могут размещаться в виде прямых и ломаных линий,
а также кривых. Они характеризуются протяженностью, а также
шириной, координатами начальных, конечных и промежуточных
точек.
Точечные объекты - позволяют определить на местности
местоположение отдельных инженерных сооружений (колодцы,
родники, буровые вышки и т.д.) их размещение, характеристики
местоположения.

41. Математика в профессии сварщика

МАТЕМАТИКА В ПРОФЕССИИ СВАРЩИКА

42. Зачем математика сварщику?

ЗАЧЕМ МАТЕМАТИКА СВАРЩИКУ?
Сварщик — рабочая специальность, предусматривающая
работу на сварочном производстве.
Создание сварной
конструкции, полностью отвечающей своему служебному
назначению, надежной в эксплуатации, представляет собой
комплексную задачу, которая включает проектирование,
расчет, рациональное построение технологии изготовления. Все
это требует определенных математических знаний –
вычислительных навыков, знания правила пропорции, умения
нахождения неизвестного и др., и, конечно же, немало знаний
из области геометрии. Геометрическое проектирование
сварочной конструкции помогает не только уменьшить время,
затрачиваемое на создание изделия, но и позволяет свести до
минимума изменения, вносимые в конструкцию, практически
исключить ошибки и улучшить качество изделия.

43. Математика в профессии бухгалтера

МАТЕМАТИКА В ПРОФЕССИИ БУХГАЛТЕРА

44. Зачем Бухгалтеру Математика?

ЗАЧЕМ БУХГАЛТЕРУ МАТЕМАТИКА?
Бухгалтер — специалист, в обязанности которого
входит документальное ведение финансово-хозяйственного
учета предприятия.
Работа
бухгалтера
строго
регламентирована
действующим
законодательством
и
стандартами
бухгалтерского учета, в том числе международными.
Именно у математики бухгалтерия позаимствовала
свою основную отличительную черту – точность. От
использования простых действий арифметического счёта с
течением времени она стала использовать методы
дифференциального и интегрального исчисления, теорию
множеств.

45. Математика в профессии плотника

МАТЕМАТИКА
В ПРОФЕССИИ ПЛОТНИКА

46. Зачем плотнику математика?

ЗАЧЕМ ПЛОТНИКУ МАТЕМАТИКА?
Плотник - выполняет работы, связанные с
обработкой древесины и изготовлением из нее
разнообразных деталей, изделий и строительных
конструкций.
Так как многие плотницкие сооружения и
конструкции должны обеспечивать безопасность
людей, пользующихся ими в своей
профессиональной деятельности (леса, висячие
стропила, балки и пр.), плотник должен обладать
высоким чувством ответственности, точностью и тут
не обходимы знания математики.

47. Математика в профессии фотографа

МАТЕМАТИКА
В ПРОФЕССИИ ФОТОГРАФА

48. Зачем нужна математика фотографу?

ЗАЧЕМ НУЖНА МАТЕМАТИКА
ФОТОГРАФУ?
Выбрать точку расположения объекта съёмки помогает
знание золотого сечения. Напомним, что золотым
сечением называют такое деление целого на части, когда
отношение большей части к целому равно отношению
меньшей части к большей. Значение этого отношения,
приближённо равное 5/8, называют числом Фидия.

49.

На практике не так-то легко на глаз построить золотое
сечение. Поэтому при съёмке можно использовать несколько
упрощённый композиционный приём — так называемое
правило третей, когда стороны кадра делятся не по золотому
сечению, а просто на три равные части.

50.

С точки зрения математики
обычный фотоснимок — это
изображение на плоскости,
полученное
путём
проектирования его из одной
точки. Однако мы хотим
отобразить
реальность
с
максимальной достоверностью
и поэтому ищем новые средства
для
демонстрации
трёхмерности пространства и
окружающих нас предметов.
Одно из таких средств —
линейная
перспектива.

51. Математика в профессии программиста

МАТЕМАТИКА В ПРОФЕССИИ
ПРОГРАММИСТА

52. Зачем программисту математика?

ЗАЧЕМ ПРОГРАММИСТУ
МАТЕМАТИКА?
Изучение математики формирует своеобразный
метод мышления, который позволяет очень
эффективно решать задачи (не писать программы, а
именно решать задачи), а также позволяет видеть
многие ошибки в предложенных решениях.
Будущему программисту важно научиться думать,
находить верные решения, «шевелить мозгами».

53.

Вопросы для самоконтроля:
Расскажите о роли математики в науке, технике, экономике,
информационных технологиях и практической деятельности.
Сформулируйте
обучающимисяпри
цели и
задачи, стоящие перед
изучении дисциплины «Математика».
Приведите примеры использования математических понятий
в Вашей специальности.

54.

Темы для докладов, которые студенты могут написать на тему
базовых знаний и умений по математике в профессиональной и
повседневной деятельности (на практическое занятие):
1. Роль арифметики в повседневной жизни : анализ ситуаций, где
необходимы базовые вычисления.
2. Математические модели в экономике : как цифры помогают
принимать финансовые решения.
3. Статистика и ее применение в маркетинге : как анализ данных
помогает компаниям понимать потребительские предпочтения.
4. Геометрия в архитектуре : использование математических
принципов для проектирования зданий и структур.
5. Применение процентов в финансовом планировании : как
управлять личным бюджетом с учетом процентов по кредитам и
депозитам.
6. Теория вероятностей в повседневных решениях : как количество
возможных вариантов влияет на риск и выбор.
7. Место математики в науке : как математические расчетки
помогают в научных исследованиях.

55.

Спасибо за внимание!