3сем_Лк 6_ЛОДУ с пост коэф.Метод Лагранжа (2)

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Кафедра высшей математики
Лекция 6.
Линейные однородные и неоднородные ДУ
с постоянными коэффициентами
22.12.2025
г. Санкт-Петербург
2025
1|11

2.

Линейное неоднородное ДУ 2-го порядка с
постоянными коэффициентами
y p y q у f (x) (1
ЛНДУ
)
f (x) правая часть
f ( x) 0 ЛОДУ y + p y + q y 0
(2)
f(x) непрерывна для х (a,b) ЛНДУ имеет единственное решение
Л. Эйлер – способ построения ФСР ЛОДУ
kx
(2)
k = const (неизвестна)
y e ,
y ke , y k e
kx
2 kx
e
kx
(k pk q) 0
2
дискриминант
D p 4q
2
2|11
k pk q 0
2
характеристическое ур–е

3.

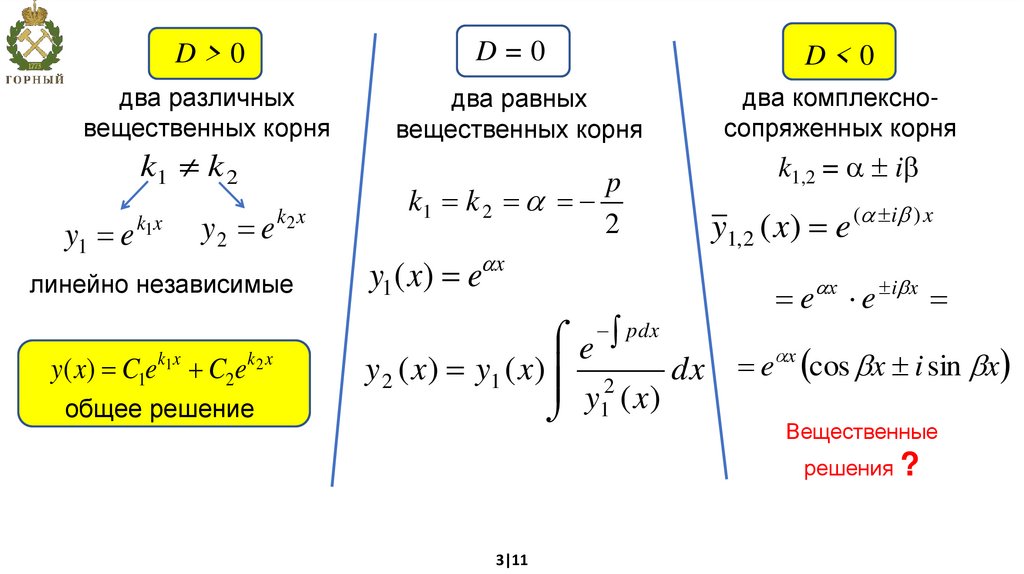
D>0
D=0
D<0
два различных
вещественных корня
два равных
вещественных корня
два комплексносопряженных корня
k1 k 2
y1 e
k1x
y2 e
k2 x
линейно независимые
y( x) C1ek1x C2ek 2 x
общее решение
p
k1 k 2
2
x
y1 ( x) e
pdx
k1,2 = i
y1, 2 ( x) e
e
х
( i ) x
e
i x
e
x
y 2 ( x) y1 ( x) 2
dx e cos x i sin x
y ( x)
1
Вещественные
решения ?
3|11

4.

два равных
вещественных корня
2
p
y1 ( x)
2
e pdx
y 2 ( x) y1 ( x) 2
dx
y1 ( x)
e
x
dx
e
pdx
р dx
e
e
px
px
x e
px
e px dx
e
y2 ( x ) xe x
Определитель
Вронского :
x
y1 ( x) e
y2 ( x ) xe
e
2
p
x
e 2
x
линейно независимые
w( x)
e
x
x
xe
e x e x 1 x
e 2 x 1 x хe 2 x e 2 x 0
общее решение: y( x) C1e x C 2 xe x C1 C 2 x e x
4|11

5.

два комплексно-сопряженных корня
линейная комбинация:
y1 ( x) e x cos x i sin x
y2 ( x) e x cos x i sin x
y1 y 2
x
y1 ( x)
e cos x
2
y1 y 2
x
y 2 ( x)
e sin x
2i
линейно
независимые
решения
общее решение:
y( x) C1e
x
x
x
cos x C 2 e sin x e (C1 cos x C 2 sin x)
5|11

6.

Пример 2. Решить ДУ у 6 у 9 у 0.
Пример 1. Решить ДУ у 4 у 3 у 0.
Характеристическое ур–е: k
D =4
y1 e
k1 1
4k 3 0
2
Характеристическое ур–е:
x
(k 3) 2 0
ФСР
3
x
k2 3
y2 e
общее решение: y C1e
Пример 3. Решить ДУ
x
C2 e
k 6k 9 0
2
k1 k 2 3
Ф С Р:
y1 e
3x
3x
y 2 xe
3x
общее решение:
y e 3 x (C1 C 2 х)
у 4 у 5 у 0.
Характеристическое ур– k 4k 5 0 (k 2)
е:
k 1 2 i
2
два комплексно
1
сопряженных корня: k 2 2 i
2
общее решение: у e
6|11
2 x
2
1
D = –1
y1 e 2 x cos x
Ф С Р : y e 2 x sin x.
2
(C1 cos x C 2 sin x)

7.

:
y p y q у f (x) (1
ЛНДУ
)
Теорема о структуре общего
решения.
y
Общее решение у(х) ЛНДУ (1) – сумма любого частного решения (x)
этого уравнения и общего решения y (x) соответствующего ЛОДУ (2):
y ( x) y ( x) y ( x)
y ( x) C1 y1 ( x) C 2 y 2 ( x)
у1(х), у2(х) – ФСР ЛОДУ(2)
y ( x) y ( x) C1 y1 ( x) C2 y2 ( x).
частное реш.
ЛНДУ
6|11
общее реш.
ЛОДУ

8.

Метод вариации произвольных постоянных (метод Лагранжа)
Идея метода: искать общее решение ЛНДУ (1) в том же виде, как и для
ЛОДУ (2), где произвольные постоянные С1(х) и С2(х) – функции от х :
y ( x) C1 ( x) y1 ( x) C2 ( x) y2 ( x)
С1(х) и С2(х) – непрерывно-дифференцируемы
в интервале (a,b)
система
функциональных
уравнений
C1 ( x) y1 C 2 ( x) y 2 0;
C1 ( x) y1 C 2 ( x) y 2 f ( x).
находим
после интегрирования
неизвестные: C1 ( x) C2 ( x) получим функции С (х) и С (х)
1
8|11
2
общее
решение
ЛНДУ

9.

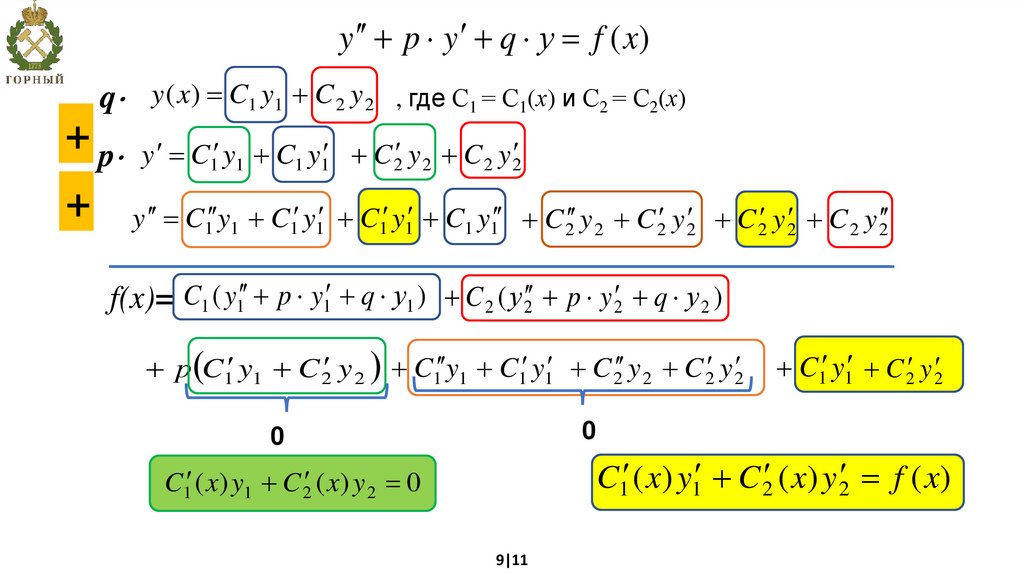
y p y q у f (x)
q y ( x) C1 y1 C 2 y 2 , где С1 = С1(х) и С2 = С2(х)
+ p y C1 y1 C1 y1 C 2 y 2 C 2 y 2
+
y C1 y1 C1 y1 C1 y1 C1 y1 C 2 y 2 C 2 y 2 C 2 y 2 C 2 y 2
f(x)= C1 ( y1 p y1 q у1 ) C 2 ( у 2 p y 2 q у 2 )
p C1 y1 C 2 y 2 C1 y1 C1 y1 C 2 y 2 C 2 y 2
C1 y1 C 2 y 2
0
0
C1 ( x) y1 C 2 ( x) y 2 f ( x)
C1 ( x) y1 C 2 ( x) y 2 0
9|11

10.

Пример 5. Решить ДУ y y 2x.
y y 0.
ЛОДУ:
характеристическое
уравнение:
k 1 0
2
y1 e
x
y2 e
k1 1
k 2 1
общее решение:
y C1e C 2 e
x
x
Общее решение ЛНДУ
ищем в виде:
x
y C1 ( x)e C 2 ( x)e .
x
x
Найдем функции С1(х), С2(х) :
x
C1 ( x)e C2 ( x)e 0 ;
x
x
C1 ( x)e C2 ( x)e 2 x,
x
C1 ( x) xe
C1 ( x) xe x dx ( x 1)e x C1
x
C 2 ( x) xe
x
y( x) 2 x C1e C 2 e
x
частное
реш. ЛНДУ
x
общее реш. ЛОДУ
10|11
C 2 ( x) xe x dx (1 x)e x C 2

11.

Спасибо за внимание
Кафедра высшей математики;
Санкт-Петербургский горный
университет императрицы
Екатерины II;
199106, Санкт-Петербург,
Васильевский остров, 21 линия д.2;
Тел.: +7(812) 328-82-31;
E-mail: kafmatem@spmi.ru
11|11