3сем_Лк 1_ДУ (2)

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1-ГО ПОРЯДКА.
ДУ С РАЗДЕЛЕННЫМИ И РАЗДЕЛЯЮЩИМИСЯ
ПЕРЕМЕННЫМИ
21.12.2025
ДОРОФЕЕВ А.В., д.п.н., профессор кафедры высшей математики
г. Санкт-Петербург
2024
1|14

2.

Содержание лекции
• Понятие дифференциального уравнения (ДУ);
• Порядок ДУ;
• Общее и частное решения ДУ;
• Интегральная кривая;
• Задача Коши;
• Теорема о существовании и единственности решения задачи
Коши;
• ДУ с разделенными и разделяющимися переменными.
2|14

3.

Обыкновенное ДУ –
уравнение, содержащее независимую переменную х,
(n)
неизвестную функцию у(х) и ее производные y ( x ), y ( x ), , y ( x )
(или дифференциалы dx, dy, …, dxn, d ny).
Порядок ДУ – это порядок старшей производной в уравнении
(или дифференциала).
ДУ в неявной форме:
F(x, y(x), y′(x),…, y(n)(x)) = 0
ДУ в явной форме: y(n)(x) = f (x, y(x), y′(x),…, y(n-1)(x))
3|14

4.

Примеры обыкновенных ДУ
ДУ 1-го порядка
ДУ 2-го порядка
xy ( x) 2 y ( x) y ( x) 0, x 1 y dx y 1 x dy 0
3
2
2
y ( x) 5 y ( x) xe 0
x
3
2x
y ( x )
ДУ 3-го порядка
y ( x )
Решение ДУ n- го порядка в интервале (а, b) – функция у = (х),
которая n раз дифференцируема и обращает исходное уравнение в
тождество.
График решения ДУ называют интегральной кривой уравнения.
Процесс отыскания решений ДУ – интегрирование уравнения.
Если решение получено в неявной форме Ф(х,у)=0, то такое выражение называют общим интегралом ДУ
4|14

5.

Простейшее обыкновенное ДУ 1-го порядка
y ( x) f ( x)
или
Пример 1. Решить ДУ:y ( x) x
2
dy
f (x)
dx
3
Непосредственное интегрирование:
Функция
3
x
y ( x) x dx
C
3
2
x
y ( x)
C – решение ДУ, т.к. обращает уравнение в тождество.
3
Общий вид ДУ 1- го порядка:
F ( x, y ( х), y ' ( х)) 0 ,
где x - независимая переменная,
y - неизвестная функция,
F- заданная функция трех переменных.
5|14
(1)

6.

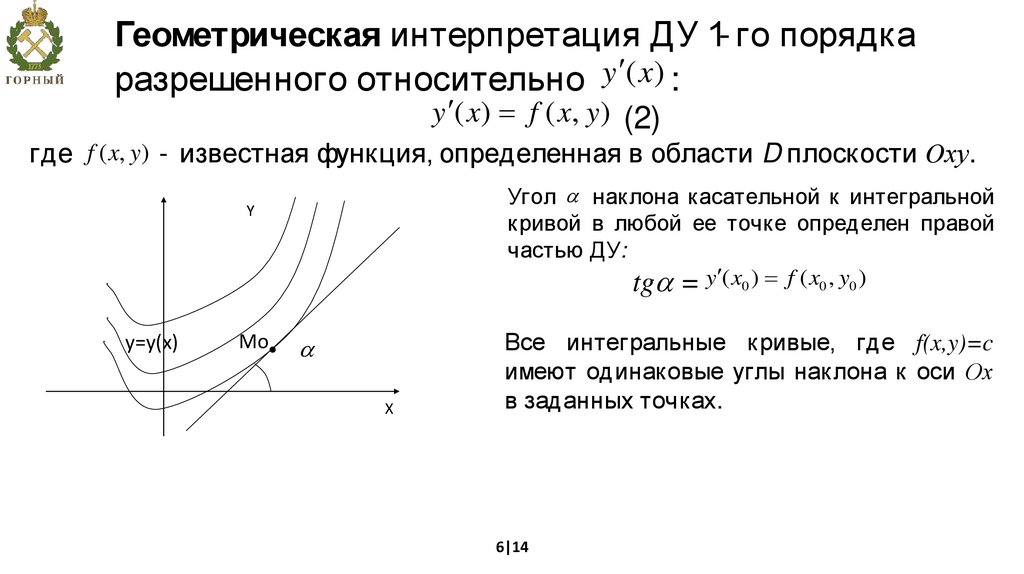
Геометрическая интерпретация ДУ 1- го порядка
разрешенного относительно y (x) :
y ( x) f ( x, y ) (2)
где f ( x, y) - известная функция, определенная в области D плоскости Oху.
Угол наклона касательной к интегральной
кривой в любой ее точке определен правой
частью ДУ:
tg = y ( x0 ) f ( x0 , y0 )
Y
y=y(x)
Mo
X
Все интегральные кривые, где f(x,y)=c
имеют одинаковые углы наклона к оси Ох
в заданных точках.
6|14

7.

Общее решение ДУ 1-го порядка (1) или (2)
это функция у =
(х, С), зависящая от одной произвольной
постоянной С, которая удовлетворяет условиям:
1)является решением ДУ при любом значении постоянной С;
2) при любом начальном условии у(х0)=y0 , можно найти такое
значение С=С0, что функция у = (х, С0) удовлетворяет данному
начальному условию.
Задача Коши для ДУ 1-го порядка:
найти решение ДУ (1) или (2),
удовлетворяющее начальному условию у(х0)=y0.
7|14

8.

Пример 2. Найти решение ДУ:y ( x) 2 x
1
для начального условия у(1) = 3.
2 x
Интегрируя уравнение, находим общее решение:
1 1 / 2
y ( x) 2 xdx x dx x 2 x C
2
Из начального условия определим неизвестную постоянную С: 1+1 + С = 3
Решение задачи Коши: y ( x) x 2 x 1
Теорема Коши (о существовании и единственности решения ДУ 1-го порядка).