Интегралы в музыке

1. «Интегралы в музыке.»

Карманов Руслан, Ухова Ксения 13КД

2. Введение

Интегралы - математический инструмент для работы с непрерывными
функциями.
В музыке применяются для анализа, обработки и создания звуковых
сигналов, которые меняются во времени.

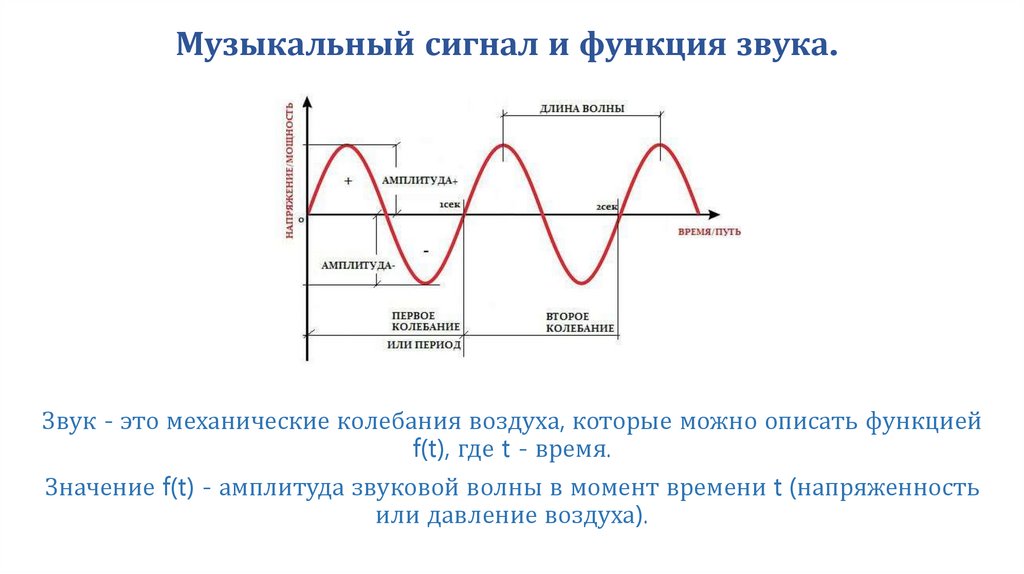
3. Музыкальный сигнал и функция звука.

Звук - это механические колебания воздуха, которые можно описать функцией
f(t), где t - время.
Значение f(t) - амплитуда звуковой волны в момент времени t (напряженность
или давление воздуха).

4. Интеграл для измерения энергии (мощности) звука.

Звуковая энергия пропорциональна интегралу от квадрата функции
амплитуды:
Энергия = ∫ f(t)² dt на интервале времени.
Это объясняется тем, что мощность сигнала зависит от квадрата амплитуды
(аналогично физике волн).

5. Пример с синусоидальным тоном:

Пусть f(t) = sin(2πft) это чистая звуковая волна с частотой f, тогда
интеграл энергии за полный период t = 1/f:
энергия = ∫₀ᵀ sin²(2πft) dt = t/2.
Это означает, что средняя мощность сигнала — половина максимума
амплитуды.

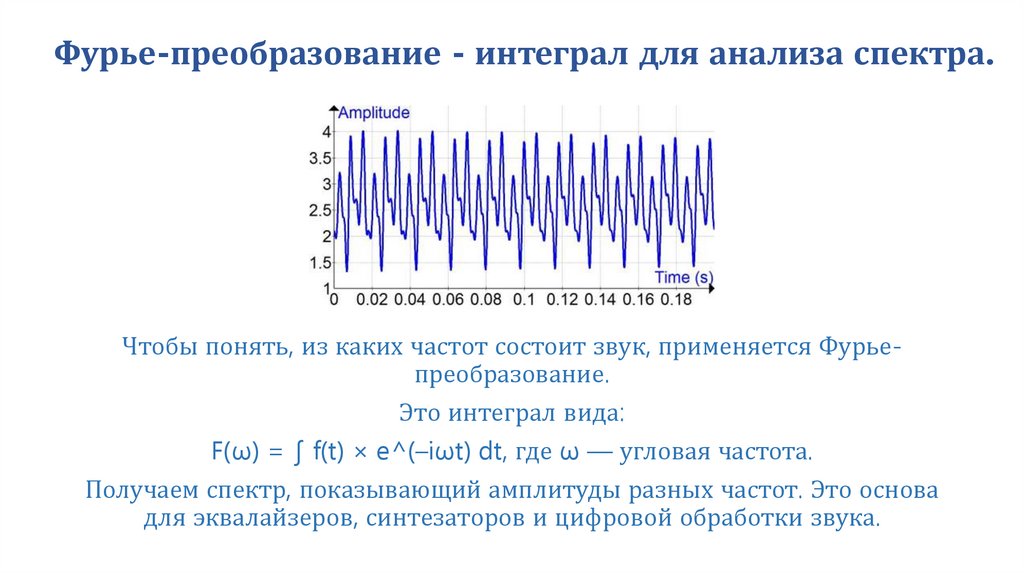
6. Фурье-преобразование - интеграл для анализа спектра.

Чтобы понять, из каких частот состоит звук, применяется Фурьепреобразование.
Это интеграл вида:
F(ω) = ∫ f(t) × e^(–iωt) dt, где ω — угловая частота.
Получаем спектр, показывающий амплитуды разных частот. Это основа
для эквалайзеров, синтезаторов и цифровой обработки звука.

7. Усреднение громкости через интеграл.

Громкость часто измеряется как среднее значение амплитуды или её
квадрата за время:
Уровень громкости = sqrt( (1/(b–a)) × ∫ₐᵇ f(t)² dt )
Это позволяет услышать, насколько громким воспринимается звук, и
регулировать его.

8. Применение в музыке и звуковой инженерии.

Создание реверберации - интегралы позволяют моделировать затухание и
отражения звука во времени.
Фильтрация и сведение треков - интегральные методы помогают сглаживать и
смешивать сигналы без резких изменений.
Анализ звуков для распознавания и синтеза речи и музыкальных
инструментов.

9. Вывод

Интегралы помогают преобразовать временные звуковые сигналы в
удобные для анализа и обработки формы, особенно в частотной
области.
Интегралы это фундамент в цифровой обработке звука, звукоинженерии
и музыкальном программировании.