Санау жүйелері

1.

Санау жүйелері
Оқытушы:
Аккасынова Жамиля
тел.: 8(702)624-77-79
e-mail: zhami_2990@mail.ru

2.

Сан қандай да бір алфавит символымен немесе символдар
тізбегімен өрнектеледі. Мұндай символдарды цифр деп атайды.
Санау жүйелері – бұл сандарды өрнектеудің қандай да бір тәсілі
және оған сәйкес сандармен әрекет жасау ережелері.
Сан
Информатика
Матема
-тика

3.

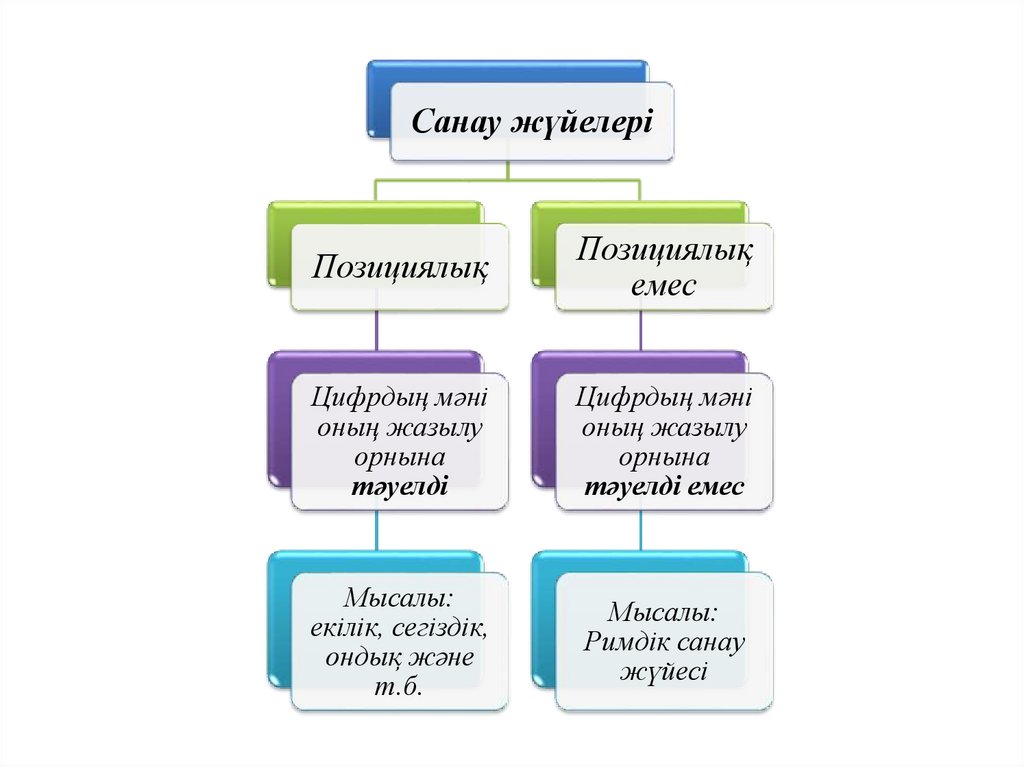
Санау жүйелері
Позициялық
Позициялық
емес
Цифрдың мәні
оның жазылу
орнына
тәуелді
Цифрдың мәні
оның жазылу
орнына
тәуелді емес
Мысалы:
екілік, сегіздік,
ондық және
т.б.
Мысалы:
Римдік санау
жүйесі

4.

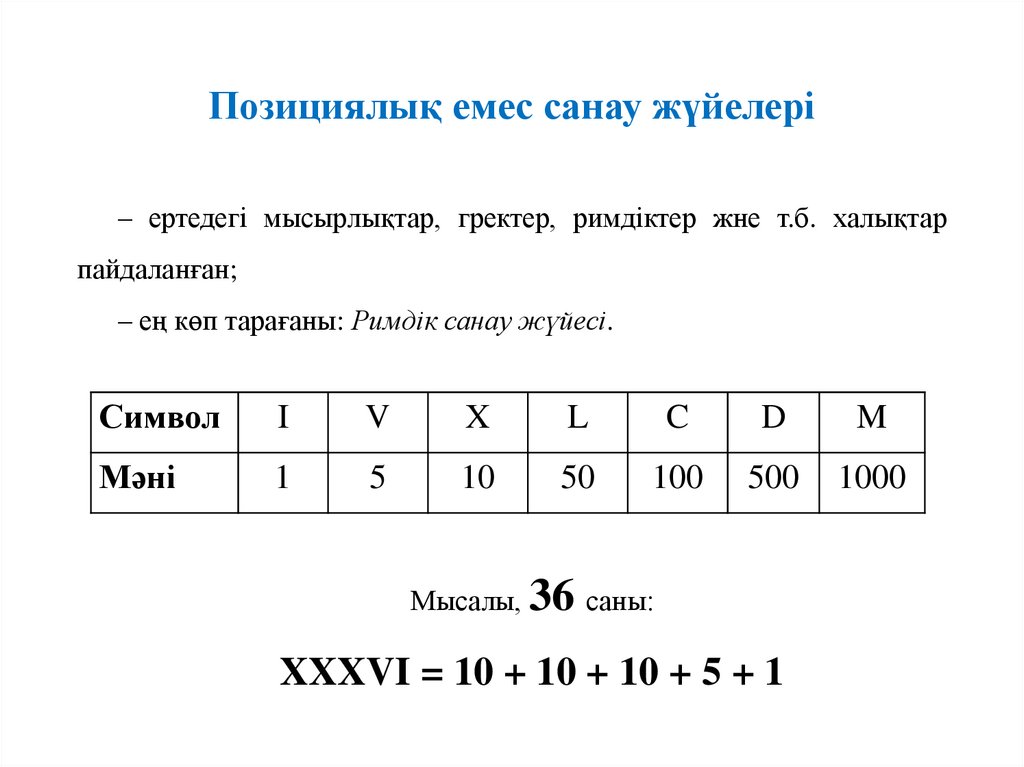
Позициялық емес санау жүйелері
– ертедегі мысырлықтар, гректер, римдіктер жне т.б. халықтар
пайдаланған;
– ең көп тарағаны: Римдік санау жүйесі.
Символ
I
V
X
L
C
D
M
Мәні
1
5
10
50
100
500
1000
Мысалы, 36 саны:
XXXVI = 10 + 10 + 10 + 5 + 1

5.

Позициялық емес санау жүйелері
Кемшіліктері:
үлкен сандарды жазу үшін үнемі жаңа таңбаларды енгізіп отыру
қажет;
бөлшек және теріс таңбалы сандарды өрнектеу мүмкін емес;
арифметикалық амалдарды орындау қиын.
Разряд (позиция, орын) – позициялық сандар жүйесіндегі сандарды
ұсынудың құрылымдық элементі.

6.

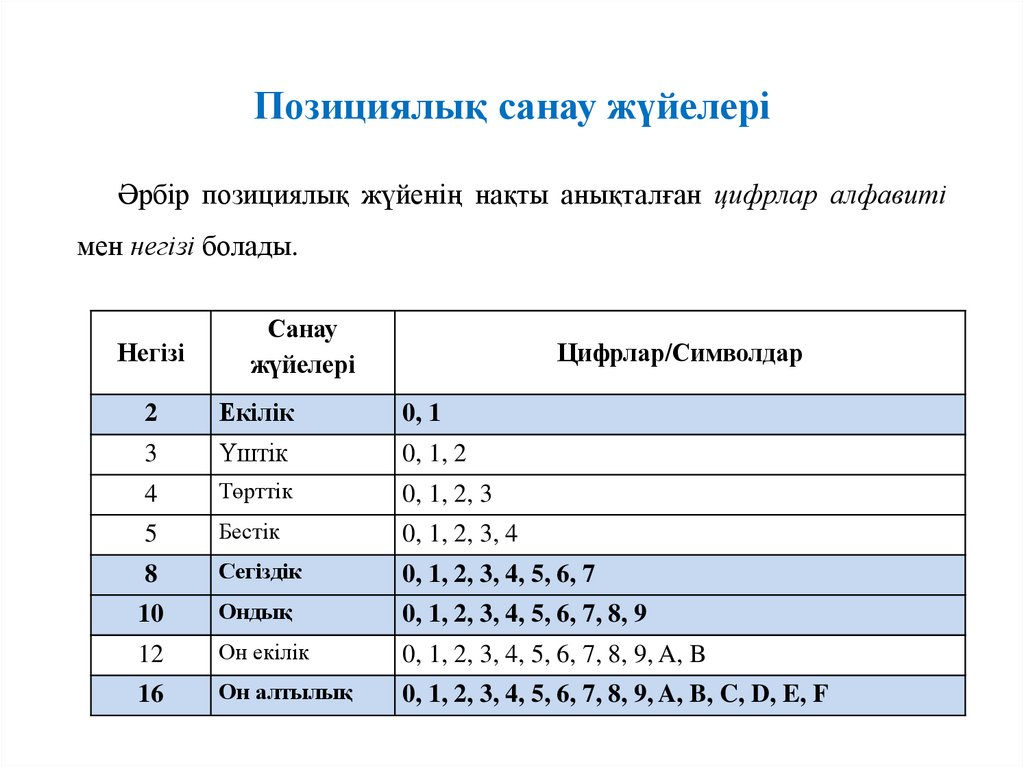
Позициялық санау жүйелері
Әрбір позициялық жүйенің нақты анықталған цифрлар алфавиті
мен негізі болады.
Негізі
Санау
жүйелері
Цифрлар/Символдар
2
Екілік
0, 1
3
Үштік
0, 1, 2
4
Төрттік
0, 1, 2, 3
5
Бестік
0, 1, 2, 3, 4
8
Сегіздік
0, 1, 2, 3, 4, 5, 6, 7
10
Ондық
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
12
Он екілік
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
16
Он алтылық
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

7.

Ондық санау жүйесі
он бірегей (қайталанбайтын)
цифрлардан (0, 1, 2, 3, 4, 5, 6, 7, 8, және 9) тұрады.
Сондықтан да негізі 10 санау жүйесі деп те аталады. Адамдар
ондық санау жүйесін күнделікті өмірде санау үшін қолданады.

8.

Екілік санау жүйесі 0 мен 1-ден тұрады. Сондықтан да
негізі 2 санау жүйесі деп те аталады.
Екілік жүйеде кез келген сан 0 мен 1 цифрларының көмегімен
жазылады да, екілік сан деп аталады.
Екілік санның әрбір разрядын (цифрын) бит деп атайды.
Мысалы:

9.

Екілік санау жүйесі
Артықшылығы:
– цифрды ұсыну ыңғайлылығы және компьютер құрылғысының
қарапайымдылығы;
Кемшілігі:
– санды жазу үшін 0 мен 1 цифрлары көп қажет;
– адамның қабылдауын қиындатады;

10.

Сегіздік санау жүйесі сегіз бірегей цифрлардан (0, 1, 2, 3,
4, 5, 6, 7) тұрады. Негізі 8 санау жүйесі деп те аталады.
Сегіздік
0
1
2
3
4
5
6
7
Екілік
000
001
010
011
100
101
110
111

11.

Он алтылық санау жүйесі цифрлардан (0, 1, 2, 3, 4, 5,
6, 7, 8, 9) және латын алфавитінің алғашқы үлкен әріптерінен (A, B, C,
D, E, F) тұрады. Негізі 16 санау жүйесі деп те аталады..
10
А
11
В
12
C
13
D
14
E
15
F

12.

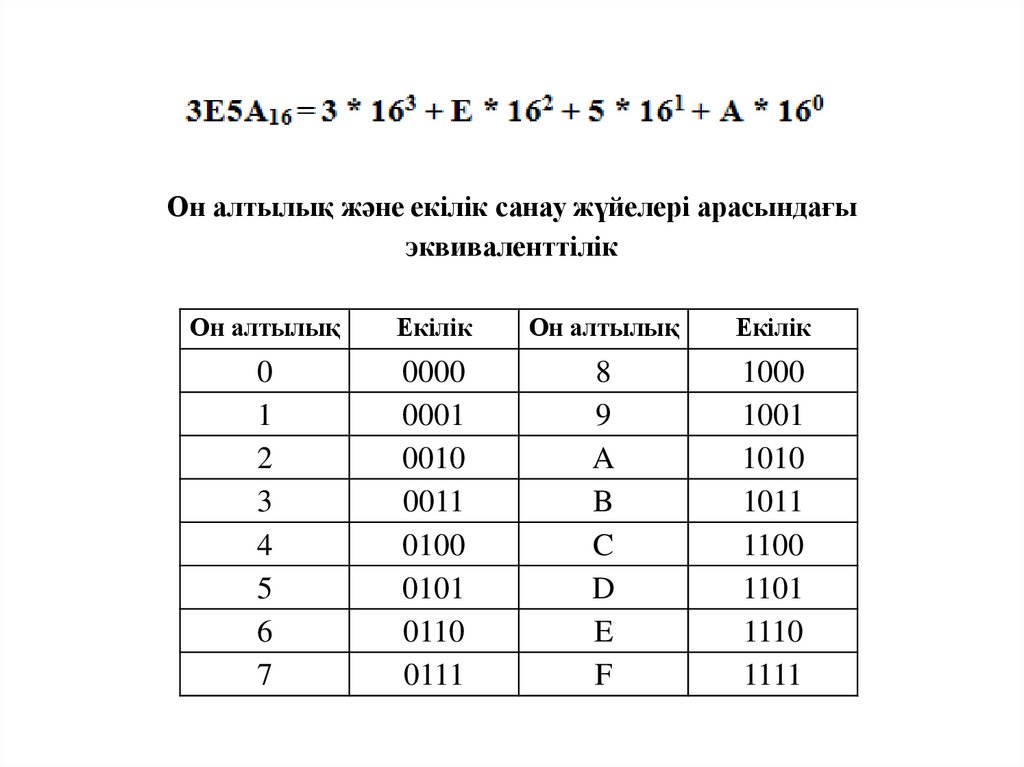
Он алтылық және екілік санау жүйелері арасындағы
эквиваленттілік
Он алтылық
Екілік
Он алтылық
Екілік
0
1
2
3
4
5
6
7
0000
0001
0010
0011
0100
0101
0110
0111
8
9
A
B
C
D
E
F
1000
1001
1010
1011
1100
1101
1110
1111

13.

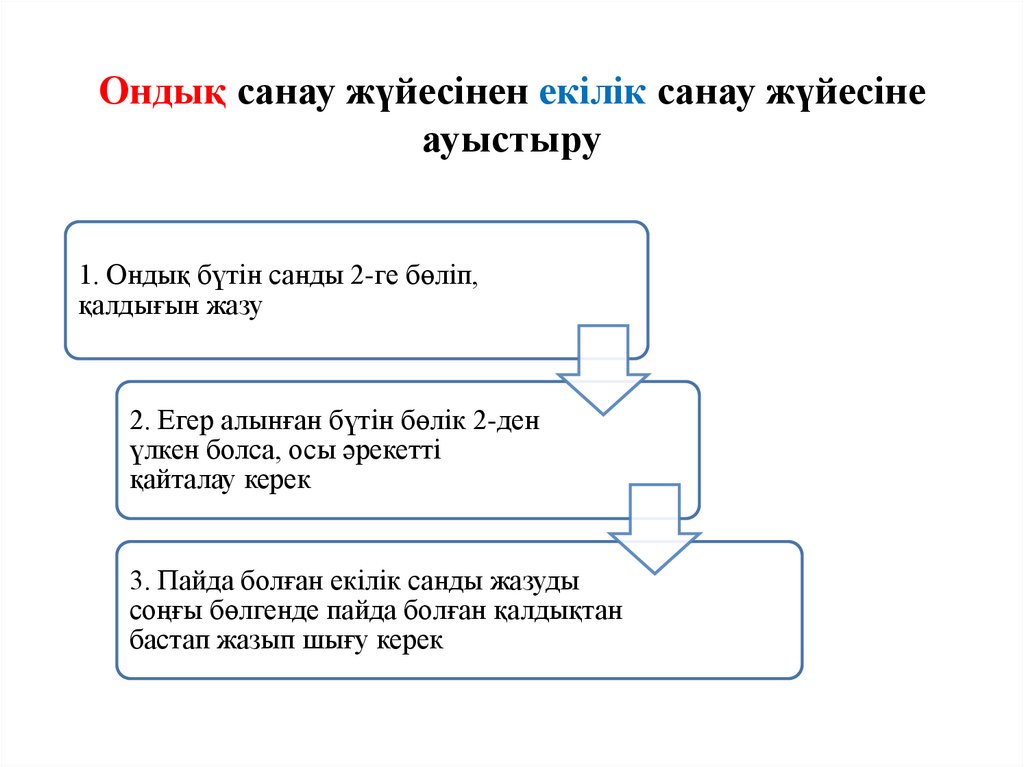
Ондық санау жүйесінен екілік санау жүйесіне
ауыстыру
1. Ондық бүтін санды 2-ге бөліп,
қалдығын жазу
2. Егер алынған бүтін бөлік 2-ден
үлкен болса, осы әрекетті
қайталау керек
3. Пайда болған екілік санды жазуды
соңғы бөлгенде пайда болған қалдықтан
бастап жазып шығу керек

14.

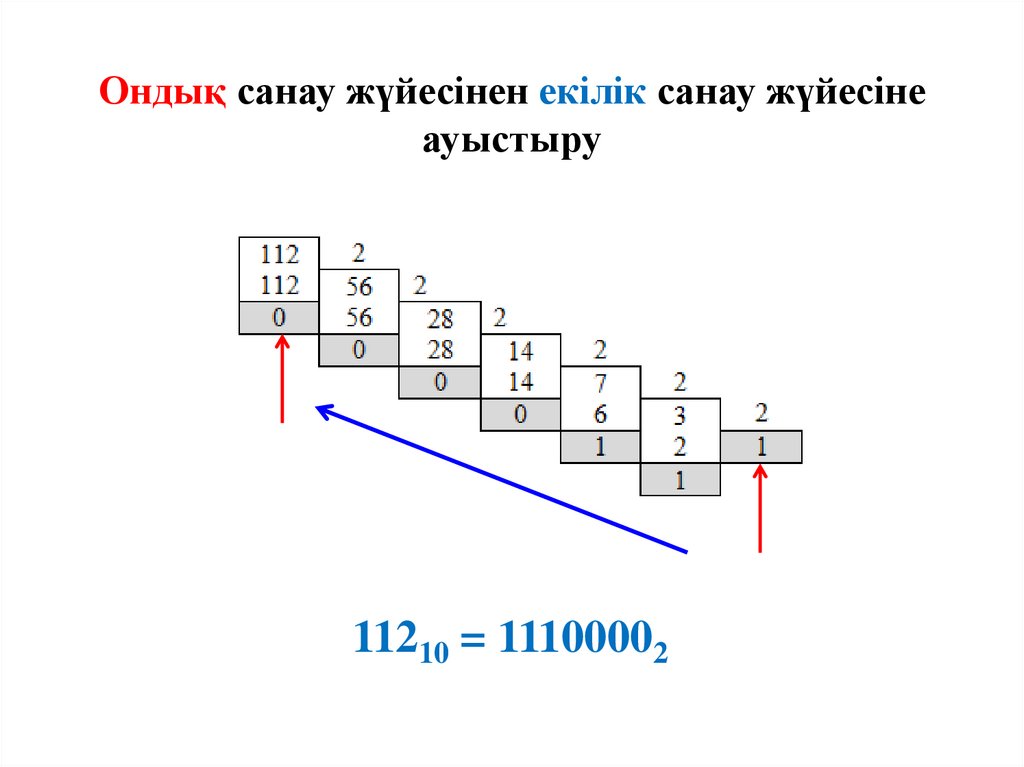
Ондық санау жүйесінен екілік санау жүйесіне
ауыстыру
11210 = 11100002

15.

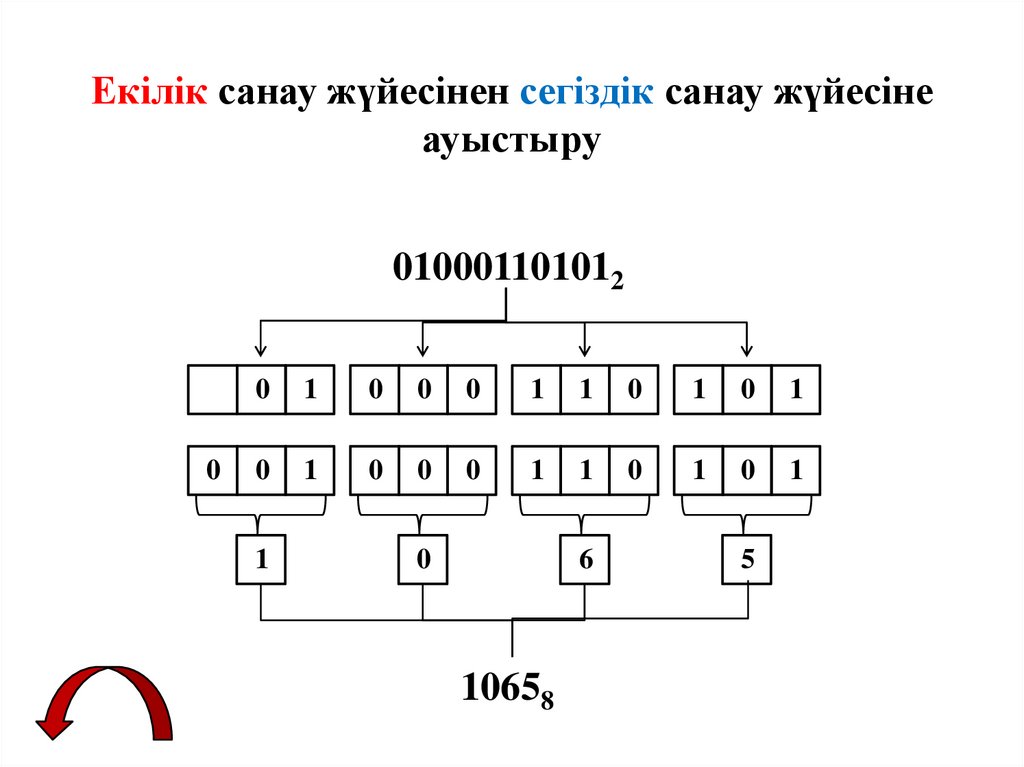
Екілік санау жүйесінен сегіздік санау жүйесіне
ауыстыру
010001101012
0
0
1
0
0
0
1
1
0
1
0
1
0
1
0
0
0
1
1
0
1
0
1
1
0
6
10658
5

16.

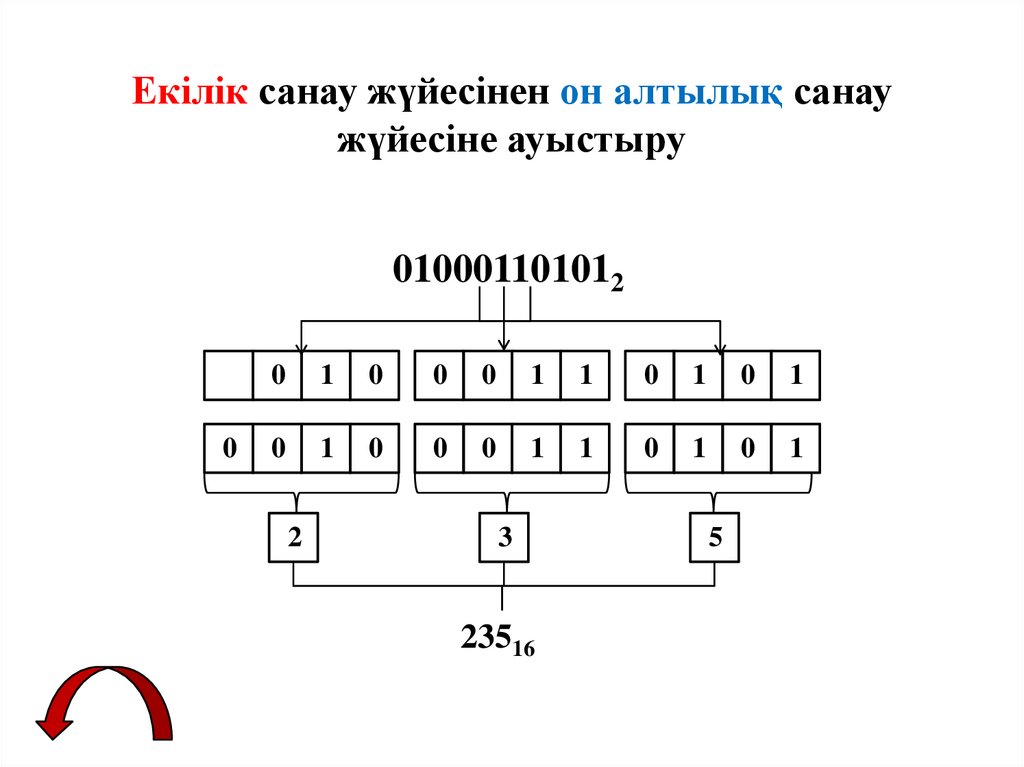
Екілік санау жүйесінен он алтылық санау
жүйесіне ауыстыру
010001101012
0
0
1
0
0
0
1
1
0
1
0
1
0
1
0
0
0
1
1
0
1
0
1
2
3
23516
5

17.

q-негіз → q10
Мысал 1. 101102 → q10
14 03 12 11 00 = 1*24+0*23+1*22+1*21+0*20 = 16+0+4+2+0 = 2210
Мысал 2. 1001.0112 → q10
13 02 01 10, 0-1 1-2 1-3 = 1*23+0*22+0*21+1*20+0*2-1+1*2-2+1*2-3 = 8+2+
1/4 + 1/8 = 9.37510
Мысал 3. 2538 → q10
22 51 30 = 2*82+5*81+3*80 = 2*64+5*8+3*1 = 128+40+3 = 17110

18.

Тапсырма 1.
q-негіз → q10
1) 11111012 = 12510
2) 10011012 = 7710
3) 1110.012
= 14.2510
4) 10111.0012 = 23.12510
5) 1248
= 8410
6) 456,348
= 302.437510
7) 10547
= 38210
8) 30205
= 38510

19.

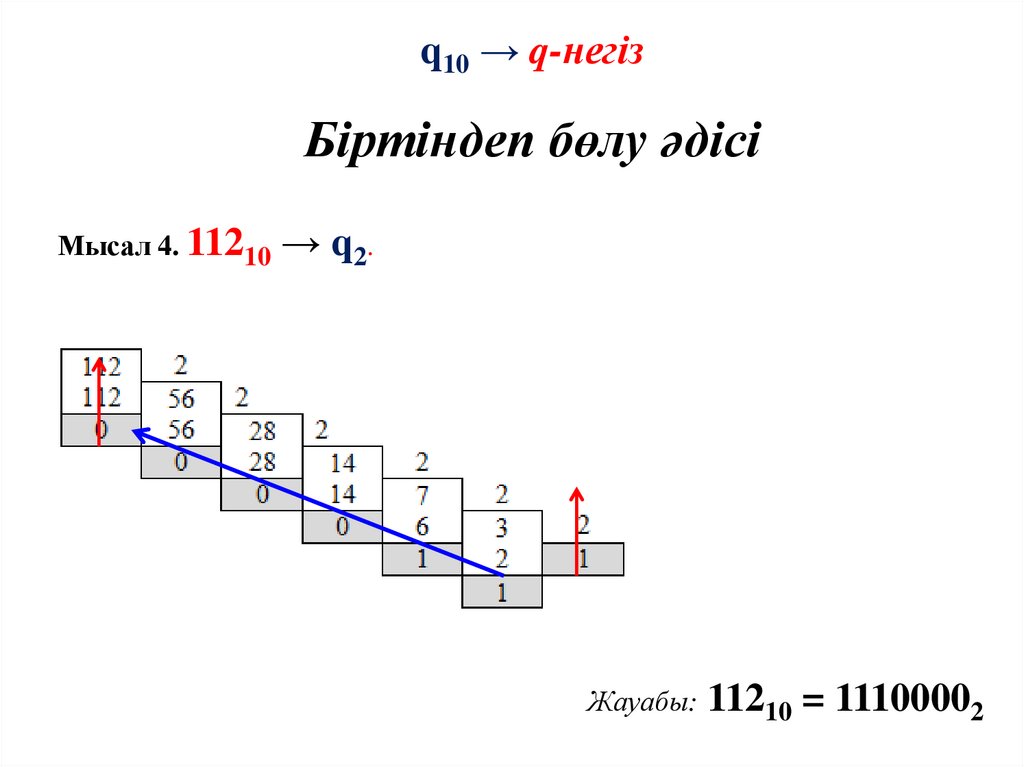
q10 → q-негіз
Біртіндеп бөлу әдісі
Мысал 4. 11210 → q2.
Жауабы: 11210 = 11100002

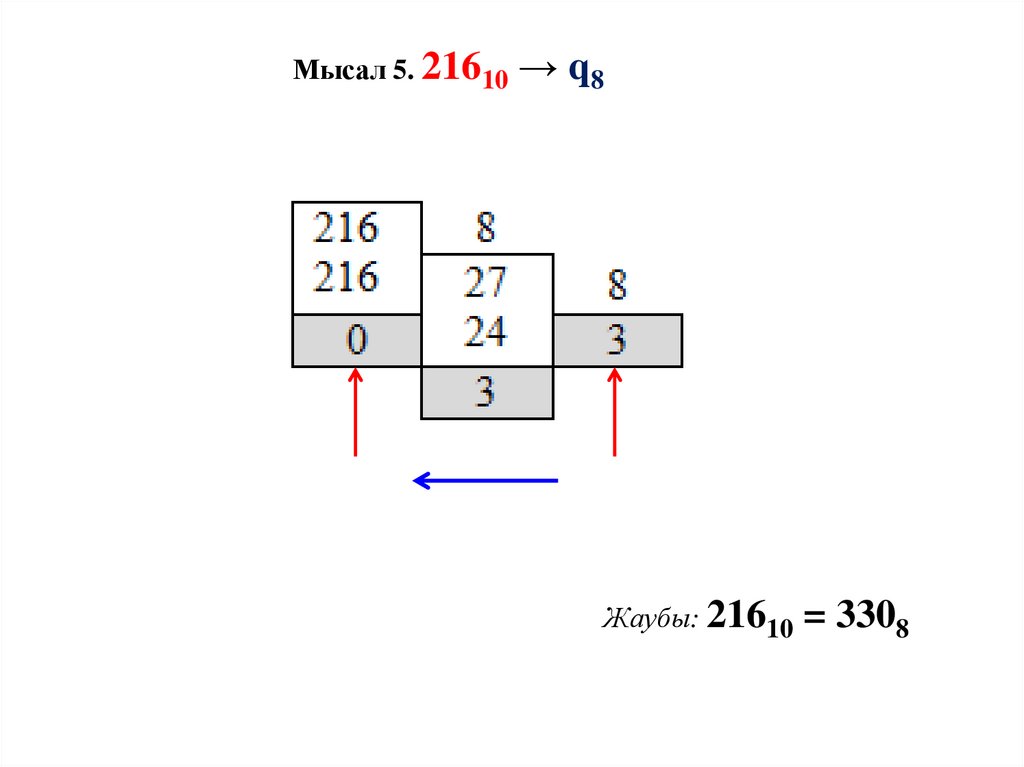
20.

Мысал 5. 21610 → q8
Жаубы: 21610 = 3308

21.

Бөлшек сандарды q10 → басқа санау жүйесіне
ауыстыру
Біртіндеп көбейту әдісі
Мысал 6. 0.8125 q10 → q2:
0.8125 × 2 = 1.625 (1)
0.625 × 2 = 1.25
(1)
0.25 × 2 = 0.5
(0)
0.5 × 2 = 1,0
(1)
Жауабы: 0.812510 = 0.11012

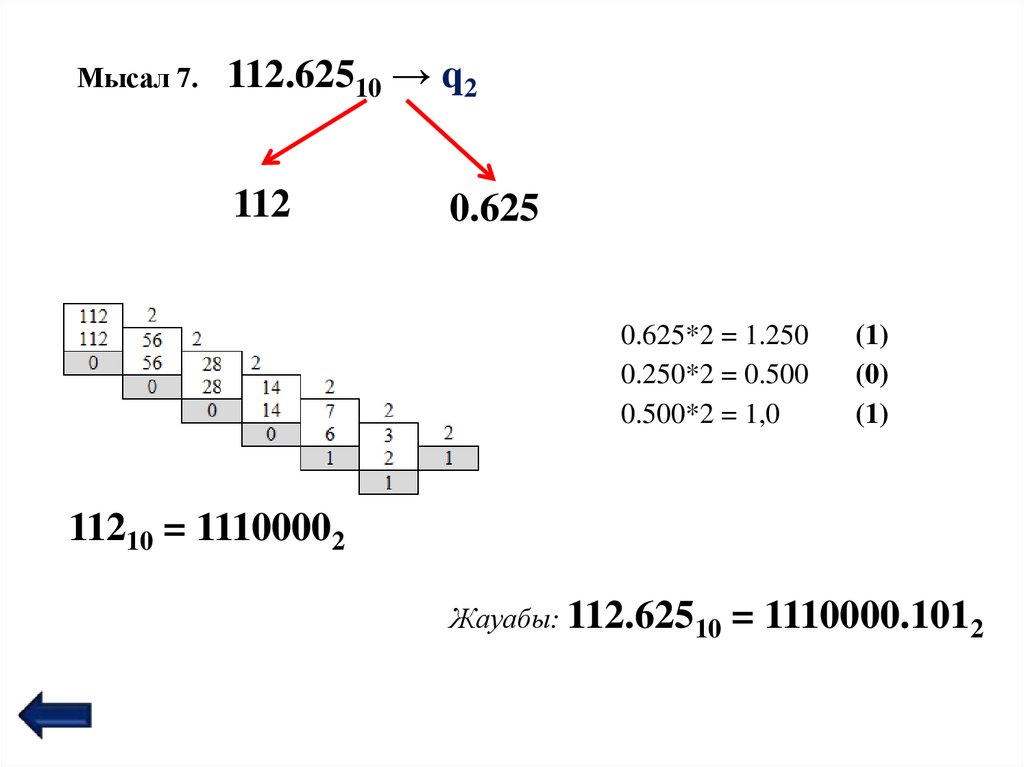
22.

Мысал 7.
112.62510 → q2
112
0.625
0.625*2 = 1.250
0.250*2 = 0.500
0.500*2 = 1,0
(1)
(0)
(1)
11210 = 11100002
Жауабы: 112.62510 = 1110000.1012

23.

Мысал 8.
0.310 → q2.
0.3*2 = 0.6
(0)
0.6*2 = 1.2
(1)
0.2*2 = 0.4
(0)
0.4*2 = 0.8
(0)
0.8*2 = 1.6
(1)
0.6*2 = 1.2
0.2*2 = 0.4
(1)
(0)
0.4*2 = 0.8
0.8*2 = 1.6
(0)
(1)
Жауабы: 0.310 = 0.0(1001)2

24.

Мысал 9.
0.62510 → q8
0.625*8 = 5.0
(5)
Жауабы: 0.62510 = 0.58

25.

Тапсырма 2.
1) 453110→ q2
2) 106710→ q8
3) 55810 → q5
4) 62510 → q3
5) 206.12510 → q2
6) 37,2510 → q2
7) 37.2510 → q16
8) 206.12510 → q8
1) (10001101100112)
2) (20538)
3) (42135)
4) (2120113)
5) (11001110.0012)
6) (100101.012)
7) (25.416)
8) (316.18)

26.

Тапсырма 3
1) 1110011011012 → q8
1) (71558)
2) 101111000111112 → q8
2) (274378)
3) 1010111102 → q16
3) (15E16)
4) 11000112 → q16
4) (6316)

27.

Мысал 10. 3458 → q16
3458 = 0111001012
0111001012 = E516
Жауабы: 3458 = E516

28.

Тапсырма 4.
1) 5008 → q16
1) (14016)
2) 3768 → q16
2)(FE16)
3) 25.418 → q16
3) (15.8416)
4) 7E516 → q8
4) (37458)
5) 3AB16 → q8
5) (16538)

29.

ТАПСЫРМА
Архив файл берілген. Оны ашу үшін құпия сөз қажет. Құпия сөз
алынған санның бөлшек бөлігі болады.
1) 7,62510 → q2
2) 2,12510 → q2
3) 17,2510 → q2
4) 6,187510 → q2
5) 5,62510 → q2
6) 3,7510 → q2
7) 13,2510 → q2
8) 10,062510 → q2
9) 2,562510 → q2
10) 3,687510 → q2
11) 5,37510 → q2
12) 7,812510 → q2
13) 9,23510 → q2
14) 25,70310 → q2
15) 5,8510 → q2
16) 7.2810 → q2
17) 3,6510 → q2
18) 14,510 → q2
19) 7,4510 → q2
20) 3,90510 → q2
21) 2,84510 → q2
22) 3,50510 → q2
23) 4,10510 → q2
24) 5,9910 → q2
25) 7,6810 → q2
26) 2,60110 → q2