Similar presentations:
Л 4 Законы сохранения в механике
1. Законы сохранения в механике
Преподаватель:к.т.н. Богатырева Жанна Игоревна
2.
Импульс тела3.
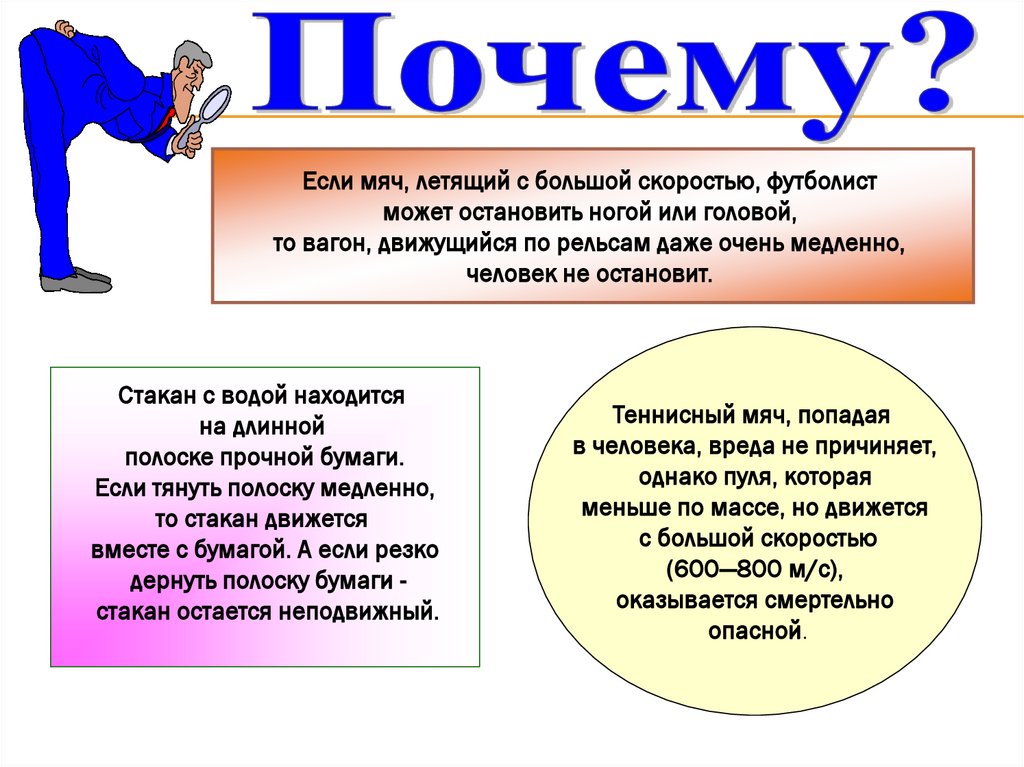
Если мяч, летящий с большой скоростью, футболистможет остановить ногой или головой,
то вагон, движущийся по рельсам даже очень медленно,
человек не остановит.
Стакан с водой находится
на длинной
полоске прочной бумаги.
Если тянуть полоску медленно,
то стакан движется
вместе с бумагой. А если резко
дернуть полоску бумаги стакан остается неподвижный.
Теннисный мяч, попадая
в человека, вреда не причиняет,
однако пуля, которая
меньше по массе, но движется
с большой скоростью
(600—800 м/с),
оказывается смертельно
опасной.
4. СИЛА И СКОРОСТЬ
• Задача механики – описание движениятел, решается с помощью II з. Ньютона.
Существуют случаи, когда силу невозможно
измерить, например, столкновения тел.
• Тогда удобнее рассчитывать изменение
скорости тел, т.к. сила вызывает изменение
скорости. Движение тел до удара и после
удара будем считать равномерными.
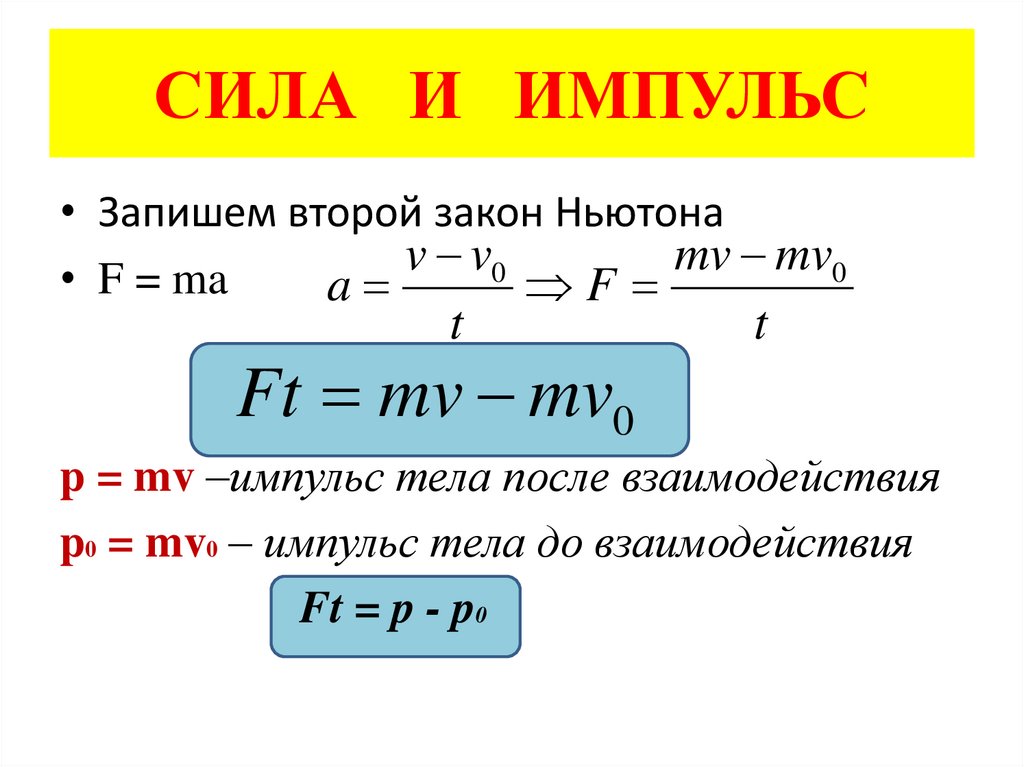
5. СИЛА И ИМПУЛЬС
• Запишем второй закон Ньютонаv
v
mv
mv
0
0
• F = ma
a
F
t
Ft mv mv0
t
p = mv –импульс тела после взаимодействия
p0 = mv0 – импульс тела до взаимодействия
Ft = p - p0
6.
Изменение импульса тела происходит привзаимодействии тел. Например, при ударах.
7. ИМПУЛЬС ТЕЛА
– произведение массы тела на егоскорость.
Импульс – векторная величина,
направление импульса совпадает с
направлением скорости.
Единица измерения импульса кг·м/с
Если тело покоится , то импульс
равен нулю
8.
9.
10.
Импульс – это векторная величина.Направление вектора импульса
тела всегда совпадает с
направлением вектора скорости
движения.
11.
Слово «импульс»(impulsus) в переводе с
латинского означает
«толчок»
Эта величина была введена в
науку в конце XVII века
12. ЗАДАЧА
• Шарик массой 100г, летящий со скоростью20м/с, упруго ударяется о стенку и отскакивает
от нее с такой же скоростью.
Найти изменение импульса шарика
Решение
p1
mv
Δp = p2 – p1 = mv – (- mv) =
-mv
p2
= 2mv
Δp = 2·0,1·20 = 4кг·м/с
13. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Сумма импульсов тел до взаимодействияравна сумме импульсов тел после
взаимодействия
m1v1 + m2v2 = m1u1 + m2u2
В задачах рассматривается система из двух
тел, внешние силы отсутствуют
(замкнутая система)
14.
Векторная сумма импульсовтел, составляющих замкнутую
систему, не меняется с
течением времени при любых
движениях и взаимодействия
этих тел.
15.
ЗАМКНУТАЯ СИСТЕМАЭТО СИСТЕМА ТЕЛ,
КОТОРЫЕ
ВЗАИМОДЕЙСТВУЮТ
ТОЛЬКО ДРУГ С ДРУГОМ
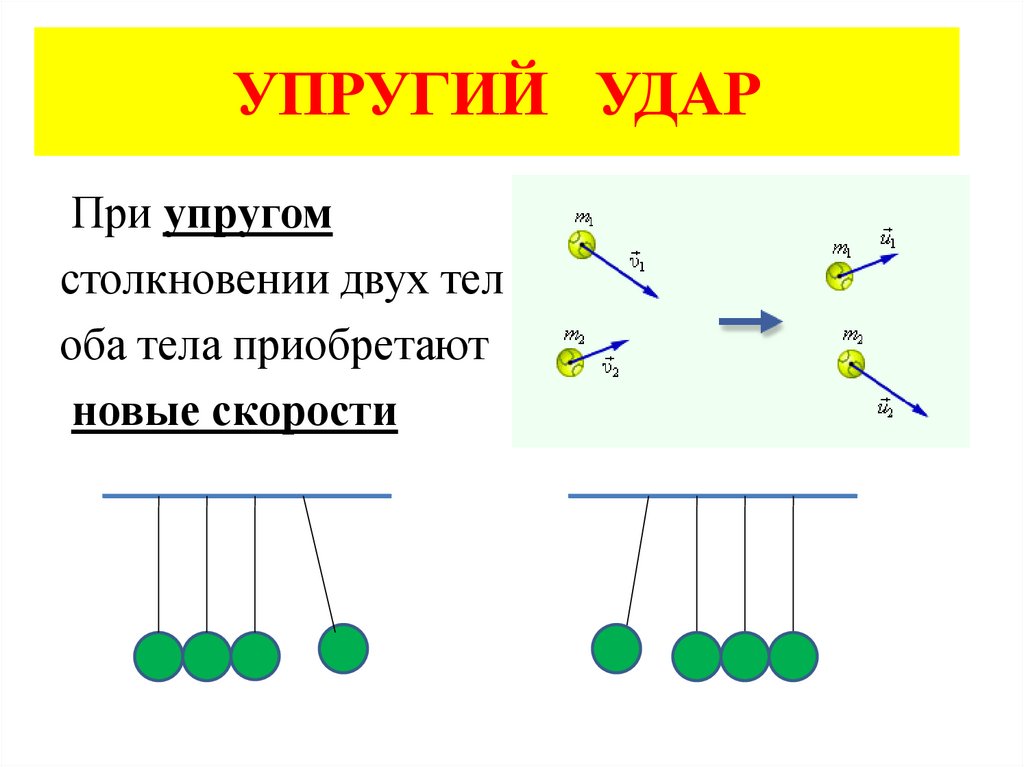
16. УПРУГИЙ УДАР
При упругомстолкновении двух тел
оба тела приобретают
новые скорости
17.
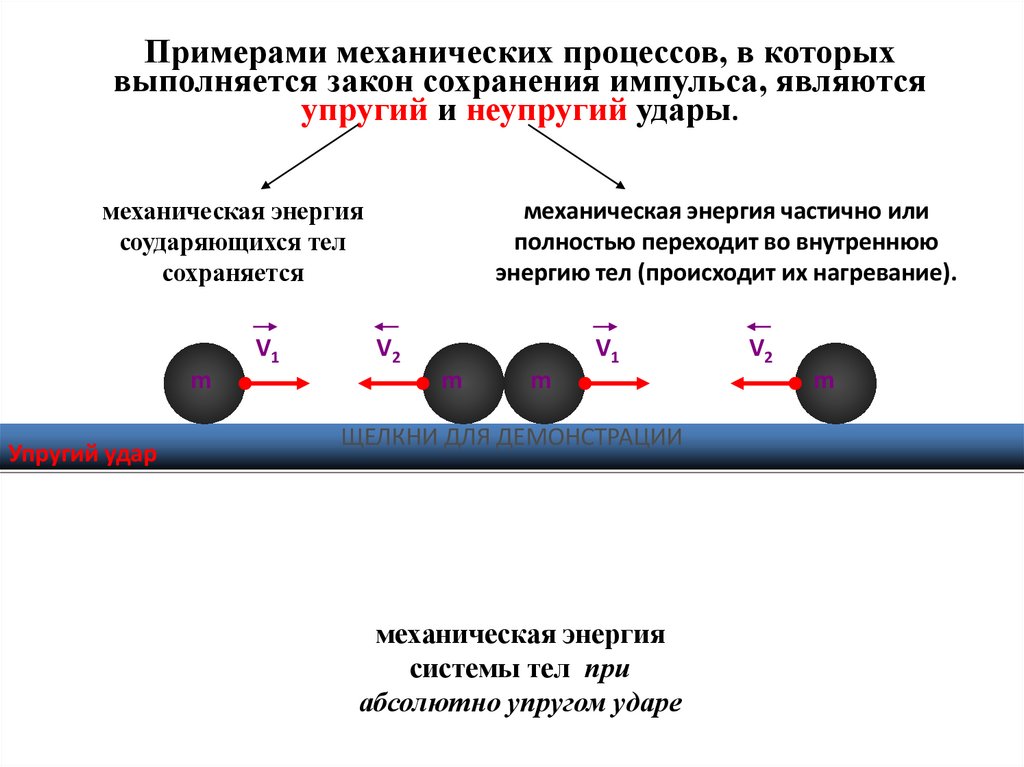
Примерами механических процессов, в которыхвыполняется закон сохранения импульса, являются
упругий и неупругий удары.
механическая энергия
соударяющихся тел
сохраняется
V1
m
Упругий удар
механическая энергия частично или
полностью переходит во внутреннюю
энергию тел (происходит их нагревание).
V2
V1
m
m
ЩЕЛКНИ ДЛЯ ДЕМОНСТРАЦИИ
механическая энергия
системы тел при
абсолютно упругом ударе
V2
m
18. НЕУПРУГИЙ УДАР
• При неупругом ударе тела соединяются ипосле удара движутся вместе.
• Уравнение закона сохранения импульса
имеет вид
m1v1 ± m2v2 = (m1 + m2 )u
• (если тела движутся навстречу друг
другу, то ставится «-», если одно тело
догоняет другое, то ставится «+»)
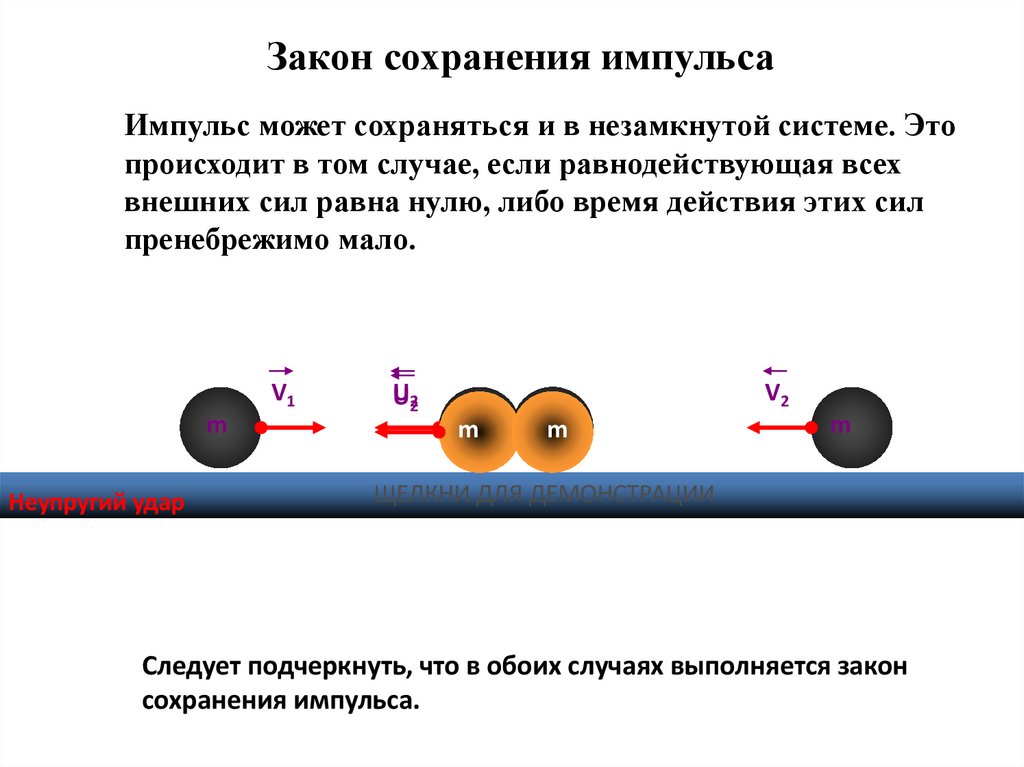
19. Закон сохранения импульса
Импульс может сохраняться и в незамкнутой системе. Этопроисходит в том случае, если равнодействующая всех
внешних сил равна нулю, либо время действия этих сил
пренебрежимо мало.
V1
m
Неупругий удар
U22
V2
m
m
m
ЩЕЛКНИ ДЛЯ ДЕМОНСТРАЦИИ
Следует подчеркнуть, что в обоих случаях выполняется закон
сохранения импульса.
20. РЕАКТИВНОЕ ДВИЖЕНИЕ
– движение тела при отделении от негонекоторой массы
0 = m1v1 - m2v2 или m1v1 = m2v2
Например: а) выстрел из ружья
б) полет ракеты
? Зачем нужно прижимать приклад ружья к
плечу в момент выстрела?
21. Примеры применения закона сохранения импульса
Примеры применения закона сохранения• Закон строго выполняется в
импульса
явлениях отдачи при
выстреле, явлении
реактивного движения,
взрывных явлениях и
явлениях столкновения тел.
• Закон сохранения импульса
применяют: при расчетах
скоростей тел при взрывах и
соударениях; при расчетах
реактивных аппаратов; в
военной промышленности
при проектировании
оружия; в технике - при
забивании свай, ковке
металлов и т.д.
22.
Применение закона сохранения импульсаВ природе
Осьминоги вбирают в себя воду и затем
резко выбрасывают её, получая при этом
импульс, направленный в противоположную
сторону. Управляя струёй, осьминог может
двигаться в нужном направлении
В технике
Движение ракет
23. ЗАДАЧА
• Летящая пуля массой 10гударяется в брусок массой 390г
и застревает в нем. Найти
скорость бруска, если скорость
пули 200м/с.
24. ЗАДАЧА
• Дано:СИ
Решение
m1 = 10г
0,01кг
ЗСИ для неупругого удара
m2 = 390г 0,39кг m1v1 ± m2v2 = (m1 + m2 )u
v1 = 200м/с
m1v1 = (m1 + m2 )u
m1v1
v2 = 0
u
m1 m2
u-?
0,01 200
2
u
5м / с
0,39 0,01 0,4
25.
Работа силы.Мощность
26.
В каких случаях совершаетсямеханическая работа?
Механическая работа
совершается,
только когда на тело
действует сила и оно
движется
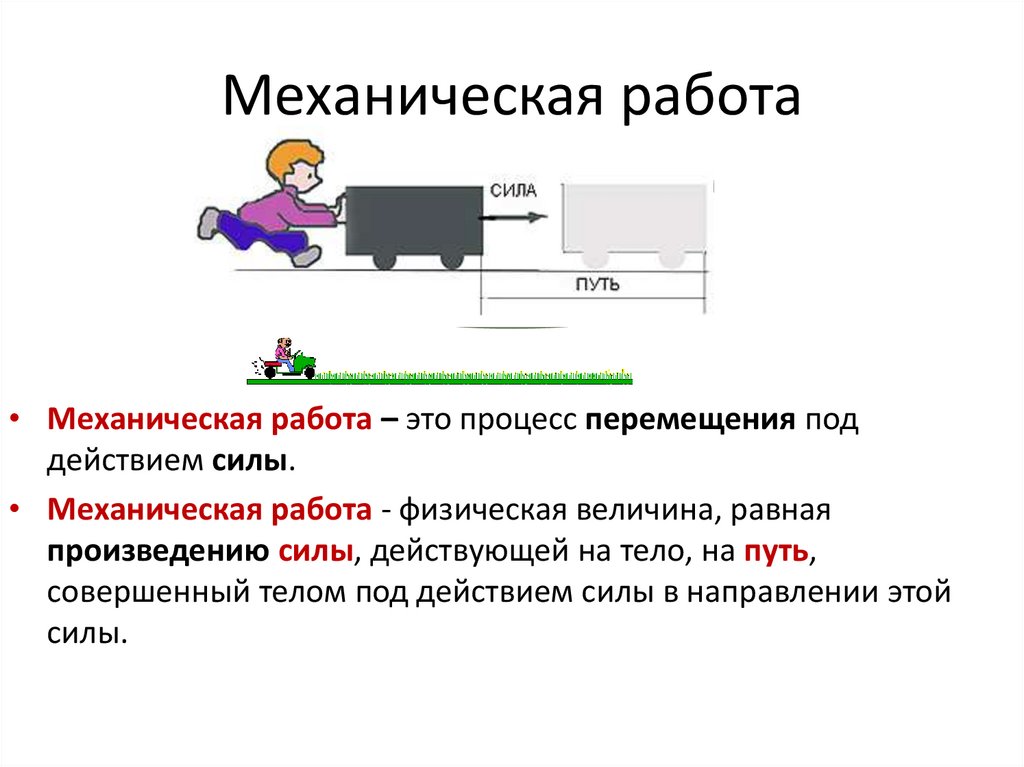
27. Механическая работа
СилаПуть
Работа
• Механическая работа – это процесс перемещения под
действием силы.
• Механическая работа - физическая величина, равная
произведению силы, действующей на тело, на путь,
совершенный телом под действием силы в направлении этой
силы.
28.
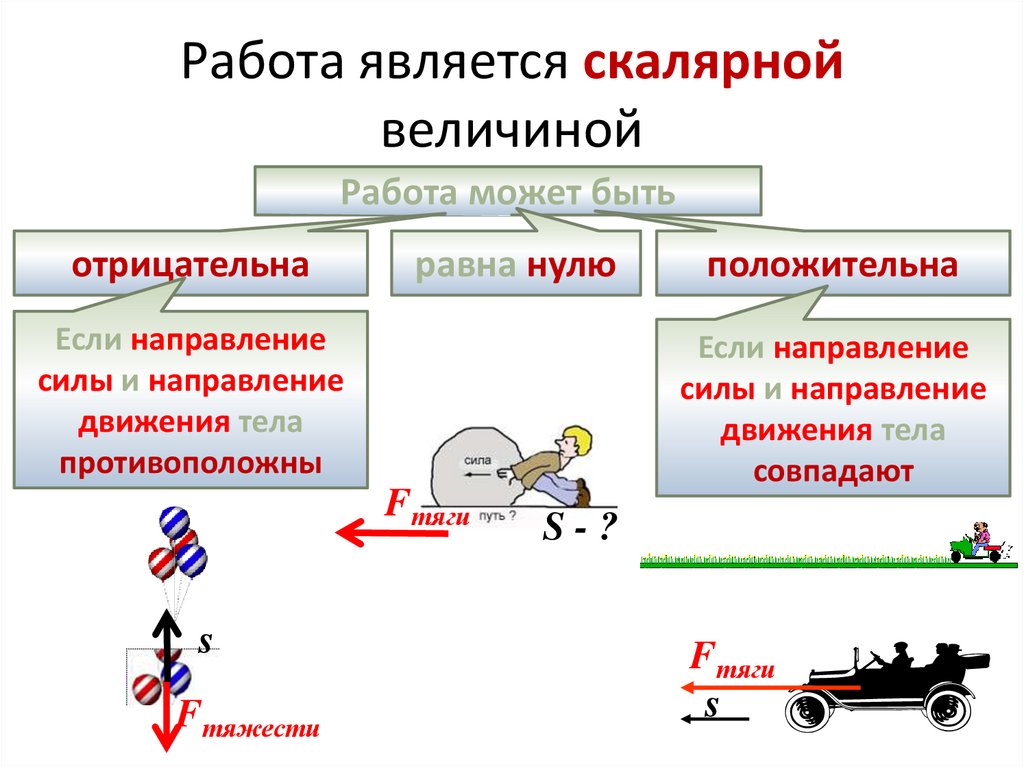
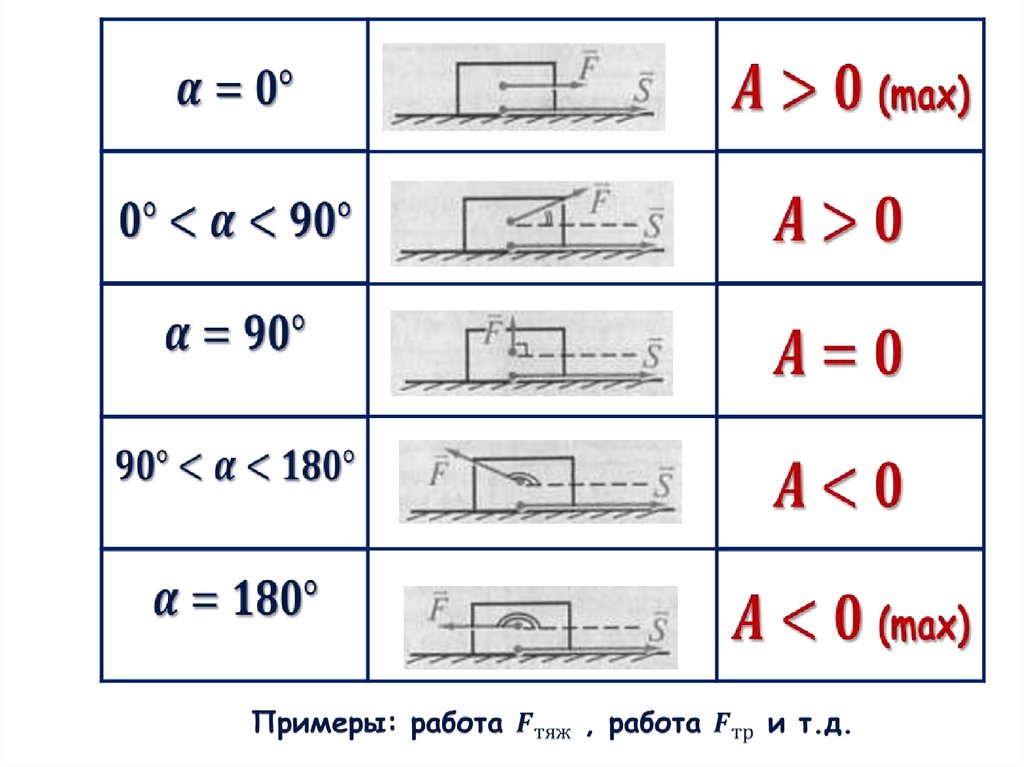
Определение, формула работы29. Работа является скалярной величиной
Работа может бытьотрицательна
равна нулю
Если направление
силы и направление
движения тела
противоположны
Fтяги
s
Fтяжести
положительна
Если направление
силы и направление
движения тела
совпадают
S-?
Fтяги
s
30.
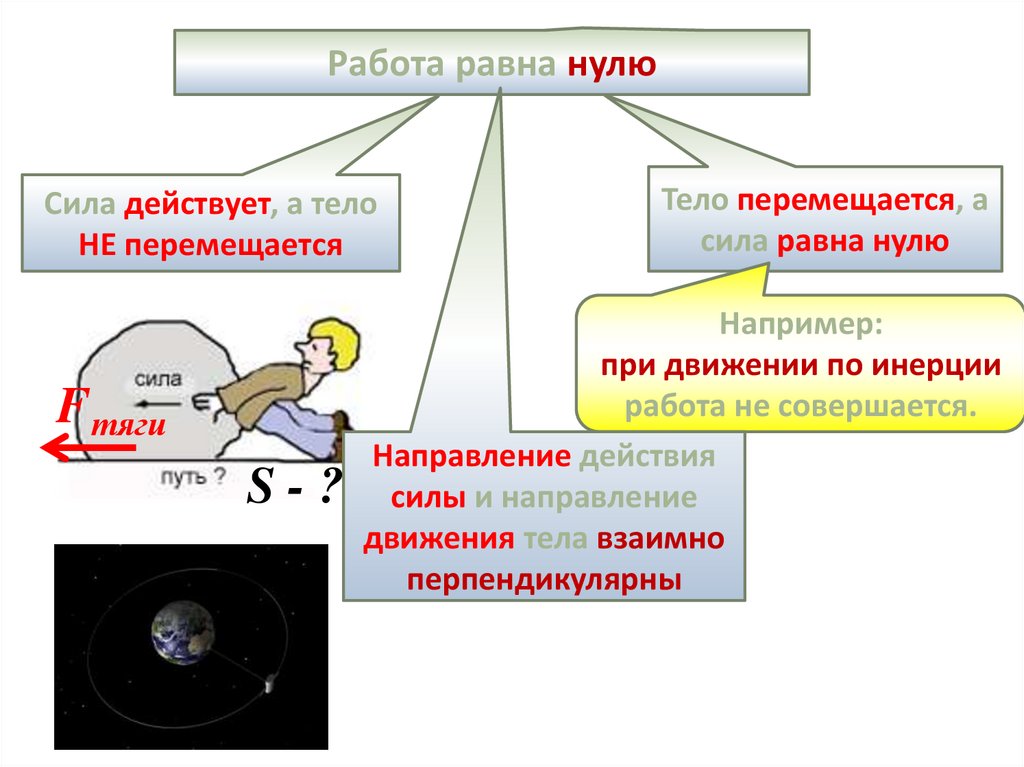
Работа равна нулюСила действует, а тело
НЕ перемещается
Fтяги
Тело перемещается, а
сила равна нулю
Например:
при движении по инерции
работа не совершается.
Направление действия
S - ? силы и направление
движения тела взаимно
перпендикулярны
31.
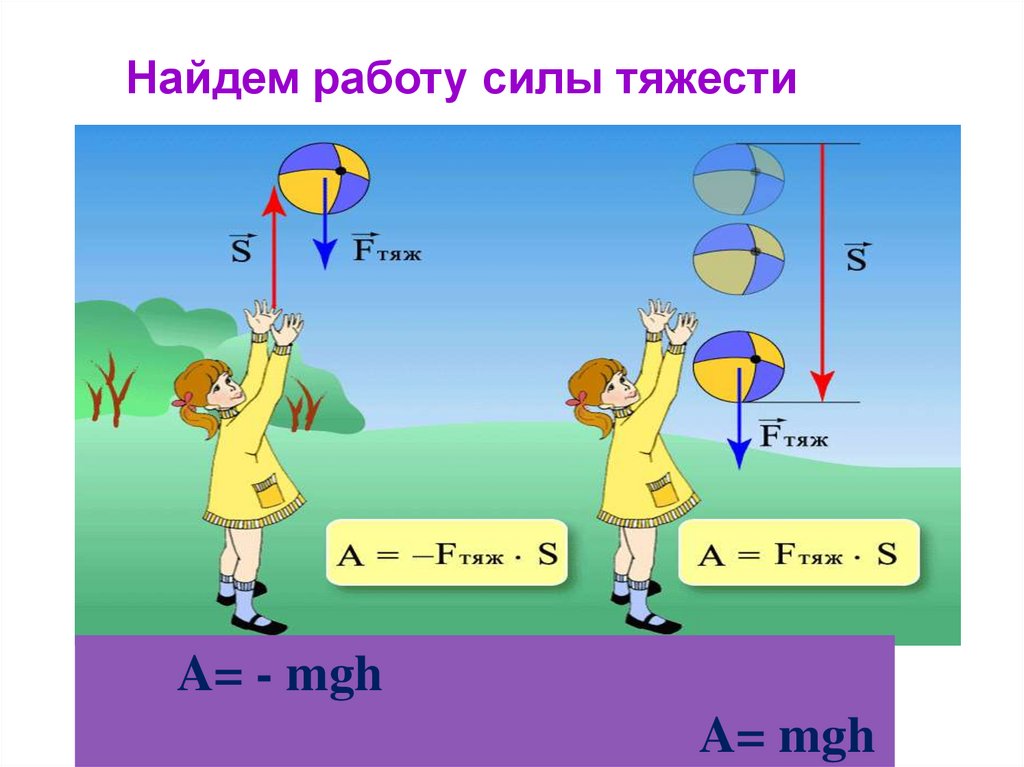
Найдем работу силы тяжестиA= - mgh
A= mgh
32.
33.
1 Дж = 1 Н · 1 м = 1 Н · мДжеймс ДЖОУЛЬ
1818 г. – 1889 г.
Джоуль – это работа,
совершаемая силой
1 Н на перемещении 1 м,
если направления силы и
перемещения совпадают
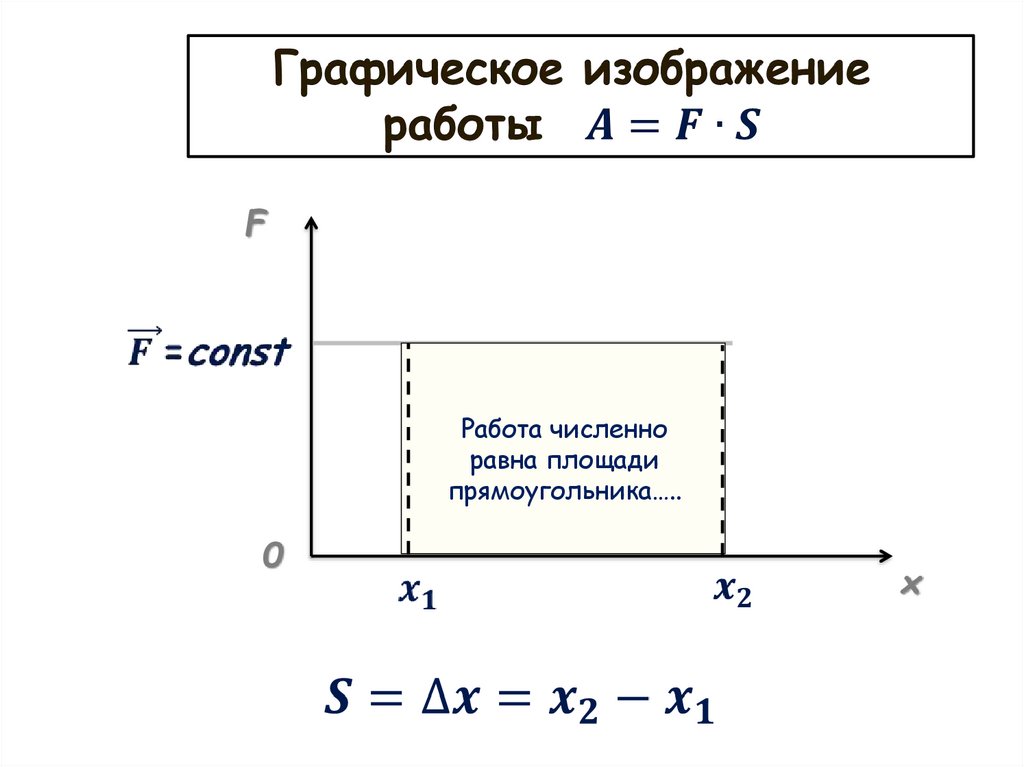
34.
FРабота численно
равна площади
прямоугольника…..
0
x
35.
Работа силы тяжести1
2
1
2
2
1
36.
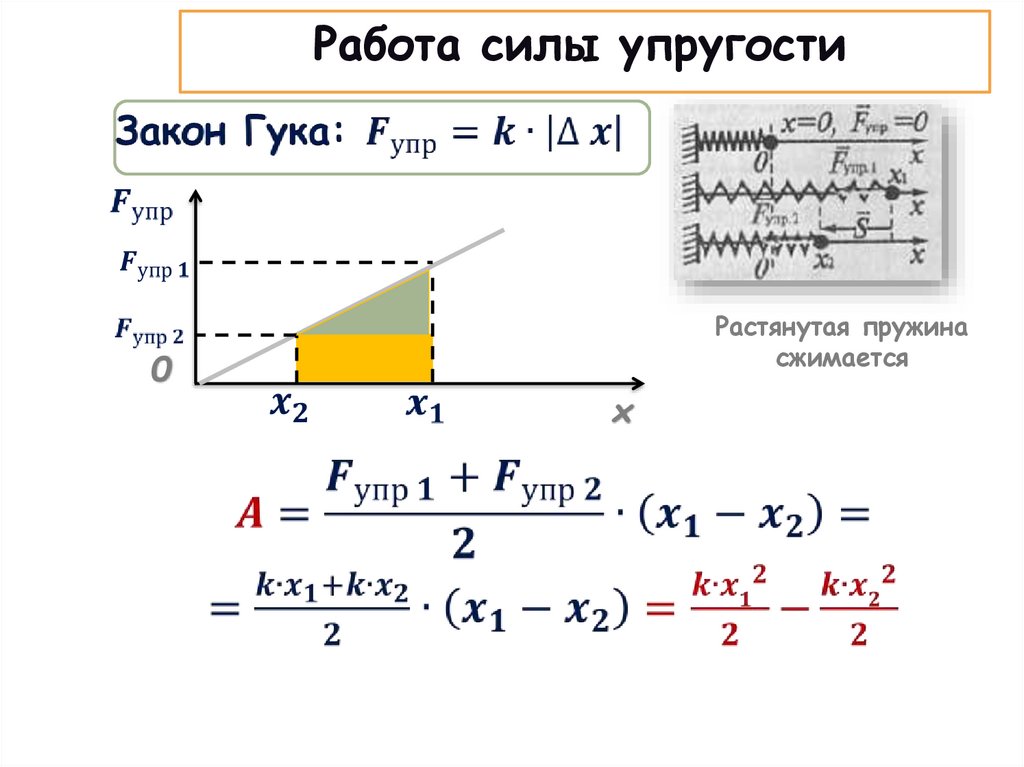
Работа силы упругости0
Растянутая пружина
сжимается
x
37.
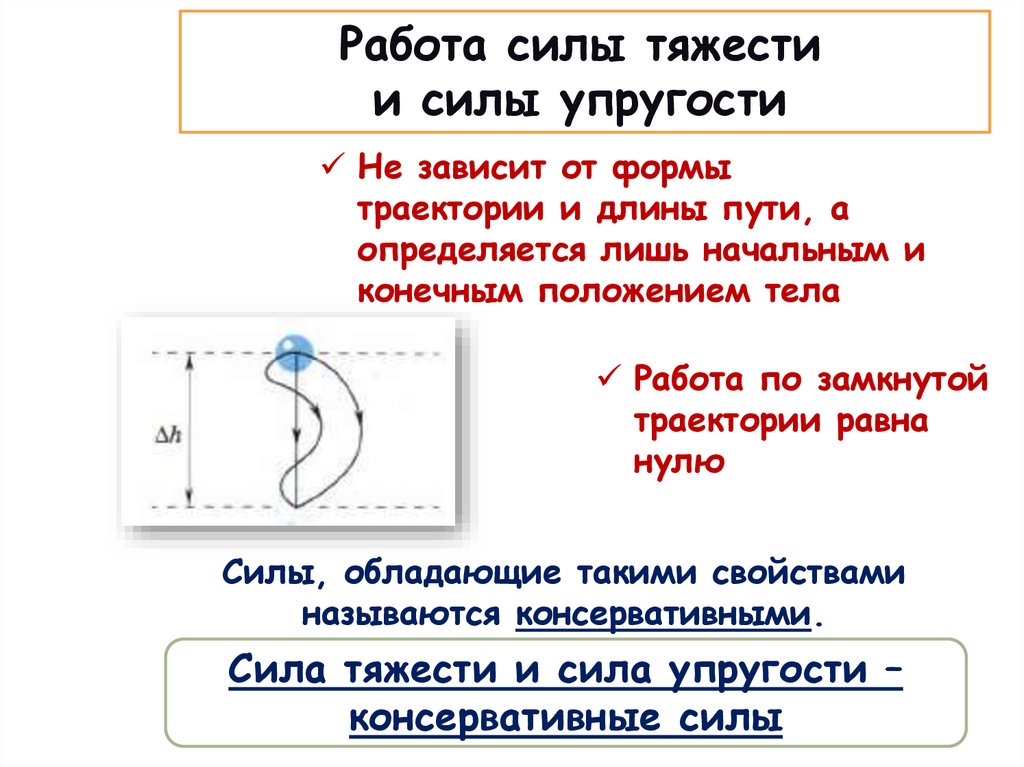
Работа силы тяжестии силы упругости
Не зависит от формы
траектории и длины пути, а
определяется лишь начальным и
конечным положением тела
Работа по замкнутой
траектории равна
нулю
Силы, обладающие такими свойствами
называются консервативными.
Сила тяжести и сила упругости –
консервативные силы
38.
МОЩНОСТЬN – мощность, физическая величина,
характеризующая «быстроту» совершения
работы.
39.
Мощность численно равна работе,совершенной в единицу времени
40.
Потенциальная икинетическая
энергия
41. 2
Энергия является сложным понятием, связанная спонятиями: «работа» и «движение»
Способность совершать работу
обладают тела, которые
находятся в движении
42.
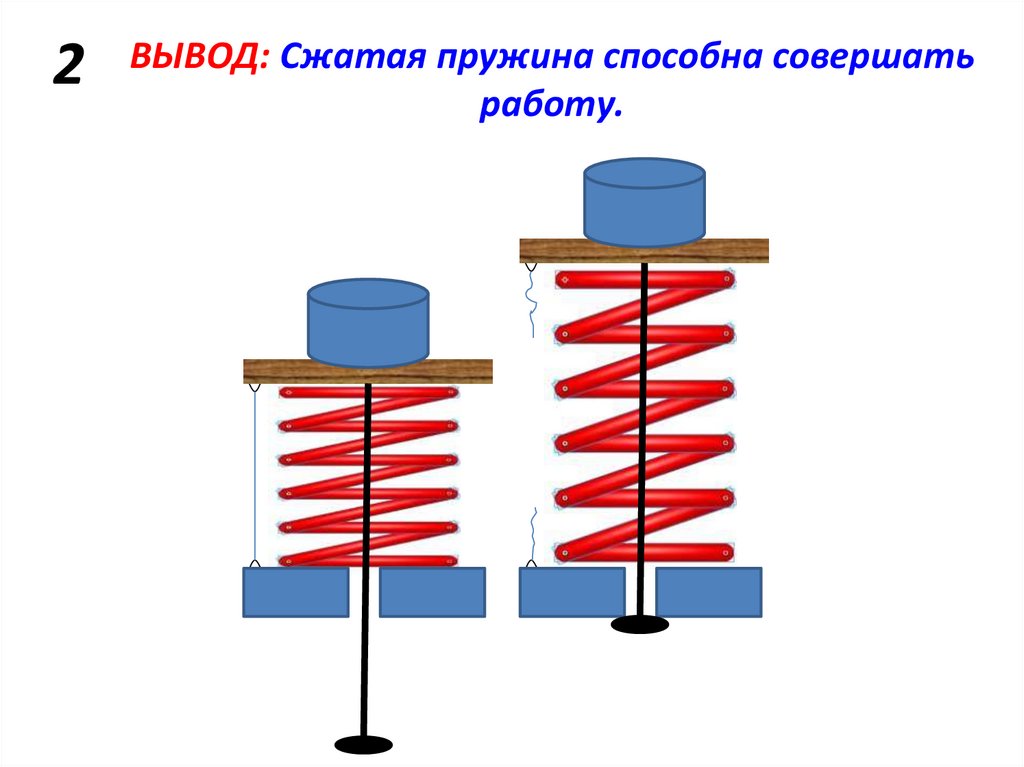
2ВЫВОД: Сжатая пружина способна совершать
работу.
43.
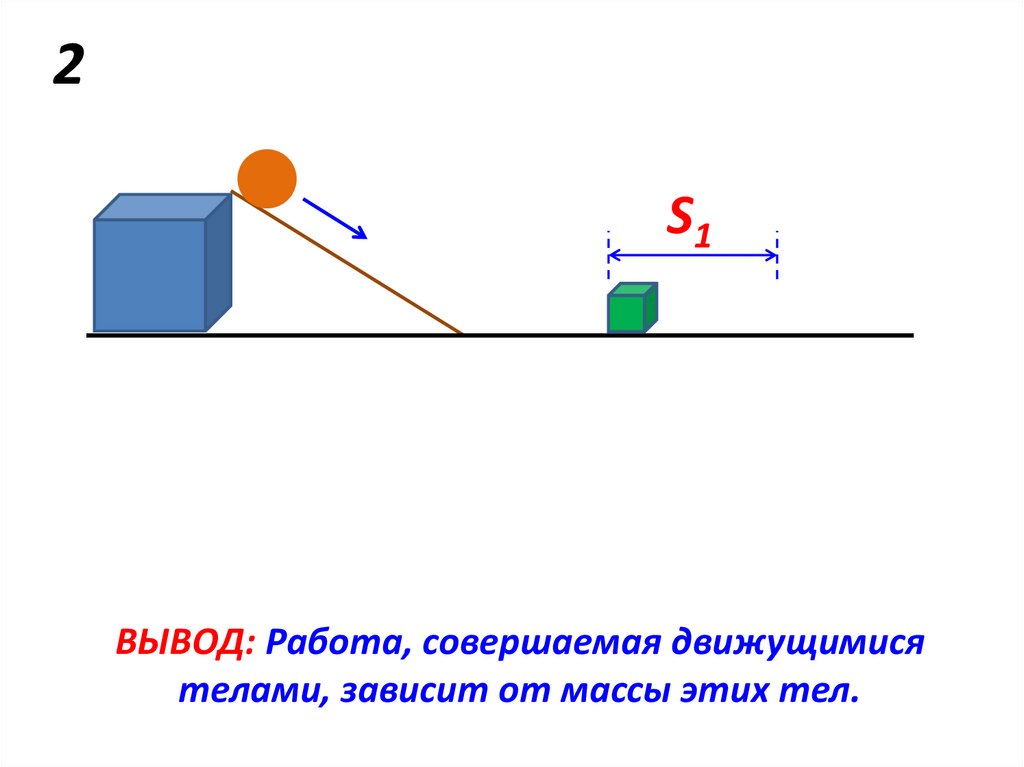
2S1
S2
ВЫВОД: Работа, совершаемая движущимися
телами, зависит от массы этих тел.
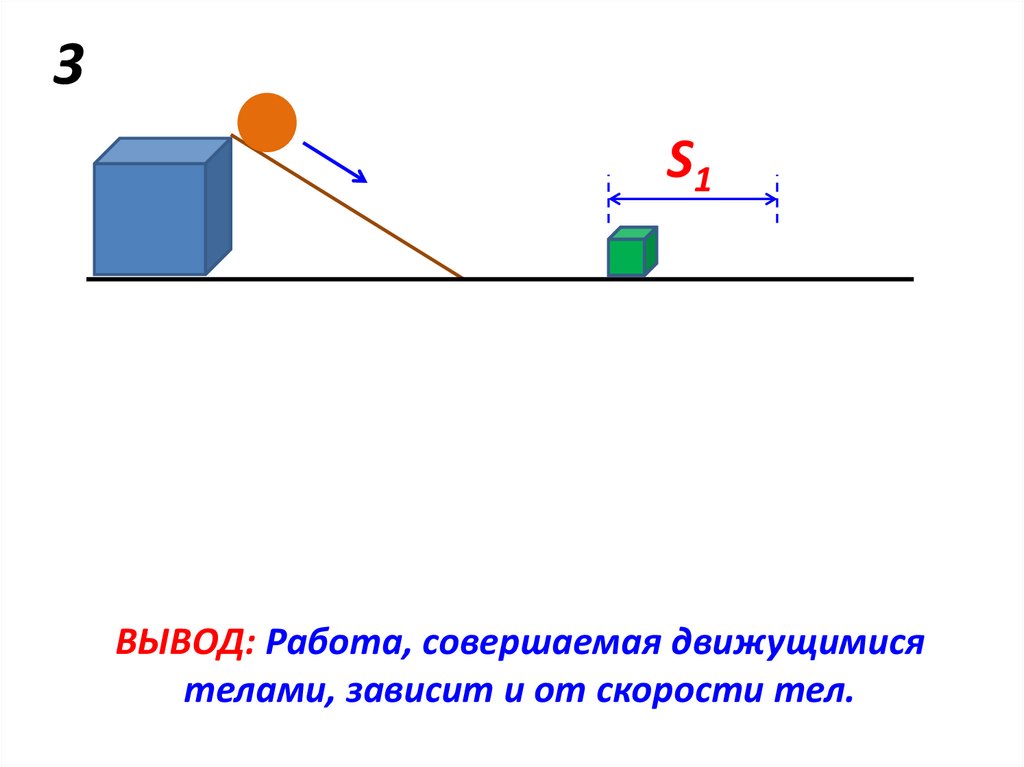
44. 3
S1S2
ВЫВОД: Работа, совершаемая движущимися
телами, зависит и от скорости тел.
45. 4
ОБЩИЙ ВЫВОД: работа, совершаемаядвижущимися телами, зависит от массы
тел и от его скорости.
Физическая величина, характеризующая
способность тела совершать работу,
называется энергией.
Обозначение и единицы измерения энергии:
[Е] = Джоуль
46.
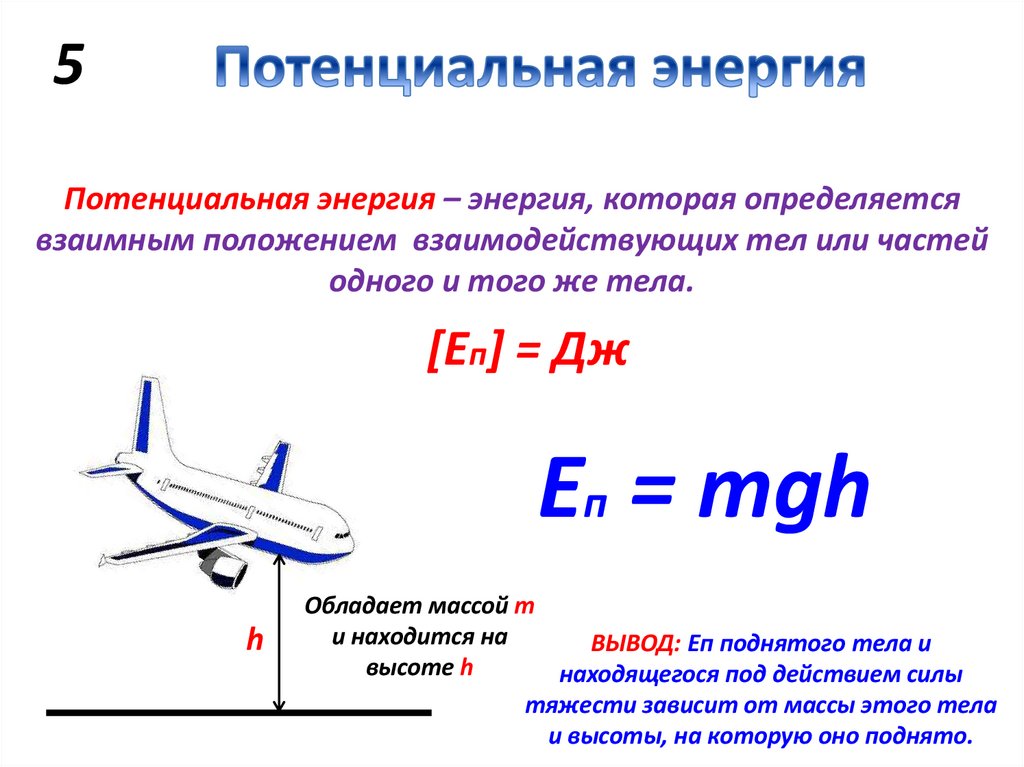
5Потенциальная энергия – энергия, которая определяется
взаимным положением взаимодействующих тел или частей
одного и того же тела.
[Еп] = Дж
Еп = mgh
h
Обладает массой m
и находится на
ВЫВОД: Еп поднятого тела и
высоте h
находящегося под действием силы
тяжести зависит от массы этого тела
и высоты, на которую оно поднято.
47.
Потенциальной энергией обладает такжедеформированное тело. Заведённая пружина
за счёт энергии приводит в движение часовой
механизм и совершает тем самым работу.
48.
Деформированный лук совершает работу, сообщаястреле скорость
49.
6Кинетическая энергия – энергия, которой обладает тело
вследствие своего движения.
[Ек] = Дж
mv2
Ек = 2
Обладает массой m
и скоростью v
ВЫВОД: Ек как и работа, изменяется в
зависимости от массы и скорости тел.
50.
У какого изэтих
двигающихся
тел
кинетическая
энергия
больше?
У самолёта
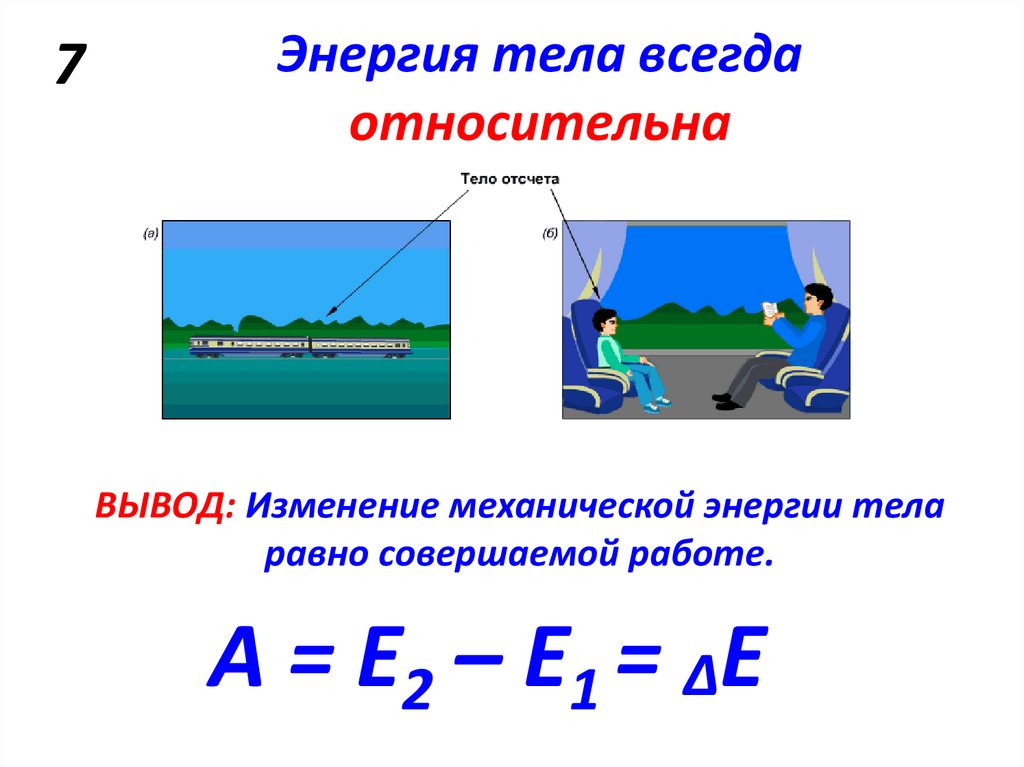
51. 7
Энергия тела всегдаотносительна
ВЫВОД: Изменение механической энергии тела
равно совершаемой работе.
А = Е2 – Е1 = ∆Е
52. ИЗУЧЕНИЕ ЯВЛЕНИЙ ПРЕВРАЩЕНИЯ ОДНОГО ВИДА ЭНЕРГИИ В ДРУГОЙ ПРИВЕЛО К ОТКРЫТИЮ ОДНОГО ИЗ ОСНОВНЫХ ЗАКОНОВ ПРИРОДЫ – ЗАКОНА
СОХРАНЕНИЯ ИПРЕВРАЩЕНИЯ ЭНЕРГИИ
ВО ВСЕХ ЯВЛЕНИЯХ,
ПРОИСХОДЯЩИХ В ПРИРОДЕ,
ЭНЕРГИЯ НЕ ВОЗНИКАЕТ И НЕ
ИСЧЕЗАЕТ, ОНА ТОЛЬКО
ПРЕВРАЩАЕТСЯ ИЗ ОДНОГО ВИДА
В ДРУГОЙ, ПРИ ЭТОМ ЕЁ ЗНАЧЕНИЕ
СОХРАНЯЕТСЯ.
53. Закон сохранения механической энергии
Сумма кинетической и потенциальнойэнергии тел, составляющих замкнутую
систему и взаимодействующих между
собой силами тяготения и силами
упругости, остается неизменной.
Сумму E = Ek + Ep называют полной
механической энергией
54. Закон сохранения и превращения механической энергии
Одним из следствий закона сохранения ипревращения энергии является
утверждение о невозможности создания
«вечного двигателя» (perpetuum mobile)
– машины, которая могла бы
неопределенно долго совершать работу, не
расходуя при этом энергии




































 physics
physics








