Similar presentations:
урок 26 алгебра 10 класс формула полной верояности и Байеса
1.
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИФОРМУЛА БАЙЕСА
2.
1 урок3.
Цели обучения10.3.2.5 знать формулу полной вероятности и
применять ее при решении задач;
4.
Цель урокарассмотреть применение формулы полной
вероятности при решении задач.
5.
Формула полной вероятности является следствиемтеорем сложения и умножения вероятностей. Она
позволяет определять вероятность некоторого
события, которое может происходить в различных
ситуациях с разной вероятностью, причем
вероятности этих ситуаций можно оценить до опыта,
а условные вероятности появления рассматриваемого
события при каждой сложившейся ситуации должны
быть известны.
6. Формула полной вероятности
Пусть события В1 ,В2 , … , Вn образуют полнуюгруппу событий и при наступлении каждого из них,
например Вi , событие А может наступить с
некоторой условной вероятностью Р(А/Вi), тогда
вероятность наступления события А равна сумме
произведений вероятности каждого события из
полной группы на соответствующую условную
вероятность события А.
Р(А) = Р(В1)Р(А/В1) + Р(В2)Р(А/В2) + … + Р(Вn)Р(А/Вn)
7. Задача 1
На трех станках различной марки изготавливаетсяопределенная деталь. Производительность первого станка за
смену 40 деталей, второго – 35, третьего – 25. Установлено, что
2%,3% и 5% продукции этих станков соответственно имеют
скрытые дефекты. В конце смены взята одна деталь.
Какова вероятность, что она имеет дефект?
А – деталь имеет дефект;
В1 – деталь изготовлена на первом станке;
В2 – деталь изготовлена на втором станке;
В3 – деталь изготовлена на третьем станке.
8.
Р(А) = Р(В1)Р(А/В1) + Р(В2)Р(А/В2) + Р(В3)Р(А/В3)Р(В1)=
Р(А/В1) =
Р(В2)=
Р(А/В2) =
Р(В3) =
Р(А/В3) =
Р(А) =
9. Задача 2.
Была проведена контрольная работав трех группах. В первой группе, где
30 студентов, оказалось 8 работ,
выполненных на «5», во торой, где 25
студентов – 6 работ на «5», в третьей,
где 27 студентов – 9 работ на «5».
Найти вероятность того, что взятая
случайно работа выполнена на «5».
10. Задача 3.
На склад поступили детали с трех станков. На первомизготовлено 40% всех деталей, на втором – 35%, на третьем
– 25%. Причем на первом 90% деталей 1-го сорта, на
втором – 80%, на третьем – 70%. Какова вероятность, что
взятая наугад деталь не 1-го сорта?
11.
2 урокФОРМУЛА БАЙЕСА
12.
Цели обучения10.3.2.6 знать формулу Байеса и применять ее при
решении задач;
13.
Цель урокарассмотреть применение формулы полной
вероятности и формулы Байеса при решении
задач.
14. При выводе формулы полной вероятности предполагается, что событие А, вероятность которого следовало найти, произойдет с одним
изсобытий Вi, образующих полную группу, причем
вероятности событий Вi были известны.
Пусть событие А уже наступило.
Как изменятся при этом условии
вероятности событий Вi ?
15.
Формула БайесаТак как событие А и Вi совместны, то по
теореме умножения:
Р( А Вi ) Р( А) Р( Вi / А) Р( Вi ) Р( A / Bi ) ,
Р( Вi ) Р ( A / Bi )
отсюда Р ( Вi / А)
Р( A)
16. Задача 4
Электронный прибор содержит две микросхемы.Вероятность выхода из строя первой в течении
достаточно длительного времени – 0,2, второй – 0,1.
Известно, что прибор вышел из строя.
Какова вероятность, что вышла из строя 1-я
микросхема?
А – из строя вышел прибор;
В1 – не вышли из строя обе микросхемы;
В2 – отказала первая;
В3 – отказала вторая;
В4 – отказали обе.
17.
Задача 4.Р(В1)=0,8*0,9=0,72
Р(В2)=0,2*0,9=0,18
Р(В3)=0,8*0,1=0,08
Р(В4)=0,2*0,1=0,02
Р(А/В1)=0
Р(А/В2)=1
Р(А/В3)=1
Р(А/В4)=1
18.
Задача 5В первом ящике 8 белых и 6 черных шаров, а во
втором – 10 белых и 4 черных. Наугад выбирают
ящик и шар. Известно, что вынутый шар – черный.
Какова вероятность, что он взят из первого ящика?
19.
Задача 6В урну, содержащую3 шара, положили белый шар,
после чего вынули один. Какова вероятность, что
вынутый шар окажется белым, если все
возможные предположения о цвете уже
имеющихся шаров равновозможны?
20. Решение задач
Приложение 221.
Подведем итоги- что узнал, чему научился?
- что осталось непонятным?
- над чем необходимо работать?







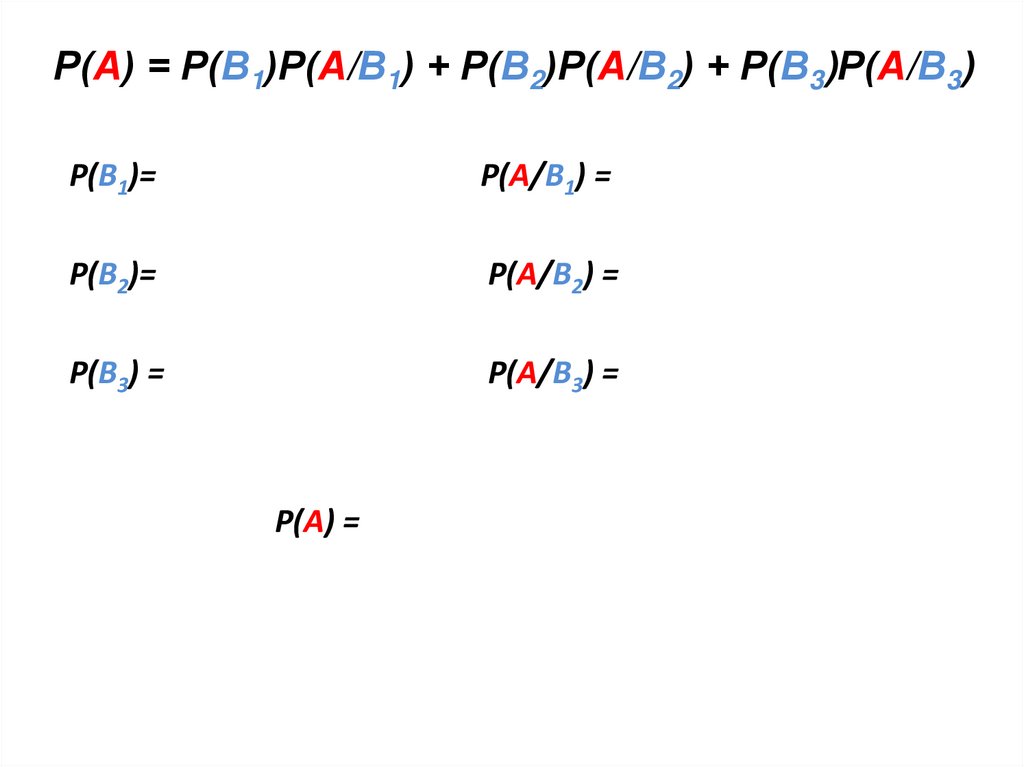













 mathematics
mathematics








