лекция 1

1.

12.12.2025
ОСНОВЫ
МЕХАНИКИ
Гайсина Гузель Абдрахимовна
доцент кафедры Теплоэнергетики и
физики

2.

ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ ПРИ
ВЫПОЛНЕНИИ
ЛАБОРАТОРНЫХ РАБОТ

3.

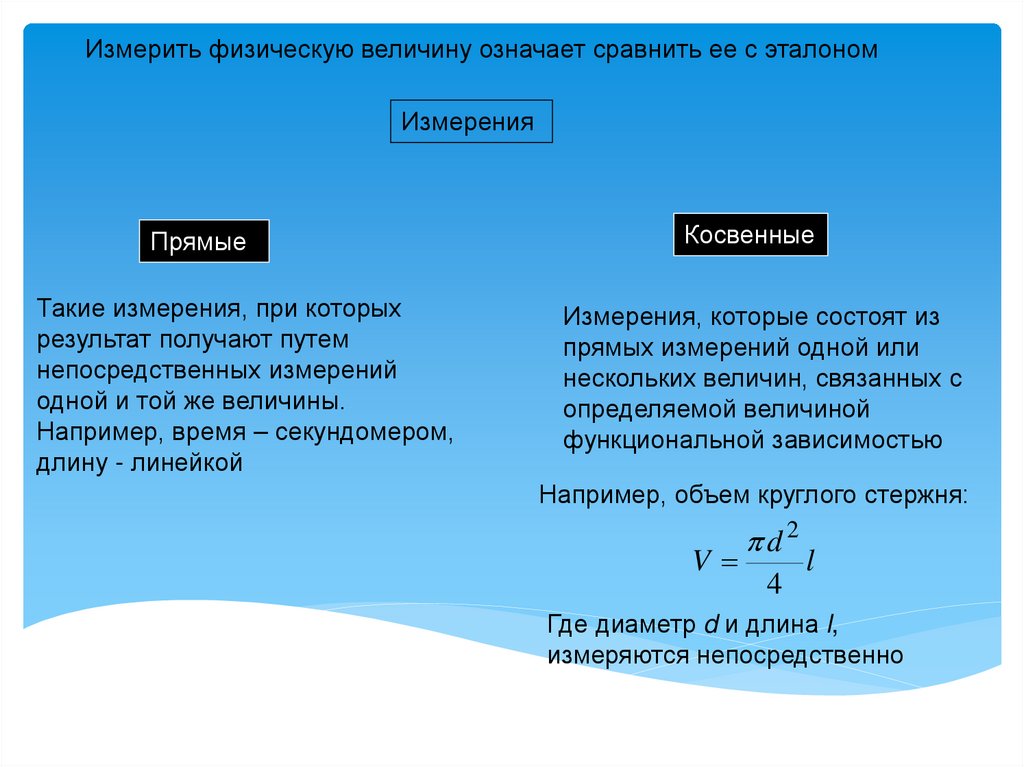
Измерить физическую величину означает сравнить ее с эталоном
Измерения
Прямые
Такие измерения, при которых
результат получают путем
непосредственных измерений
одной и той же величины.
Например, время – секундомером,
длину - линейкой
Косвенные
Измерения, которые состоят из
прямых измерений одной или
нескольких величин, связанных с
определяемой величиной
функциональной зависимостью
Например, объем круглого стержня:
V
d2
4
l
Где диаметр d и длина l,
измеряются непосредственно

4.

Измерения всегда сопровождаются ошибками.
1. Грубые ошибки (промахи)
Например, небрежность, неразборчивость записи, нарушение
условий опыта
В работах грубые ошибки недопустимы. Их следует избегать.
2. Систематические ошибки.
Ошибки, которые сохраняют величину и знак от опыта к опыту.
Являются результатом влияния неучтенных факторов, связанных с
условиями наблюдения (например, не учет каких-либо сил или помех)
или с недостатками измерительных устройств (любой прибор имеет
ограниченную точность)
Систематические ошибки в значительной мере могут быть
обнаружены и устранены как при обработке измерений, так и при
организации измерительного процесса

5.

3. Случайные ошибки.
Ошибки, изменяющие свою величину и знак от опыта к опыту при
измерениях, выполняемых одинаковым образом. Определяются большим
числом случайных причин, действующих в каждом опыте неизвестным
образом.
Исключить случайные ошибки невозможно, но они подчиняются
статистическим закономерностям, поэтому их можно учесть.
Поскольку из-за наличия случайных погрешностей результаты измерений по
своей природе представляют собой тоже случайные величины, истинного
значения xист измеряемой величины получить нельзя.
Однако, ее можно приближенно оценить.
За лучшую оценку истинного значения результата измерений принимают
среднее арифметическое значение
Пусть проведено n измерений величины x. Тогда, среднее арифметическое:
1
~
x
n
n
xi
i 1
xi – результат i-го измерения

6.

Можно установить некоторый интервал значений измеряемой величины
x , в котором с
вблизи полученного в результате измерений значения ~
определенной вероятностью содержится xист. Тогда результат измерений
можно представить в следующем виде:
~
x x xист ~
x x
(1)
xист ~
x x
или
x - погрешность измерений
Вероятность, с которой истиной значение измеренной величины заключено в
интервале (1), называется доверительной вероятностью .
А сам интервал называется доверительным интервалом
Для оценки случайной погрешности измерения наиболее распространена
оценка с помощью стандартного или среднеквадратичного отклонения ~ x
n
~x
i 1
(~
x xi )
n (n 1)
2
xi – результат i-го измерения
n – число измерений

7.

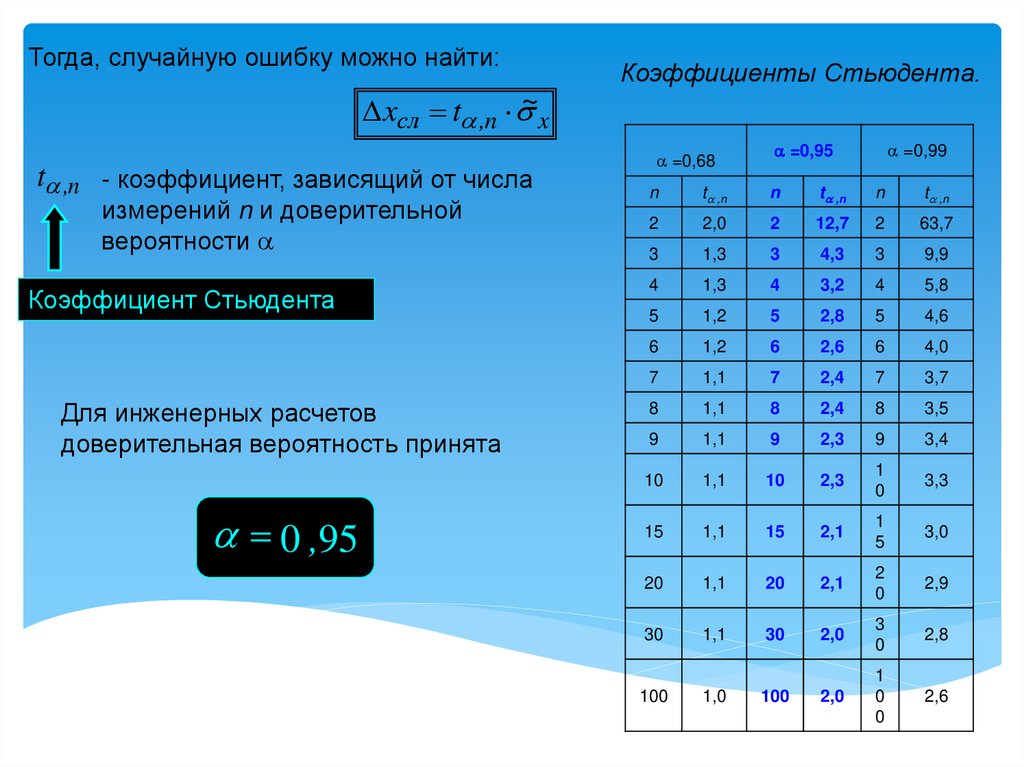
Тогда, случайную ошибку можно найти:
Коэффициенты Стьюдента.
xсл t ,n ~x
t ,n - коэффициент, зависящий от числа
измерений n и доверительной
вероятности
Коэффициент Стьюдента
Для инженерных расчетов
доверительная вероятность принята
0 ,95
=0,68
=0,95
=0,99
n
t ,n
n
t ,n
n
t ,n
2
2,0
2
12,7
2
63,7
3
1,3
3
4,3
3
9,9
4
1,3
4
3,2
4
5,8
5
1,2
5
2,8
5
4,6
6
1,2
6
2,6
6
4,0
7
1,1
7
2,4
7
3,7
8
1,1
8
2,4
8
3,5
9
1,1
9
2,3
9
3,4
10
1,1
10
2,3
1
0
3,3
15
1,1
15
2,1
1
5
3,0
20
1,1
20
2,1
2
0
2,9
30
1,1
30
2,0
3
0
2,8
2,0
1
0
0
2,6
100
1,0
100

8.

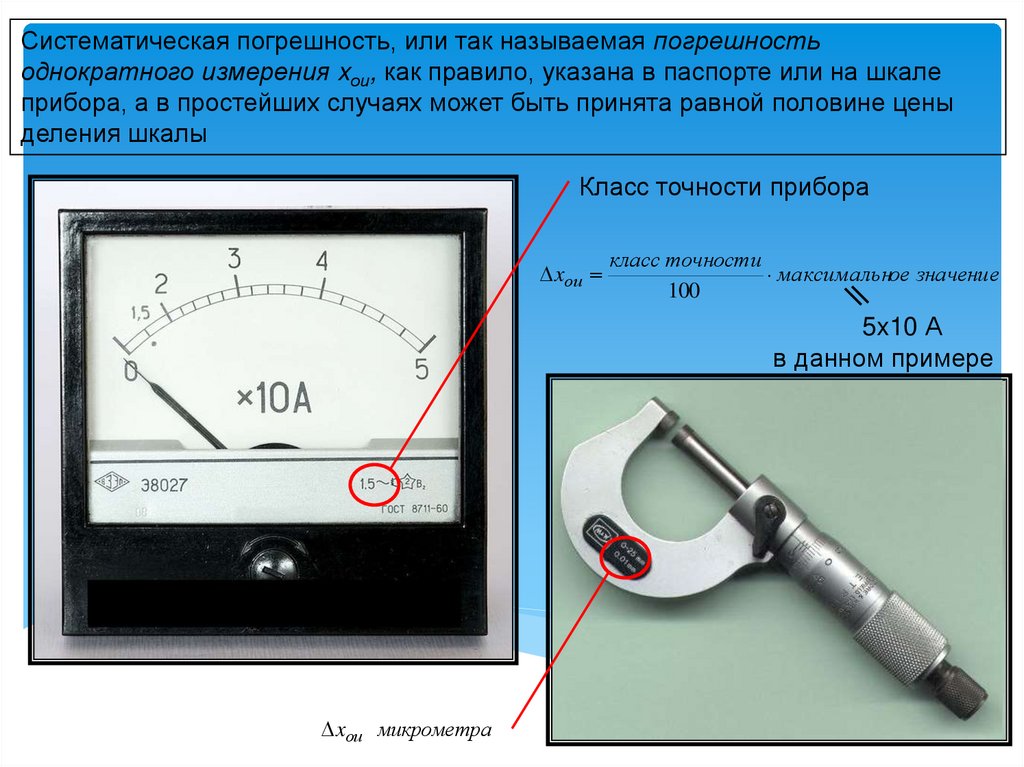
Систематическая погрешность, или так называемая погрешность
однократного измерения xои, как правило, указана в паспорте или на шкале
прибора, а в простейших случаях может быть принята равной половине цены
деления шкалы
Класс точности прибора
xои
класс точности
максимальное значение
100
5x10 А
в данном примере
xои микрометра

9.

Для цифрового прибора точность указывается в паспорте прибора.
При отсутствии паспорта погрешность можно взять по последней
меняющейся цифре соответствующего диапазона измерений.
Точность: 0,001 В

10.

Обычно полная погрешность определяется как корень квадратный из суммы
квадратов случайной ошибки и ошибки однократных измерений:
x
2
2
xсл
xои
x называется абсолютной погрешностью измерений
Очевидно, что при одном и том же значении x результат может оказаться
достаточно точным при измерении некоторой большой величины, тогда как
при измерении малой величины его точность будет недостаточной.
Например, померить
микрометром диаметр болта
Или толщину листа бумаги

11.

Таким образом, необходимо ввести относительную погрешность измерений,
которая определяется как отношение абсолютной погрешности к самой
измеряемой величине:
x
x
~ 100 %
Класс точности прибора - это выраженная в процентах относительная
погрешность, которую дает данный прибор при измерении им наибольшего
значения измеряемой величины, указанной на шкале прибора.

12.

Погрешность косвенно измеряемой величины.
Пусть y - косвенно измеряемая величина, которая является функцией
некоторого числа N величин, измеряемых непосредственно
y f ( x1 , x2 ,...x N )
Относительная погрешность для косвенно измеряемой величины y
определяется
y
~
y
N
2
ln y
xi2
xi
i 1
xi - абсолютная погрешность i-ой величины, измеряемой непосредственно
Абсолютная погрешность для косвенно измеряемой величины:
y ~
y

13.

Рассмотрим вычисление погрешности косвенно определяемой
величины на примере объема параллелепипеда
V a b c
Здесь:
a x1 ; b x2 ; c x3 ;
Тогда:
ln V ln( a b c) ln a ln b ln c
lnV lnV
ln a ln b ln c
(ln a ln b ln c)
x1
a
a
a
a
a
1
(ln a) a (ln b) a (ln c) a 0 0
a
ln V ln V
1
(ln a ln b ln c) 0 0
x2
b
b
b

14.

lnV lnV
1
(ln a ln b ln c) 0 0
x3
c
c
c
Поскольку
~ ~ ~ ~
V a b c
То относительная погрешность измерения объема параллелепипеда:
V
~
V
2
2
2
1
2 1
2 1
2
a
b
c
~
~
~
a
b
c

15.

При обработке результатов измерений рекомендован следующий порядок
операций:
Сначала находят погрешность прямых измерений
1. Вычисляют среднее из n измерений:
1
~
x
n
n
xi
i 1
2. Определяют среднеквадратичное отклонение среднего арифметического:
n
~x
(~
x xi ) 2
i 1
n (n 1)
3. По доверительной вероятности =0,95 и числу измерений n из таблицы
определяют коэффициент Стьюдента t ,n
4. Определяют случайную погрешность:
xсл t ,n ~x

16.

5. Определяют погрешность однократного измерения xои
6. Определяют погрешность абсолютную ошибку прямого измерения x
x
2
2
xсл
xои
7. Если в искомую величину входят несколько величин, которые измеряются
непосредственно, то пункты 1-6 повторяют для каждой из них
Далее находят погрешность косвенных измерений.
8. Устанавливается формула для расчета относительно погрешности
косвенных измерений из общей формулы :
y
~
y
N
2
ln y
xi2
xi
i 1

17.

9. Находят абсолютную погрешность косвенных измерений:
y ~
y
10. Округлить полученный результат.
11. Окончательный результат записывают в виде:
y ~
y y
с =0,95
~
V V V
с =0,95
На примере объема:
Что означает: истинное значение объема с вероятностью 95% лежит в
~
~
интервале от V V до V V

18.

Округление результата
Пусть, например, в работе М-00 получен следующий результат для объема тела:
V 5678 ,5468 64,2345 мм
3
Округление начинают с погрешности. Значащей цифрой является самая
левая, если она не единица.
Итак, самой левой в 64 ,2345
округляем до десятков
является шестерка, следовательно,
64 ,2345 60
Значит, до десятков следует округлить и сам результат:
5678 ,5468 5680
Окончательно:
V 5680 60 мм3
c 0,95

19.

В случае, если левой цифрой в погрешности является единица, то
значащей будет следующая за ней, и до нее же округляется
результат. Например:
V 5678 ,5468 14,2345 мм
3
Тогда ответ:
V 5678 14 мм3 c 0,95

20. Тема 1. КИНЕМАТИКА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

1.1. Понятие механики, модели в механике
1.2. Система отсчета, тело отсчета
1.3. Кинематика материальной точки
1.3.1. Путь, перемещение
1.3.2. Скорость
1.3.3. Проекция вектора скорости на оси
координат
1.3.4.
Ускорение.
Нормальное
и
тангенциальное ускорение
1.4. Кинематика твердого тела
1.4.1. Поступательное движение твердого тела
1.4.2.
Вращательное
движение
вокруг
неподвижной оси
20

21.

1.1. Понятие механики, модели в механике
Механика – раздел физики, в котором
изучаются закономерности механического
движения и причины, вызывающие или
изменяющие это движение.
Механическое движение – это изменение
с течением времени взаимного расположения
тел или их частей.
Механика подразделяется на три части:
статику, кинематику и динамику.
21

22.

Кинематика (от греческого слова kinema –
движение) – раздел механики, в котором изучаются
геометрические свойства движения тел без учета
их массы и действующих на них сил.
Динамика (от греческого dynamis – сила) изучает
движения тел в связи с теми причинами, которые
обуславливают это движение.
22

23.

Статика (от греческого statike – равновесие)
изучает условия равновесия тел.
Поскольку равновесие – есть частный случай
движения, законы статики являются естественным
следствием законов динамики и в данном курсе не
изучается.
Без знаний механики невозможно представить
себе развитие современного машиностроения.
Развитие механики, как науки, начиналось с III в. до
н.э., когда древнегреческий ученый Архимед (287 – 312
до
н.э.)
сформулировал
равновесия плавающих тел.
закон
23
рычага
и
законы

24.

Основные
законы
механики
установлены
итальянским физиком и астрономом Г. Галилеем
(1564 – 1642) и окончательно сформулированы
английским физиком И. Ньютоном (1643 – 1727).
Механика
Галилея
и
Ньютона
называется
классической, т.к. она рассматривает движение
макроскопических тел со скоростями, значительно
меньшими скорости света в вакууме.
24

25.

Галилео Галилей
(Galileo Galilei)
Родился
15 февраля 1564
Пиза (Pisa)
Италия
Умер
8 января 1642
Арчетри (Arcetri)
Италия
астроном, философ и физик.
Важнейшие роботы
улучшение телескопа;
астрономические
наблюдения;
первый закон движения
25

26.

Исаак Ньютон
(Isaac Newton)
Родился
4 января 1643
Вулсторп (Woolsthorpe)
Англия
Умер
31 марта 1727
Лондон (London)
Англия
физик, математик, астроном,
алхимик и философ
Важнейшие работы
закон всемирного тяготения
дифференциальное и
интегральное исчисления
изобрел зеркальный телескоп
развил корпускулярную теорию
26
света

27.

Альберт Эйнштейн
(Albert Einstein)
Родился
14 марта 1879
Ульм (Ulm)
Германия
Умер
18 апреля 1955
Принцетон (Princeton )
США (New Jersey)
величайший ученый 20 века
Важнейшие работы:
теория относительности;
квантовая и статистическая
механика; космология
Нобелевская премия по
физике 1921
27

28.

Для описания движения тел в зависимости от
условий задачи используют различные физические
модели. Наиболее часто используемые понятия:
абсолютно твердое тело и материальная точка.
Движение тел происходит под действием сил. Под
действием
внешних
сил
тела
могут
деформироваться, т.е. изменять свои размеры и
форму.
Абсолютно твердое тело - тело, деформацией
которого в условиях данной задачи можно
пренебречь (хотя абсолютно твердых тел в природе
не существует).
28

29.

Материальная точка - тело, размерами которого
в условиях данной задачи, можно пренебречь.
Можно ли данное тело рассматривать как
материальную точку или нет, зависит не от размеров
тела, а от условия задачи (например, наше огромное
Солнце – тоже материальная точка в Солнечной
системе).
29

30.

1.2. Система отсчета, тело отсчета
Всякое движение относительно, поэтому
для
описания
движения
необходимо
условиться, относительно какого другого тела
будет отсчитываться перемещение данного
тела. Выбранное для этой цели тело называют
телом отсчета.
Практически, для описания движения
приходится связывать с телом отсчета систему
координат (декартова, сферическая, полярная
и т.д.).
30

31.

Система отсчета – совокупность
системы координат и часов, связанных с телом
по отношению к которому изучается движение.
Движения тела, как и материи, вообще не
может быть вне времени и пространства.
Материя, пространство и время неразрывно
связаны между собой (нет пространства без
материи и времени и наоборот).
31

32.

Пространство
трехмерно,
поэтому
«естественной» системой координат является,
декартова
или
прямоугольная
система
координат, которой мы в основном и будем
пользоваться.
В
декартовой
системе
координат,
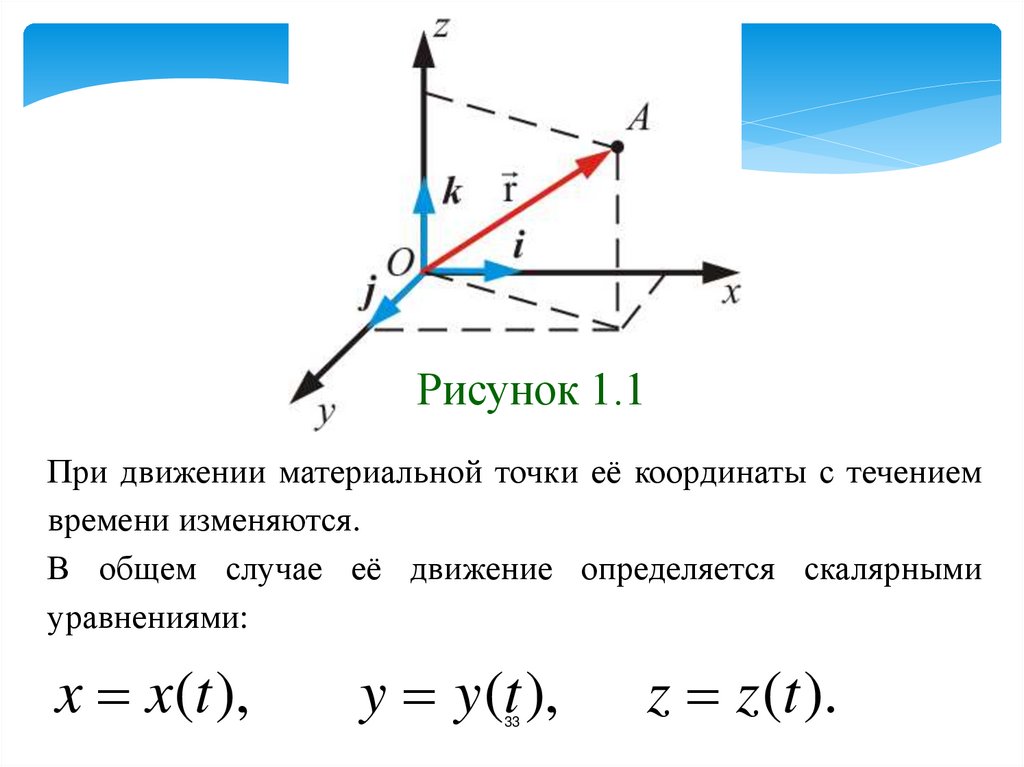
положение точки А в данный момент времени
по отношению к этой системе характеризуется
тремя координатами x, y, z или радиус-вектором
, проведенным из начала координат в данную
точку (рисунок 1.1).
32

33.

Рисунок 1.1
При движении материальной точки её координаты с течением
времени изменяются.
В общем случае её движение определяется скалярными
уравнениями:
x x(t ),
y y (t ),
33
z z (t ).

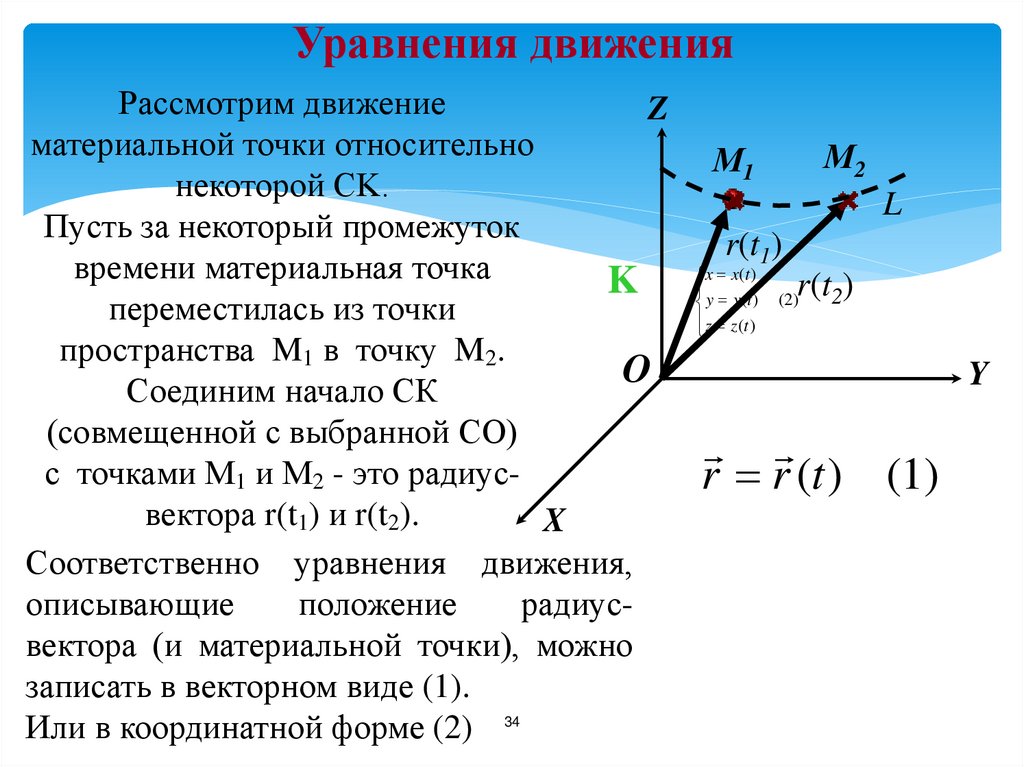
34. Уравнения движения

Рассмотрим движение
Z
материальной точки относительно
некоторой СK.
Пусть за некоторый промежуток
времени материальная точка
K
переместилась из точки
пространства M1 в точку M2.
O
Соединим начало СК
(совмещенной с выбранной СО)
с точками M1 и M2 - это радиусвектора r(t1) и r(t2).
X
Соответственно уравнения движения,
описывающие
положение
радиусвектора (и материальной точки), можно
записать в векторном виде (1).
Или в координатной форме (2) 34
М2
М1
L
r(t1)
x x(t )
y y (t )
z z (t )
r(t2)
(2)
Y
r r (t ) (1)

35.

Эти уравнения эквивалентны векторному уравнению
r r t xi yj zk
(3)
где
х, у,
z – проекции радиус-вектора r на оси координат,
i , j , k – единичные векторы (орты), направленные
по соответствующим осям.
Уравнения (2) и (3) называются кинематическими
уравнениями движения материальной точки.
35

36.

Число независимых координат, полностью
определяющих положение точки в пространстве,
называется числом степеней свободы.
Если
материальная
точка
движется
в
пространстве, то она имеет три степени свободы
(координаты х, у, z). Если она движется на плоскости
– две степени свободы. Если вдоль линии – одна
степень свободы.
36

37.

Всякое движение тела можно разложить на два
основных вида движения – поступательное и
вращательное.
Поступательное – это такое движение, при
котором любая прямая связанная с движущимся
телом остается параллельной самой себе и все точки
твердого тела совершают равные перемещения за
одинаковое время
Рисунок 1.2
37

38.

При вращательном движении все точки тела
движутся по окружностям, центры которых лежат на
одной и той же прямой ОО , называемой осью
вращения (рисунок 1.3).
Из определения вращательного движения ясно, что
понятие вращательного движения для материальной точки
неприемлемо.
Рисунок 1.3
38

39.

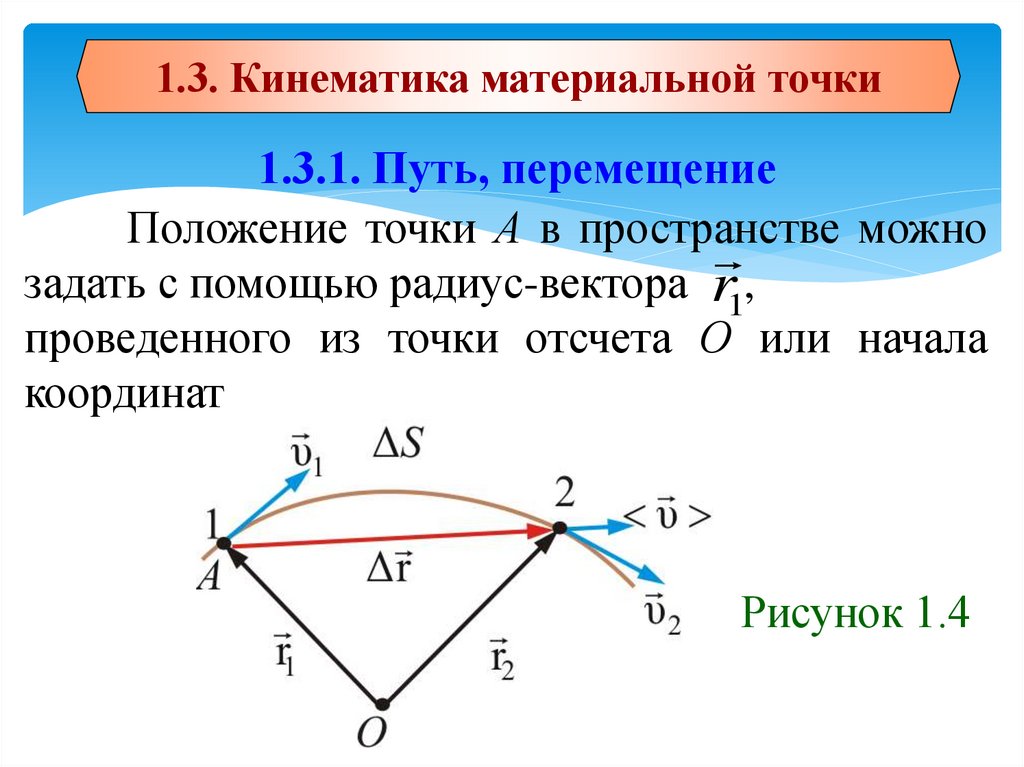
1.3. Кинематика материальной точки
1.3.1. Путь, перемещение
Положение точки А в пространстве можно
задать с помощью радиус-вектора r1,
проведенного из точки отсчета О или начала
координат
Рисунок 1.4
39

40.

При движении точки А из точки 1 в точку 2 её
радиус-вектор изменяется и по величине, и по
направлению, т.е. r зависит от времени t.
Геометрическое
место
точек, которые
описывает конец радиус-вектора, называется
траекторией точки.
Длина траектории есть путь ΔS. Если точка
движется по прямой, то приращение r равно пути
S.
40

41.

Пусть за время t точка А переместилась из
точки 1 в точку 2.
Вектор перемещения r есть приращение r1 за
время t
Δr r2 r1 x x0 i y y0 j z z0 k
Δr Δxi Δyj Δzk
2
2
2
Δr Δx Δy Δz .
41

42. 1.3.2. Скорость

Средний
вектор
скорости
определяется как отношение вектора
перемещения r ко времени t, за
которое это перемещение произошло
Δr
υ
Δt
Вектор Δ r
совпадает с
направлением
вектора υ
42

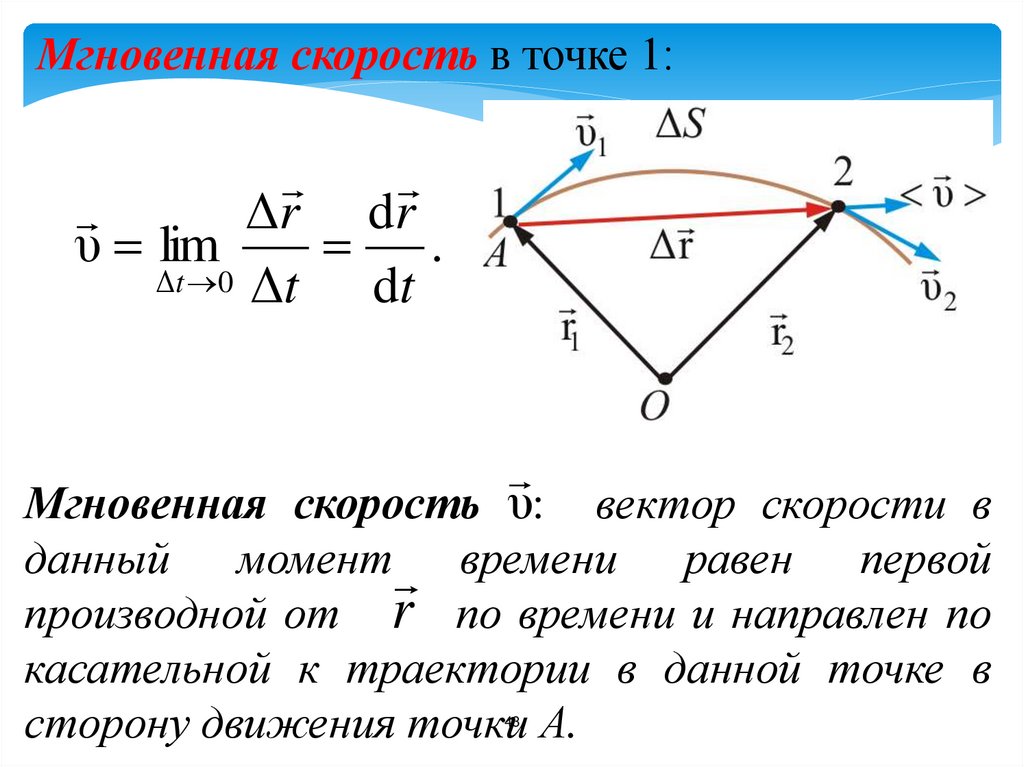
43.

Мгновенная скорость в точке 1:
Δr d r
υ lim
.
Δt 0 Δt
dt
Мгновенная скорость υ:
вектор скорости в
данный момент времени равен первой
производной от r по времени и направлен по
касательной к траектории в данной точке в
сторону движения точки А.
43

44.

Модуль вектора скорости
dr
υ υ
.
dt
При t 0 т.е. на бесконечно малом участке
траектории S = r (перемещение совпадает с
траекторией).
В этом случае мгновенную скорость можно
выразить через скалярную величину – путь
ΔS dS
υ lim
;
Δt
dt
Δt 0
dS
или υ
.
dt
Так вычислять скорость проще, т.к. S – скаляр
44

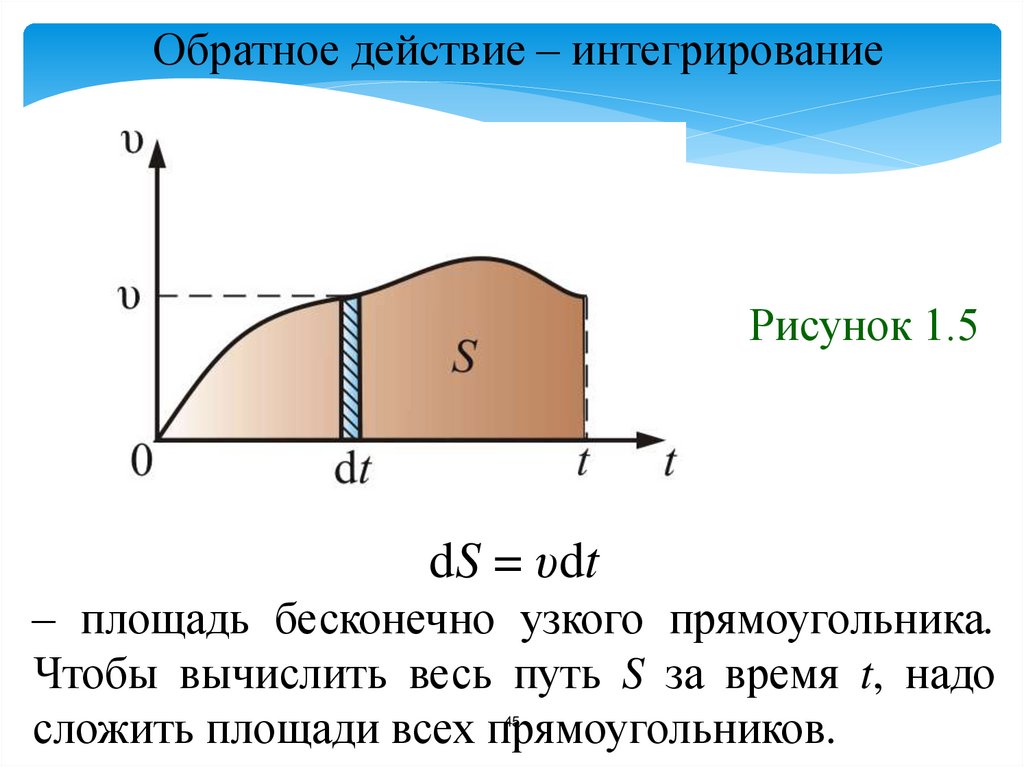
45.

Обратное действие – интегрирование
Рисунок 1.5
dS = υdt
– площадь бесконечно узкого прямоугольника.
Чтобы вычислить весь путь S за время t, надо
сложить площади всех прямоугольников.
45

46.

t
S υdt.
0
Геометрический смысл этого интеграла в том,
что площадь под кривой υ(t) есть путь тела
за время t.
46

47.

В физике существует общий принцип, который
называется принцип суперпозиций (принцип
наложения) – допущение, согласно которому
результирующий эффект сложного процесса
взаимодействия
представляет
собой
сумму
эффектов, вызываемых каждым воздействием в
отдельности, при условии, что последние взаимно не
влияют друг на друга.
Принцип суперпозиции играет большую роль
во многих разделах физики и техники.
47

48. 1.3.3. Проекция вектора скорости на оси координат

В векторной форме уравнения записываются легко и
кратко. Но для практических вычислений нужно знать
проекции вектора на оси координат выбранной системы
отсчета.
Положение точки А
(рисунок 1.5) задается
радиус-вектором r .
Спроецируем вектор r
на оси – x, y, z.
Рисунок 1.5
48

49.

Понятно, что х, y, z зависят от времени t, т.е. x(t),
y(t), z(t). Зная зависимость этих координат от времени
(закон движения точки) можно найти в каждый
момент времени скорость точки.
Проекция вектора скорости на ось x равна:
dx
x
dt
Здесь dx – проекция вектора перемещения dr на ось х.
Аналогично:
dy
dz
y ; z .
dt
dt
49

50.

Модуль вектора скорости
2
2
2
х у z
Так как вектор, то
dx dy dz
υ υ xi υ y j υ z k i
j k
dt
dt
dt
где: i , j , k - единичные векторы – орты.
50

51. 1.3.4. Ускорение. Нормальное и тангенциальное ускорения

В произвольном случае движения скорость не
остается постоянной. Быстрота изменения скорости
по времени и направлению характеризуются
ускорением:
d
a
dt
Ускорение величина векторная.
При криволинейном движении изменяется также и по
направлению.
51

52.

(рисунок 1.6),
τ
Введем единичный вектор
связанный с точкой 1 и направленный по
касательной
к
траектории
движения
точки
1
(векторы и τ в точке 1 совпадают).
Тогда можно записать:
υ = υτ,
Где
скорости.
– модуль вектора
Рисунок 1.6
52

53.

Найдем ускорение
d d
dτ
a
τ a an .
dt dt
dt
Получили два слагаемых ускорения:
aτ – тангенциальное ускорение, совпадающее
с направлением в данной точке.
a n – нормальное ускорение
или центростремительное.
υ
53

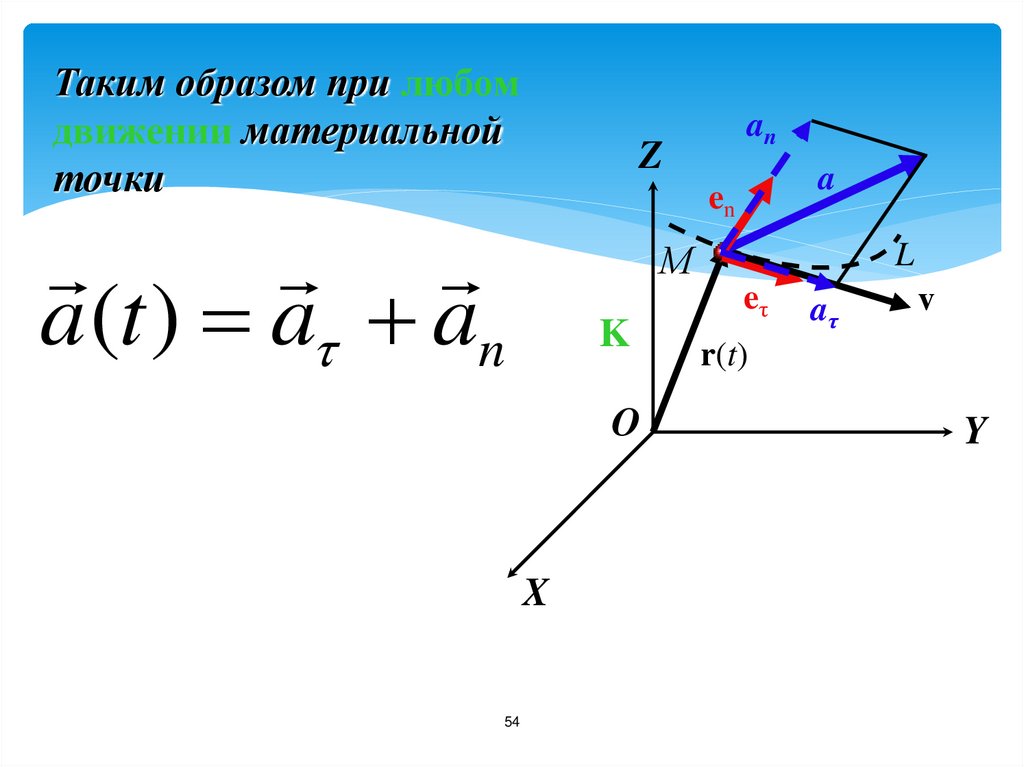
54.

Таким образом при любом
движении материальной
точки
Z
a
en
a (t ) a an
М
K
O
X
54
an
L
eτ
aτ
v
r(t)
Y

55.

dυ
aτ
τ
dt
a τ показывает
величине:
d
0
1)
dt
aτ
ускоренное
движение
или по модулю
изменение
вектора
d
0
2)
dt
aτ
замедленное
движение
55
dυ
aτ
dt
скорости
по
d
0
dt
3)
aτ 0
const
движение с
постоянной по
модулю
скоростью

56.

Рассмотрим подробнее второе слагаемое уравнения
dτ
an .
dt
Быстрота изменения направления касательной
к траектории (dτ/dt ) определяется скоростью
движения точки по окружности и степенью
искривленности траекторий.
Степень
искривленности
плоской
кривой
характеризуется кривизной С.
56

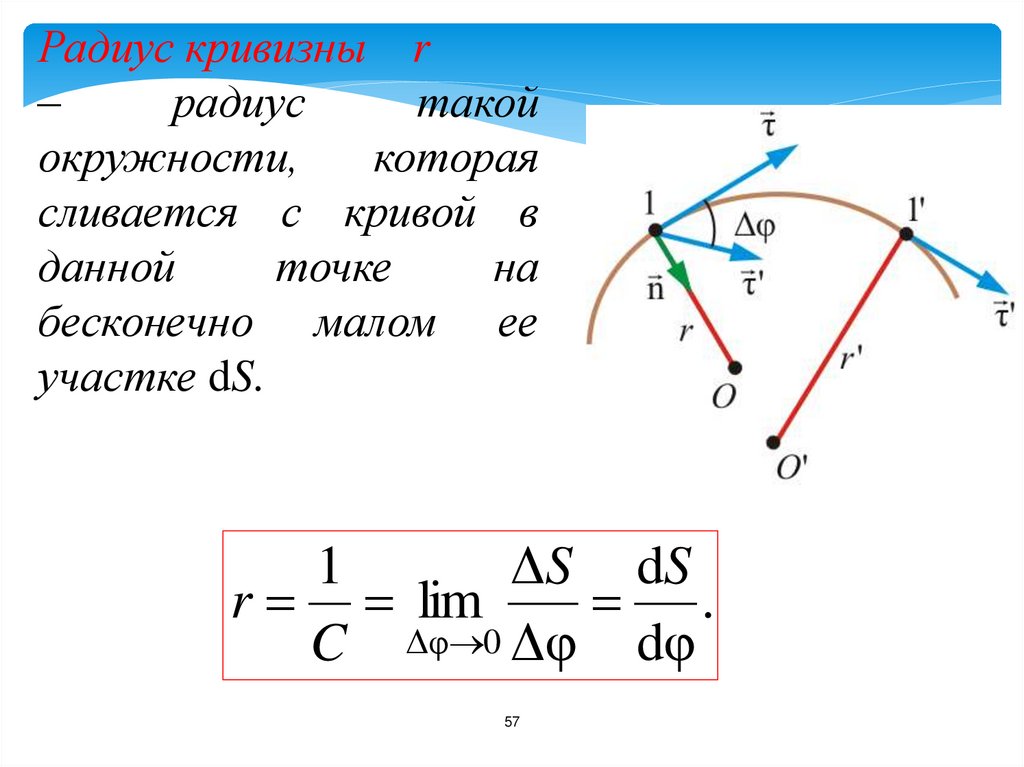
57.

Радиус кривизны r
–
радиус
такой
окружности,
которая
сливается с кривой в
данной
точке
на
бесконечно малом ее
участке dS.
1
ΔS dS
r lim
.
C Δφ 0 Δφ dφ
57

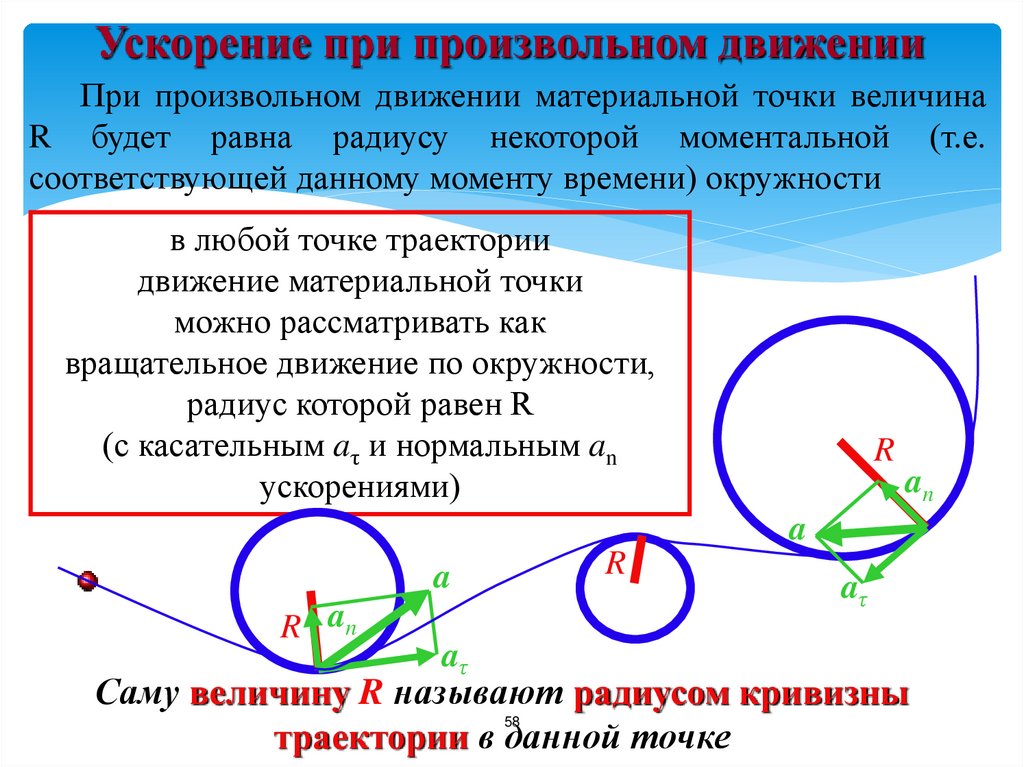
58.

Ускорение при произвольном движении
При произвольном движении материальной точки величина
R будет равна радиусу некоторой моментальной (т.е.
соответствующей данному моменту времени) окружности
в любой точке траектории
движение материальной точки
можно рассматривать как
вращательное движение по окружности,
радиус которой равен R
(с касательным aτ и нормальным an
ускорениями)
R
an
a
R
a
R an
aτ
aτ
Саму величину R называют радиусом кривизны
траектории в данной точке
58

59.

dτ dφ
n
dt dt
Рисунок 1.7
Скорость изменения направления касательной можно
выразить как произведение скорости изменения угла
на единичный вектор n, показывающий направление
изменения угла.
59

60.

Здесь n – единичный вектор, направленный
перпендикулярно касательной (τ) в данной точке,
т.е. по радиусу кривизны к центру кривизны.
dS
dφ
r
dS dt
2
dτ υ
υ n
dt
r
dτ υ
n
dt r
υdt
dφ
.
r
dφ υ
dt r
отсюда
υ
an n ,
r
2
нормальное
ускорение
или
an –
центростремительное, т.к. направлено оно к
центру кривизны, перпендикулярно вектору τ
60

61.

Нормальное ускорение показывает быстроту
изменения направления вектора скорости.
Центростремительное
ускорение
–
это
ускорение при движении происходящем по
окружности.
an an .
r
2
А когда движение происходит по произвольной
кривой
–
говорят:
нормальное
ускорение,
перпендикулярное к касательной в любой точке
траектории.
61

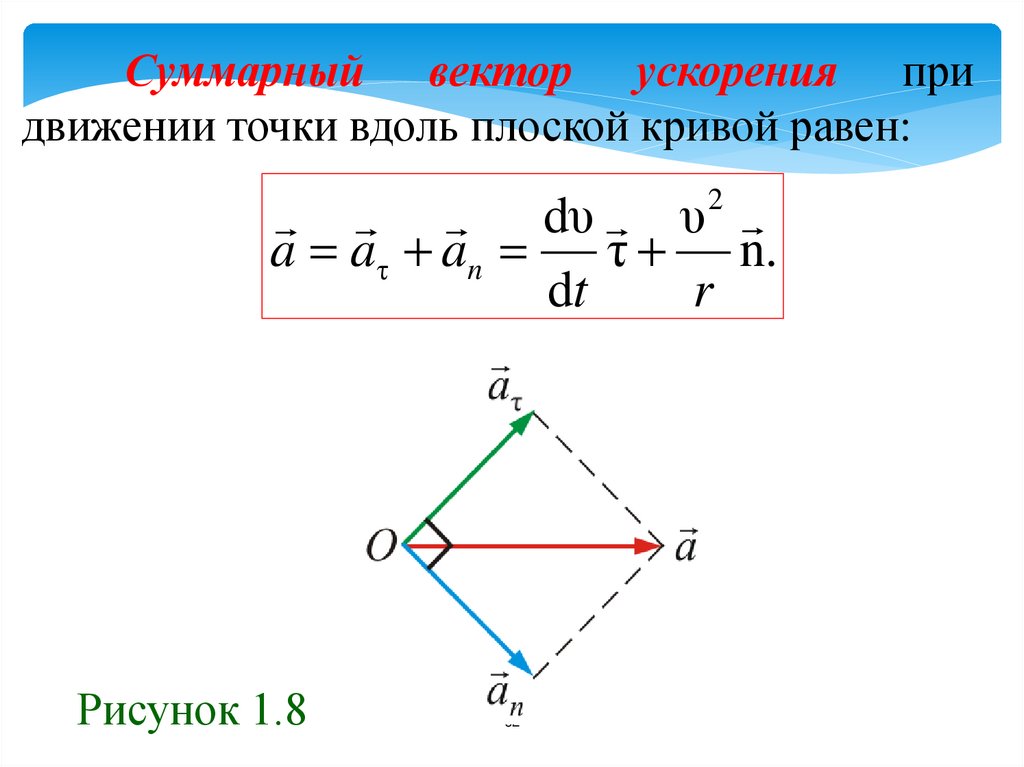
62.

Суммарный вектор ускорения при
движении точки вдоль плоской кривой равен:
dυ υ
a a τ an
τ n.
dt
r
2
Рисунок 1.8
62

63.

Как видно из этого рисунка, модуль общего ускорения
равен:
a a 2 an2
Рассмотрим
несколько
предельных
(частных)
случаев:
а = 0; аn = 0 – равномерное прямолинейное
движение;
а = const; аn = 0 – равноускоренное прямолинейное
движение;
а = 0; аn = const – равномерное движение по
окружности.
.
63

64.

Вспомним несколько полезных формул:
t
При равномерном движении S dt t
0
При движении с постоянным ускорением
t
t
2
at
S atdt a tdt
,
2
0
0
Если
0 at
at 2
S 0t
2
(а = const) то:
S
2а
2
2
0
64
0
S
t.
2

65.

Обратная задача кинематики заключается
в том, что по известному значению ускорения a(t)
найти скорость точки и восстановить траекторию
движения r(t).
d (t )
a(t )
,
По определению
dt
t
2
отсюда
(t ) (t0 ) a(t )dt
или, так как
Следовательно
dr
(t ) ,
dt
t1
t2
r (t ) r (t0 ) (t )dt.
t1
65

66.

1.4. Кинематика твердого тела
Различают пять видов движения твердого тела:
- поступательное;
- вращательное вокруг неподвижной оси;
- плоское;
- вокруг неподвижной точки;
- свободное.
Поступательное движение и вращательное
движение вокруг оси – основные виды движения
твердого тела.
Остальные виды движения твердого тела можно свести
к одному их этих основных видов или к их
совокупности.
66

67. 1.4.1. Поступательное движение твердого тела

Как было отмечено в п. 1.1, поступательное
движение – это такое движение твердого тела, при
котором любая прямая, связанная с телом, остается
параллельной своему начальному положению и при
этом, все точки твердого тела совершают за один и
тот же промежуток времени равные перемещения
(рисунок 1.2). Поэтому скорости и ускорения всех
точек твердого тела в данный момент времени t
одинаковы.
Это
позволяет
свести
изучение
поступательного движения твердого тела к изучению
движения отдельной точки, т.е. к задаче кинематики
материальной точки, подробно рассмотренной в п. 1.3.
67

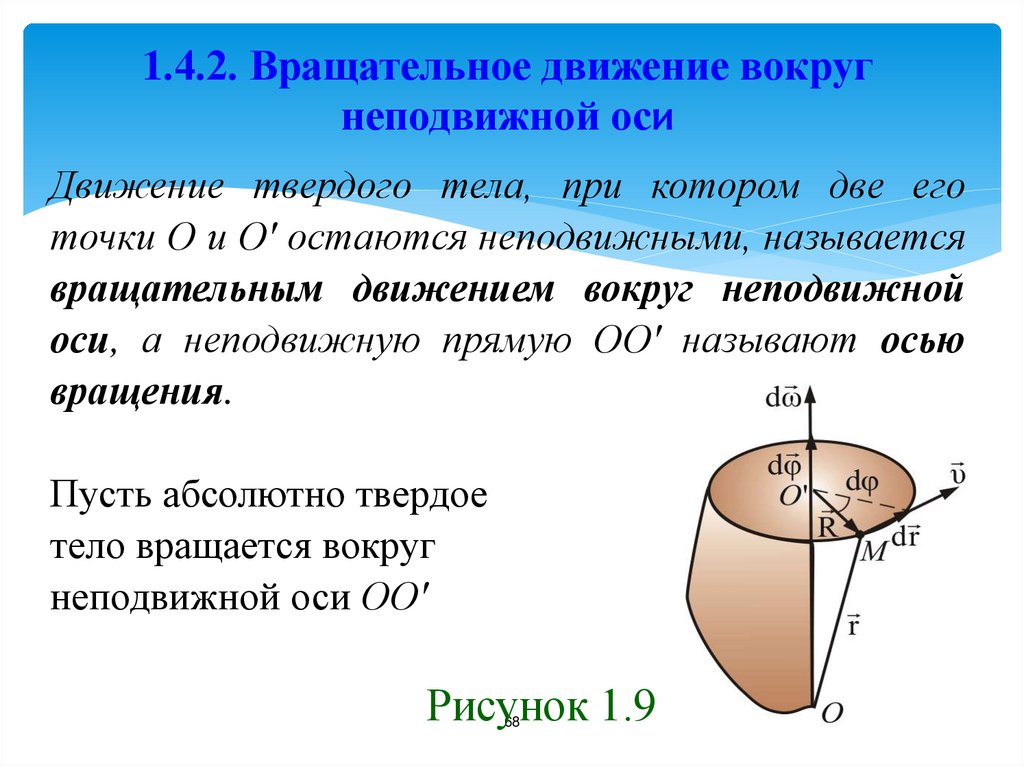
68. 1.4.2. Вращательное движение вокруг неподвижной оси

Движение твердого тела, при котором две его
точки О и О' остаются неподвижными, называется
вращательным движением вокруг неподвижной
оси, а неподвижную прямую ОО' называют осью
вращения.
Пусть абсолютно твердое
тело вращается вокруг
неподвижной оси ОО'
Рисунок 1.9
68

69.

Проследим за некоторой точкой М этого твердого
тела. За время dt точка М совершает элементарное
перемещение
При том же самом угле поворота d другая точка,
отстоящая от оси на большее или меньшее расстояния,
совершает другое перемещение. Следовательно, ни
само перемещение некоторой точки твердого тела, ни
первая производная dr
dt 2
d r
ни вторая производная
dt
2
не могут служить
характеристикой движения
всего твердого тела.
69

70.

Угол поворота d характеризует перемещения всего
тела за время dt.
Удобно ввести dφ – вектор элементарного поворота
тела, численно равный d и направленный вдоль оси
вращения ОО' так, чтобы глядя вдоль вектора dφ
мы видели вращение по
часовой стрелке (направление
вектора dφ и направление
вращения связаны правилом
буравчика).
70

71.

Элементарные повороты удовлетворяют обычному
правилу сложения векторов:
dφ dφ1 dφ 2 .
Угловая скорость ω - вектор
численно
равный первой производной от угла поворота по
времени и направленный вдоль оси вращения в
направлении dφ ( dφ и ω всегда направлены в одну
сторону).
dφ
ω
dt
dφ
ω .
dt
71

72.

Связь линейной и угловой скорости
Пусть – линейная скорость точки М.
За промежуток времени dt точка М проходит путь
В
то
dr dt.
же время
dr Rdφ (центральный угол).
Тогда,
dr Rdφ
υ
ωR
dt
dt
72

73.

[ , R ]
В векторной форме
Вектор ортогонален к векторам ω и R
и направлен в ту
же
сторону,
что
и
векторное
произведение [ , R ]
73

74.

Период Т – промежуток времени, в течение
которого тело совершает полный оборот (т.е.
поворот на угол = 2 ).
2πR 2π
Т
;
ω
Частота ν – число оборотов тела за 1 сек.
Угловая скорость
1
ν .
Т
2π
ω
2πν;
Т
74

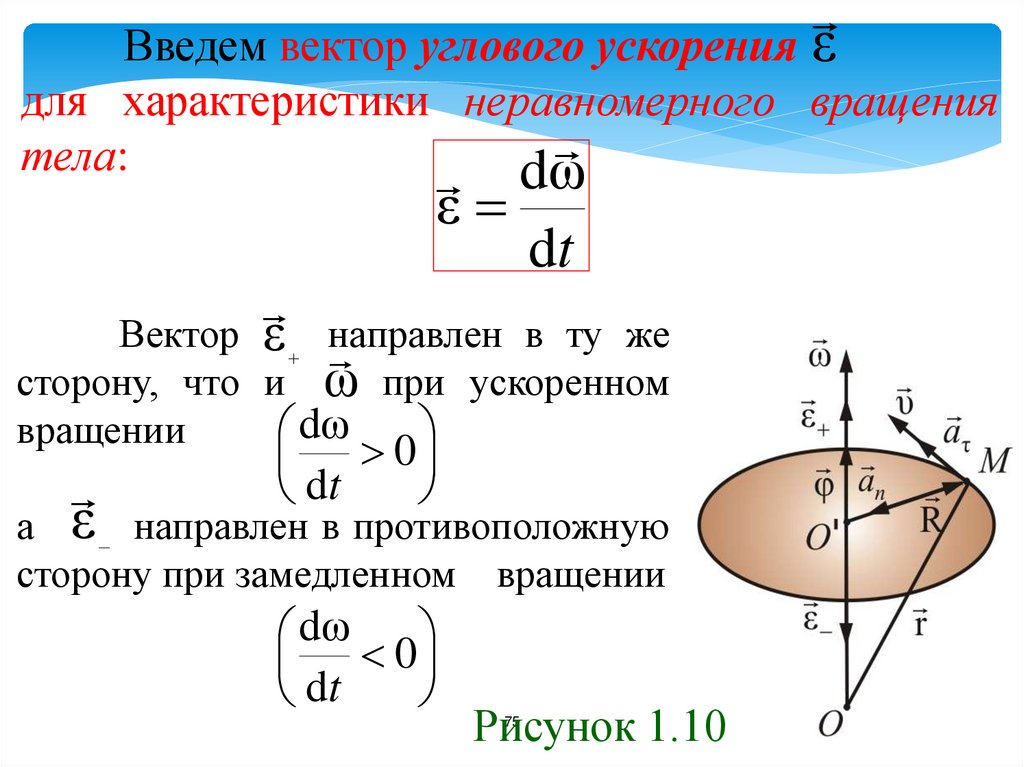
75.

Введем вектор углового ускорения ε
для характеристики неравномерного вращения
тела:
dω
ε
dt
Вектор ε направлен
в ту же
сторону, что и ω при ускоренном
вращении
dω 0
dt
а ε направлен в противоположную
сторону при замедленном
dω 0
dt
вращении
Рисунок 1.10
75

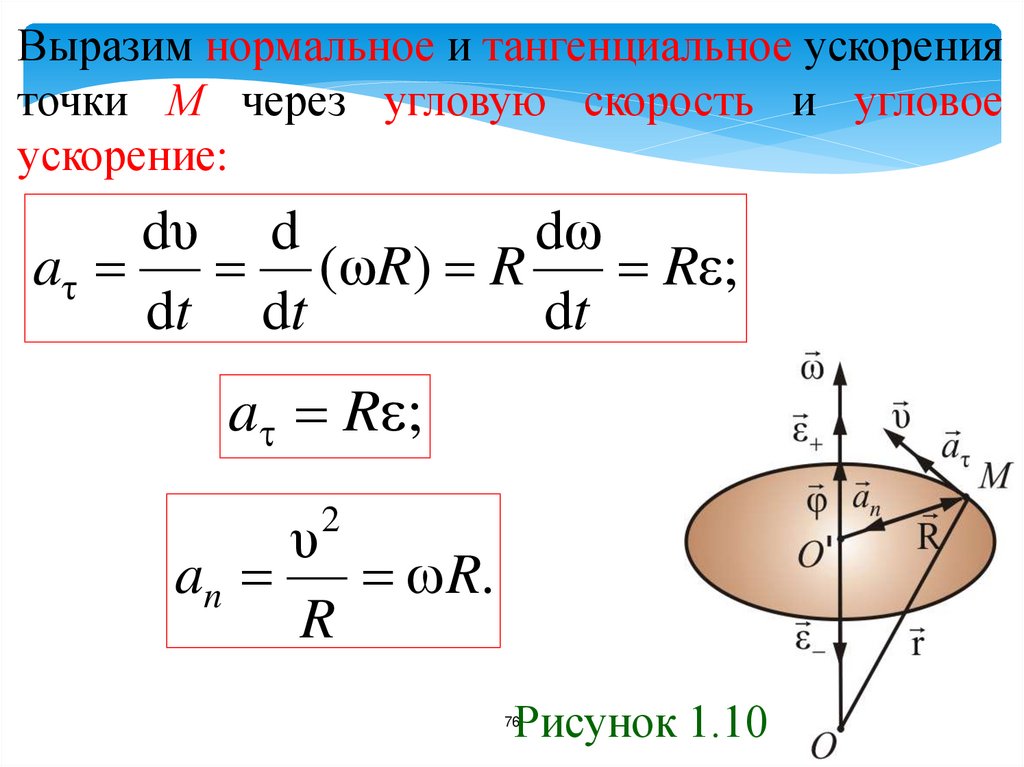
76.

Выразим нормальное и тангенциальное ускорения
точки М через угловую скорость и угловое
ускорение:
dυ d
dω
aτ
(ωR) R
Rε;
dt dt
dt
a R ;
υ
an
R.
R
2
Рисунок 1.10
76

77.

Формулы простейших случаев вращения
тела вокруг неподвижной оси:
- равномерное вращение
ε = 0, ω = const
φ φ0 ωt ;
- равнопеременное
вращение
ω ω 0 εt
εt
φ ω 0t
2
2
77
ε = const

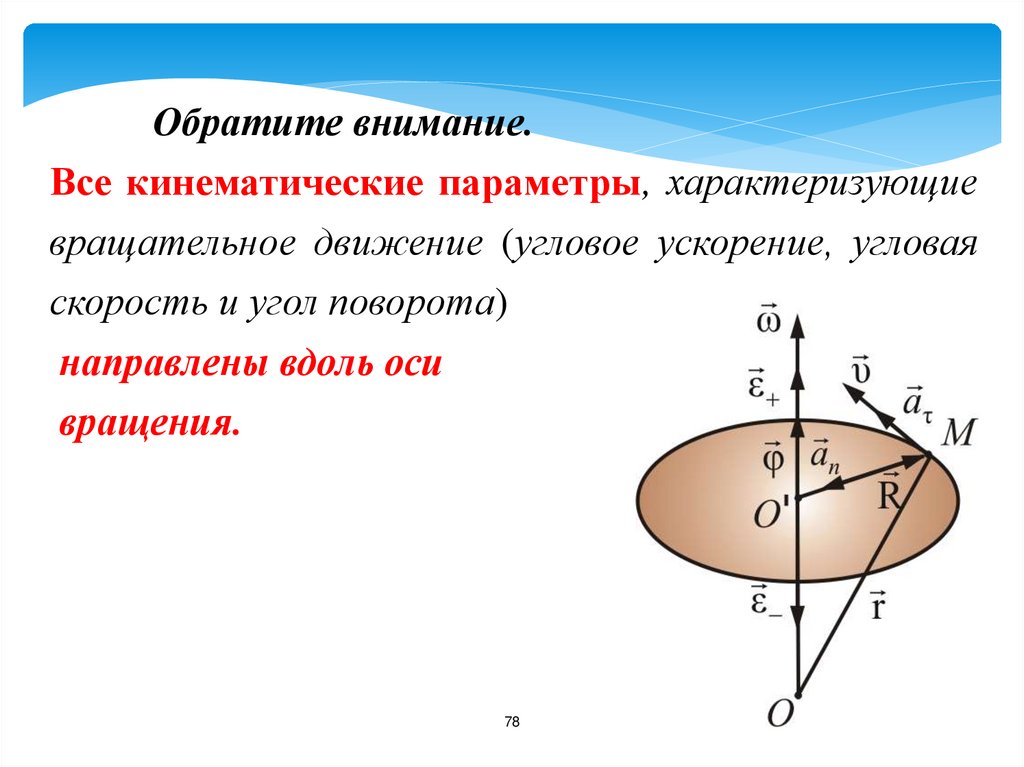
78.

Обратите внимание.
Все кинематические параметры, характеризующие
вращательное движение (угловое ускорение, угловая
скорость и угол поворота)
направлены вдоль оси
вращения.
78