Лекция 1_Введение в математическое моделирование ХТП

1.

Обзор классификации
математических моделей
химико-технологических
процессов
Иерархия моделей: источники данных, структура, типы
уравнений, временные характеристики.

2.

Основы и контекст моделирования
химико-технологических процессов
Моделирование базируется на законах сохранения
массы, энергии и импульса. Важны особенности
уравнений, пространственное распределение и
временная зависимость для точного анализа
процессов.
2

3.

Типы моделей по источнику информации
Детерминированные модели
Стохастические модели
Гибридные модели
Основаны на физических законах с
причинно-следственной связью, всегда
дают одинаковый результат при заданных
условиях. Применяются для кинетики
реакций и материальных балансов.
Учитывают вероятностные факторы,
ошибки измерений, флуктуации и
неопределённости, что повышает
надёжность при моделировании реальных
процессов с шумами.
Совмещают детерминированные и
стохастические подходы, улучшая точность
и адаптивность через комбинирование
физических законов и статистических
методов.
3

4.

Модели с сосредоточенными
параметрами (ODE)
Переменные зависят только от времени, что
упрощает анализ и решение уравнений.
Часто применяются для реакторов с
идеальным перемешиванием, например,
CSTR.
Пример уравнения материального баланса:
V·dС_A/dt = Q·(C_A,in - C_A) - k·C_A·V. В
стационарном режиме концентрация
рассчитывается по формуле C_A = C_A,in / (1 +
k·V/Q). Ограничения связаны с однородностью
системы.
4

5.

Модели с распределёнными
параметрами (PDE)
Переменные зависят от времени и
пространственных координат, позволяя
описывать процессы с профильными
распределениями, например, трубчатые
реакторы или диффузию.
Основное уравнение: ∂x/∂t + u·∂x/∂z = D·∂²x/∂z² + f(x).
Концентрация в реакторе изменяется
экспоненциально: C_A(z) = C_A,in·exp(-k·z/u). PDE
моделирование обеспечивает более высокую
точность при анализе.
5

6.

Фундаментальный материальный
баланс в химических реакторах
Уравнение баланса и конверсия
Общее материальное уравнение: dN/dt = N_in N_out + ν·r·V. Для CSTR с реакцией первого порядка
концентрация C_A = C_A,in / (1 + k·τ).
Зависимость конверсии от параметров
Конверсия выражается формулой X_A = k·τ / (1 + k·τ).
Повышение времени пребывания увеличивает
конверсию, но с убывающей отдачей. Увеличение
скорости реакции значительно повышает
эффективность.
6

7.

Энергетический баланс и контроль
температуры
Компоненты энергетического
баланса
Уравнение баланса включает участие
конвекции, тепловыделения реакции и
теплоотдачи через рубашку: ρ·c_p·V·dT/dt =
Q·ρ·c_p·(T_in - T) + (-ΔH_r)·r·V - U·A·(T T_cool). Это обеспечивает комплексный учет
тепловых потоков.
Значимость контроля теплопередачи
В экзотермических реакциях необходим
надёжный контроль теплоотвода, чтобы
избежать теплового взрыва. Значения
параметров U и ΔH_r критичны для
безопасности. Тщательный энергетический
баланс предотвращает аварии и оптимизирует
процесс.
7

8.

Баланс импульса и его
применение на практике
Уравнение Дарси-Вейсбаха связывает падение
давления с параметрами потока: Δp =
λ·(L/d)·(ρ·u²/2). Такой баланс позволяет учесть
влияние сопротивления в трубопроводах.
Коэффициент трения λ изменяется в зависимости
от режима потока (ламинарный или турбулентный).
Используется для расчета насосных мощностей и
масштабирования потоков с помощью критериев
подобия, таких как число Рейнольдса.
8

9.

Стохастические модели и источники
неопределённости
Учет случайных факторов
Метод Монте-Карло
Стохастические модели включают ошибки измерений,
которые принимаются как случайные величины с
нормальным распределением, параметры с
неопределенностью и флуктуации турбулентных
потоков, что отражает реальную вариабельность
процессов.
Для анализа влияния неопределённостей проводится
многократное моделирование с случайным
варьированием параметров (N≈1000). Это позволяет
получить статистические характеристики выходных
данных и повысить надежность предсказаний.
9

10.

Эмпирические модели и
регрессионный анализ
Характеристики и формы моделей
Эмпирические модели строятся на данных без физической
базы. Используются полиномиальные, степенные и
экспоненциальные функции, параметры которых
оцениваются методом наименьших квадратов для
аппроксимации зависимостей.
Оценка и ограничения
Коэффициент детерминации R² > 0.95 указывает на хорошее
соответствие модели данным. Однако экстраполяция
модели за пределы исходных данных опасна и требует
осторожности при применении в новых условиях.
10

11.

Уравнение Аррениуса: температурная
зависимость кинетики
Уравнение Аррениуса выражает зависимость
константы скорости реакции от температуры: k(T)
= A·exp(-E_a/(R·T)), где E_a — энергия активации,
а A — предэкспоненциальный множитель,
отражающий частоту столкновений молекул.
При увеличении температуры на 10 К скорость
реакций обычно возрастает в 2–4 раза. Так, для
перекиси водорода (E_a = 65 кДж/моль) скорость
удваивается при повышении температуры примерно
на 6 К, что подтверждает практическое применение
уравнения.
11

12.

Конверсия в CSTR при различных
параметрах τ и k
Таблица демонстрирует зависимость конверсии X_A от
времени пребывания τ при фиксированной константе
скорости реакции k = 1.5 ч⁻¹. Представлена формула
стационарного баланса и практические значения.
Конверсия возрастает с увеличением τ, однако
наблюдается снижение отдачи прироста с ростом
времени пребывания, что важно учитывать при
оптимизации процессов.
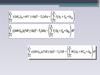
Стационарный материальный баланс реактора идеального смешивания (CSTR)
12

13.

Конверсия и эффективность PFR
в сравнении с CSTR
1. В реакторе идеального вытеснения (PFR)
конверсия рассчитывается по формуле X_A = 1 exp(-k·τ). При k·τ = 2 эффективность PFR
достигает 86.5%, что значительно превышает
CSTR, где X_A = 66.7%.
2. Важной особенностью PFR является отсутствие
перемешивания в поперечном направлении, что
позволяет молекулам иметь одинаковое время
пребывания, обеспечивая более высокий выход
продукта по сравнению с CSTR при равных условиях.
13

14.

Закон теплоотдачи Ньютона-Рихмана и
его параметры
Основное уравнение теплопередачи
Теплопередача описывается уравнением Q = h·A·(T_s T_f), где h — коэффициент теплоотдачи, а A — площадь
теплообмена. Эта формула применяется для оценки
тепловых потоков в химико-технологических процессах.
Коэффициенты теплоотдачи и критерии подобия
Значения коэффициента h варьируются: воздух — 5-25 Вт/(м²·К),
вода — 1000-10000 Вт/(м²·К), кипящая вода — до 100000 Вт/(м²·К).
Для расчёта h применяются числовые корреляции с использованием
критериев подобия, таких как число Нуссельта и корреляции
Диттуса-Боэлерта.
14

15.

Требования к математическим моделям:
адекватность и предсказательная
способность
Модель должна обеспечивать высокий
коэффициент детерминации R² > 0.95 и иметь
нормально распределённые остатки, а также
корректно учитывать физические ограничения,
такие как неотрицательность концентраций и
температуры.
Предсказательная способность подтверждается
сопоставлением значений RMSE на обучающей
и тестовой выборках, при этом RMSE должен
составлять менее 5% от среднего значения, что
свидетельствует о надёжности модели.
15

16.

Дополнительные требования к моделям:
робастность, простота, вычисления
Таблица раскрывает ключевые критерии выбору модели:
робастность, интерпретируемость, экстраполяцию и
вычислительную эффективность с кратким объяснением
их значимости для практического применения.
Для успешного моделирования необходимо учитывать
баланс между точностью, понятностью модели и
затратами времени на расчёт.
Лекция по математическому моделированию химико-технологических процессов
16

17.

Практический пример: синтез аммиака и его
моделирование
Механизм реакции и кинетика
Реакция синтеза аммиака N₂ + 3H₂ ⇌ 2NH₃
экзотермическая и достигает равновесия. Для
описания кинетики используется уравнение
Аррениуса, а также учитываются обратные реакции,
что позволяет моделировать скорость и выход
продукта.
Материальный и энергетический балансы
В модели учитываются материальный баланс с учётом
скорости реакции и потоков, а также энергетический
баланс, в котором контролируется температура реактора с
помощью охлаждающей системы для предотвращения
перегрева и поддержания оптимальных условий.
Промышленные условия и ограничение
выхода
В промышленности применяется железный катализатор при
температуре 400-450 К и давлении 150-300 атм. При этих
параметрах выход аммиака ограничен равновесием и
составляет 15-20%. Контроль температуры является
ключевым фактором эффективности и безопасности
процесса.
17

18.

Выбор типа реактора в зависимости от
параметров процесса
1. Быстрые реакции требуют применения CSTR
с равномерным перемешиванием для
поддержания постоянных условий реакционной
среды. Это обеспечивает однородность и
управляемость процесса.
2. Для медленных реакций чаще выбирают PFR, где
достигается максимальная конверсия за счёт отсутствия
перемешивания. Для дорогих реагентов
предпочтительны реакторы периодического действия с
целью минимизации потерь сырья.
18

19.

Инструменты и программное обеспечение
для моделирования
MATLAB и Octave
MathCAD
Python и SciPy
Специализированные пакеты
ПО MATLAB и его бесплатный аналог
Octave предоставляют мощные
функции решения ОДУ и ПДУ, включая
ode45 и bvp4c. Эти инструменты широко
используются для численного анализа
химико-технологических моделей.
MathCAD облегчает быстрое
выполнение инженерных расчетов,
используя rkadapt и Odesolve, что
делает его удобным для обучения
и простых моделирований без
глубокого программирования.
Python с библиотекой SciPy, включая
функции odeint и solve_ivp,
обеспечивает бесплатные и гибкие
инструменты для решения
дифференциальных уравнений, что
делает его популярным в научной
среде.
COMSOL и ANSYS Fluent предоставляют
возможности FEM и CFD соответственно
для сложных моделей. AspenPlus и HYSYS
используются в инженерной практике для
комплексного моделирования химических
процессов.
19

20.

Анализ чувствительности моделей:
методология и интерпретация
Анализ чувствительности оценивает изменение
выходного показателя модели в ответ на
вариации входных параметров ±10% с помощью
показателя эластичности S_i = (∂y/∂p_i)·(p_i/y),
выявляя наиболее влиятельные факторы.
Интерпретация результатов разделяет
чувствительность на слабую (|S_i|<0.5),
умеренную (0.5–2) и сильную (>2). Использование
диаграмм Парето позволяет приоритетизировать
параметры для оптимизации и точной калибровки
моделей.
20

21.

Множественные стационарные
состояния и бифуркация в химических
реакторах
В экзотермическом CSTR могут сосуществовать три
устойчивых режима: холодный с низкой
температурой и слабыми реакциями, горячий с
высокой температурой и интенсивным
тепловыделением, а также промежуточный
неустойчивый режим.
Переход между режимами зависит от начальных
условий и параметров системы. Контроль
параметров необходим для предотвращения рисков
теплового взрыва и аварийных состояний в процессе
эксплуатации.
21

22.

Оптимизация параметров химикотехнологического процесса
Оптимизация включает аналитические и численные
методы, способствующие повышению выхода и
снижению затрат. Используются динамическое
программирование и современные инструменты типа
MATLAB и COMSOL.
Оптимальное управление параметрами T, p, Q и
τ позволяет максимизировать выход продукции с
минимальными ресурсными затратами, что
важно для эффективности производства.
Лабораторные и промышленные исследования, 2023
22

23.

Масштабирование процессов:
критерии подобия и примеры
Гидродинамическое подобие через число
Рейнольдса
Число Рейнольдса Re = ρ·u·d/μ обеспечивает
гидродинамическое подобие при переходе от лабораторного к
промышленному реактору, гарантируя схожесть потоков и
режимов смешивания.
Дополнительные критерии и практические
примеры
Для корректного масштабирования необходимо учитывать также
числа Нуссельта, Прандтля и Дарси. Практический пример —
снижение скорости потока с 0.5 м/с до 0.05 м/с при увеличении
диаметра реактора в 10 раз.
23

24.

Неопределённость параметров и
оценка робастности модели
Основные источники неопределённости:
измерения с погрешностью ±2 К, варьирование
кинетических констант (k = 1.5 ± 0.3 м³/(моль·с))
и влияние загрязнений, не учтённых в модели.
Метод Монте-Карло с N=1000 прогонов
позволяет оценить средние значения и
стандартные отклонения выходных параметров,
визуализируя полосы неопределённости для
оценки надёжности и необходимости
корректировок.
24

25.

Типичные ошибки при построении
математических моделей
Основные ошибки — переобучение, неправильная
экстраполяция и пренебрежение физическими законами
приводят к снижению надёжности моделей. Приведены
рекомендации по их предотвращению.
Осознание и предотвращение этих ошибок критично для
разработки надёжных и предсказуемых математических
моделей.
Обзор литературы по моделированию, 2023
25

26.

Алгоритм выбора типа
математической модели
Решение строится от наличия фундаментальных
законов к выбору детерминированной модели,
при их отсутствии — к эмпирической или
экспериментальной модели.
Структурированный подход обеспечивает
адекватность модели, включая проверку
валидности и учёт случайных факторов.
Учебные материалы по моделированию, 2023
26

27.

Итоговая классификация математических
моделей
Детерминированные модели:
фундаментальный подход
Основаны на физических законах сохранения, обладают
обоснованной экстраполяцией. Примеры — ODE для
CSTR и PDE для PFR, обеспечивают высокую
надёжность и универсальность.
Стохастические модели и
неопределённость
Учитывают вероятностные элементы и неопределённость
параметров с помощью методов Монте-Карло и
стохастических дифференциальных уравнений, повышая
надёжность прогноза.
Эмпирические модели: данные без
физики
Базируются исключительно на экспериментальных
данных без физической основы, что ограничивает их
применение за пределами диапазона данных и
увеличивает риск ошибок.
Полуэмпирические модели: теория и
данные
Комбинируют физические основы и эмпирические
данные для повышения точности. Примером служит
модель Аррениуса, связанная с температурной
зависимостью реакций.
27

28.

Ключевые выводы по моделированию
химико-технологических процессов
Математические модели — фундамент инженерных
расчётов, выбор зависит от данных, знания физики
и необходимой точности. Детерминированные
модели обеспечивают надёжность и
универсальность.
Для успешного применения обязательна
валидация, анализ чувствительности и
учитывание масштабных критериев Re, Nu, Pr,
Da для обеспечения корректности и
воспроизводимости результатов.
28

29.

Благодарность и рекомендации по
дальнейшему изучению
Спасибо за внимание к теме моделирования
химико-технологических процессов. Контактные
данные преподавателя и график консультаций
доступны для дополнительной поддержки
обучающихся.
Рекомендуется изучить работы Ушевой,
Вейнгеровой, Fogler и Levenspiel для углубления
знаний. Поощряются вопросы и дискуссии для
лучшего понимания сложных аспектов темы.
29

30.

Заключение и
перспективы развития
моделирования
Глубокое понимание классификации моделей повышает
эффективность проектирования. Совмещение
детерминированных и стохастических методов расширяет
аналитические возможности и способствует устойчивому
развитию отрасли.