Арбелос Архимеда

1.

«АРБЕЛОС АРХИМЕДА»

2.

Геометрия - одна из самых древних
наук, она возникла очень давно, еще до
нашей эры. Возможно, на фоне
удивительных достижений науки и
техники она может показаться каким
– то малосовременным,
неразвивающимся предметом, не
нужным современному человеку.

3.

Архимед жил в III столетии
до н. э. в городе Сиракузы на
Сицилии, бывшим в то время
греческой колонией.
Много
прекрасных
открытий и изобретений
сделал
Архимед за свою
долгую жизнь.
АРХИМЕД
Будучи уже зрелым ученым,
в 50 лет, он увлекся (287 до н.э. – 212 до н.э.)
геометрией и не расставался
с ней до конца своих дней.

4.

ЦЕЛЬ:
Используя исторический подход,
познакомиться с геометрической
фигурой арбелосом и рассмотреть её
свойства

5.

ЗАДАЧИ:
•Познакомиться с понятием арбелоса.
•Рассмотреть леммы Архимеда.
•Рассмотреть решение задачи Архимедом и
современным учеником.
•Применить
полученные
решении задач на окружности.
знания
при

6.

АРБЕЛОС
В своих занятиях геометрией Архимед много
внимания уделял изучению свойств фигуры, носящей
название арбелос, или скорняжный нож.
Это название фигура получила из – за сходства с
очертаниями ножа, использовавшегося скорняками для
разделки кожи.

7.

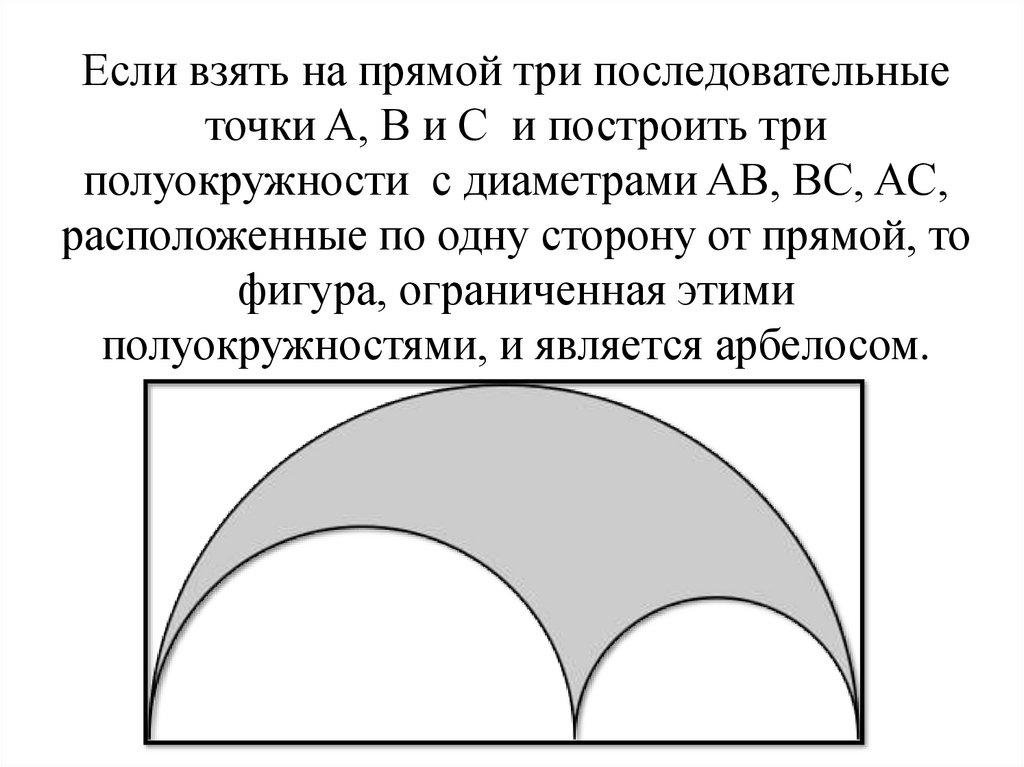
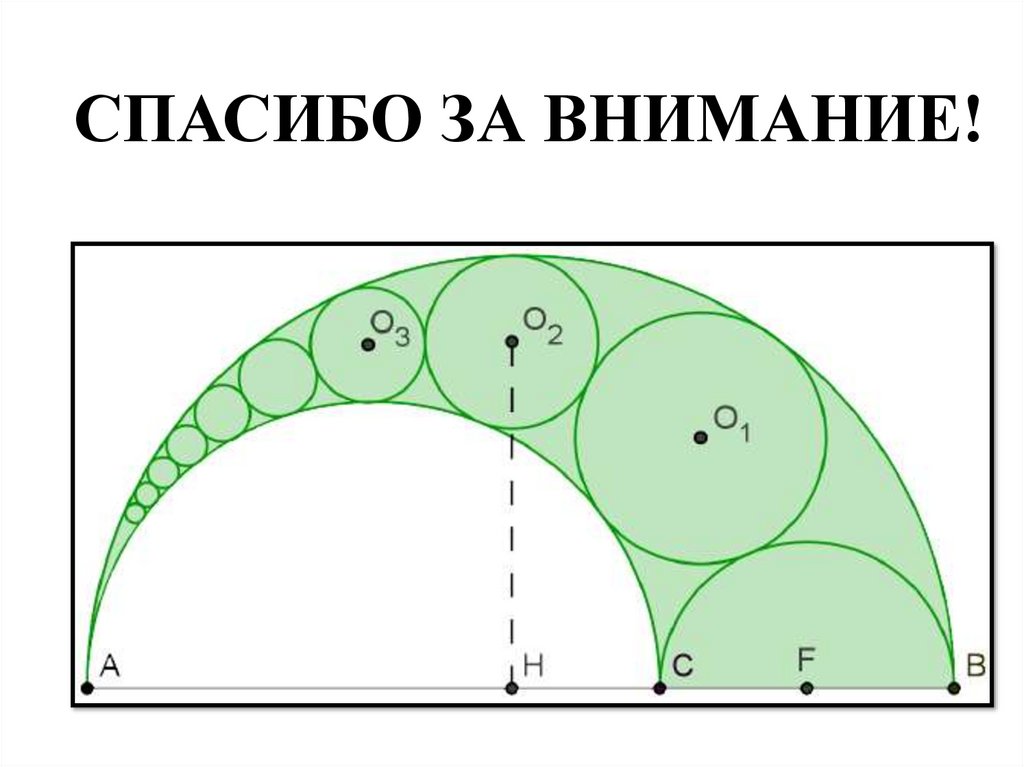
Если взять на прямой три последовательные
точки A, B и C и построить три
полуокружности с диаметрами AB, BC, AC,
расположенные по одну сторону от прямой, то
фигура, ограниченная этими
полуокружностями, и является арбелосом.

8.

Задача
На отрезке AB взята точка C. На отрезках AC, BC и AB,
как на диаметрах, в одной полуплоскости построены
полуокружности s1, s2 и s соответственно. Из точки C
восстановлен
перпендикуляр
к
прямой
AB,
пересекающий окружность s в точке D. В два
образовавшихся криволинейных треугольника вписаны
окружности α и β: первая касается отрезка CD,
полуокружности s1 и дуги AD, вторая — отрезка CD,
полуокружности s2 и дуги BD. Докажите, что две эти
вписанные окружности равны.

9.

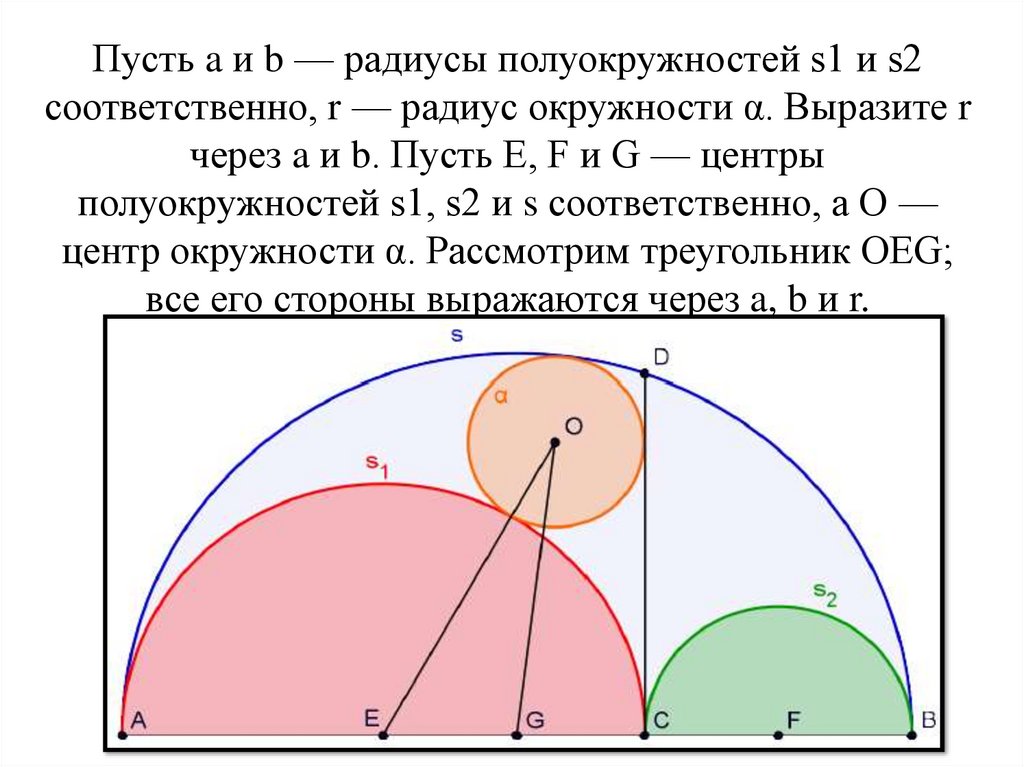
Пусть a и b — радиусы полуокружностей s1 и s2
соответственно, r — радиус окружности α. Выразите r
через a и b. Пусть E, F и G — центры
полуокружностей s1, s2 и s соответственно, а O —
центр окружности α. Рассмотрим треугольник OEG;
все его стороны выражаются через a, b и r.

10.

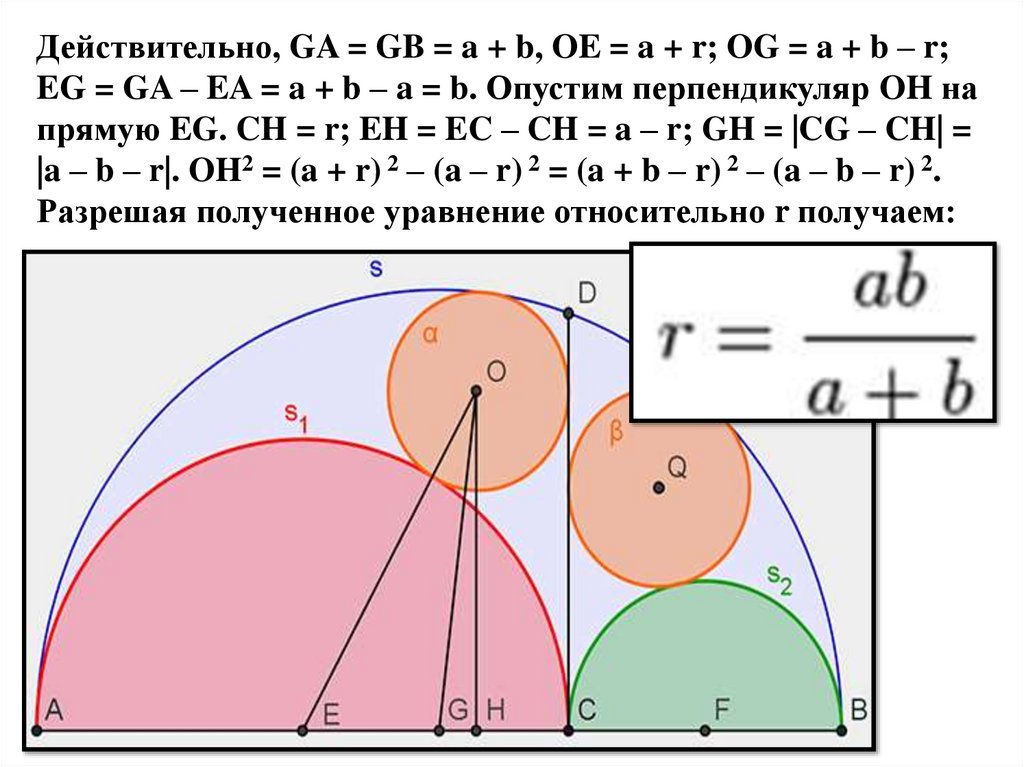
Действительно, GA = GB = a + b, OE = a + r; OG = a + b – r;
EG = GA – EA = a + b – a = b. Опустим перпендикуляр OH на
прямую EG. CH = r; EH = EC – CH = a – r; GH = |CG – CH| =
|a – b – r|. OH2 = (a + r) 2 – (a – r) 2 = (a + b – r) 2 – (a – b – r) 2.
Разрешая полученное уравнение относительно r получаем:

11.

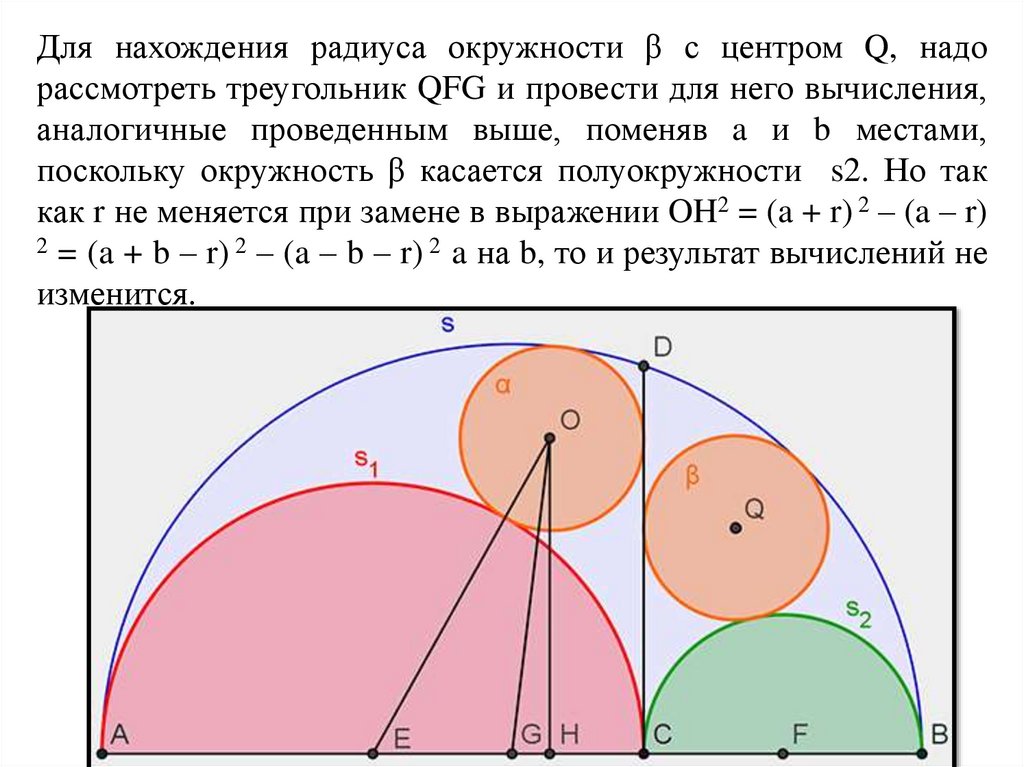
Для нахождения радиуса окружности β с центром Q, надо
рассмотреть треугольник QFG и провести для него вычисления,
аналогичные проведенным выше, поменяв a и b местами,
поскольку окружность β касается полуокружности s2. Но так
как r не меняется при замене в выражении OH2 = (a + r) 2 – (a – r)
2 = (a + b – r) 2 – (a – b – r) 2 a на b, то и результат вычислений не
изменится.

12.

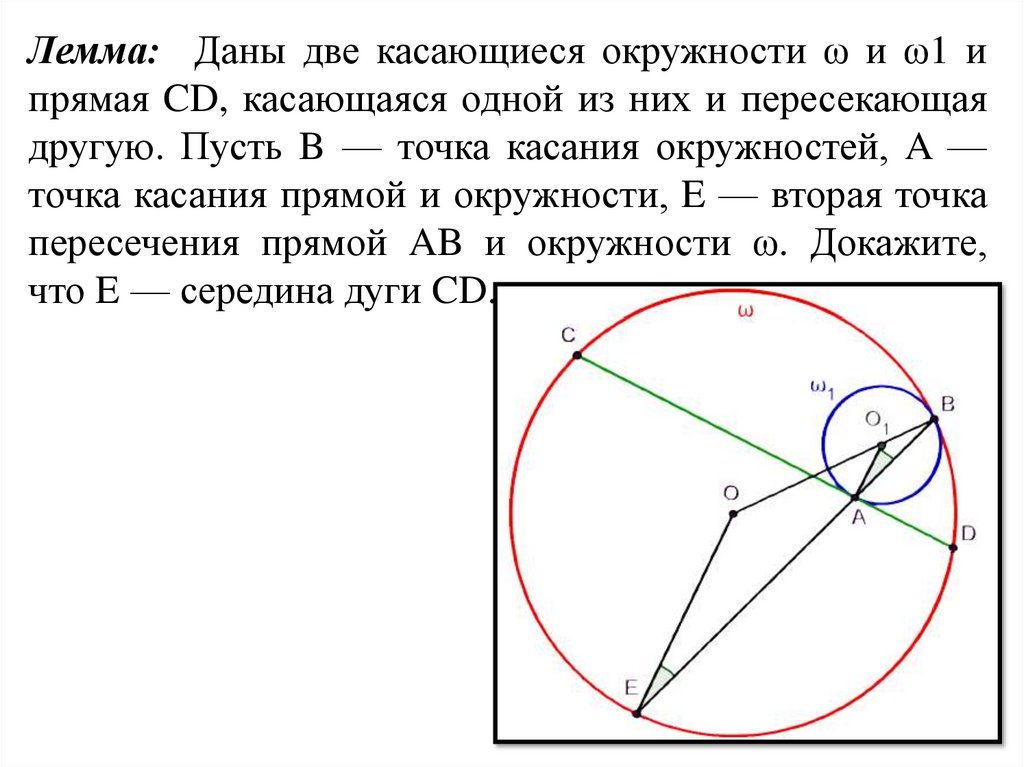
Лемма: Даны две касающиеся окружности ω и ω1 и
прямая CD, касающаяся одной из них и пересекающая
другую. Пусть B — точка касания окружностей, A —
точка касания прямой и окружности, E — вторая точка
пересечения прямой AB и окружности ω. Докажите,
что E — середина дуги CD.

13.

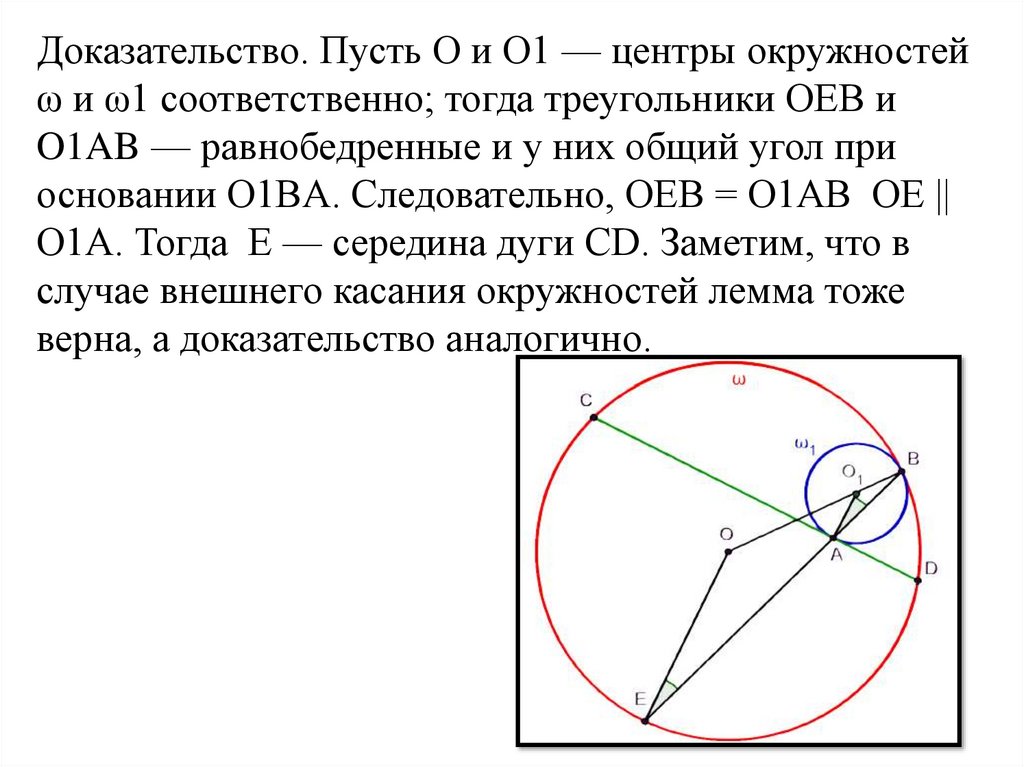
Доказательство. Пусть O и O1 — центры окружностей
ω и ω1 соответственно; тогда треугольники OEB и
O1AB — равнобедренные и у них общий угол при
основании O1BA. Следовательно, OEB = O1AB OE ||
O1A. Тогда E — середина дуги CD. Заметим, что в
случае внешнего касания окружностей лемма тоже
верна, а доказательство аналогично.

14.

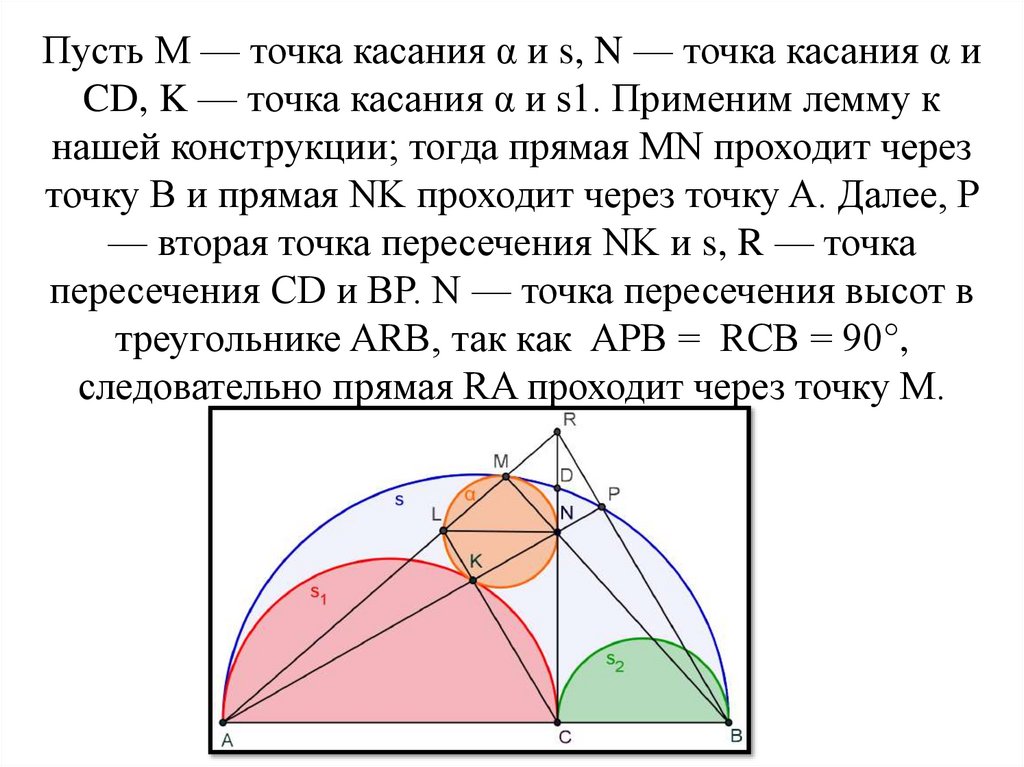
Пусть M — точка касания α и s, N — точка касания α и
CD, K — точка касания α и s1. Применим лемму к
нашей конструкции; тогда прямая MN проходит через
точку B и прямая NK проходит через точку A. Далее, P
— вторая точка пересечения NK и s, R — точка
пересечения CD и BP. N — точка пересечения высот в
треугольнике ARB, так как APB = RCB = 90°,
следовательно прямая RA проходит через точку M.

15.

Пусть L — вторая точка пересечения RA и α, тогда LKN = 90° (как угол,
опирающийся на диаметр), но AKC = 90° точки L, K и C лежат на одной
прямой.
LN — диаметр окружности α, следовательно LN || AB, следовательно
Заметим, что LC || RB, так как они перпендикулярны AP, следовательно
В обозначениях из первого решения полученное выражение принимает вид
и после сокращения общих множителей совпадает с выражением
.

16.

ЗАДАЧА:
Окружность радиуса r касается
изнутри окружности радиусом R.
Найдите радиус третьей, которая
касается обеих данных и прямой,
проходящей через их центры.

17.

O3
x
Решение:
O2H2 = (R – x)2 – x2 = R2 – 2RX = R(R – 2x)
O1H2 = (r + x)2 – x2 = r2 + 2rx
О1О2 = R – r = HO2 + HO1
x (r – R) + Rr =
*
x2(r – R)2 + R2r2 + 2xRr (r – R) =
(r2 + 2rx) (R2 – 2Rx)x2(r2 – 2rR + R2) +
R2r2 + 2xr2R –
2xrR2 = x2r2 – 2rRx2 + x2R2 + 4rRx2 =
4xR2r – 4xRr2
x2( r + R)2 = 4xRr (R – r)
x=
O1
H
O2

18.

СПАСИБО ЗА ВНИМАНИЕ!