Гомотетия (3)

1.

Гомотетия:
Преобразование подобия
Методическая разработка занятий для учащихся 8-9 классов. Изучаем
математическую модель масштабирования и её применение в
геометрии.

2.

Цели и задачи урока
Образовательные
Развивающие
Воспитательные
Введём определение гомотетии,
Разовьём пространственное
Воспитаем точность при
докажем её свойства и научимся
мышление, логику и навыки работы
выполнении чертежей и интерес к
строить образы фигур.
с чертёжными инструментами.
решению нестандартных задач.
Научимся определять центр и коэффициент гомотетии, а также применять эти знания для решения задач на построение и
доказательство.

3.

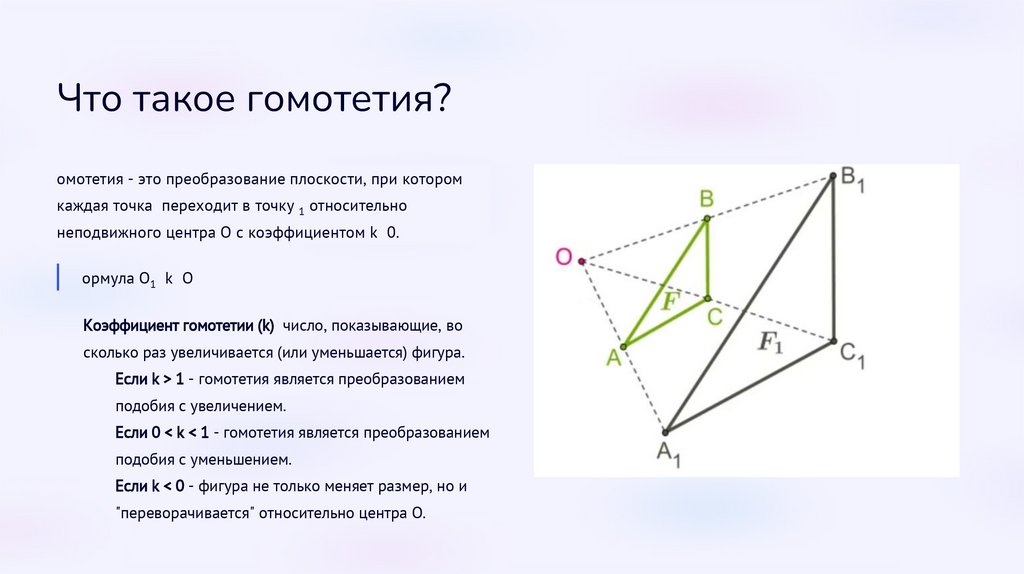
Что такое гомотетия?
Гомотетия - это преобразование плоскости, при котором
каждая точка X переходит в точку 1 относительно
неподвижного центра O с коэффициентом k 0.
Формула: OX1 k OX
Коэффициент гомотетии (k) число, показывающие, во
сколько раз увеличивается (или уменьшается) фигура.
Если k > 1 - гомотетия является преобразованием
подобия с увеличением.
Если 0 < k < 1 - гомотетия является преобразованием
подобия с уменьшением.
Если k < 0 - фигура не только меняет размер, но и
"переворачивается" относительно центра O.

4.

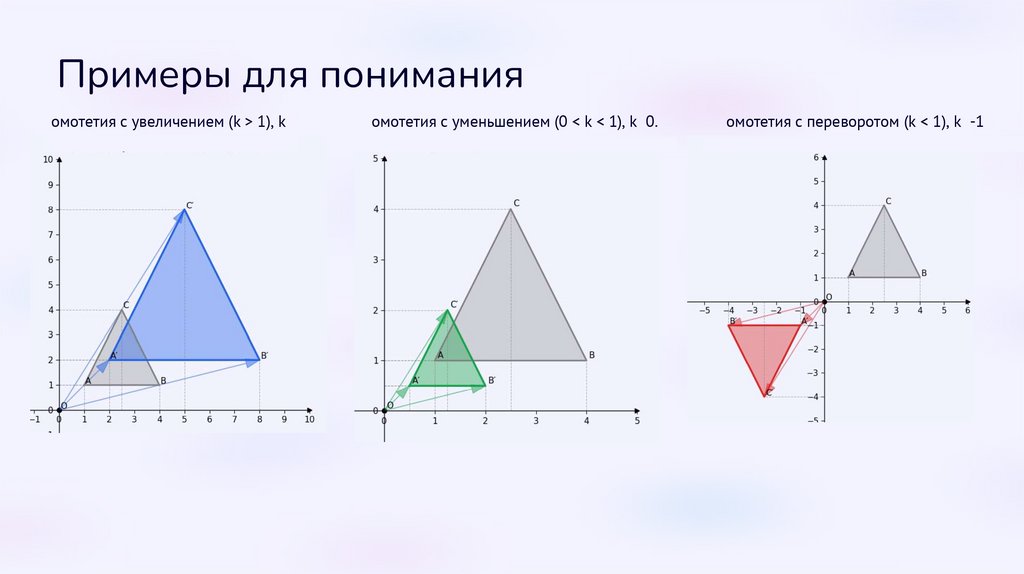
Примеры для понимания
Гомотетия с увеличением (k > 1), k = 2
Гомотетия с уменьшением (0 < k < 1), k = 0.5
Гомотетия с переворотом (k < 1), k = -1

5.

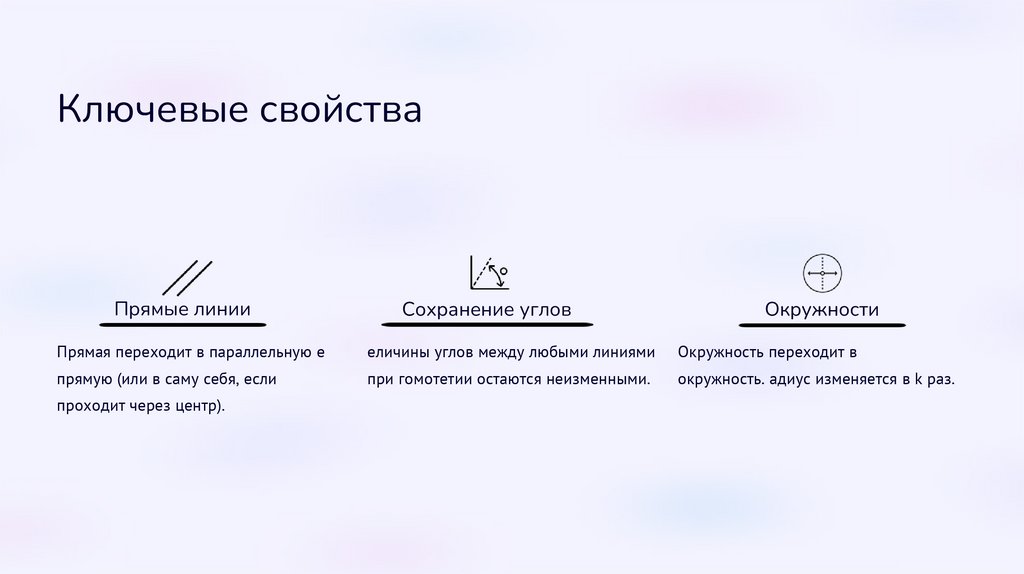
Ключевые свойства
Прямые линии
Сохранение углов
Окружности
Прямая переходит в параллельную ей
Величины углов между любыми линиями
Окружность переходит в
прямую (или в саму себя, если
при гомотетии остаются неизменными.
окружность. Радиус изменяется в k раз.
проходит через центр).

6.

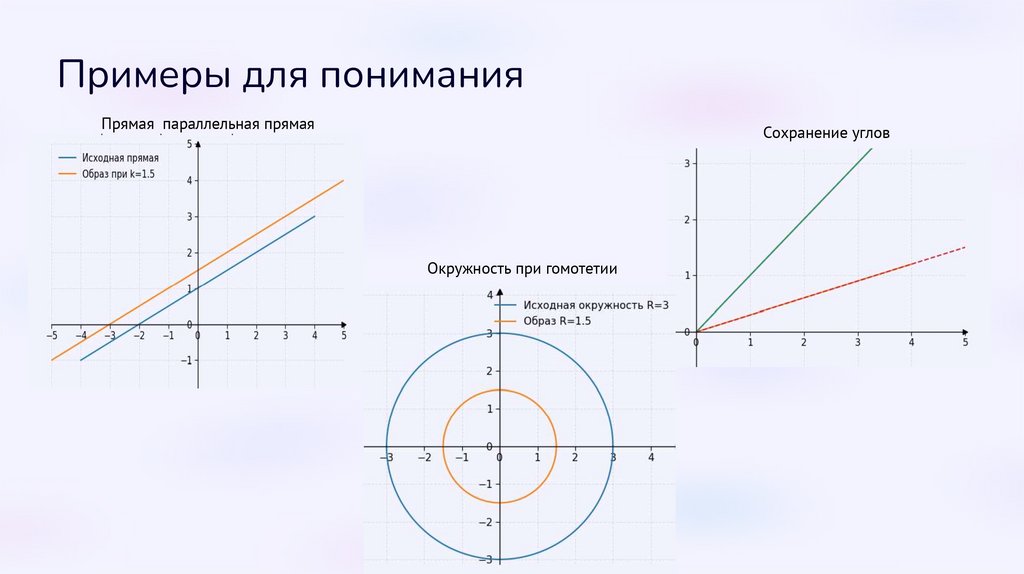
Примеры для понимания
Прямая параллельная прямая
Сохранение углов
Окружность при гомотетии

7.

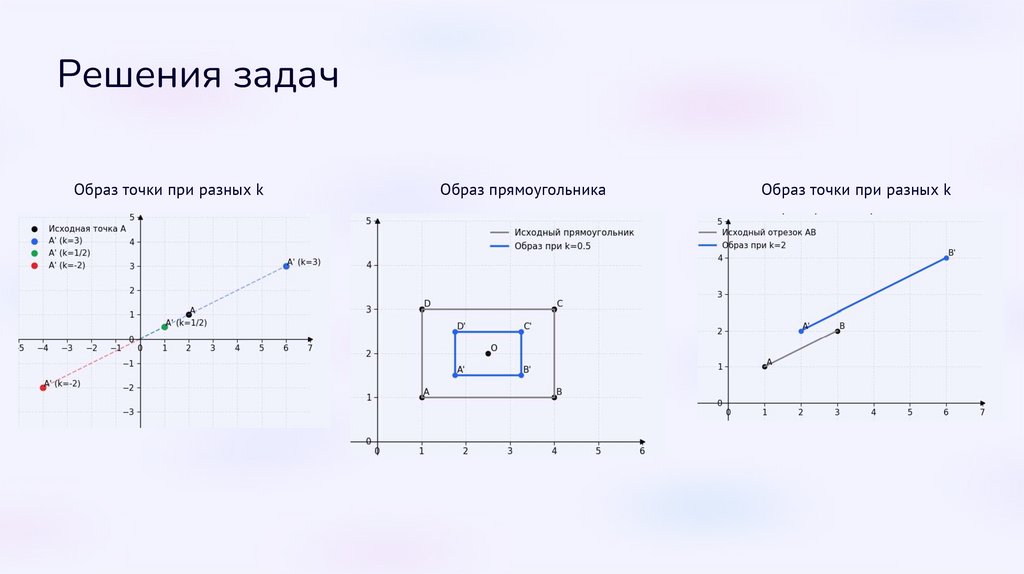
Блок 1: Базовые упражнения
Отработка определений и простейших построений.
Построение точек
Работа с отрезками
Фигуры
Постройте образ прямоугольника с
Постройте образ отрезка AB при k=2.
центром в пересечении диагоналей
Постройте образ точки A при центре
Проверьте равенство 11
и k=0.5.
O и коэффициентах k=3, k=1/2, k=-2.
.

8.

Решения задач
Образ точки при разных k
Образ прямоугольника
Образ точки при разных k

9.

Блок 2: Ключевые задачи
Проверим понимание гомотетии на практике, решая следующие задачи.
Нахождение коэффициента
по расстояниям
Известно, что при гомотетии центр O
точка перешла в ′. OA = 4 см, OA′ = 10
см. Найдите коэффициент k.
Стороны треугольника
после гомотетии
Треугольник ABC имеет
стороны 3, 4, 6. Выполнена гомотетия с
коэффи-циентом 2. Найдите стороны ′′C′.
Нахождение координатных
точек после гомотетии
A(2, 1). Центр гомотетии в начале
координат. Коэффициент k = -3.
Найдите ′.

10.

Решения задач
1. Нахождение коэффициента по расстояниям
2. Стороны треугольника после гомотетии
2
.
1
.
3. Нахождение координатных точек после
гомотетии
3.

11.

Блок 3: Обычные задачи
этом разделе мы закрепим наши знания, решая типовые задачи на гомотетию.
Радиус круга после гомотетии
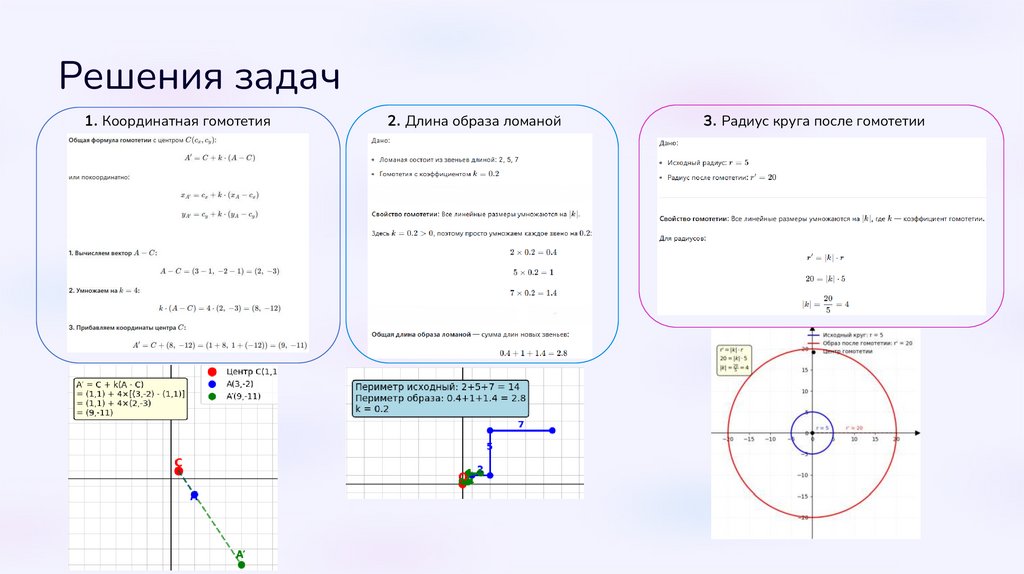
Координатная гомотетия
A(3, -2). Гомотетия с центром C(1,1) и
коэффициентом k = 4. Найдите ′.
Длина образа ломаной
Ломаная состоит из звеньев
длиной 2, 5, 7. Гомотетия с
коэффициентом k = 0.2.
Круг радиуса перешел в круг
радиуса 20.
Найдите коэффициент гомотетии.

12.

Решения задач
1. Координатная гомотетия
2. Длина образа ломаной
3. Радиус круга после гомотетии

13.

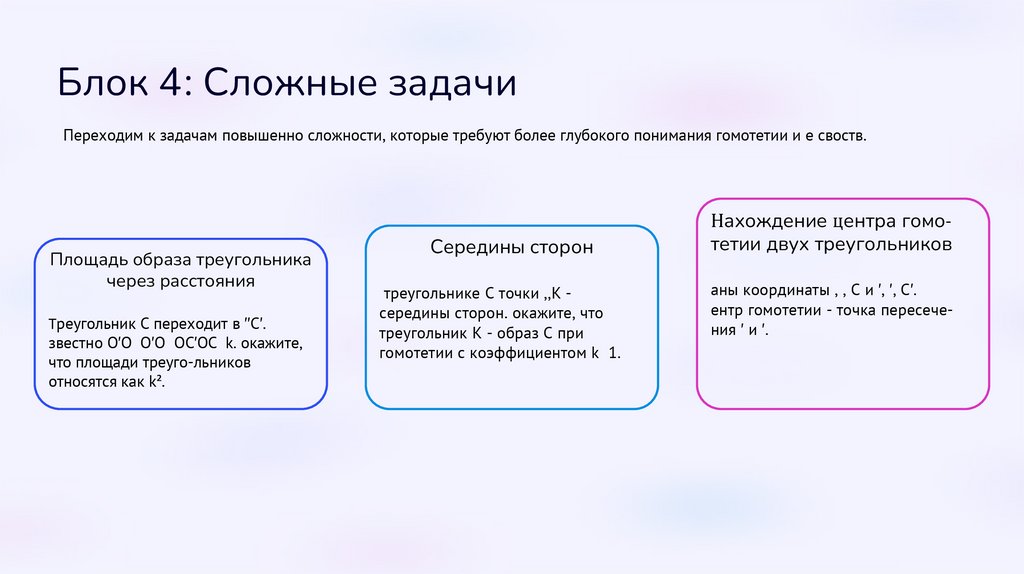
Блок 4: Сложные задачи
Переходим к задачам повышенной сложности, которые требуют более глубокого понимания гомотетии и её свойств.
Площадь образа треугольника
через расстояния
Треугольник ABC переходит в ′′C′.
Известно: OA′/OA = OB′/OB = OC′/OC = k. Докажите,
что площади треуго-льников
относятся как k².
Середины сторон
треугольнике ABC точки M,N,K середины сторон. Докажите, что
треугольник MNK - образ ABC при
гомотетии с коэффициентом k = 1/2.
Нахождение центра гомотетии двух треугольников
Даны координаты A, B, C и ′, B′, C′.
Центр гомотетии - точка пересечения ′ и ′.

14.

Решения задач
1. Площадь образа треугольника
через расстояния
2. Середины сторон
3. Нахождение центра
гомотетии двух треугольников

15.

Блок 5: Задачи на построение
Использование свойств гомотетии для сложных геометрических построений.
Вписанный квадрат
Касательная окружность
Деление отрезка
Впишите квадрат в острый
Постройте окружность, проходящую
С помощью только линейки
треугольник так, чтобы одна
через точку внутри угла и
постройте точку D такую, что AB : CD = 2 : 1.
сторона лежала на основании, а
касающуюся его сторон.
вершины на боковых сторонах.

16.

Решения задач
1. Вписанный квадрат
2. Касательная окружность
3. Деление
отрезка

17.

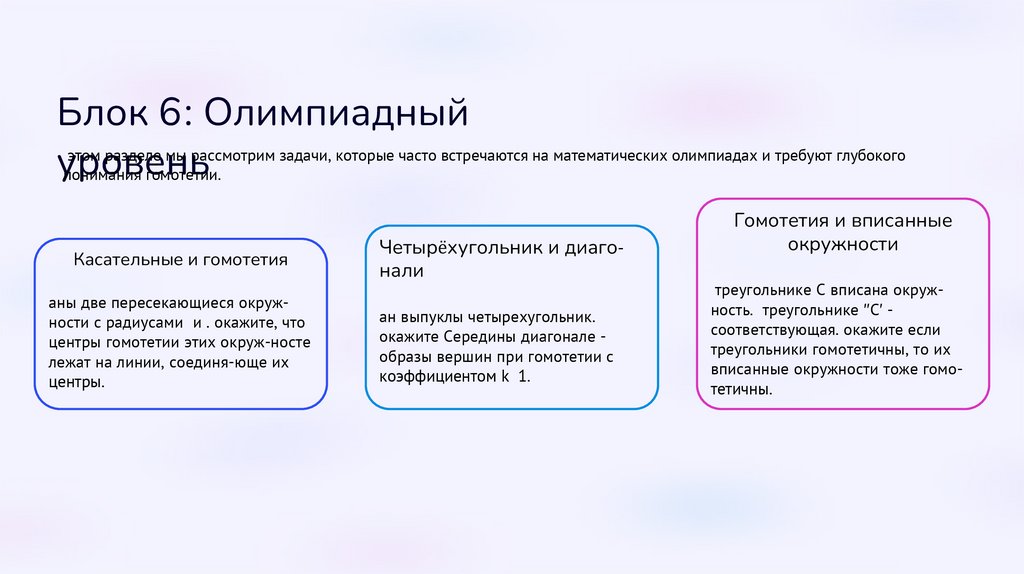
Блок 6: Олимпиадный
этом разделе мы рассмотрим задачи, которые часто встречаются на математических олимпиадах и требуют глубокого
уровень
понимания гомотетии.
Касательные и гомотетия
Даны две пересекающиеся окружности с радиусами и r. Докажите, что
центры гомотетии этих окруж-ностей
лежат на линии, соединя-ющей их
центры.
Четырёхугольник и диагонали
Дан выпуклый четырехугольник.
Докажите Середины диагоналей образы вершин при гомотетии с
коэффициентом k = 1/2.
Гомотетия и вписанные
окружности
треугольнике ABC вписана окружность. треугольнике ′′C′ соответствующая. Докажите если
треугольники гомотетичны, то их
вписанные окружности тоже гомотетичны.

18.

Решения задач
1. Касательные и гомотетия
2. Четырёхугольник и
диагонали
3. Гомотетия и вписанные
окружности

19.

Задачи для самостоятельного решения
1. Стороны треугольника после гомотетии
2. Свойство центров гомотетии
Треугольник ABC имеет стороны 3, 4, 6. Выпол-нена
гомотетия с коэффициентом 2. Найдите сто-роны ′′C′.
Даны два подобных треугольника ABC и ′′C′,
расположенные так, что вершины лежат на
прямых ′, B′, CC′. Докажите, что эти прямые
пересекаются в точке - центре гомотетии.
3. Где находится изображение точки
4. Найти центр гомотетии двух треугольников
OA = 12 см. Гомотетия с k = -1/4. Найдите OA′ и расположение A′.
Даны координаты A, B, C и ′, ′B , C′. Центр гомо-тетии точка пересечения ′ и ′.

20.

Литература и ресурсы
Учебники
Атанасян Л.С. "Геометрия. 7-
Дополнительно
Васильев Н.Б. "Прямые и кривые"
классы"
Погорелов А.В. "Геометрия. 7-
Интернет-ресурс: math.ru
классы"
Материалы для подготовки к ОГЭ
Шарыгин И.Ф. "Геометрия. 7-9 классы"
и ЕГЭ