6.1. Прямые и плоскости в пространстве

1. Прямые и плоскости в пространстве

2. Геометрия

Планиметрия
Изучает свойства
геометрических
фигур на
плоскости
Стереометрия
Изучает свойства
геометрических
тел в пространстве

3. Начальные понятия стереометрии

4.

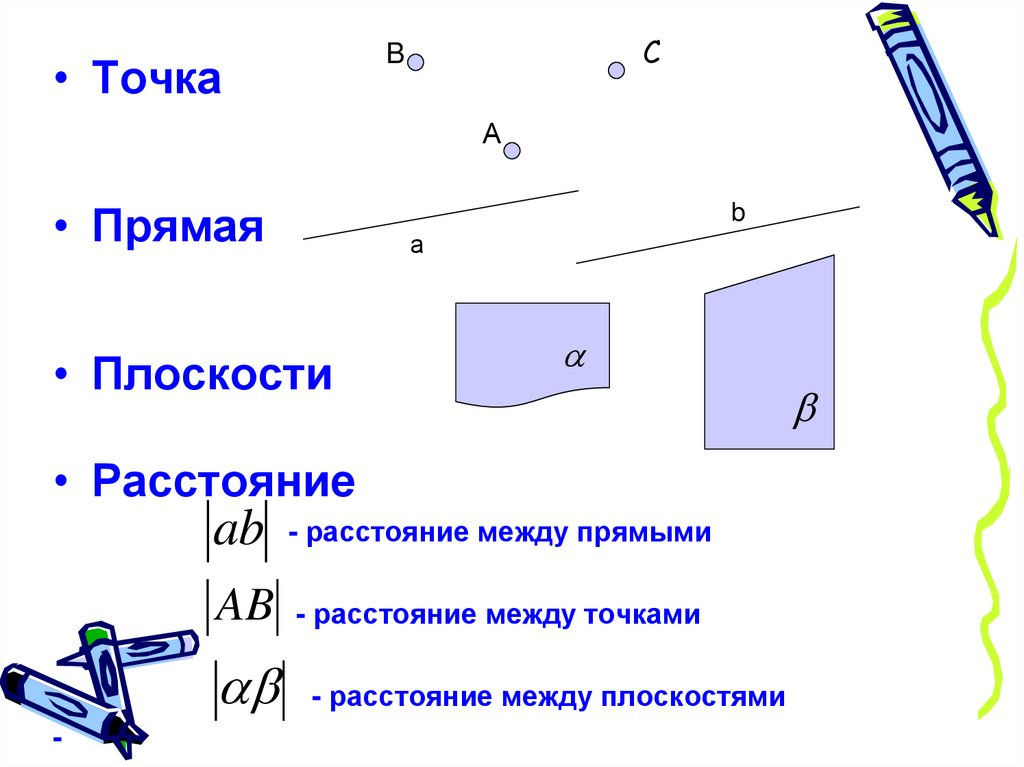
• Точка
C
B
А
• Прямая
• Плоскости
b
а
• Расстояние
ab - расстояние между прямыми
AB - расстояние между точками
- расстояние между плоскостями
-

5. Аксиомы стереометрии

6.

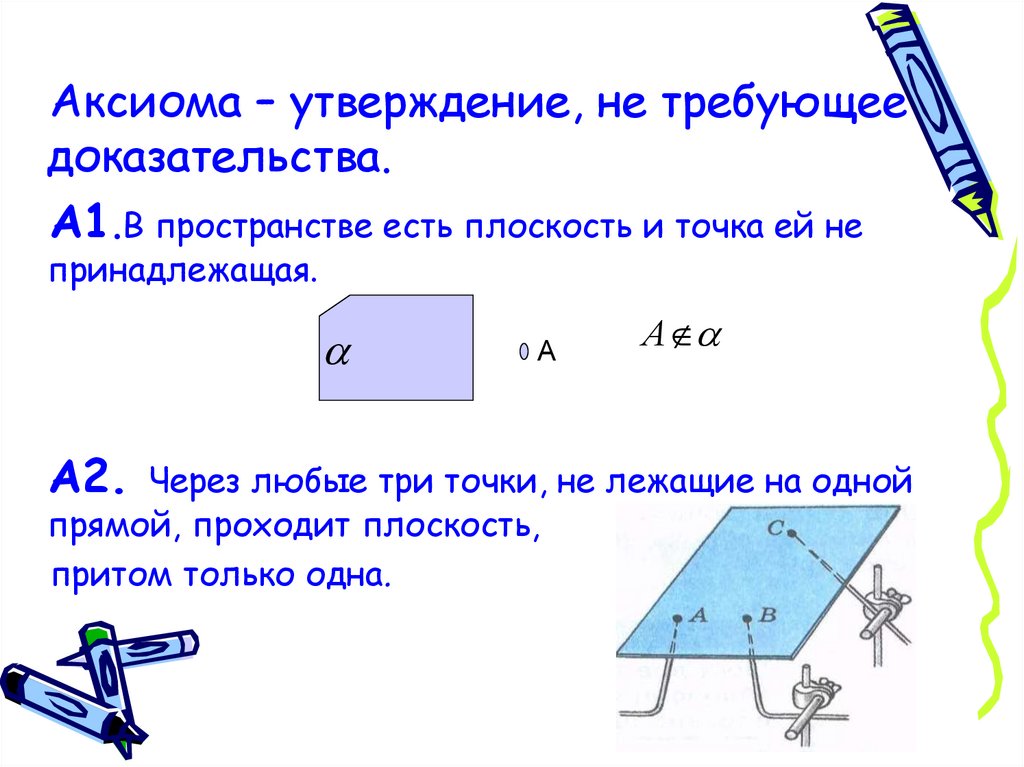
Аксиома – утверждение, не требующее
доказательства.
А1.В пространстве есть плоскость и точка ей не
принадлежащая.
А
А
А2. Через любые три точки, не лежащие на одной
прямой, проходит плоскость,
притом только одна.

7.

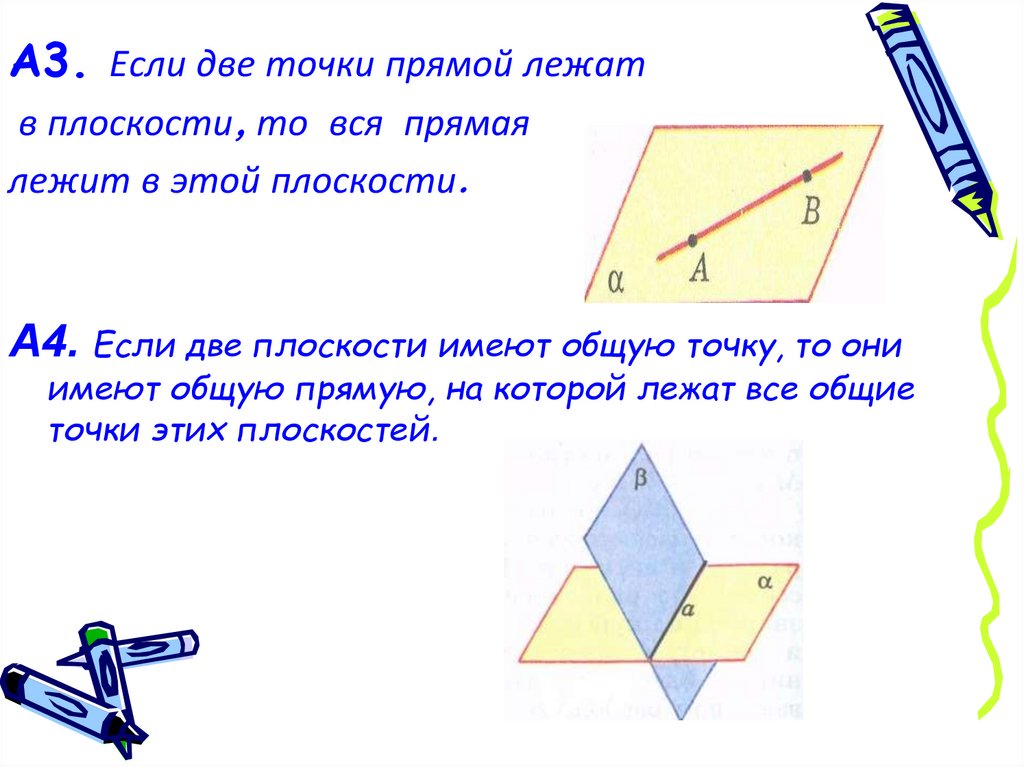
А3. Если две точки прямой лежат
в плоскости, то вся прямая
лежит в этой плоскости.
А4. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.

8. Следствия из аксиом

9.

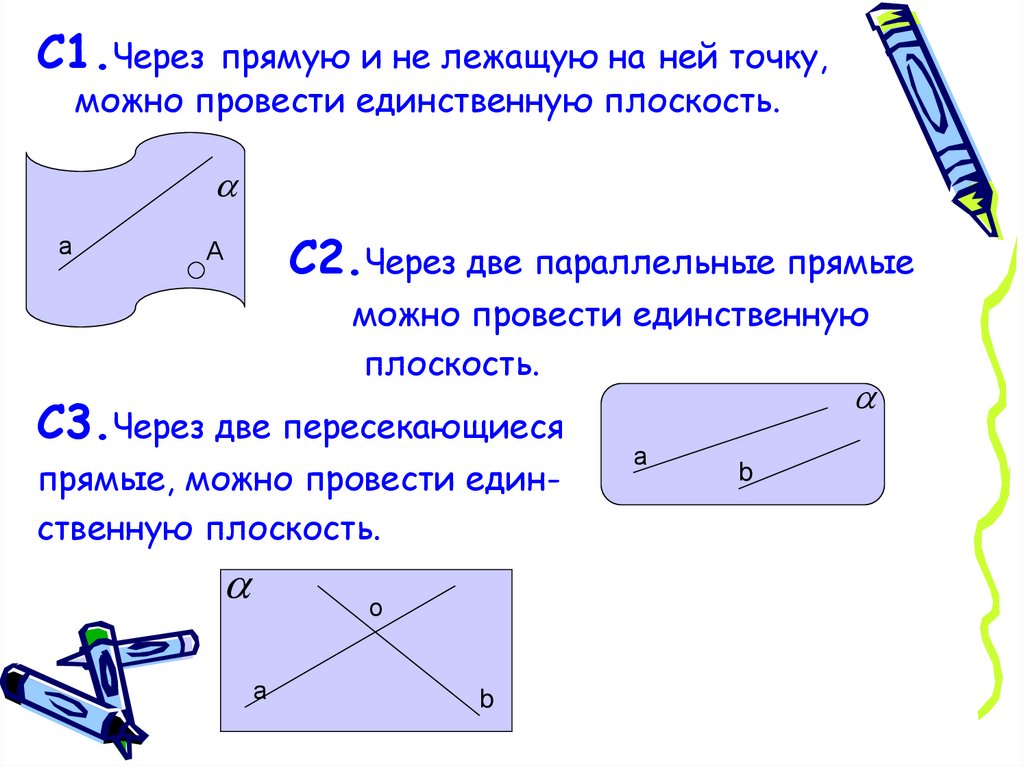
С1.Через прямую и не лежащую на ней точку,
можно провести единственную плоскость.
а
С2.Через две параллельные прямые
А
можно провести единственную
плоскость.
С3.Через две пересекающиеся
прямые, можно провести единственную плоскость.
о
а
b
а
b

10. Взаимное расположение прямых в пространстве

11. Прямые в пространстве могут располагаться:

А) Параллельно
Б) Пересекаться
В) Перпендикулярно
Г) Скрещиваться

12.

О1. Две прямые параллельны, если они
лежат в одной плоскости и не имеют
общих точек.
О2. Две прямые пересекаются, если они
лежат в одной плоскости и имеют одну
общую точку.
О3.Две прямые перпендикулярны, если
они пересекаются под прямым углом.
О4.Две прямые скрещиваются, если они
лежат в разных плоскостях.

13.

a
b
а
с
d
А
b
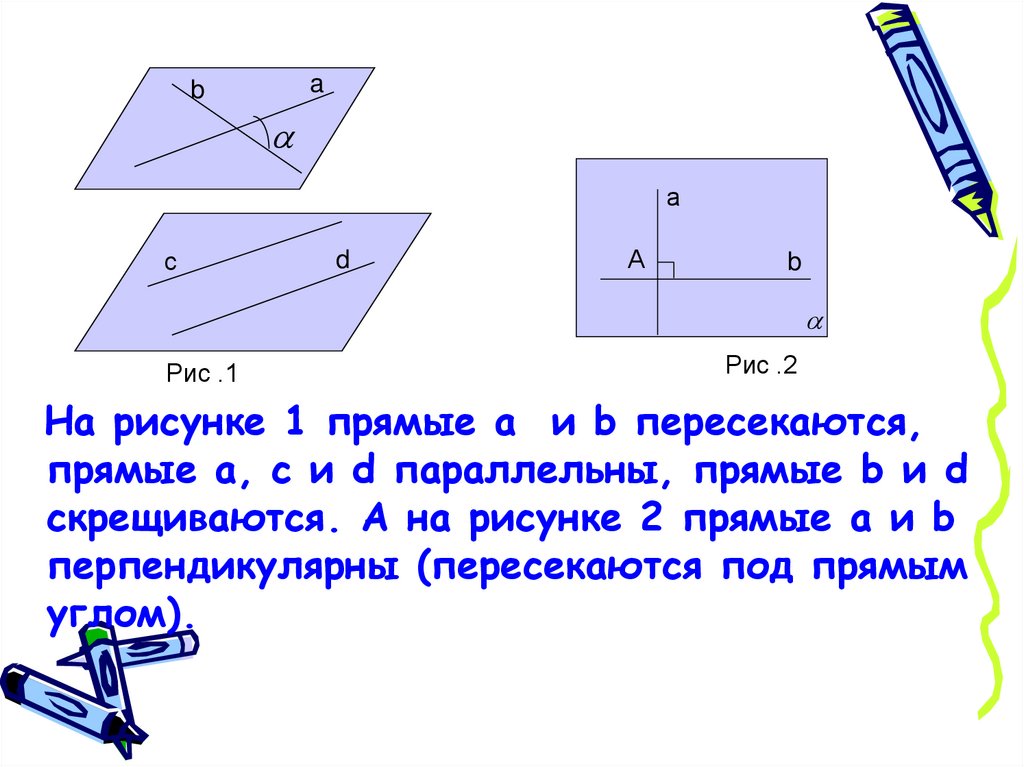
Рис .1
Рис .2
На рисунке 1 прямые a и b пересекаются,
прямые а, с и d параллельны, прямые b и d
скрещиваются. А на рисунке 2 прямые a и b
перпендикулярны (пересекаются под прямым
углом).

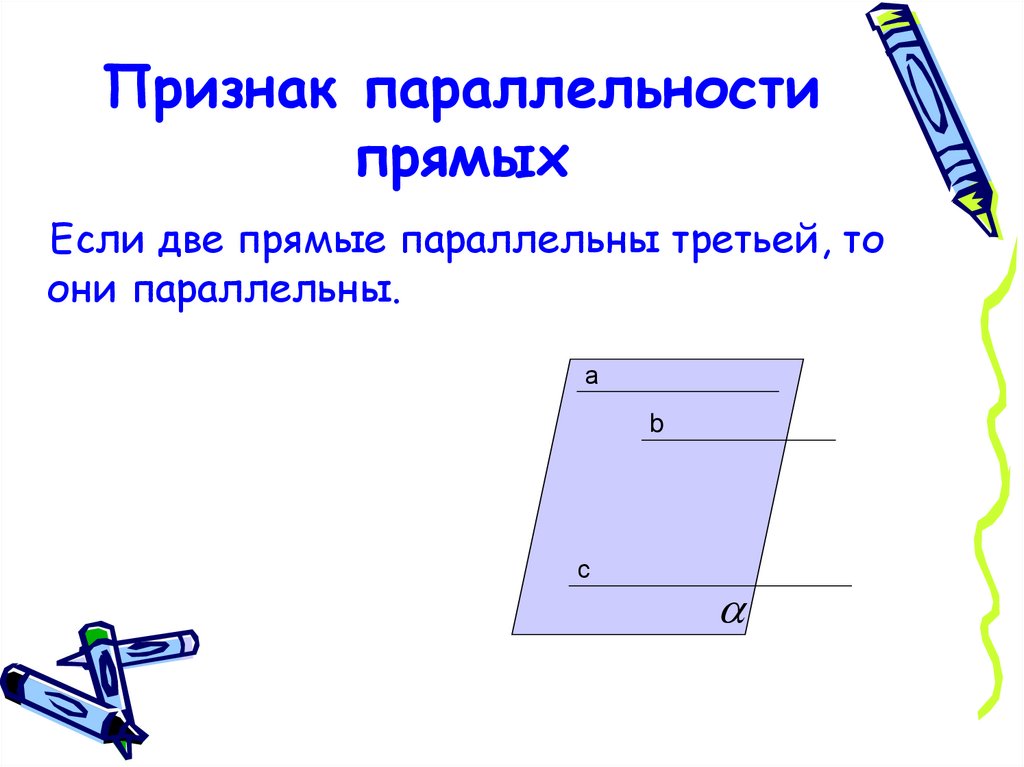
14. Признак параллельности прямых

Если две прямые параллельны третьей, то
они параллельны.
а
b
с

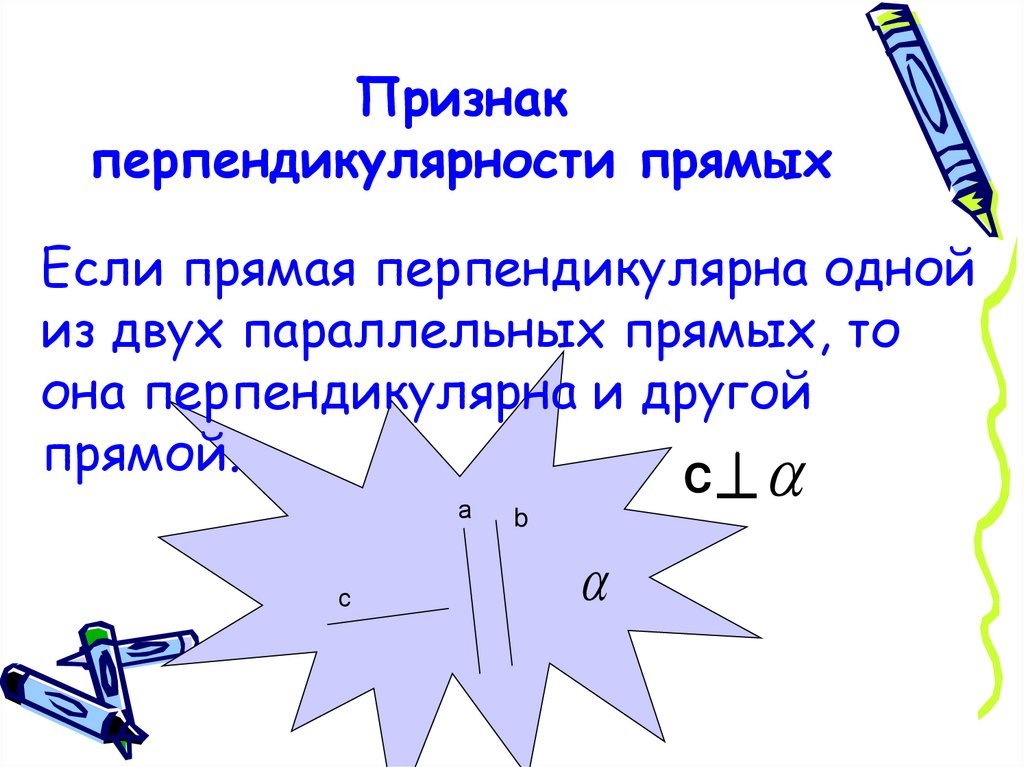
15. Признак перпендикулярности прямых

Если прямая перпендикулярна одной
из двух параллельных прямых, то
она перпендикулярна и другой
прямой.
C
а
с
b

16. Взаимное расположение прямой и плоскости

17.

Прямые и плоскости могут
располагаться:
А) Прямая лежит в плоскости
Б) Прямая параллельна плоскости
В) Прямая пересекает плоскость
Г) Прямая перпендикулярна плоскости

18.

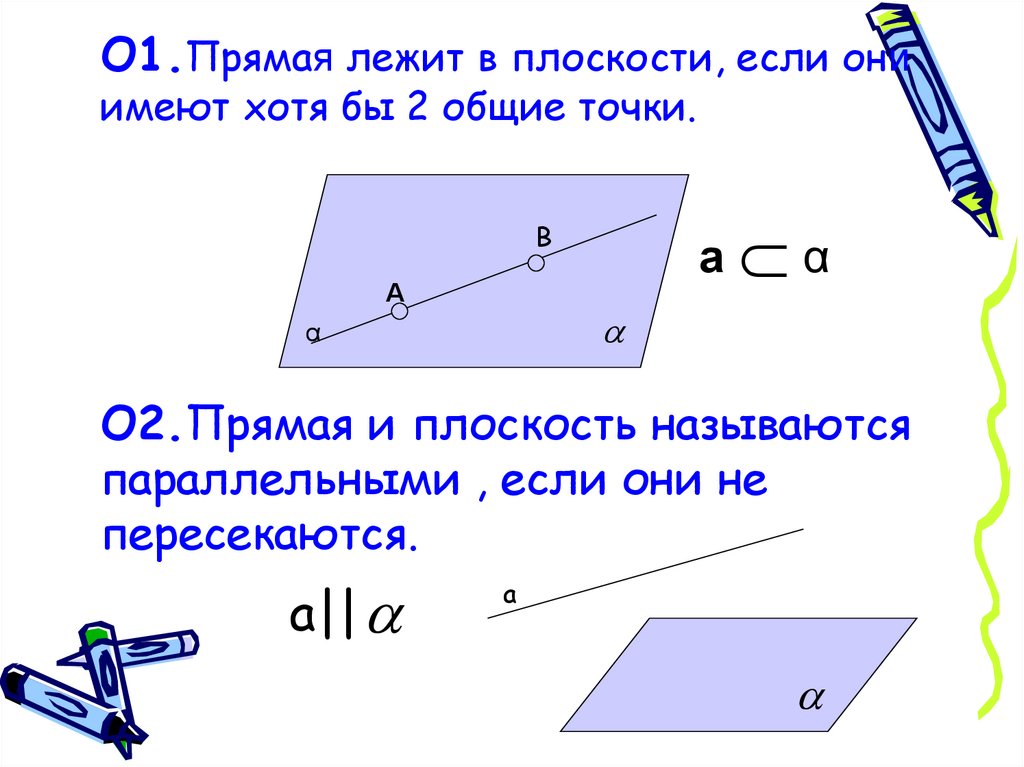
О1.Прямая лежит в плоскости, если они
имеют хотя бы 2 общие точки.
а α
B
А
α
О2.Прямая и плоскость называются
параллельными , если они не
пересекаются.
а||
а

19.

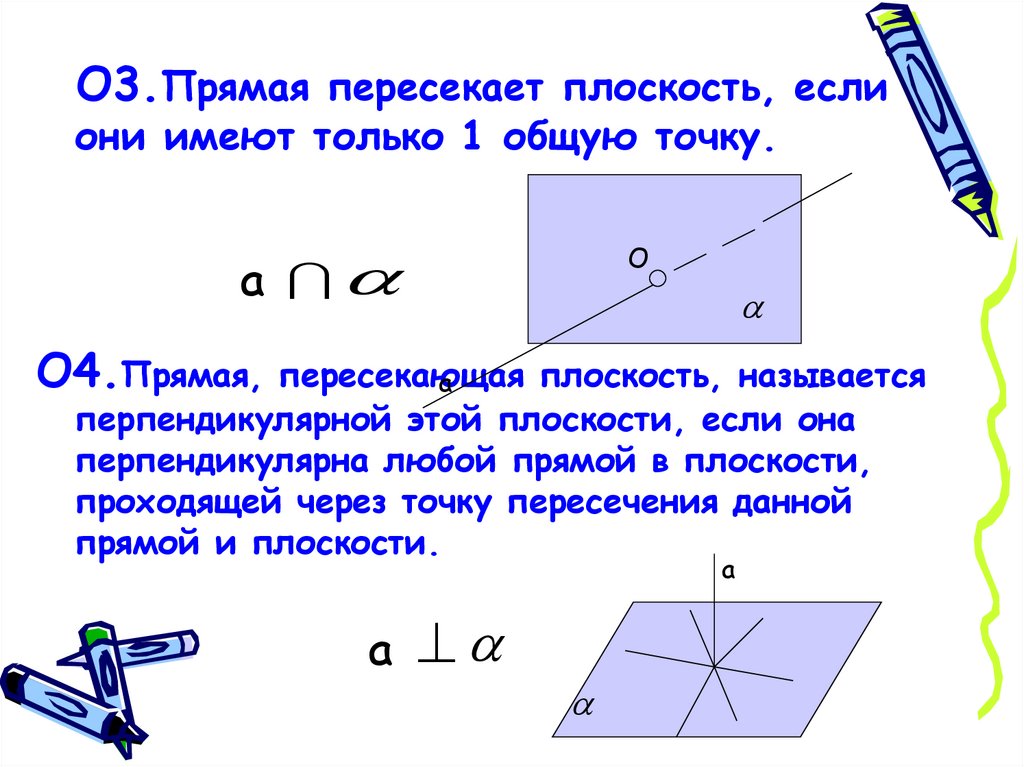
О3.Прямая пересекает плоскость, если
они имеют только 1 общую точку.
а
О
О4.Прямая, пересекающая
плоскость, называется
а
перпендикулярной этой плоскости, если она
перпендикулярна любой прямой в плоскости,
проходящей через точку пересечения данной
прямой и плоскости.
а
а

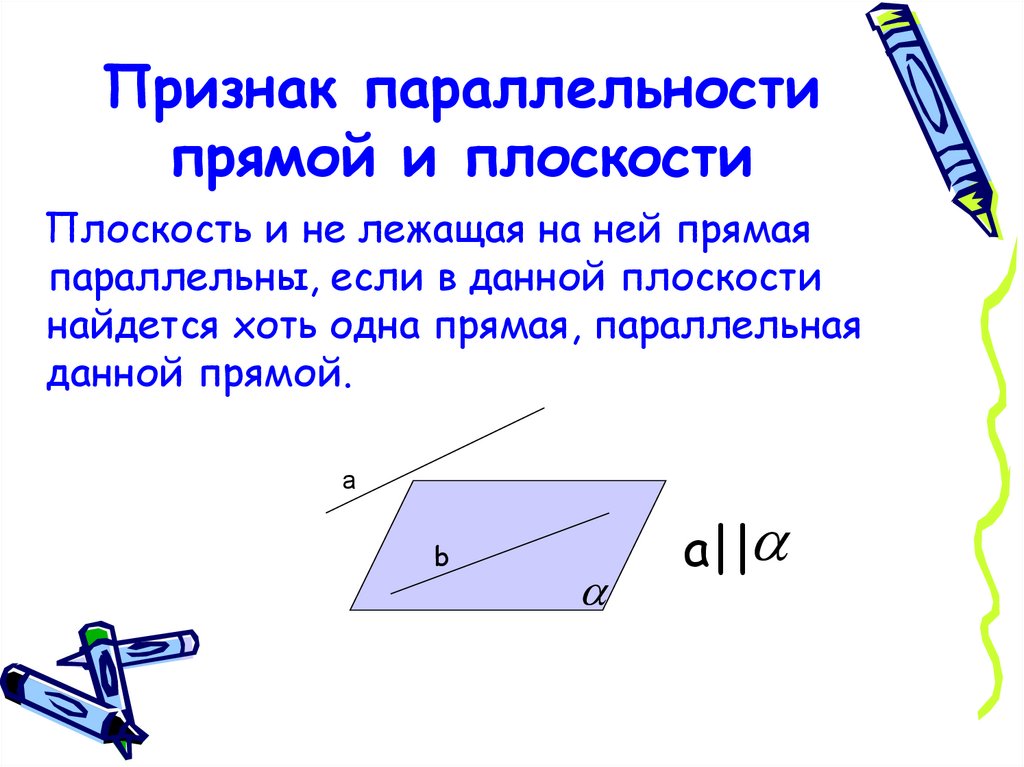
20. Признак параллельности прямой и плоскости

Плоскость и не лежащая на ней прямая
параллельны, если в данной плоскости
найдется хоть одна прямая, параллельная
данной прямой.
а
b
а||

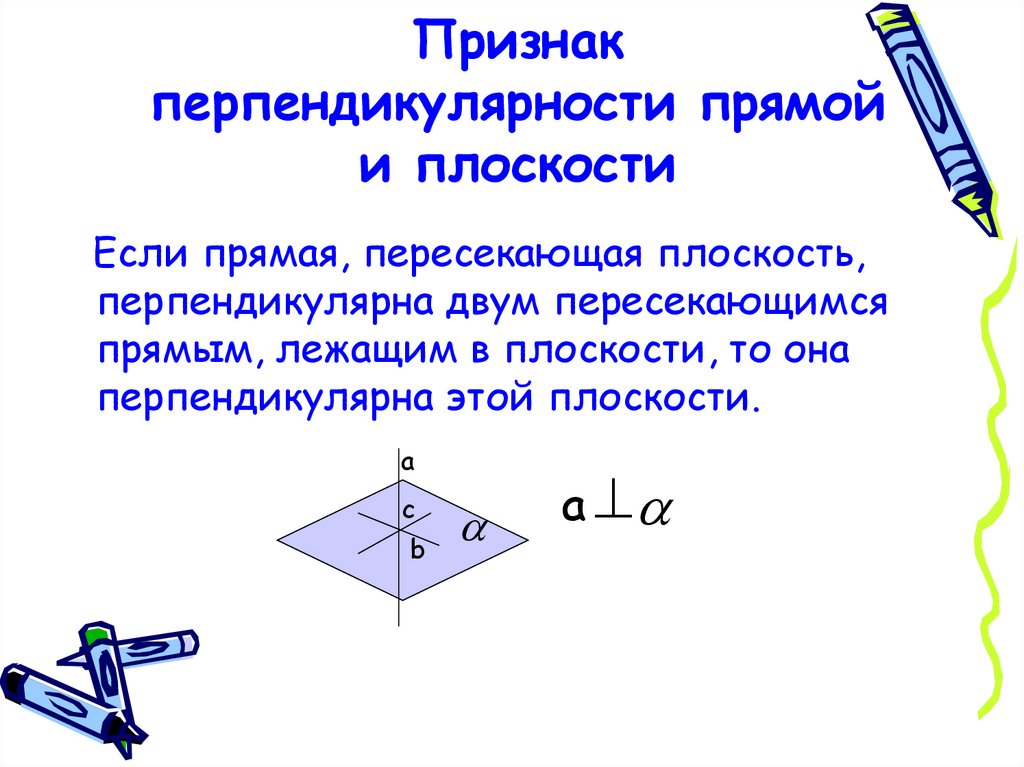
21. Признак перпендикулярности прямой и плоскости

Если прямая, пересекающая плоскость,
перпендикулярна двум пересекающимся
прямым, лежащим в плоскости, то она
перпендикулярна этой плоскости.
а
c
b
а

22. Взаимное расположение двух плоскостей

23.

Две плоскости в
пространстве могут
располагаться:
А) Параллельно
Б)Пересекаться
В)Перпендикулярно

24.

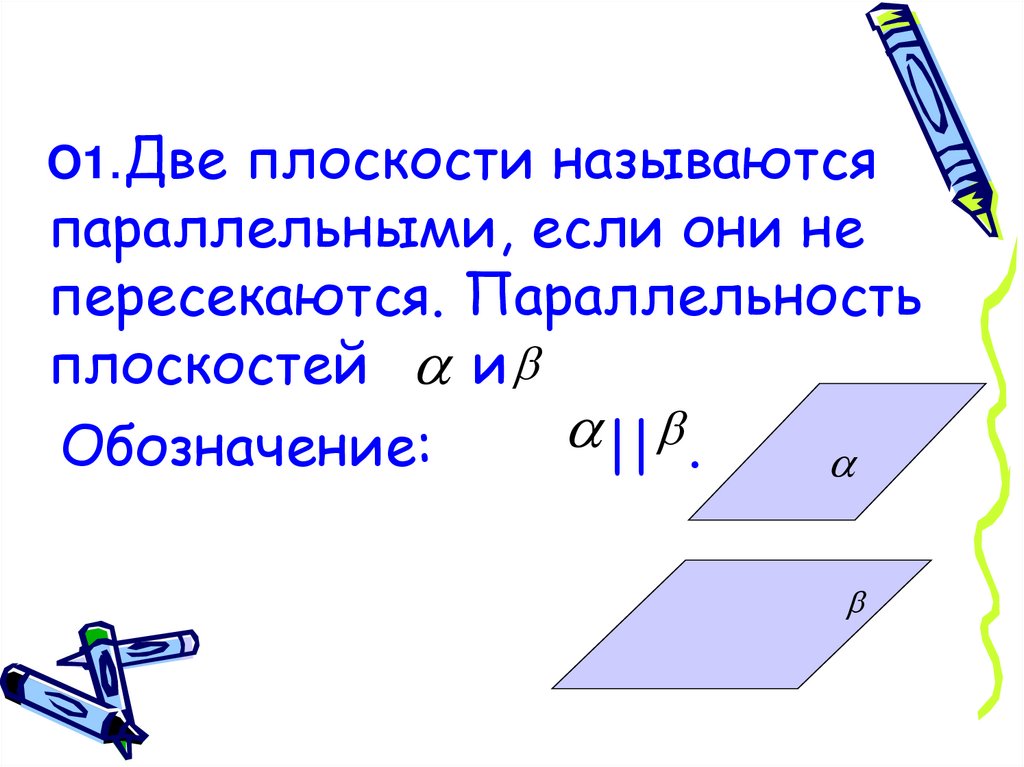
O1.Две плоскости называются
параллельными, если они не
пересекаются. Параллельность
плоскостей и
|| .
Обозначение:

25.

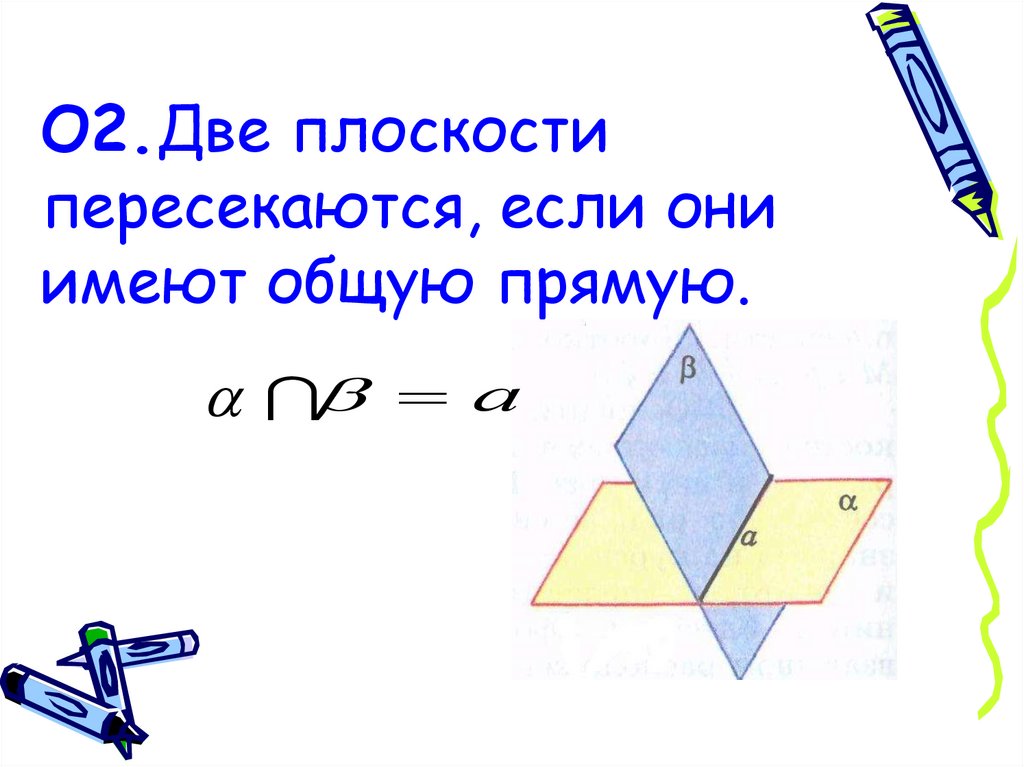
О2.Две плоскости
пересекаются, если они
имеют общую прямую.
а

26.

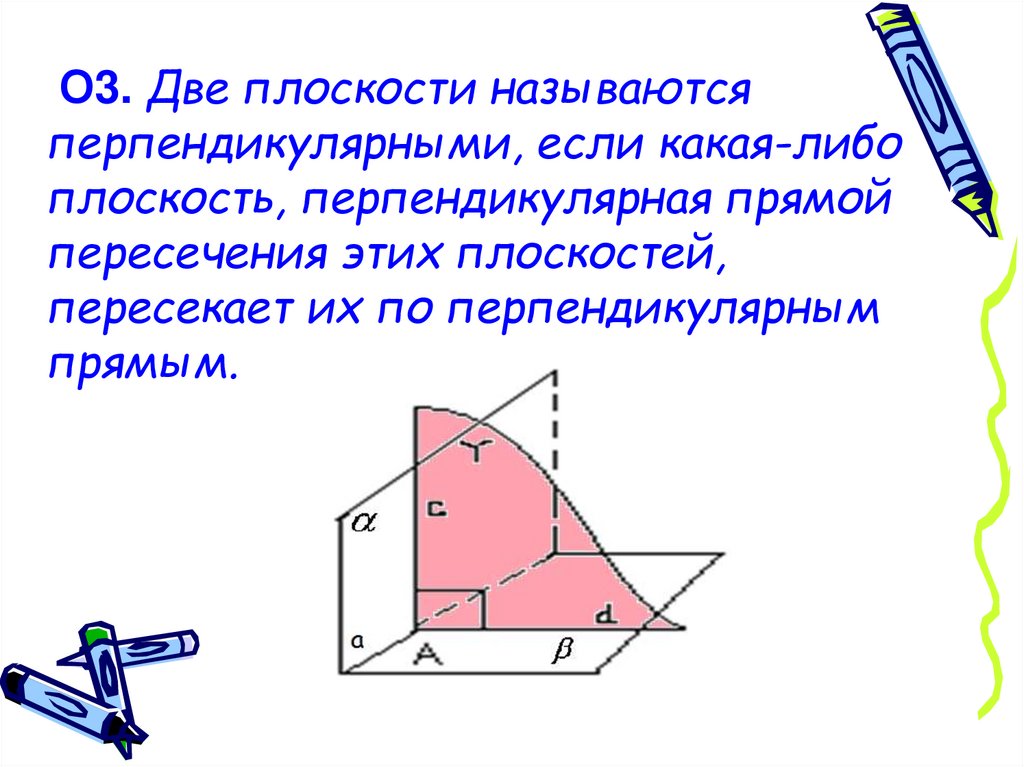
О3. Две плоскости называются
перпендикулярными, если какая-либо
плоскость, перпендикулярная прямой
пересечения этих плоскостей,
пересекает их по перпендикулярным
прямым.

27. Признак параллельности двух плоскостей

Если две пересекающиеся
прямые одной плоскости
соответственно
параллельны двум
пересекающимся прямым
другой плоскости, то эти
плоскости параллельны.

28. Признак перпендикулярности плоскостей

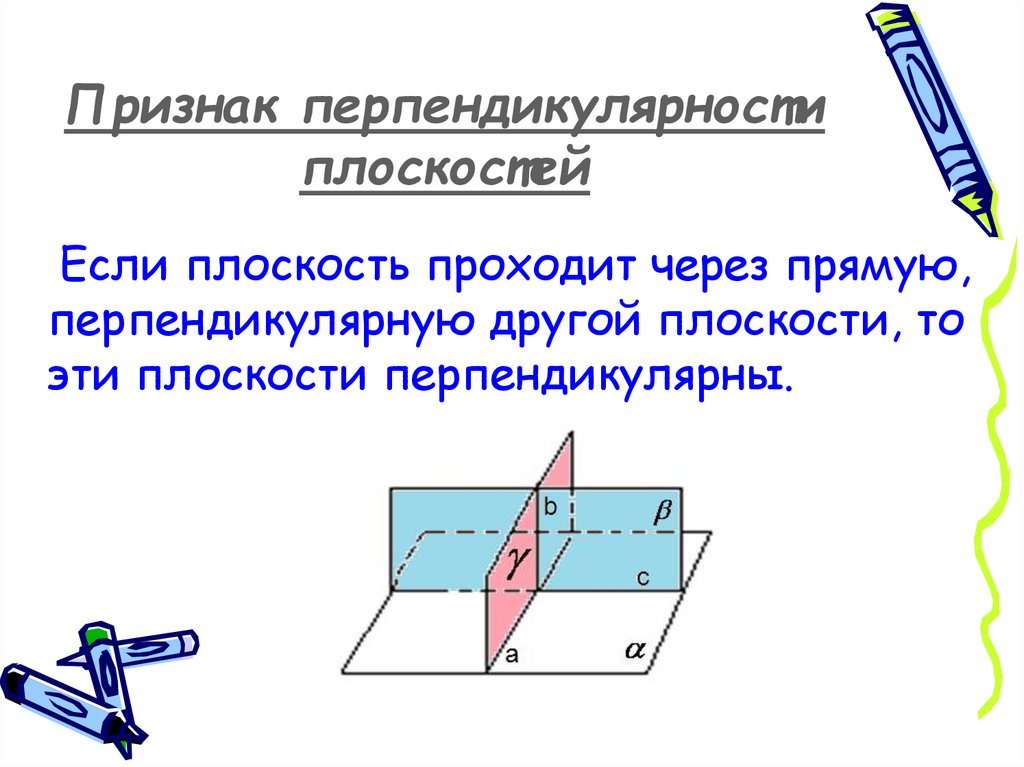
Если плоскость проходит через прямую,
перпендикулярную другой плоскости, то
эти плоскости перпендикулярны.