Множество[1]

1.

Множество.
Операции над
множествами.
Выполнила студентка группы 1НИ Шмонова Елена
Федоровна

2.

Георг Кантор (1845-1918 гг.) - немецкий математик,
основоположенник теории о множествах
«Множество есть
много, мыслимое
нами как единое»

3.

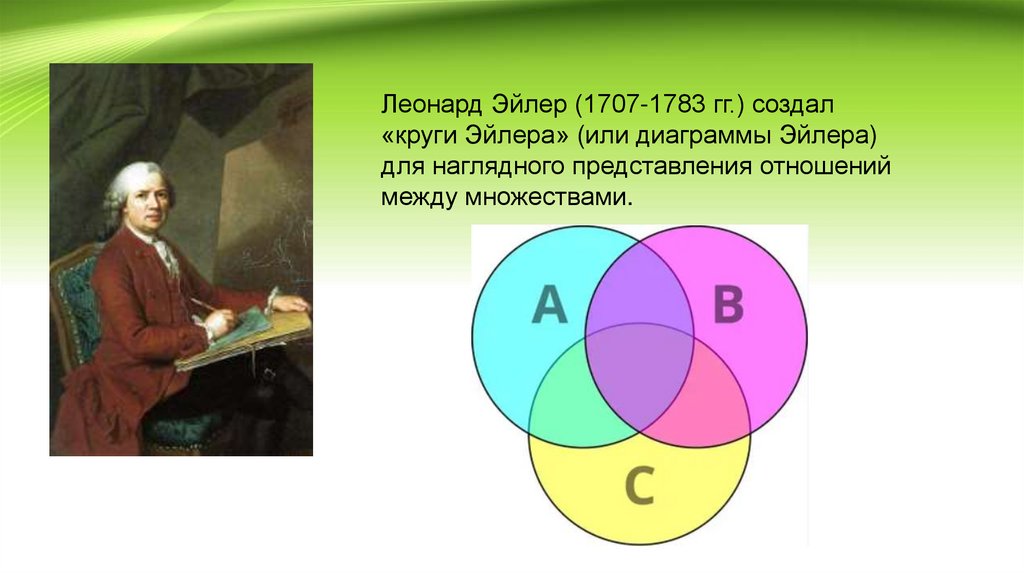
Леонард Эйлер (1707-1783 гг.) создал
«круги Эйлера» (или диаграммы Эйлера)
для наглядного представления отношений
между множествами.

4.

Множество - это простейшее математическое понятие,
оно не определяется, но поясняется как совокупность
каких-либо объектов.
Множеством является совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.
Множество «Мороженное»
Множество «Игрушки»

5.

Множества делятся на конечные и бесконечные.
Конечные множества
Бесконечные множества

6.

Объекты, из которых образовано множество,
называются элементами множества.
Множество «Транспорт»:
-Элемент
множества
«Транспорт»
-Элемент
множества
«Транспорт»
-Элемент
множества
«Транспорт»
-Элемент
множества
«Транспорт»

7.

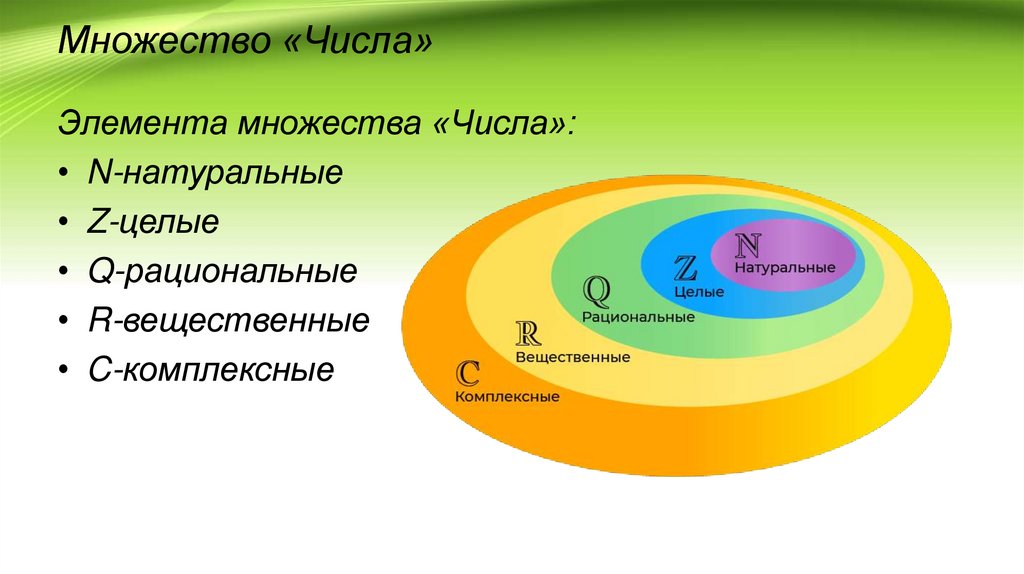
Множество «Числа»
Элемента множества «Числа»:
• N-натуральные
• Z-целые
• Q-рациональные
• R-вещественные
• C-комплексные

8.

Способы задания множеств
Множество можно задать:
1) Перечислив все его элементы:
А= 1,2,3,4,5,6,7,8,9
В= лилия, пион, роза, гортензия
2) Указать характеристическое свойство его
элементов: множество НЕЧЕТНЫХ чисел: свойство,
характеризующее каждый элементданного
множества,-ДЕЛЕНИЕ НА 2 ПРИВОДИТ К ЧАСТНОМУ
С ОСТАТКОМ.

9.

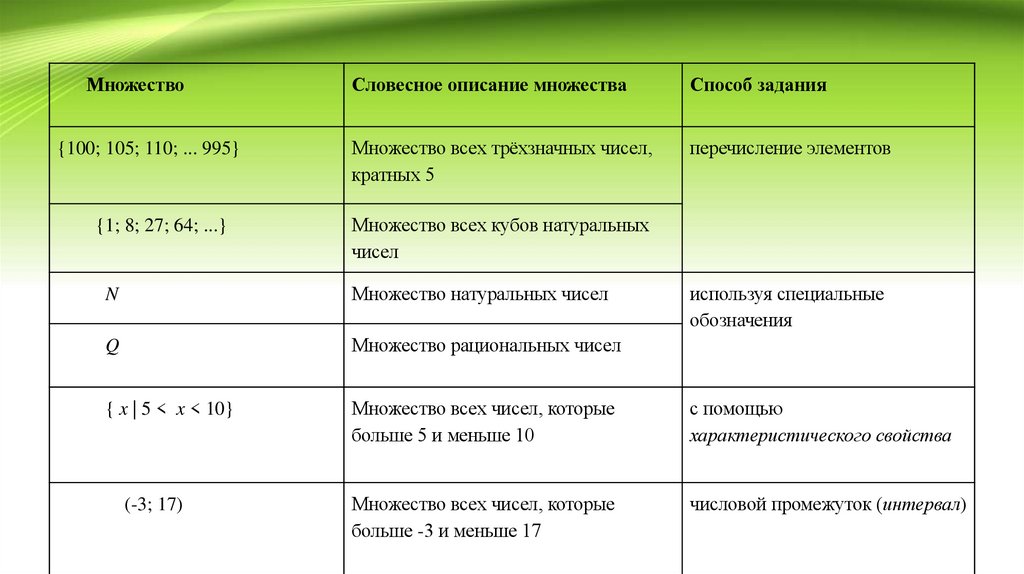
Множество
Словесное описание множества
Способ задания
{100; 105; 110; ... 995}
Множество всех трёхзначных чисел,
кратных 5
перечисление элементов
{1; 8; 27; 64; ...}
Множество всех кубов натуральных
чисел
N
Множество натуральных чисел
Q
Множество рациональных чисел
{ x | 5 < x < 10}
Множество всех чисел, которые
больше 5 и меньше 10
с помощью
характеристического свойства
Множество всех чисел, которые
больше -3 и меньше 17
числовой промежуток (интервал)
(-3; 17)
используя специальные
обозначения

10.

Подмножество - это часть более крупного
множества, состоящее только из элементов,
принадлежащих к исходному множеству.
Множество «Фруктовая тарелка»
Подмножества:
-Апельсин
-Малина
-Виноград
Пусть множество «Фруктовая
тарелка»=А, подмножество
«Апельсин»=В, тогда В⸦А, то есть
подмножество «Апельсин» включено в
множество «Фруктовая тарелка»
В⸦А Знак ⸦называется включением

11.

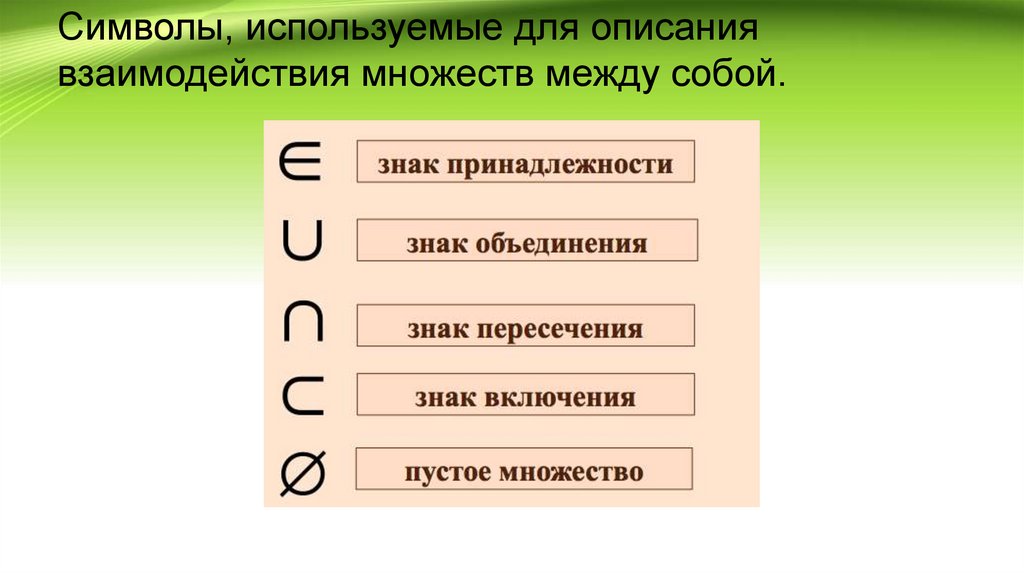
Символы, используемые для описания
взаимодействия множеств между собой.

12.

Операции над множествами.
Объединением двух множеств называется множество,
состящее из элементов, которые принадлежат хотя бы
одному из данных множеств.
Пример: А= 12,3 ;В= 4,5,6 , тогда А В 1,2,3,4,5,6
=

13.

Операции над множествами.
Пересечением множеств А и В называют множество,
состоящее из всех общих элементов множеств А и В, т.
е. из всех элементов, которые принадлежат и
множеству А и множеству В.
=
Множество «Два рыжик кота» пересекается с множеством «Рыжий кот и
серый кот» получается элементом пересечения данных множеств
является рыжий кот.

14.

Операции над множествами.
Разность двух множеств A и B — это множество,
содержащее все элементы из множества A, которые не
входят в множество B.
Множество А=все собаки;
Множество В=все собаки с ошейниками.
Тогда А\В= собаки без ошейника
\
=

15.

СПАСИБО ЗА ВНИМАНИЕ!