DG_cv_7_Ax

1.

http://www.math.sk/~skripta/deskriptivna-geometria-pre-stavebne-odbory/
2

2.

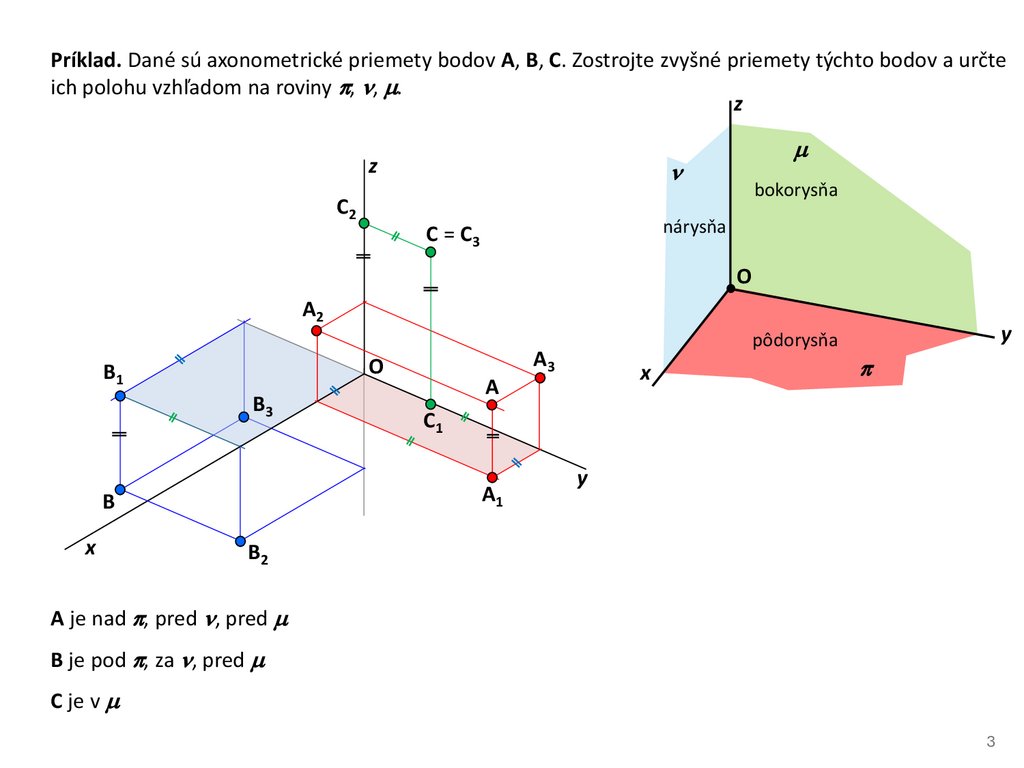
Príklad. Dané sú axonometrické priemety bodov A, B, C. Zostrojte zvyšné priemety týchto bodov a určte
ich polohu vzhľadom na roviny , , .
z
z
C2
bokorysňa
nárysňa
C = C3
O
A2
B3
x
A
C1
A1
B
x
A3
O
B1
y
pôdorysňa
y
B2
A je nad , pred , pred
B je pod , za , pred
C je v
3

3.

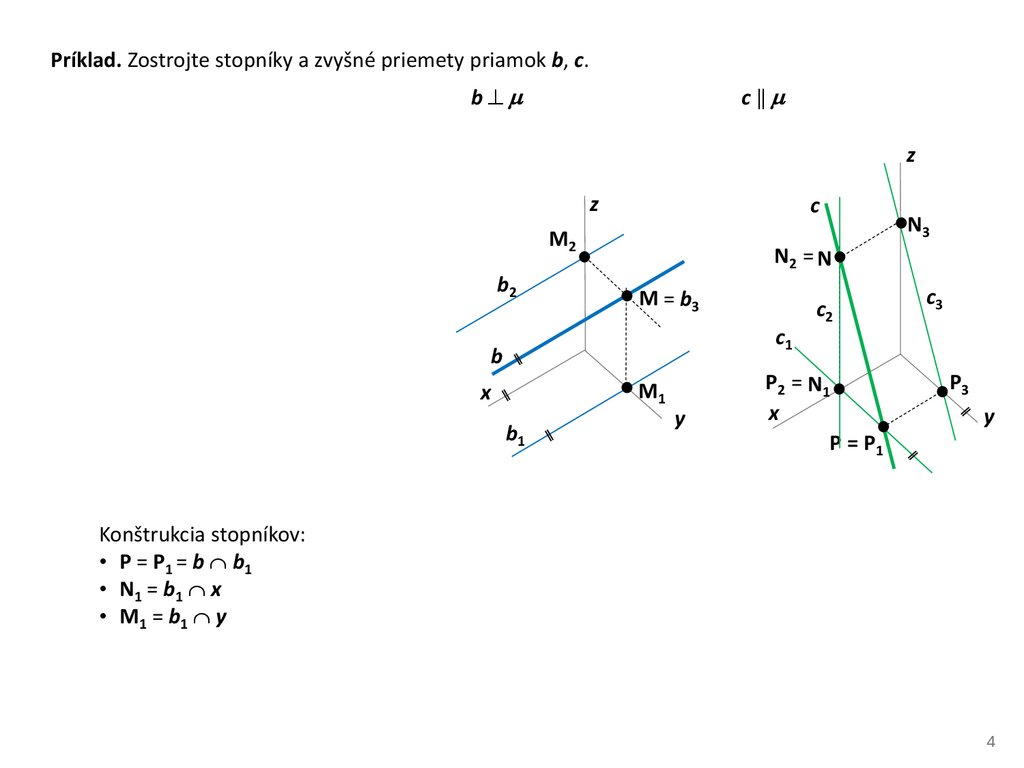
Príklad. Zostrojte stopníky a zvyšné priemety priamok b, c.
b⊥
c
z
z
c
M2
b2
N3
N2 = N
M = b3
c2
c3
c1
b
M1
x
b1
y
P2 = N 1
x
P = P1
P3
y
Konštrukcia stopníkov:
• P = P1 = b b1
• N1 = b1 x
• M1 = b1 y
4

4.

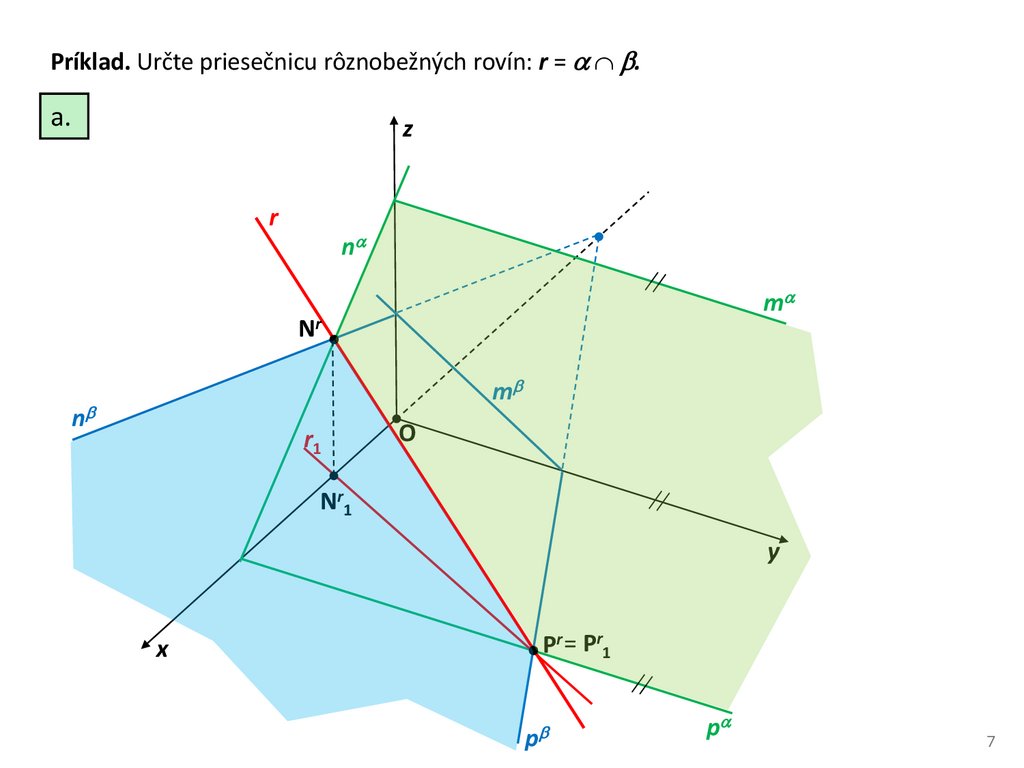
Príklad. Určte priesečnicu rôznobežných rovín: r = .
a.
z
r
n
m
Nr
m
n
r1
O
Nr1
y
x
Pr = Pr1
p
p
7

5.

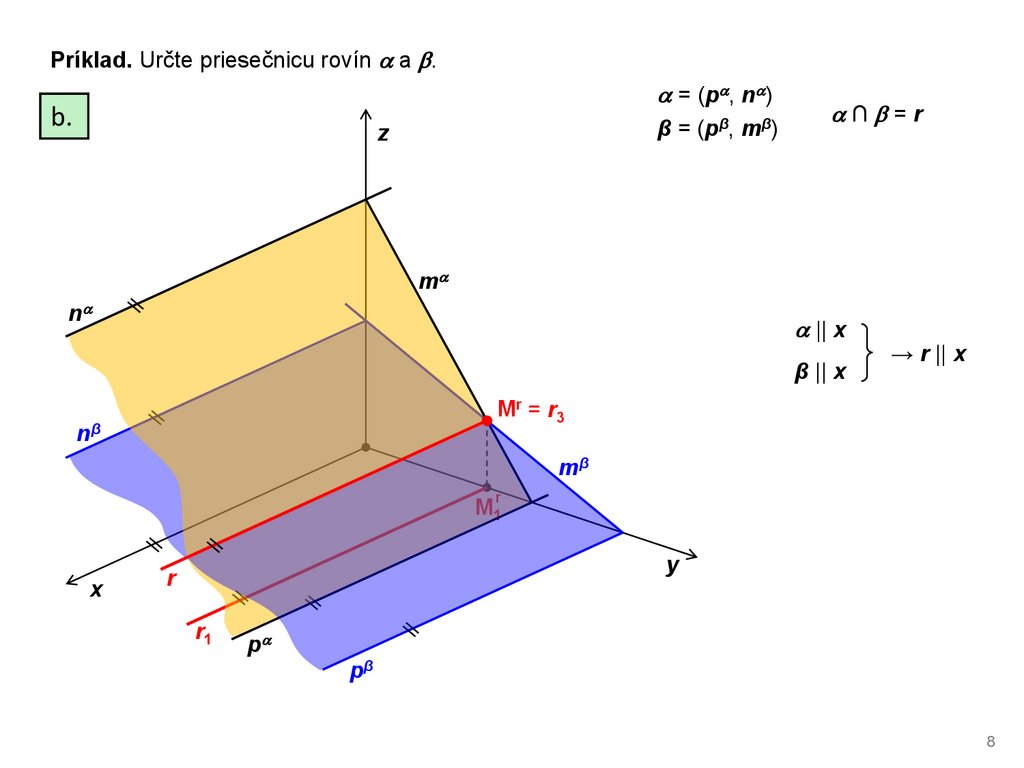
Príklad. Určte priesečnicu rovín a .
= (p , n )
b.
β = (pβ, mβ)
z
∩ =r
m
n
|| x
β || x
→ r || x
Mr = r3
nβ
mβ
r
M1
x
y
r
r1
p
pβ
8

6.

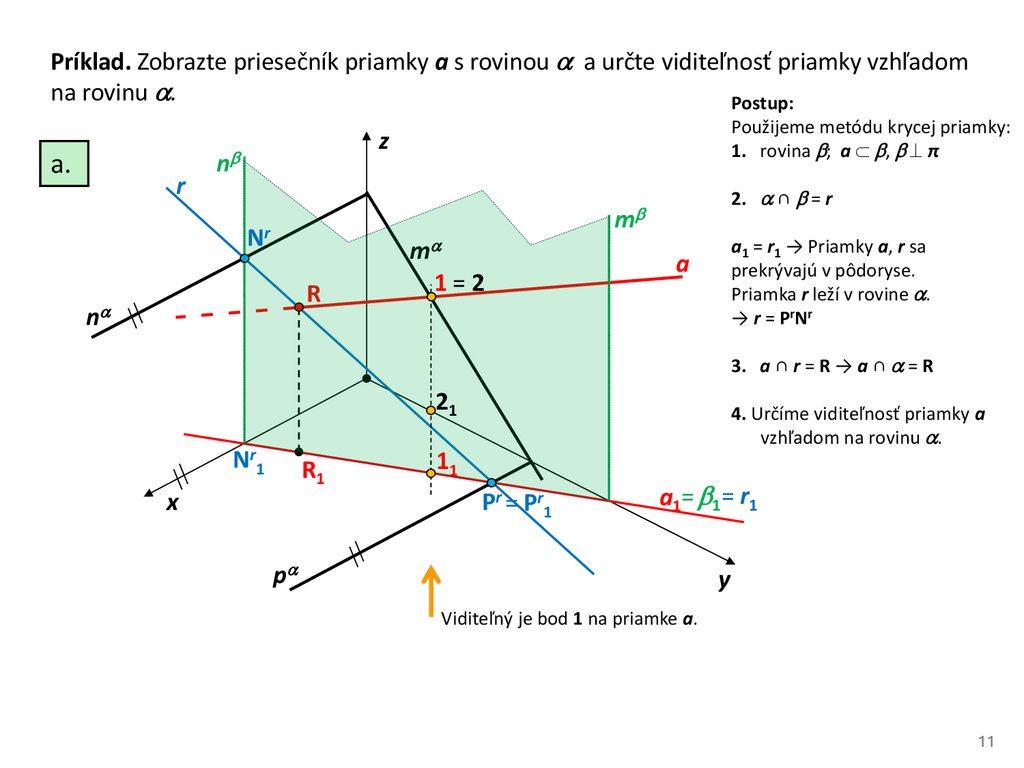
Príklad. Zobrazte priesečník priamky a s rovinou a určte viditeľnosť priamky vzhľadom
na rovinu .
Postup:
a.
r
Použijeme metódu krycej priamky:
1. rovina ; a , ⊥ π
z
n
Nr
R
n
m
1=2
2. ∩ = r
m
a1 = r1 → Priamky a, r sa
prekrývajú v pôdoryse.
Priamka r leží v rovine .
→ r = PrNr
a
3. a ∩ r = R → a ∩ = R
21
Nr1
R1
4. Určíme viditeľnosť priamky a
vzhľadom na rovinu .
11
Pr = Pr1
x
a1= 1 = r1
p
y
Viditeľný je bod 1 na priamke a.
11

7.

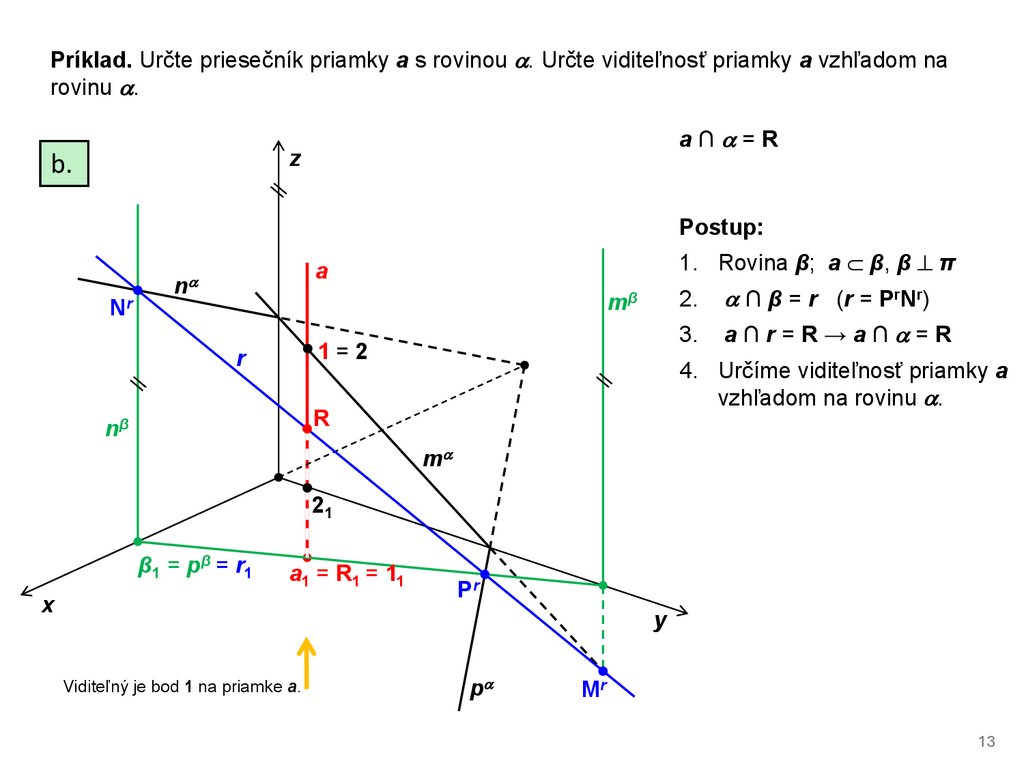
Príklad. Určte priesečník priamky a s rovinou . Určte viditeľnosť priamky a vzhľadom na
rovinu .
a∩ =R
z
b.
Postup:
Nr
1. Rovina β; a β, β ⊥ π
a
n
2.
mβ
3.
1=2
r
4. Určíme viditeľnosť priamky a
vzhľadom na rovinu .
R
nβ
∩ β = r (r = PrNr)
a∩r=R→a∩ =R
m
21
β1 = pβ = r1
a1 = R1 = 11
x
Pr
y
Viditeľný je bod 1 na priamke a.
p
Mr
13

8.

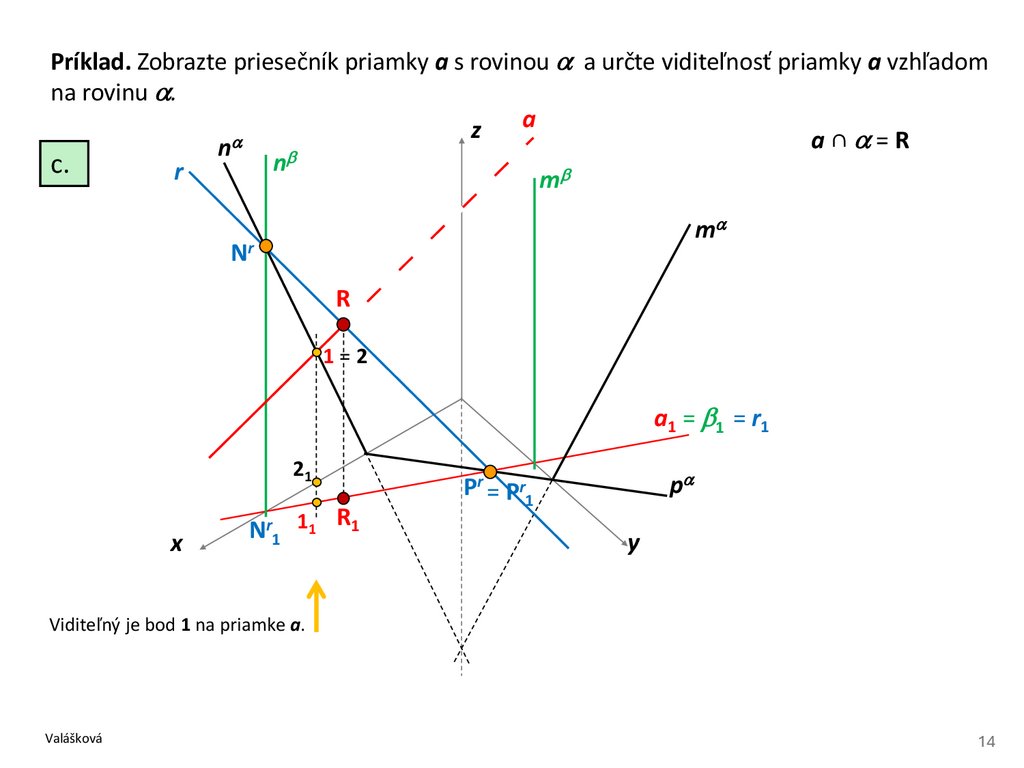
Príklad. Zobrazte priesečník priamky a s rovinou a určte viditeľnosť priamky a vzhľadom
na rovinu .
a
z
a∩ =R
n
n
c.
r
m
m
Nr
R
1=2
a1 = 1 = r1
21
x
Nr1 11
R1
p
Pr = Pr1
y
Viditeľný je bod 1 na priamke a.
Valášková
14

9.

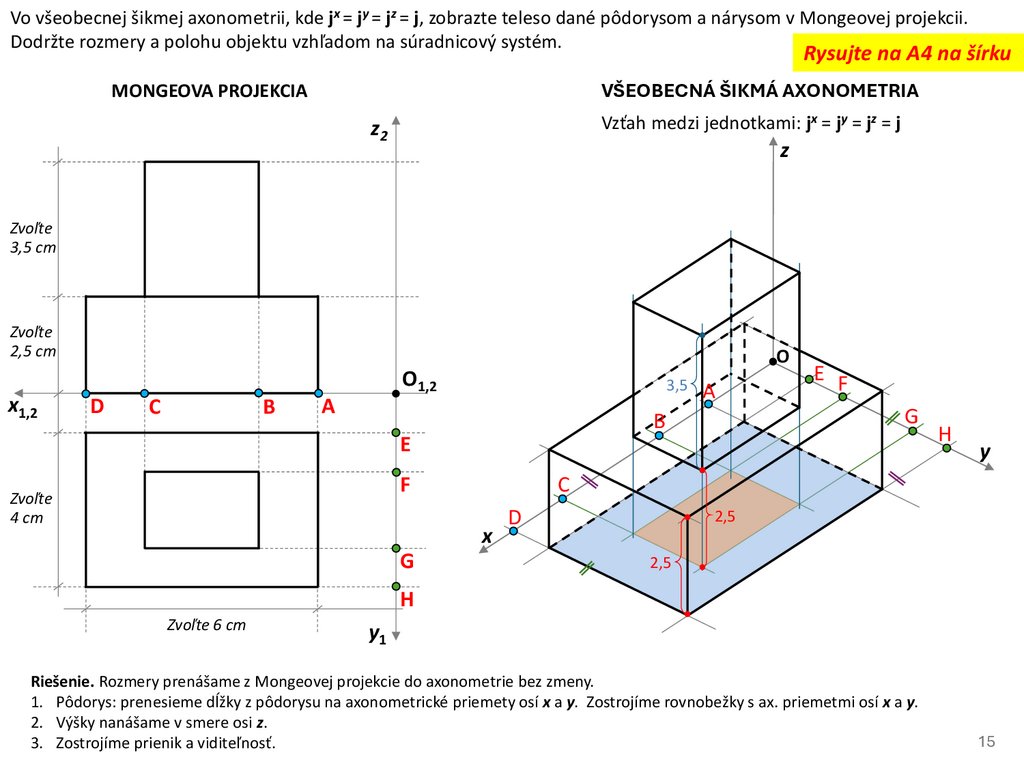
Vo všeobecnej šikmej axonometrii, kde jx = jy = jz = j, zobrazte teleso dané pôdorysom a nárysom v Mongeovej projekcii.
Dodržte rozmery a polohu objektu vzhľadom na súradnicový systém.
Rysujte na A4 na šírku
VŠEOBECNÁ ŠIKMÁ AXONOMETRIA
MONGEOVA PROJEKCIA
Vzťah medzi jednotkami: jx = jy = jz = j
z2
z
Zvoľte
3,5 cm
Zvoľte
2,5 cm
O
O1,2
x1,2
D
C
B
3,5
A
A
E F
G
B
E
x
G
y
C
F
Zvoľte
4 cm
H
D
2,5
2,5
H
Zvoľte 6 cm
y1
Riešenie. Rozmery prenášame z Mongeovej projekcie do axonometrie bez zmeny.
1. Pôdorys: prenesieme dĺžky z pôdorysu na axonometrické priemety osí x a y. Zostrojíme rovnobežky s ax. priemetmi osí x a y.
2. Výšky nanášame v smere osi z.
3. Zostrojíme prienik a viditeľnosť.
15