Лекция 5 Множества

1. Множества и основные операции над ними.

Общие понятия теории множеств. Способы
задания. Основные операции над множествами
и их свойства. Мощность множеств.
Графическое изображение множеств на
диаграммах Эйлера-Венна. Декартово
произведение множеств.

2. Понятие множества

Множество - это соединение в одно целое
каких-либо объектов.
Объекты, составляющие множество,
называют элементами. Все элементы
множества отличаются друг от друга.
Порядок элементов в множестве не имеет
значения.

3. Обозначения

m S , m S
Множество, содержащее конечное число
элементов, называется конечным. Если же
множество не содержит ни одного
элемента, то оно называется пустым и
обозначается .

4. Подмножество

Множество M называется подмножеством
множества S (обозначение М S либо S М;
читается М входит в S, S содержит М) тогда
и только тогда, когда любой элемент
множества М принадлежит множеству S.
Например: S – множество
натуральных чисел,
М – множество четных чисел.
М S

5. Мощность множества

Число элементов конечного множества S
называется его мощностью и обозначается
|S|.
Два множества называются равными, если
эти множества содержат одинаковые
элементы
Универсальное множество (универсум) U,
содержащее все элементы, которые нас
интересуют

6. Способы задания множеств

1. Перечисление элементов
A = {1, 2, 4, 8}
2. Порождающая процедура
3. Описание свойств его элементов
M={x | x 2 3x 2 0 }

7. Операции над множествами

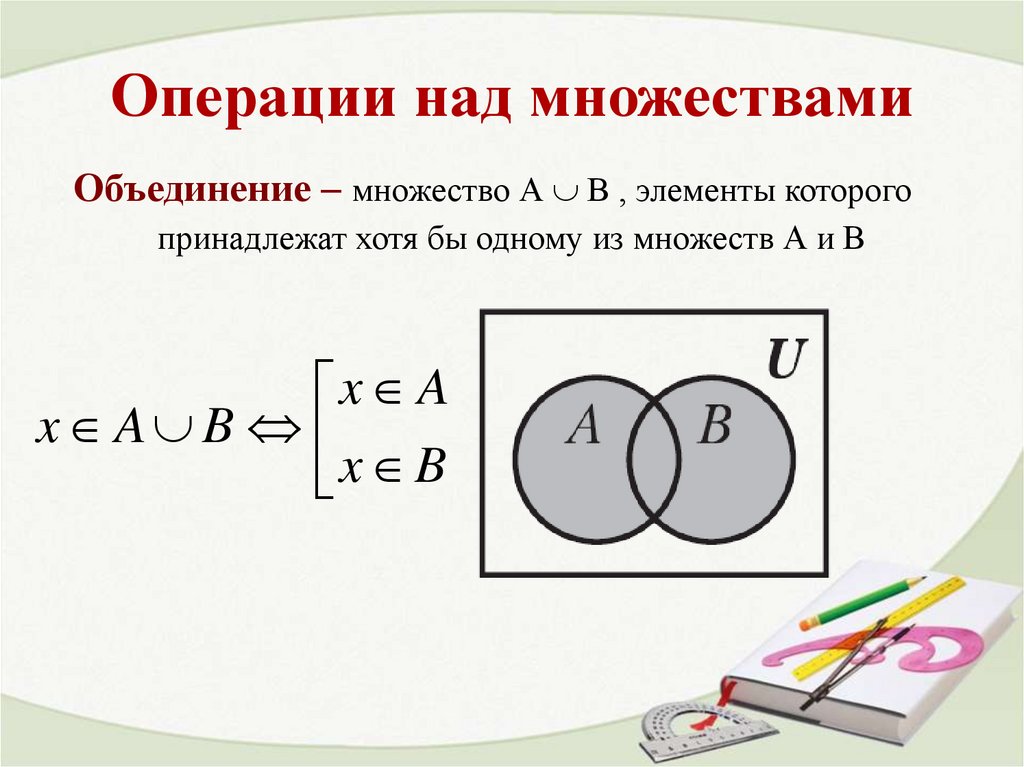
Объединение – множество А В , элементы которого
принадлежат хотя бы одному из множеств А и В
x A
x A B
x B

8. Операции над множествами

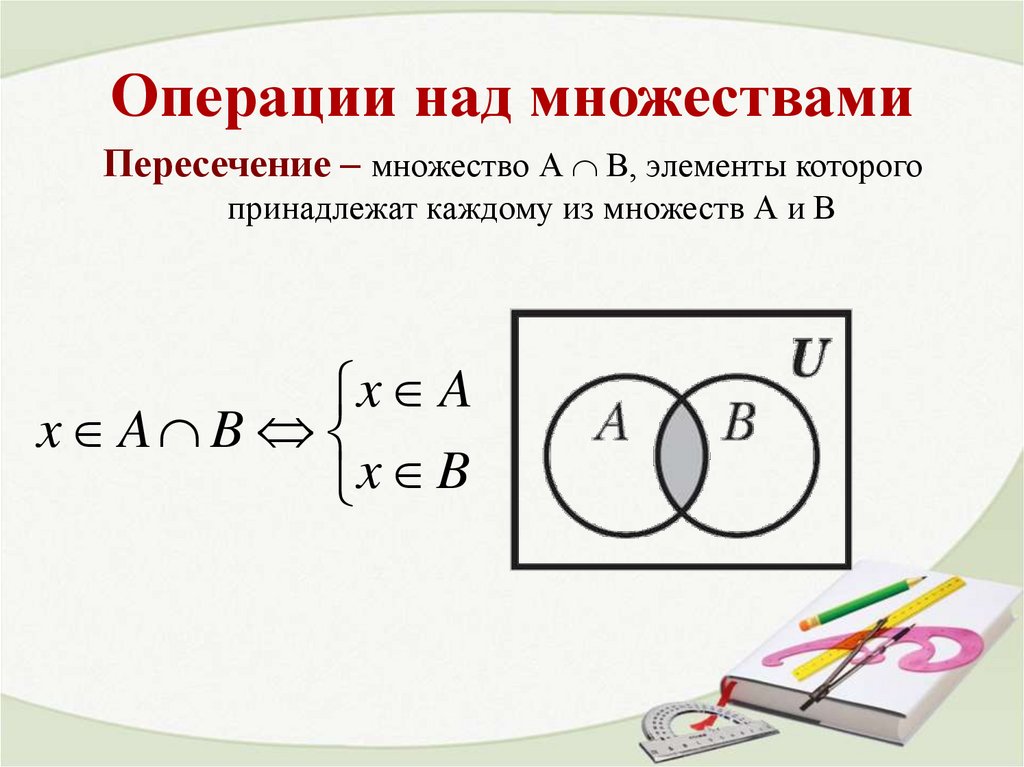
Пересечение – множество А В, элементы которого
принадлежат каждому из множеств А и В
x A
x A B
x B

9. Операции над множествами

Разность – множество А \ В , элементы которого
принадлежат множеству А, но не принадлежат множеству В
x A
x A\ B
x B

10. Операции над множествами

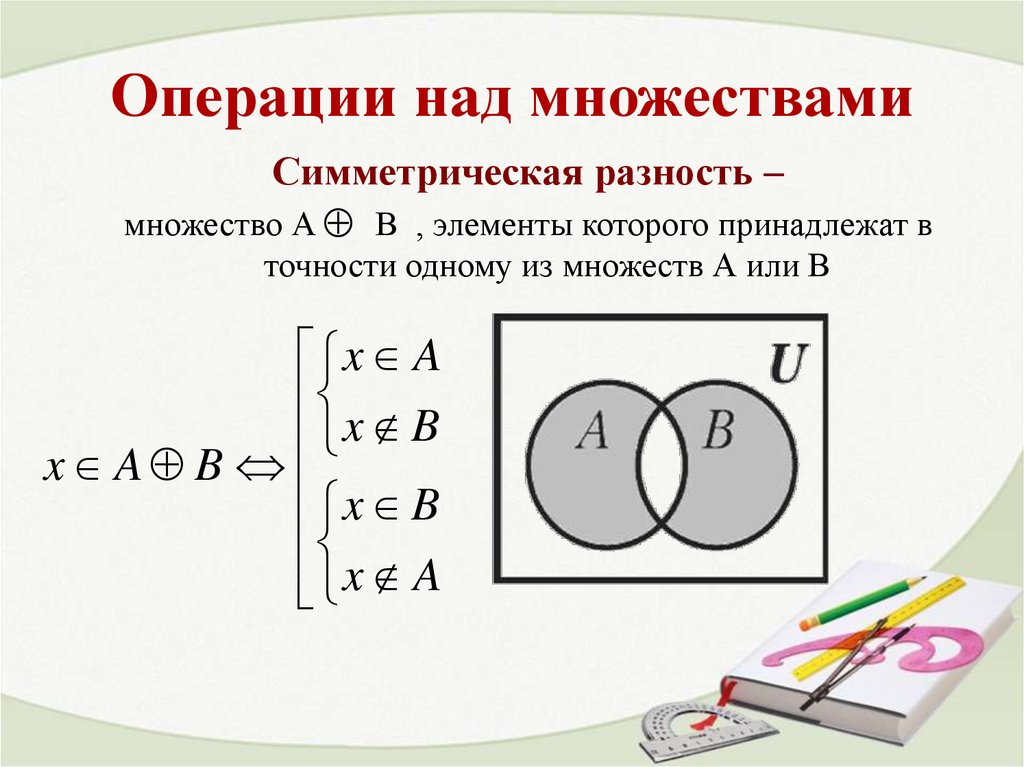
Симметрическая разность –
множество А В , элементы которого принадлежат в
точности одному из множеств А или В
x A
x B
x A B
x B
x A

11. Операции над множествами

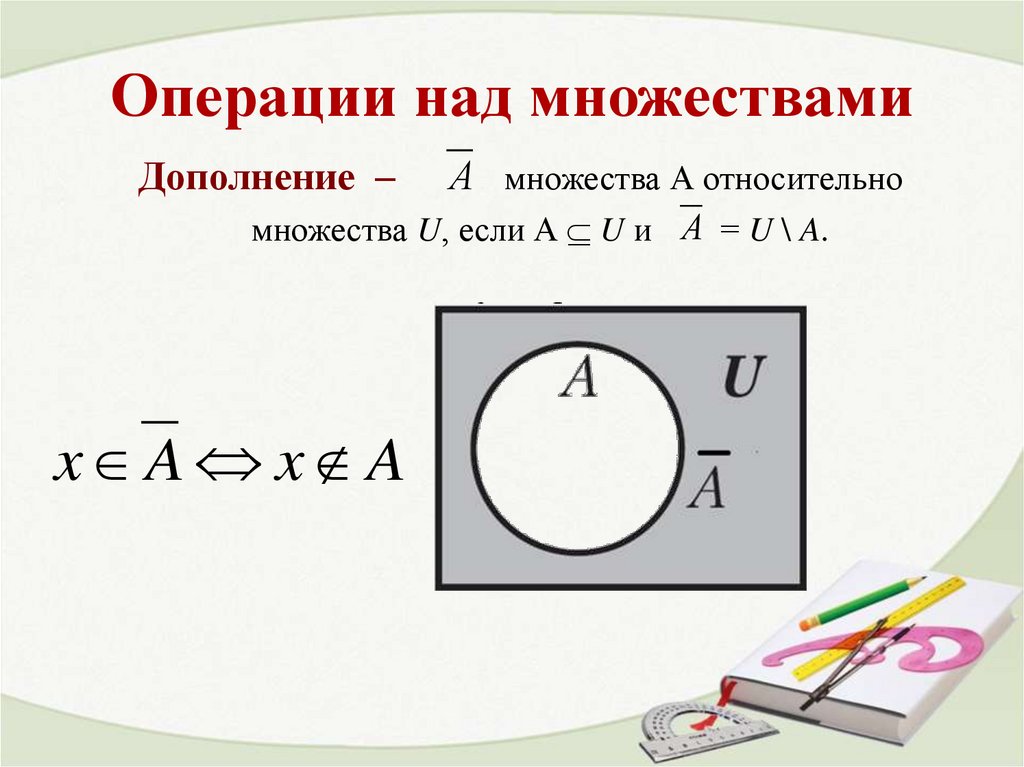
Дополнение –
А множества А относительно
множества U, если А U и А = U \ A.
x A x A

12. Свойства операций над множествами

1. А А = А А = А;
2. A B = B A; A B = B A;
3. (A B) C = A (B C); (A B) C =
A (B C);
4. A (B C) = (A B) (A C); A (B
C) = (A B) (A C);
5. A (A B) = A; A (A B) = A;
6. = А; A = ;

13. Свойства операций над множествами

14. Соответствие теоретико-множественных операций логическим операциям

15. Декартово произведение

А В – множество пар (a;b), таких, что а А,
b B.

16.

Пример №1. Проверить равенство двух
множеств тремя способами:
а) по определению
б) диаграммами Эйлера-Венна
в) с помощью формул алгебры логики
A \ (B C) = (A \ B) (A \ C).

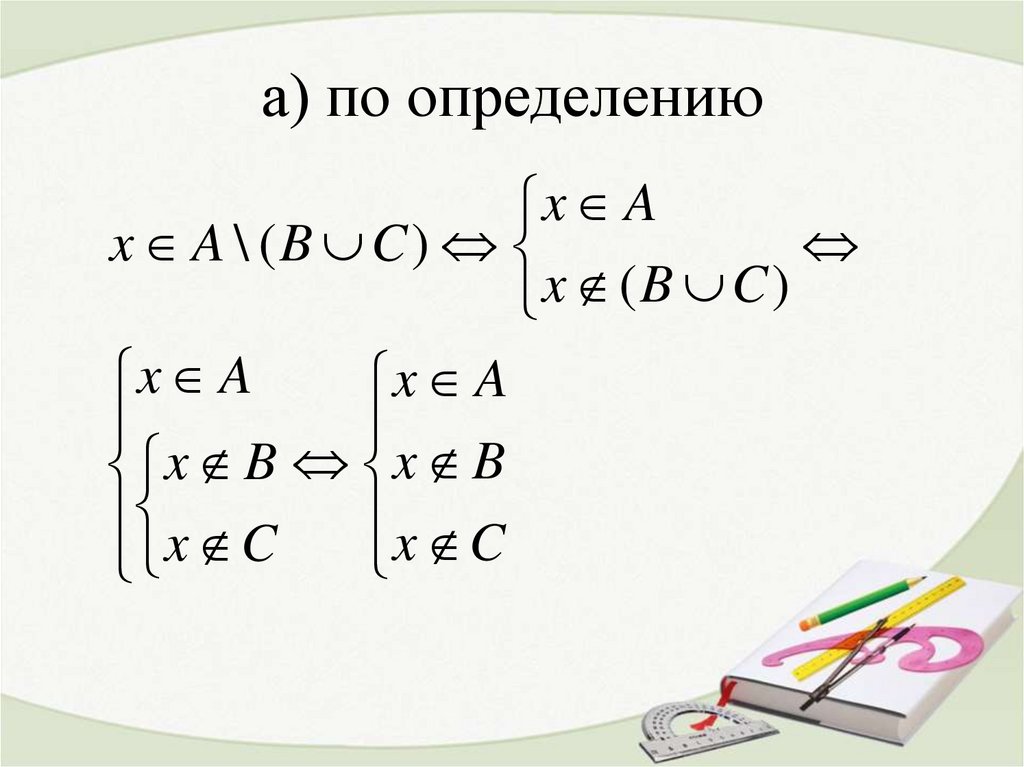
17. а) по определению

x A
x A \ (B C)
x (B C)
x A
x A
x B x B
x C
x C

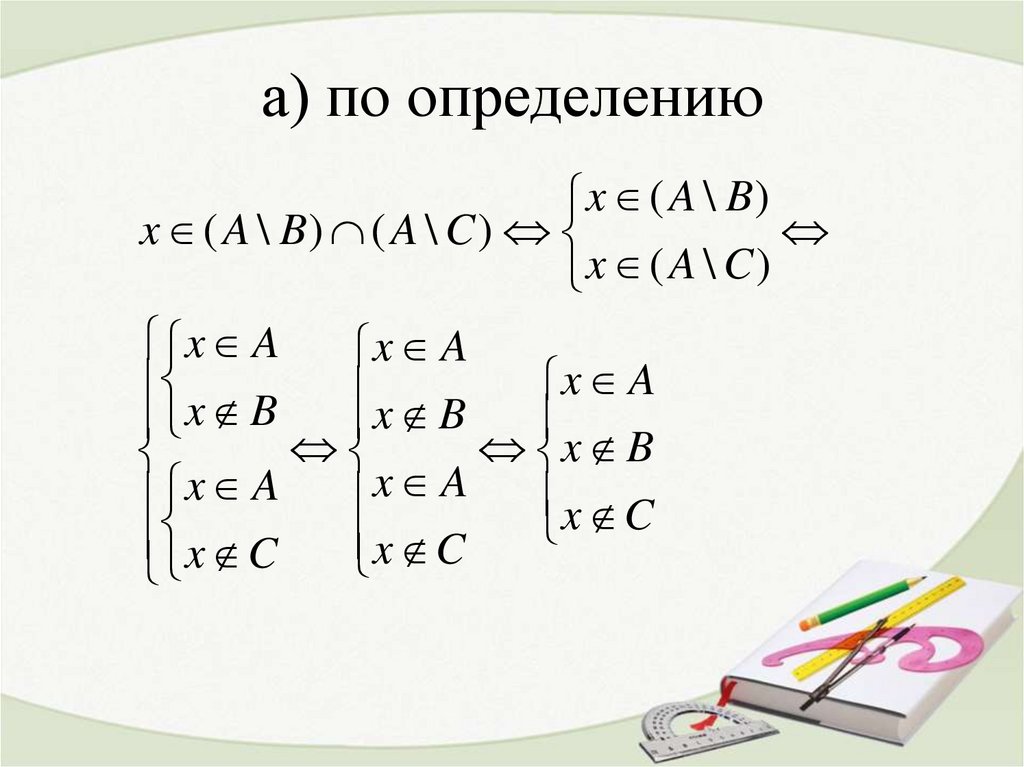
18. а) по определению

x ( A \ B)
x ( A \ B) ( A \ C )
x ( A \ C)
x A
x A
x A
x B
x B
x B
x A
x A
x C
x C
x C

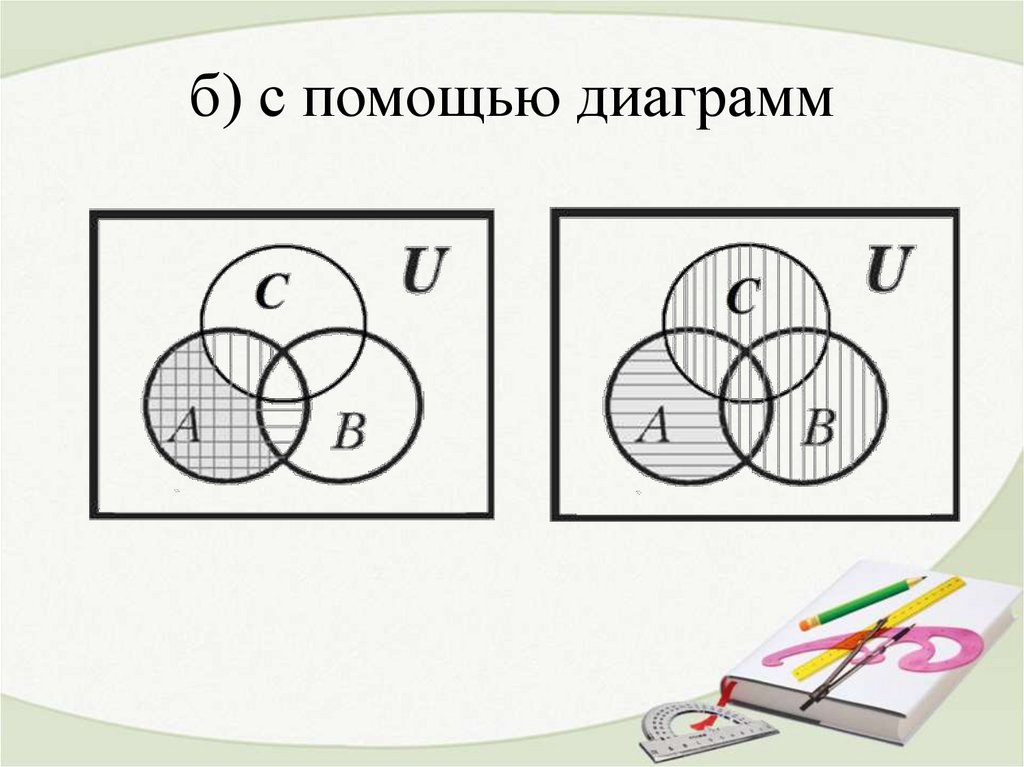
19. б) с помощью диаграмм

20. в) по аналогии с АЛ

A \ B C A B C
A B C A B C
A \ B A \ C A B A C
A B A C A B C

21.

Пример №2. Заданы подмножества A, B и C
множества арабских цифр. Найдите
подмножества D A B C , E A \ B C .
A 1,4,6,8,9 B 0,3,5,6,9 C 2,4,6,8,9
Решение.
B C 0,2,3,4,5,6,8,9
A B C 4,6,8,9
A \ B 1,5,8
C 0,1,3,5,7
A \ B C 1,5