Презентация к уроку вероятности и статистики _Свойства операций над множествами_ пере

1. Свойства операций над множествами: переместительное, сочетательное, распределительное, включения.

2. Объединение множеств

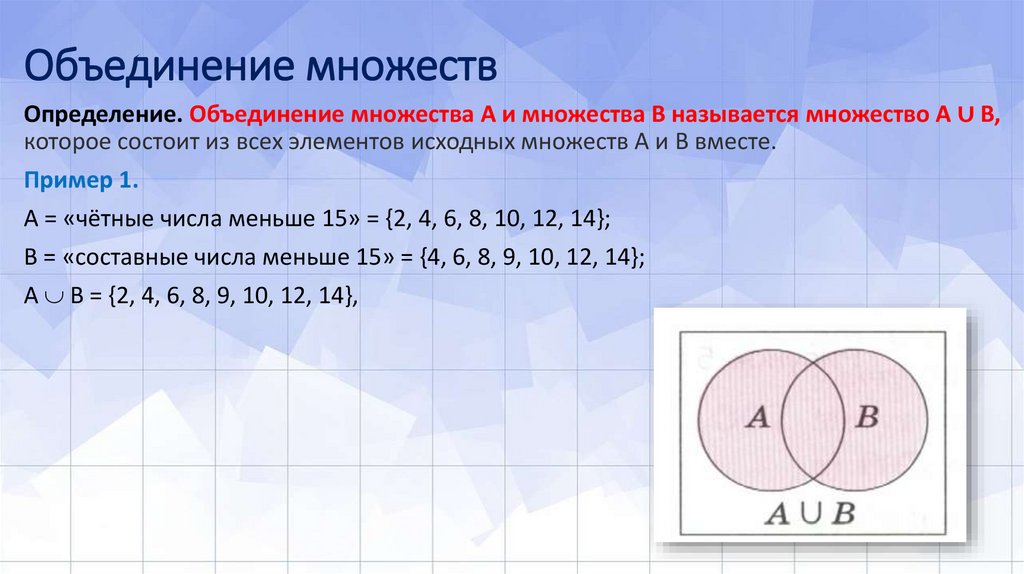
Определение. Объединение множества А и множества В называется множество A ∪ B,
которое состоит из всех элементов исходных множеств A и B вместе.
Пример 1.
А = «чётные числа меньше 15» = {2, 4, 6, 8, 10, 12, 14};
B = «составные числа меньше 15» = {4, 6, 8, 9, 10, 12, 14};
A B = {2, 4, 6, 8, 9, 10, 12, 14},

3. Пересечений событий

Определение. Пересечение A ∩ B двух множеств A и B состоит из
элементов, которые принадлежат обоим исходным множествам.
Пример 2.
А = «чётные числа меньше 15» = {2, 4, 6, 8, 10, 12, 14};
B = «составные числа меньше 15» = {4, 6, 8, 9, 10, 12, 14};
A B = {4, 6, 8, 10, 12, 14}

4. Сравнение множеств

5. Разность множеств

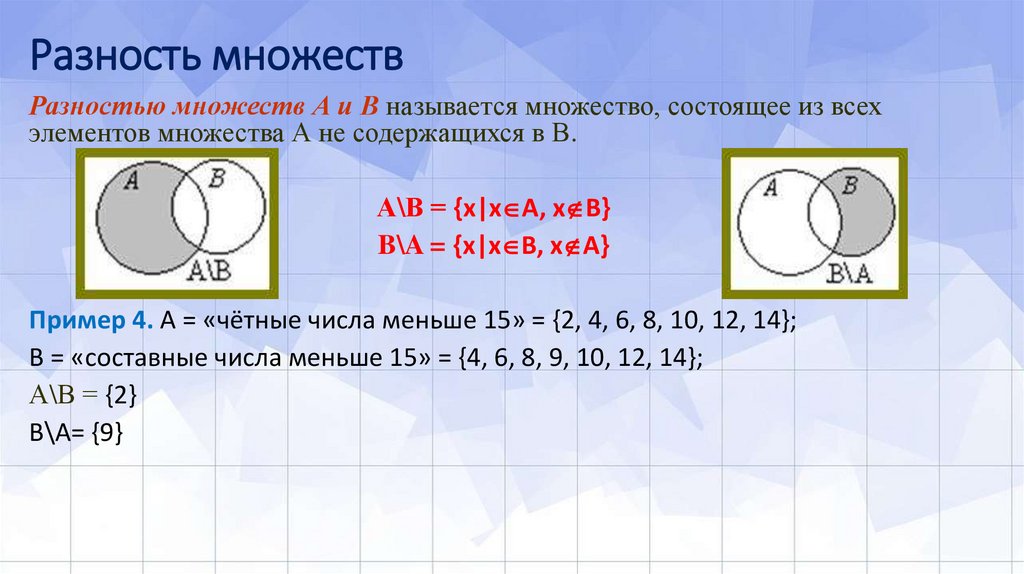
Разностью множеств А и В называется множество, состоящее из всех
элементов множества А не содержащихся в В.
А\В = {х|x A, x B}
B\A = {х|x B, x A}
Пример 4. А = «чётные числа меньше 15» = {2, 4, 6, 8, 10, 12, 14};
B = «составные числа меньше 15» = {4, 6, 8, 9, 10, 12, 14};
А\В = {2}
В\А= {9}

6. Пример 5

А={К, А, Т, Я}, В={К, О, С, Т, Я}
Найти: A B, A B , А\В, В\А и
показать решение на кругах Эйлера.
A B= {К, А, Т, Я, О, С}
A B = {К, Т, Я}
А\В = {А}
В\А= {О, С}

7. Свойства операций над множествами

8. Задание 1

На диаграмме Эйлера изображены множества А и В.
Нарисуйте диаграмму в тетради и укажите на ней
множество С, которое:
а) включает элементы множества А, а множества В нет;
б) включает элементы множества В, а множества А нет;
в) включает элементы хотя бы одного из множеств А и
В;
г) не включает в себя ни элементы множества А, ни
элементы множества В;
д) включает элементы обоих множеств.
Какое из этих множеств является множеством A B?
Какое из этих множеств является множеством A B?

9. Задание 2

Бросают одну игральную кость. Множество А – «выпадет чётное число
очков». Множество В состоит из очков:
а) кратных 3;
б) кратных 4;
в) больших 4;
г) меньших 3.
Для каждого случая выпишите элементы множеств и найдите A B, A B

10. Задание 3

В множество А входит 6 элементов, а в множество В – 8 элементов. При этом
2 элемента принадлежат одновременно обоим множествам.
Сколько элементов входит в множество:
а) С = «событие А наступает, а событие В нет»;
б) Д = «событие В наступает, а событие А нет»;
в) A B;
г) A B.

11. Домашнее задание:

1. А = множество чисел кратных 3 и меньших 20},
В = { множество чисел кратных 2 и меньших 20}.
Найдите А В, А В, А\В, В\А.
2. Найти все подмножества множества А = {0, 1, 2} и
В = {3, 5, 7, 9}.
3. На полу комнаты площадью 24 м² лежат три
ковра. Площадь одного из них 10м², другого 8 м²,
третьего 6 м². Каждые два ковра перекрываются по
площади 3 м², а площадь участка пола покрытого
всеми тремя коврами, составляет ровно 1 м².
Найдите площадь которая
а) покрыта коврами; б) покрыта 1 и 2 ковром, но не
покрыта третьим ковром; в) покрыта только первым
ковром; г) не покрыта коврами.

12. Использованные источники:

1. Математика. Вероятность и статистика. 7 – 9 классы. Базовый
уровень. Учебник в 2 – х частях. Под редакцией И.В.Ященко. –
М.: Просвещение, 2023
2. Математика. Вероятность и статистика. 10 класс. Базовый и
углубленный уровни. Учебное пособие. Под редакцией
Е.А.Бунимович, В.А.Булычев. – М.: Просвещение, 2023