Similar presentations:
вебинар_2_7_Показательная_функция,_ее_свойства_1 (3)
1.
Показательная функция, ее свойства2.
Степень с произвольнымдействительным показателем.
Определение показательной функции,
ее свойства и график. Знакомство с
применением показательной функции.
Решение показательных уравнений
функционально-графическим методом
Решение показательных уравнений
методом уравнивания показателей,
методом введения новой переменной,
функционально-графическим методом.
Решение показательных неравенств
3. Определение
Показательная функция – этоx
функция вида
,
y a
где x – переменная,
a - заданное число, a >0, a 1.
Примеры:
у 3 ;
х
х
1
у ;
2
у 0,4
х
4.
5.
• Сравнение чисел с использованием свойствпоказательной функции
• Сравнение числа с 1
а) аналитический способ;
б) графический способ.
6. Задача 1 Сравнить числа
21, 4
1
1
и
3
3
Решение
1
3
2 1,41... 1,4
1
0 1
3
Ответ:
1
3
2
1, 4
1
3
2
1, 4
1
3
7. Задача 2 Сравнить число с 1.
Задача 25
Сравнить число3 с 1.
Решение
1 3
0
-5 < 0
5
3 3
3 1
Ответ: 3 5 1
0
5
3 1
8.
Областьопределения показательной
функции: D (y)=R – множество
всех действительных чисел.
Область
значений показательной
функции: E (y)=R+ - множество
всех положительных чисел.
9.
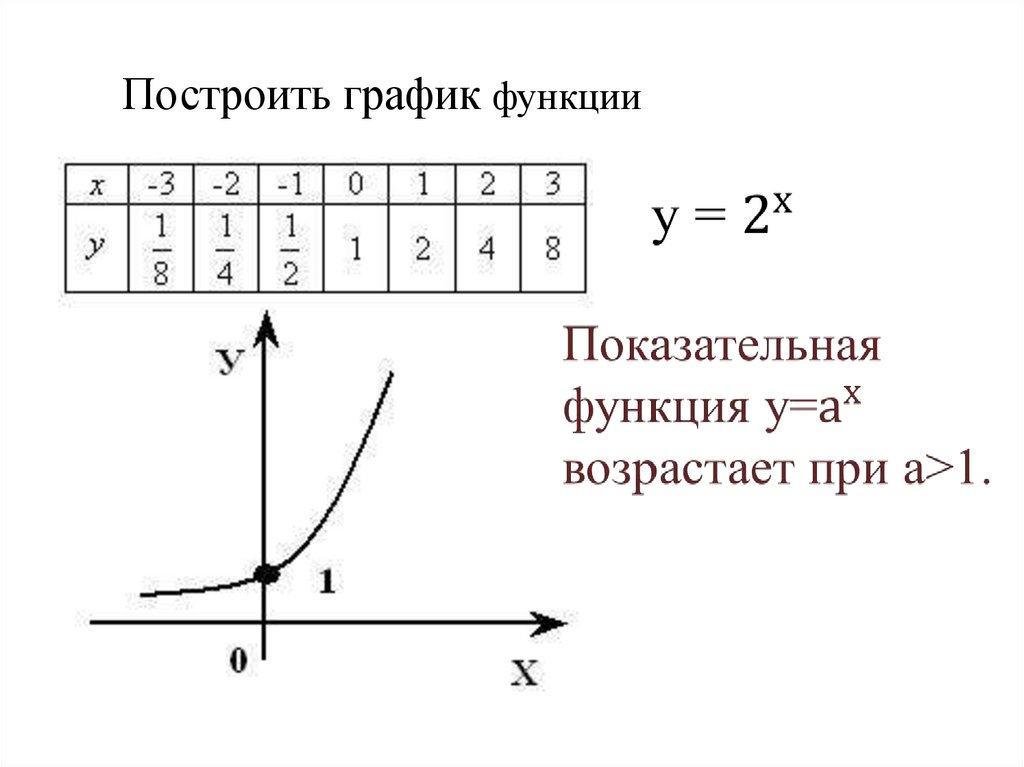
Построить график функции10.
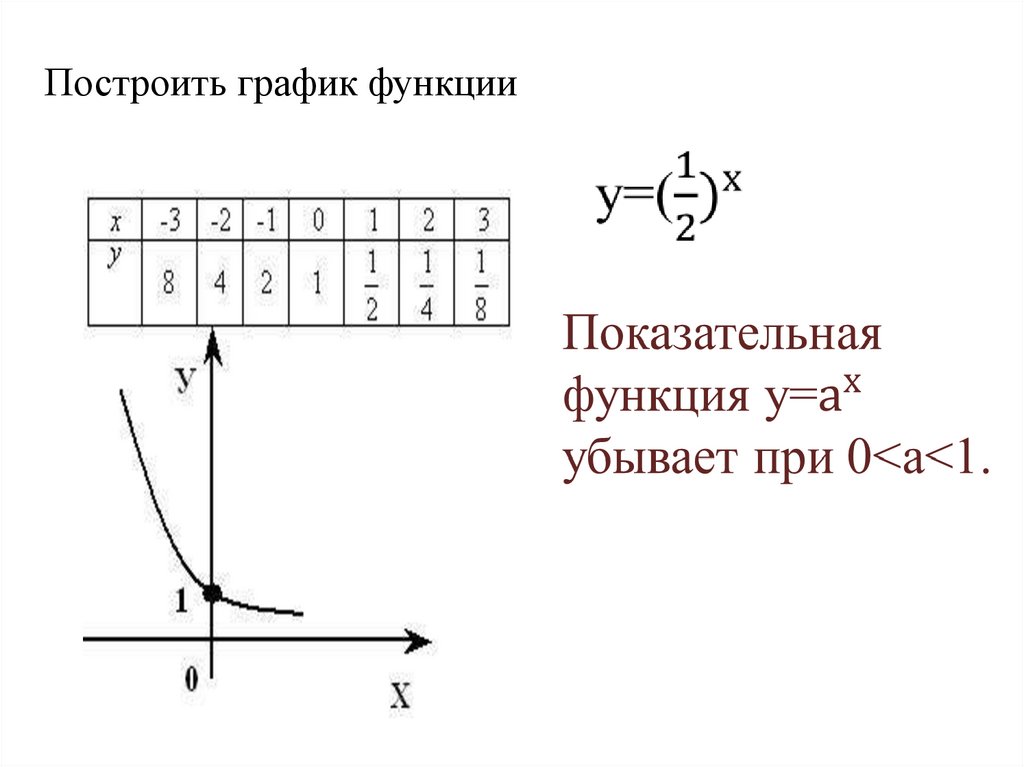
Построить график функции11.
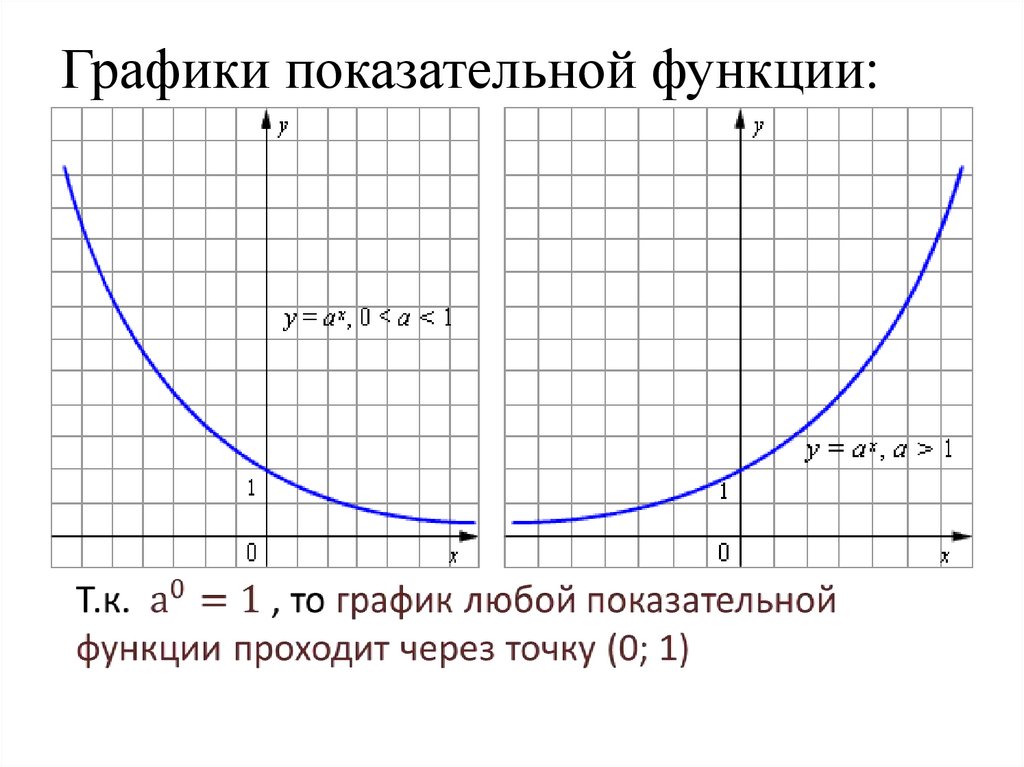
Графики показательной функции:12. Показательная функция обладает следующими свойствами:
1.2.
3.
4.
5.
6.
7.
8.
D(f): множество R всех действительных чисел;
E(f): множество всех положительных чисел;
f(x)>0 при любом значении х;
Показательная функция у=ах является возрастающей на
множестве всех действительных чисел, если а>1,и
убывающей, если 0<а<1;
Не является ни четной, ни нечетной;
Не ограничена сверху, ограничена снизу;
Не имеет ни наибольшего, ни наименьшего значения;
Непрерывна.
13.
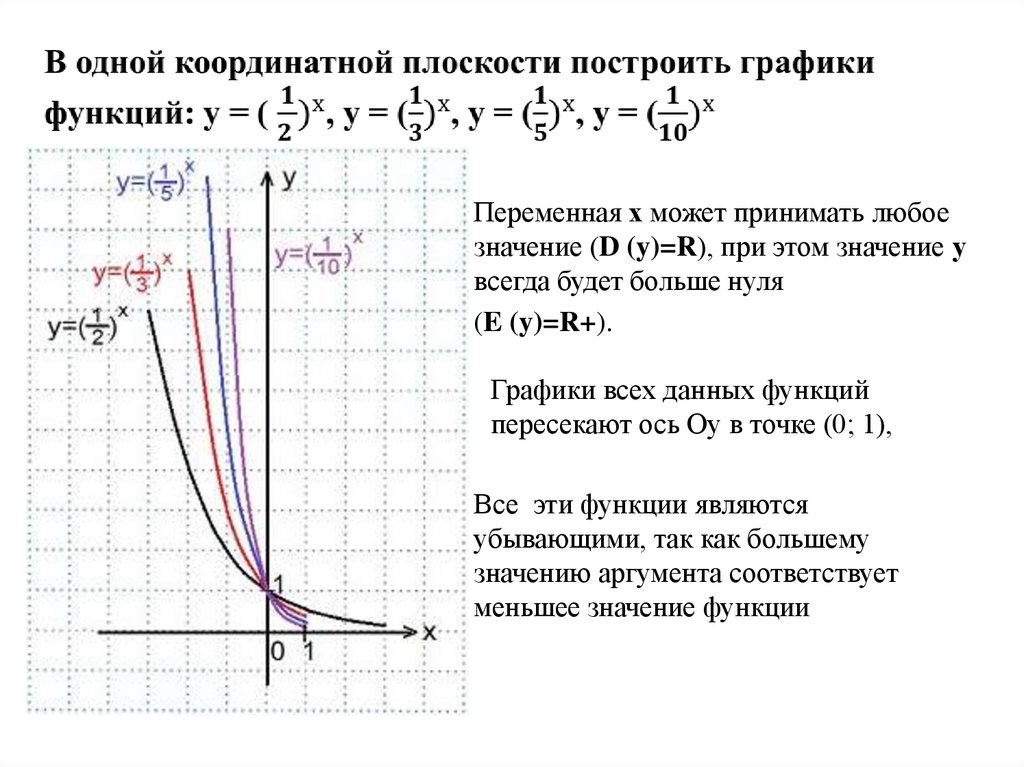
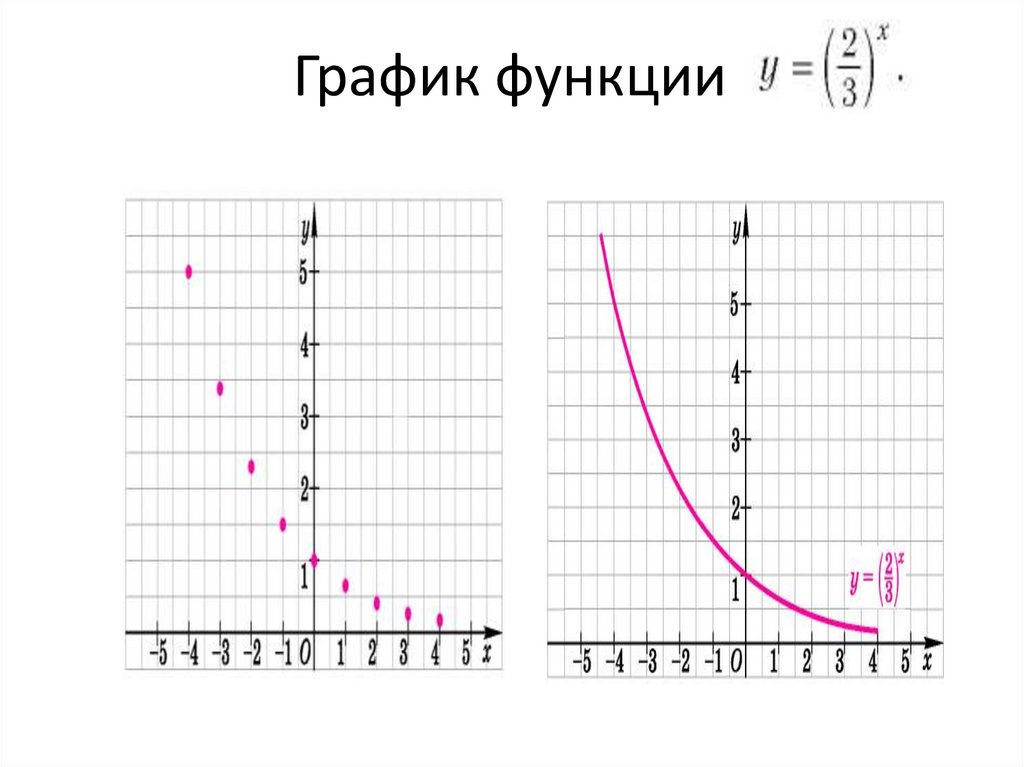
Переменная х может принимать любоезначение (D (y)=R), при этом значение у
всегда будет больше нуля
(E (y)=R+).
Графики всех данных функций
пересекают ось Оу в точке (0; 1),
Все эти функции являются
убывающими, так как большему
значению аргумента соответствует
меньшее значение функции
14.
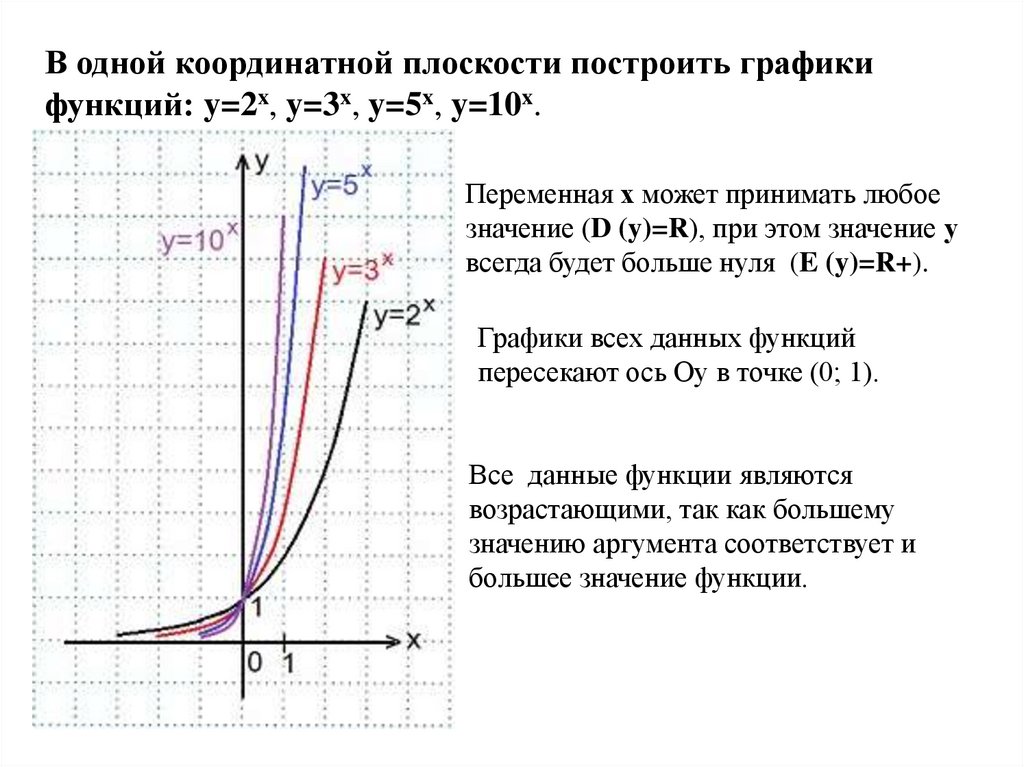
В одной координатной плоскости построить графикифункций: y=2x, y=3x, y=5x, y=10x.
Переменная х может принимать любое
значение (D (y)=R), при этом значение у
всегда будет больше нуля (E (y)=R+).
Графики всех данных функций
пересекают ось Оу в точке (0; 1).
Все данные функции являются
возрастающими, так как большему
значению аргумента соответствует и
большее значение функции.
15. График функции
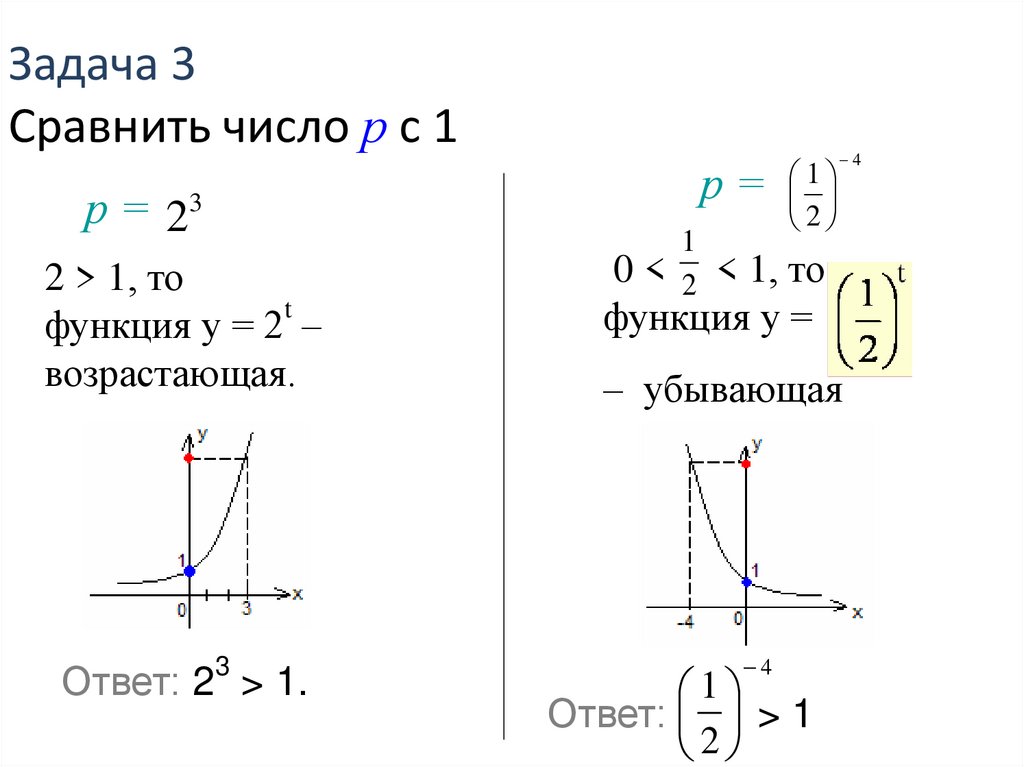
16. Задача 3 Cравнить число р с 1
р= 2р=
3
2 > 1, то
t
функция у = 2 –
возрастающая.
3
Ответ: 2 > 1.
1
2
4
1
0 < 2 < 1, то
функция у =
– убывающая
4
1
Ответ: > 1
2
17. Определение
Уравнение, в котором переменнаясодержится в показателе степени,
называется показательным.
Примеры:
3 81;
х
9 5 3 6 0
х
х
18. Простейшее показательное уравнение – это уравнение вида
a a , где a 0, a 1.x
b
Простейшее показательное
уравнение решается с
использованием свойств степени.
a a x b
x
b
19.
Способы решенияпоказательных уравнений.
1. Уравнивание оснований.
2. Вынесение общего множителя за скобки.
3. Метод почленного деления
4. Введение вспомогательной переменной
(замена переменной).
5. Графический способ решения.
20.
1. УРАВНИВАНИЕ ОСНОВАНИЙa
f ( x)
a
g ( x)
f ( x) g ( x)
21.
Показательное уравнение сводится к видуa a , a 0, a 1
x
b
Такое уравнение имеет единственный корень
x b
22.
УРАВНИВАНИЕ ОСНОВАНИЙ4
x 1
4
2
x 1 2
x 3
23.
УРАВНИВАНИЕ ОСНОВАНИЙх 2
3 81
х 2
4
3 3
х 2 4
х 2
Ответ : х 2
1
2
16
х
4
2 2
х 4
х
Ответ : х 4
24. УРАВНИВАНИЕ ОСНОВАНИЙ
3 27 0x
25. УРАВНИВАНИЕ ОСНОВАНИЙ
3 x 27 03 x 27
3 x 33
x 3
Ответ: x 3
26.
Решите уравнение:2
3 х
16
27.
Решите уравнение:2
3 х
16
Ответ: х=-1
28.
Решить уравнение3
х 2
1
Ответ: решений нет
29. Алгоритм:
1. Уединить слагаемое, содержащеепеременную
2. Привести степени к одному основания
3. Приравнять показатели
4. Решить полученное уравнение
5. Записать ответ
30.
Решите уравнение (1 способ)5
4 х 13
25
Решение
54 х 13 52
4 х 13 2
4 х 2 13
4 х 11
х 2,75
Ответ: - 2,75
31.
2. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИнеобходимо в левой части уравнения
вынести за скобки общий множитель с
меньшим показателем
a
a
x 1
x 1
a
x 1
b
a 1 b
2
a m n a m a n
32. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
3х 2
3 30
х
3 3 3 30
х
2
3 (3 1) 30
х
2
х
3 10 30
х
3 3
х
х 1
Ответ : х 1
a
m n
a
m
a
n
33. Как свести уравнение к простейшему показательному?
Как свести уравнение 3x 3x 2 72к простейшему показательному?
3 3 3 72
x
x
2
3 (1 9) 72
x
3 9
x 2
x
34. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
3 3x
x 3
78
3 1 3 78
x
3
3 26 78
x
3 3
x 1
x
Ответ:
x 1
35. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
3x 1
2 3
x 2
25
36. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
3x 1
3
x 2
3
2 3
x 2
25
3 2 25
3
x 2
25 25
x 2
3 1
x 2 0
x 2
37.
ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ2
х 4
6 2 80
х
Решение
2 2 6 2 80
х
4
х
2 (16 6) 80
х
2 х 10 80
2 8
х
2 х 23
х 3
Ответ: 3
38.
ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ81 9 х 9 0
3х
3х
Решение
9 (81 х) 0
3х
9 0
или
81 х 0
Нет решения
х - 81
3х
Ответ: -81
39. Однородные уравнения
Показательные уравнения виданазываются однородными
a
f ( x)
b
f ( x)
40.
3. Метод почленного деления на степеньМожно разделить обе части уравнения на
выражение, не равное нулю b x
a b
x
x
x
a
1
x
b
x
a
1
b
41.
Данный метод заключается в том, чтобы разделить каждый членуравнения содержащий степени с одинаковыми показателями, но с
разными основаниями, на одну из степеней.
Этот метод применяется для решения однородных показательных
уравнений.
42. Метод почленного деления на степень
2 3x
x
x
x
2
3
x
x
3
3
x
2
1
3
x
2
2
3
3
x 0
Ответ:
x 0
0
43. Метод почленного деления на степень
3 7x
3
1
x
7
x
x
x
3
1
7
x 0
44.
4. ВВЕДЕНИЕ новой ПЕРЕМЕННОЙНекоторые показательные
x
уравнения заменой a t сводятся
к квадратным.
Надо помнить, что t>0, так как
показательная функция не может
принимать значения отрицательные и
равные нулю
45. Введение новой переменной
42x
5 4 4 0
x
Пусть
4x t
t>0
t 2 5t 4 0
D 25 16 9
Тогда уравнение примет вид:
t1
5 3
4
2
4 4
x
x 1
Ответ:
t2
5 3
1
2
x
0
4
4
4 1;
x
x 0
x 1; x 0.
46. ВВЕДЕНИЕ новой ПЕРЕМЕННОЙ
9 6 3 27 0х
х
3 t
х
t>0
3 6 3 27 0
2
t 6t 27 0 - квадратное уравнение
2х
х
D 144; t1 9; t2 3;
3 9
3 3
х
3 3
х 2
х
х
2
нет решений
Ответ : х 2
47. Введение новой переменной
9 4 3 45 0x
x
3 t, t 0
x
t 4t 45 0
t1 9, t2 5
2
3 9
x
x 2
48. Уравнение
4 x 2 x 1 24 0Является ли показательным?
Как его можно преобразовать?
Какой метод можно применить?
Метод введения новой переменной
2
2x
2 2 24 0
x
2 t, t 0
x
t 2 t 24 0
2
49. Алгоритм решения показательного уравнения методом введения новой переменной:
1. Определить возможность переписать данное уравнение в новомвиде, позволяющем ввести новую переменную
2.Вводим новую переменную
3.Решаем уравнение относительно новой переменной
4. Записываем ответ
50. 5. ГРАФИЧЕСКИЙ МЕТОД
1. Построить графики двух функций (левая иправая части уравнения)
2. Найти точки пересечения графиков, если они
есть
3. Найти абсциссы точек пересечения графиков
4. Записать ответ
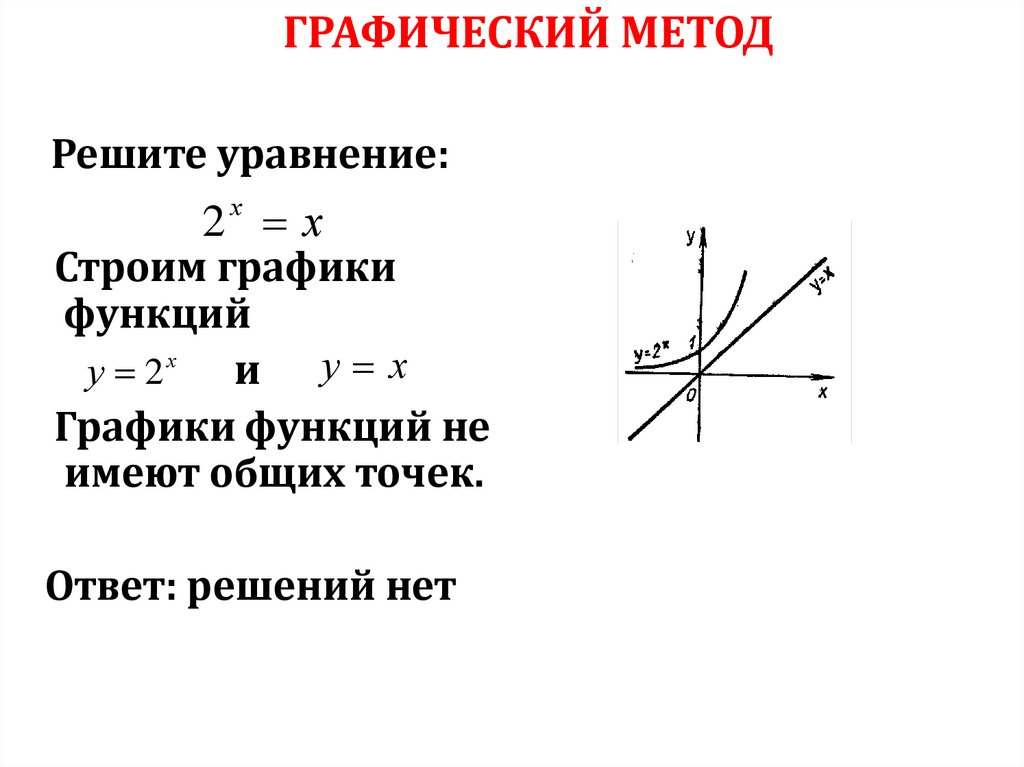
51.
ГРАФИЧЕСКИЙ МЕТОДРешите уравнение:
2х х
Строим графики
функций
у 2х
и у . х
Графики функций не
имеют общих точек.
Ответ: решений нет
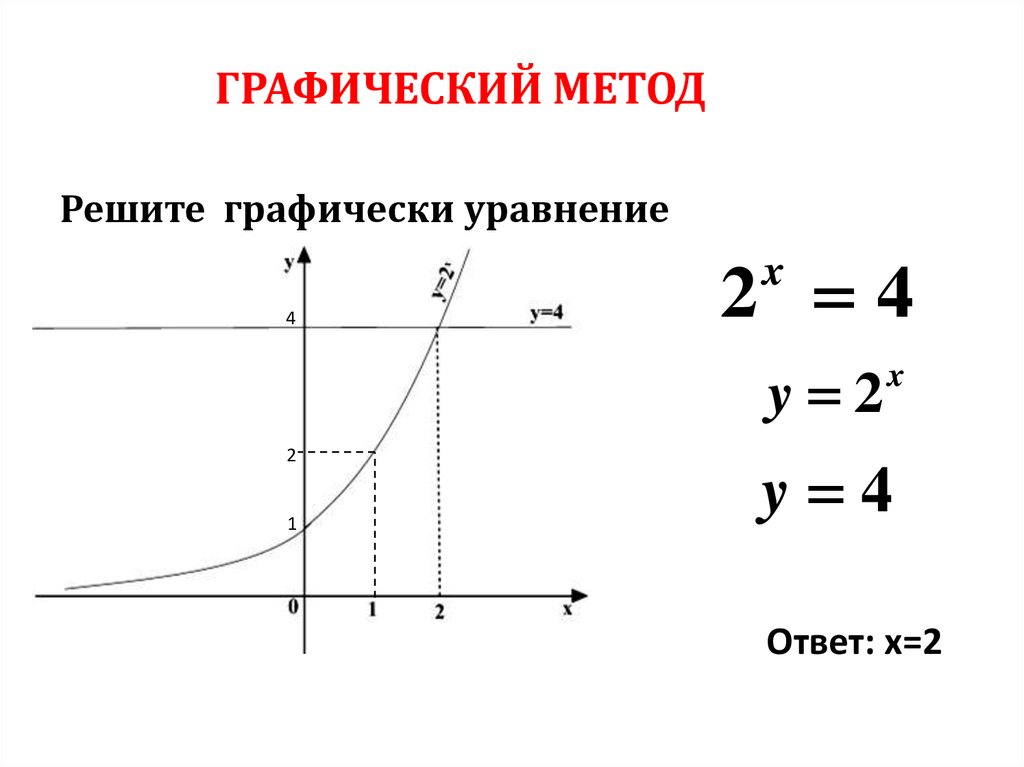
52. ГРАФИЧЕСКИЙ МЕТОД
Решите графически уравнение2 4
x
4
y 2
2
1
x
y 4
Ответ: х=2
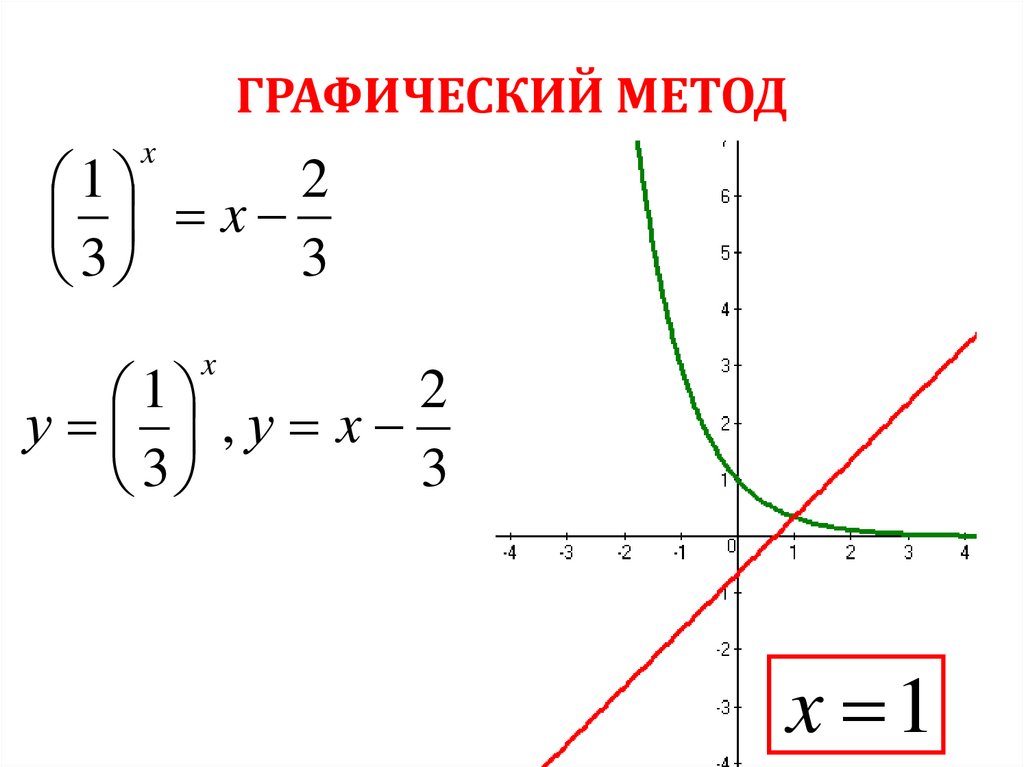
53.
ГРАФИЧЕСКИЙ МЕТОДx
2
1
x
3
3
x
2
1
у ,у x
3
3
x 1
54.
ГРАФИЧЕСКИЙ МЕТОД1)4 5 х,
х
Решением уравнения является
абсцисса точки пересечения
графиков функций
у 4 х и у 5 х см. рисунок .
Проверка :
41 5 1
4 4 верно
Ответ : 1.
55. Способы решения показательных уравнений
Аналитические:1. Приравнивание
показателей
2. Вынесение общего
множителя за
скобки
3. Использование
однородности
4. Введение новой
переменной
5. Графический
56. Определите способ решения уравнений:
1)3 2 0x
x
(однородное уравнение)
x
1 1
2 ) 0
3 3
(приравнивание показателей)
3)25x 5x 2 0
4) 2
x
1
2
(замена переменной)
(приравнивание показателей)
5)52 x 1 52 x 3 4,8
(вынесение за скобки)
57.
58.
ЧТО ЗНАЧИТрешить неравенство?
Решить неравенство
значит, найти все его
решения или доказать,
что решений нет.
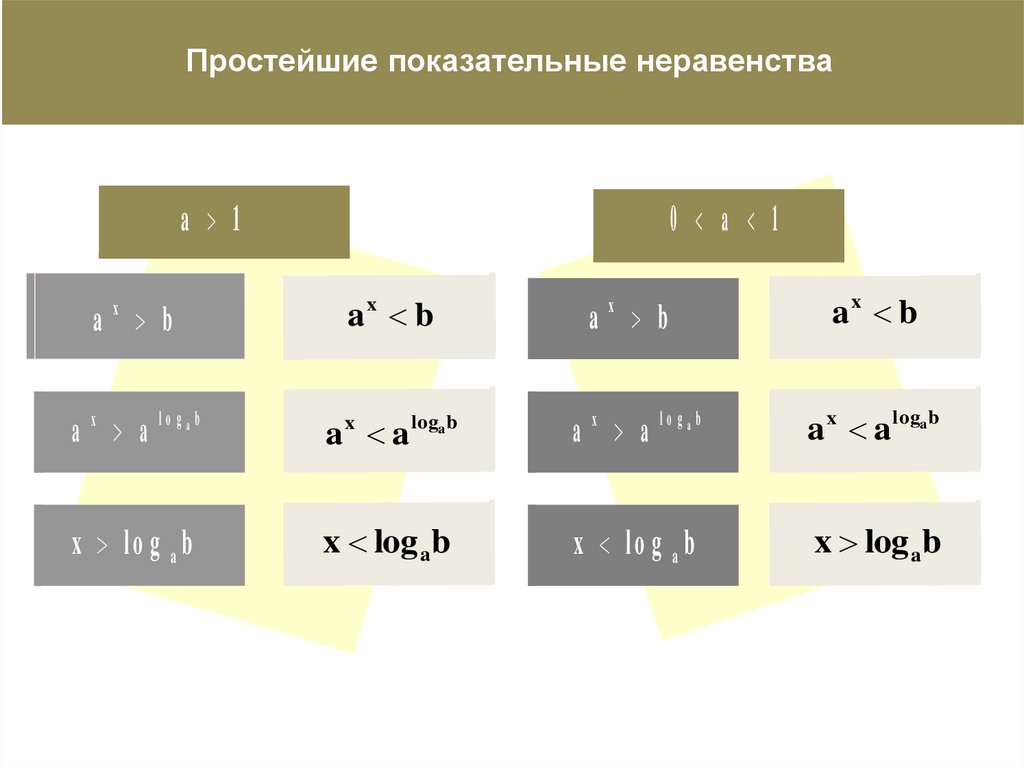
59.
Простейшие показательные неравенстваa 1
0 a 1
a b
ax b
ax b
ax b
a x a lo g ab
a a
loga b
a x a lo g ab
a x a logab
x lo g a b
x log ab
x lo g a b
x log ab
x
x
60.
2 16Пример №1.
x
РЕШЕНИЕ:
2x 16,
2 x 2 4 , у 2t 2 1 возрастает на всей
области определения,
х 4.
Ответ: х ; 4
61.
x1
125
5
Пример №2.
РЕШЕНИЕ:
x
1
125,
5
x
3
1 1
,
5 5
х 3.
Ответ: х
; 3
t
1
1
y 0 1
5
5
убывает на всей
области
определения,
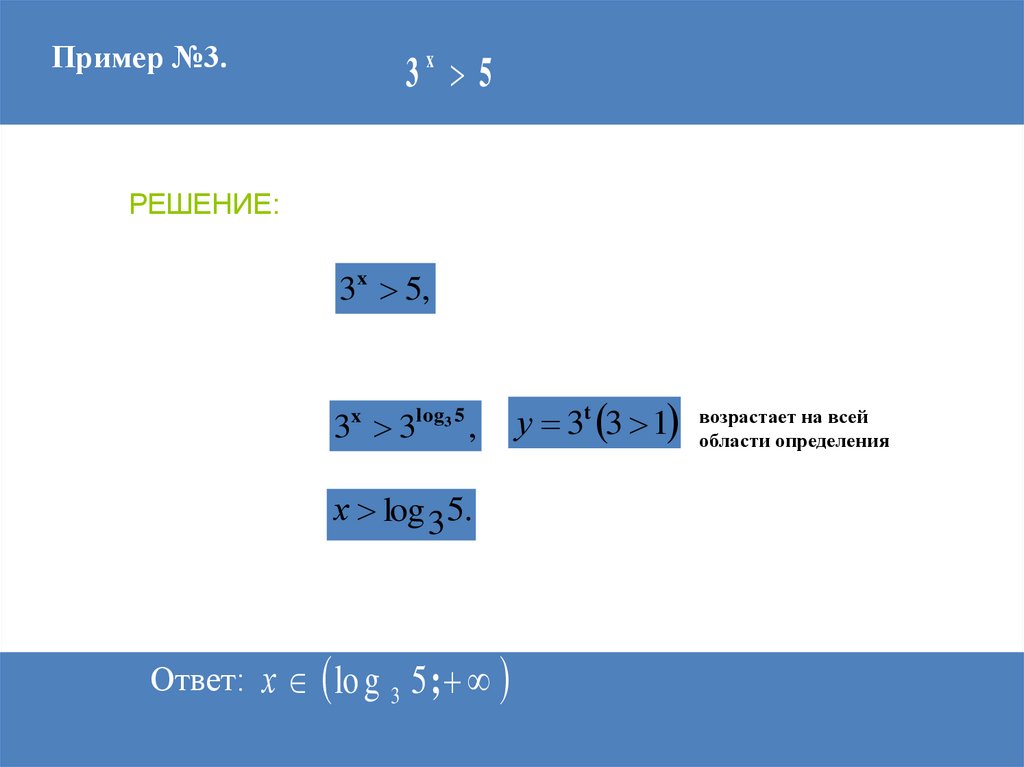
62.
Пример №3.3x 5
РЕШЕНИЕ:
:
3x 5,
3x 3log3 5 ,
х log 3 5.
Ответ: х lo g 3 5 ;
на всей
у 3t 3 1 возрастает
области определения
63.
Показательные неравенства, приводимые к простейшимПример №4.
РЕШЕНИЕ:
3
3
х 1
х 2
х 1
х 2
9
32 , y 3t 3 1
x 1
2,
x 2
x 1
2 0,
x 2
x 5
0,
x 2
Ответ: х 2 ; 5
2 x 5.
возрастает на всей
области определения
64.
4 3Пример №6.
РЕШЕНИЕ:
1 3
x 2 2x 1
3 x 2x 1 1,
x 2 2x 1
3
9;
2
x2 2x 1
4 3
5 4
x 2 2x 1
5 4,
9,
3x 2x 1 30 ,
x 2 2x 1
3
32 ;
2
y 3t 3 1 возрастает на всей
области определения
1 x 3,
x 1 2 ,
2
x 1 2 ,
x 2x 1 0,
2
x 1 2 ; 1 x 3,
x 2x 1 2;
1 x 3, x 1 2 ;
Ответ: х 1 ;1
2 1 2 ;3
1 x 1 2 ,
1 2 x 3.
65.
Показательные неравенства,приводимые к квадратным неравенствам
22x 2 3 2x ,
Пример №7. 2 2 x 2 3 2 x
2 2x 3 2 x 2 0.
Пусть 2
x
t, t 0, тогда
t 2 3t 2 0,
t 0;
t 1,
t 2,
t 0;
Вернёмся к переменной х
t 0,
t 1,
t 0,
t 2;
0 2 x 1,
x
2 x 0 при x R
2 2;
t
функция y 2 2 1
возрастает при всех х
из области определения
0 t 1,
t 2.
2 x 1,
x
2 2;
2 x 20 ,
x
2 2;
x 0,
x 1. Ответ: х ; 0 1;
66.
Однородные показательные неравенства первой степениx
1 1
2 2
Пример №8.
x
РЕШЕНИЕ:
1
1
2
2
1
2
x 2
1
2
1
2
5
x 2
5,
1 2
1 5,
2
x 2
5
5,
4
x 2
4,
2 2 x 2 2 ,
2 x 2,
x 0.
Ответ:
x 2
х ;0
y 2t 2 1
возрастает на всей
области определения
67.
Однородные показательные неравенства второй степени3 4 x 2 9 x 5 6 x 0,
Пример №9.
3 2 5 2 3 2 3 0,
x
2x
2x
3 4 x 2 9 x 5 6 x 0
3 2 2x 5 2 x 3 x 2 3 2x 0, 3 2x 0, при x R
22x
2x 3x
32x
3 2x 5 2x 2 2x 0,
3
3
3
2x
x
2
2
3 5 2 0.
3
3
Вернёмся к переменной х
x
x
x
2
Замена : t , t 0, тогда
3
2
3t 2 5t 2 0,
t 1, 2 t 1.
3
3
t 0;
t 0;
0
r
2 2
2 2 2
2
2
1,
, y 0 1 убывает на всей области
3 3
3 3 3
3
3
определения
0 x 1.
Ответ: х 0 ;1
68.
Показательные неравенства,приводимые к рациональным неравенствам
Пример №10.
x 1
2 2
3 0,
x
x 1
2
2
3 0
2
x
2 x 3 0,
2
x
Пусть 2 t, t 0, тогда
2
2
t
3t
2
2
t
3
0,
t
3t 2 0, 1 t 2,
0,
t
t
t 0;
t
0;
t 0;
t 0;
x
1 t 2.
Вернёмся к переменной х
1 2x 2,
y 2r 2 1
возрастает на всей
области определения
0 x 1.
Ответ: х 0;1
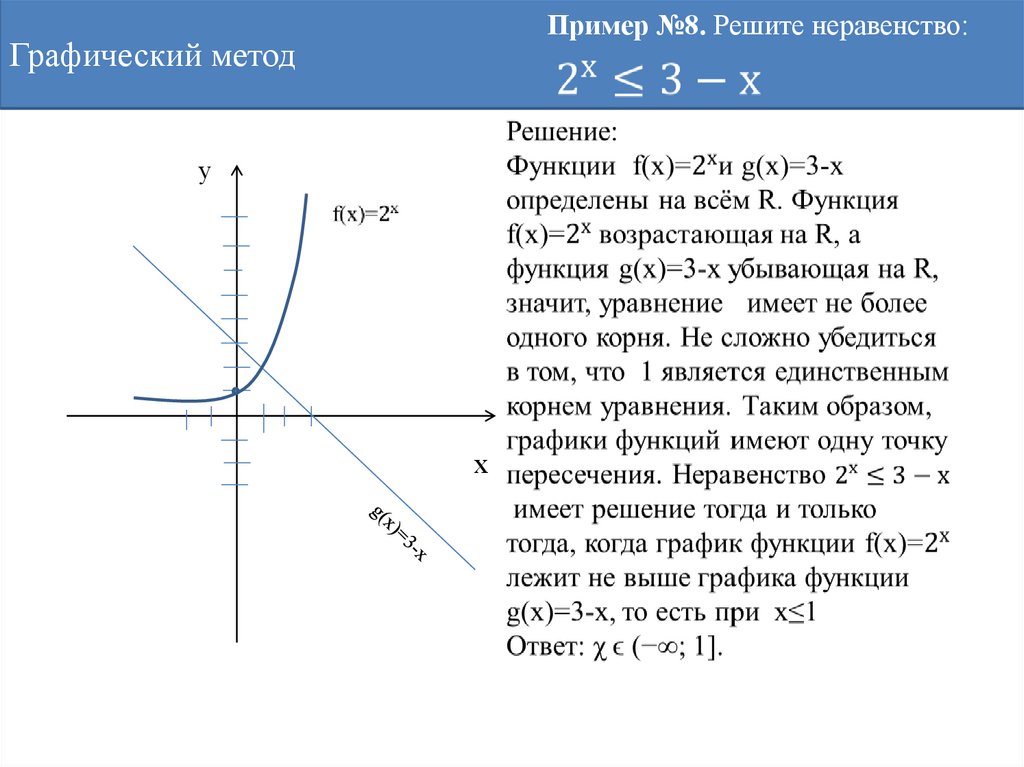
69.
Пример №8. Решите неравенство:Графический метод
у
х












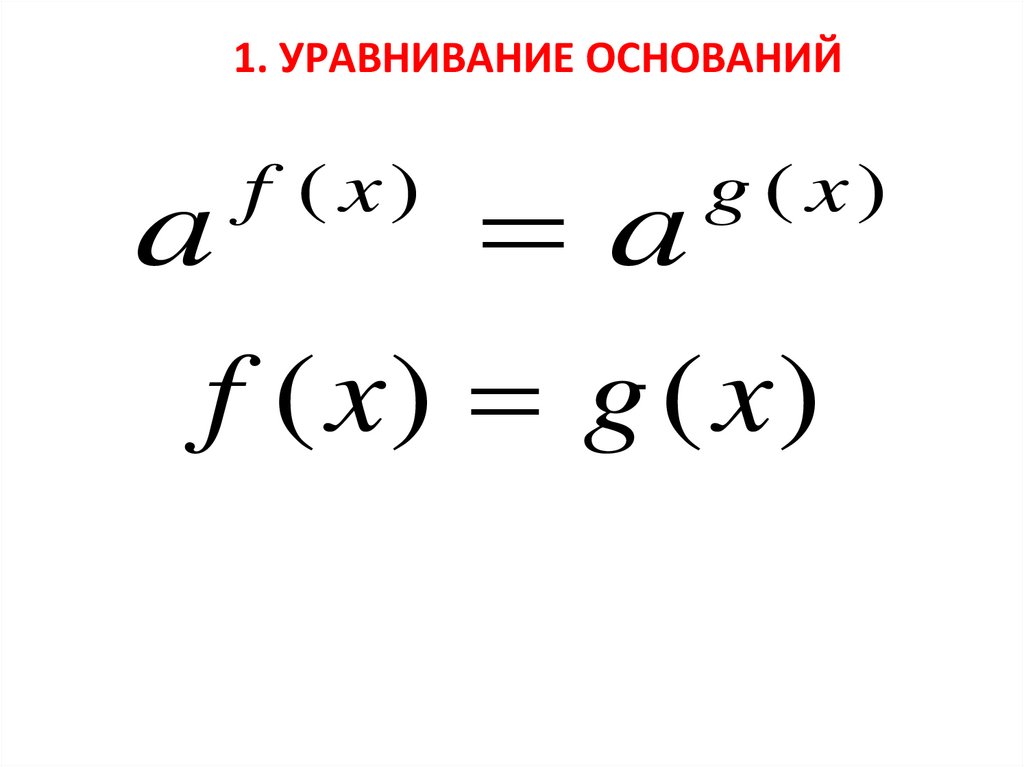
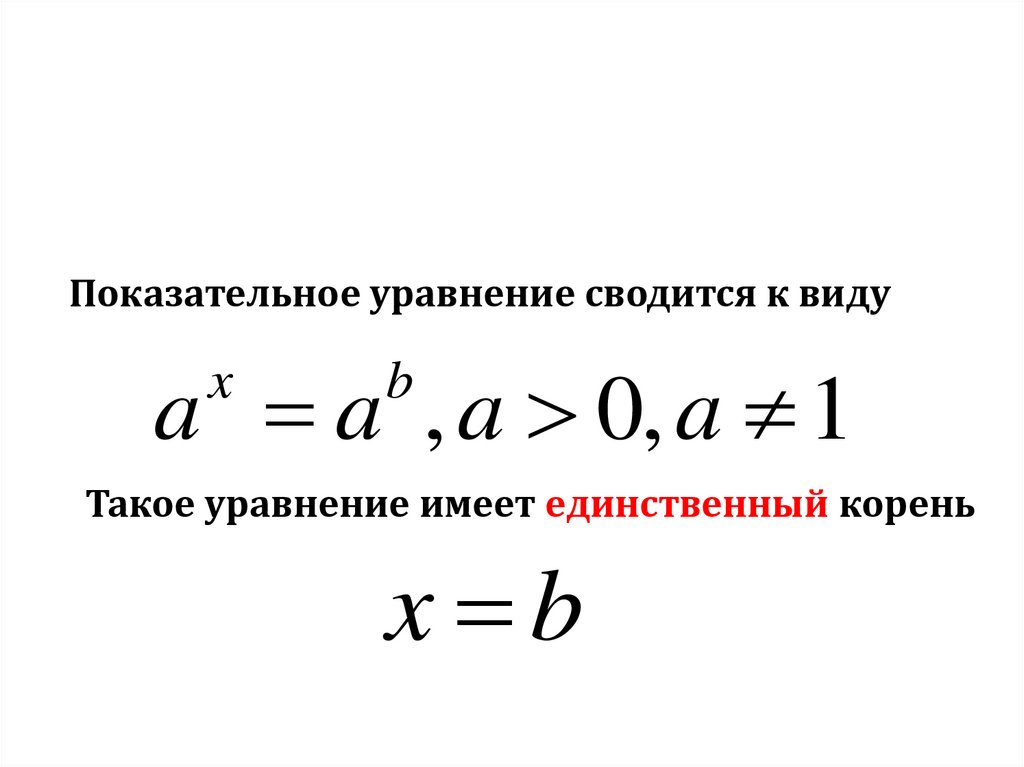









































 mathematics
mathematics








