граф пред множеств

1.

Графическое
представление
множеств

2.

В одной из своих работ выдающийся математик,
физик и механик Леонард Эйлер предложил для
решения задач использовать геометрические
схемы в виде кругов (диаграммы Эйлера).
Эти схемы помогают наглядно показать отношения
между множествами: пересечение, объединение,
включение одного множества в другое.
Родился 15 апреля 1707 года в
Базеле (Швейцария);
умер в 1783 году в Санкт-Петербурге.

3.

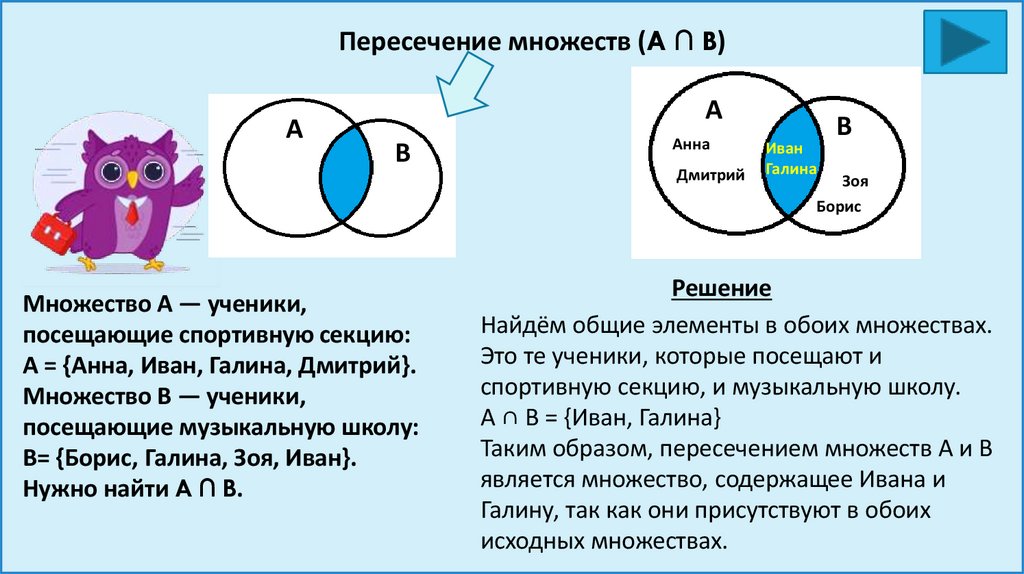
Пересечение множеств (A ∩ B)
A
A
B
Множество A — ученики,
посещающие спортивную секцию:
A = {Анна, Иван, Галина, Дмитрий}.
Множество B — ученики,
посещающие музыкальную школу:
B= {Борис, Галина, Зоя, Иван}.
Нужно найти A ∩ B.
Анна
Дмитрий
Иван
Галина
B
Зоя
Борис
Решение
Найдём общие элементы в обоих множествах.
Это те ученики, которые посещают и
спортивную секцию, и музыкальную школу.
A ∩ B = {Иван, Галина}
Таким образом, пересечением множеств A и B
является множество, содержащее Ивана и
Галину, так как они присутствуют в обоих
исходных множествах.

4.

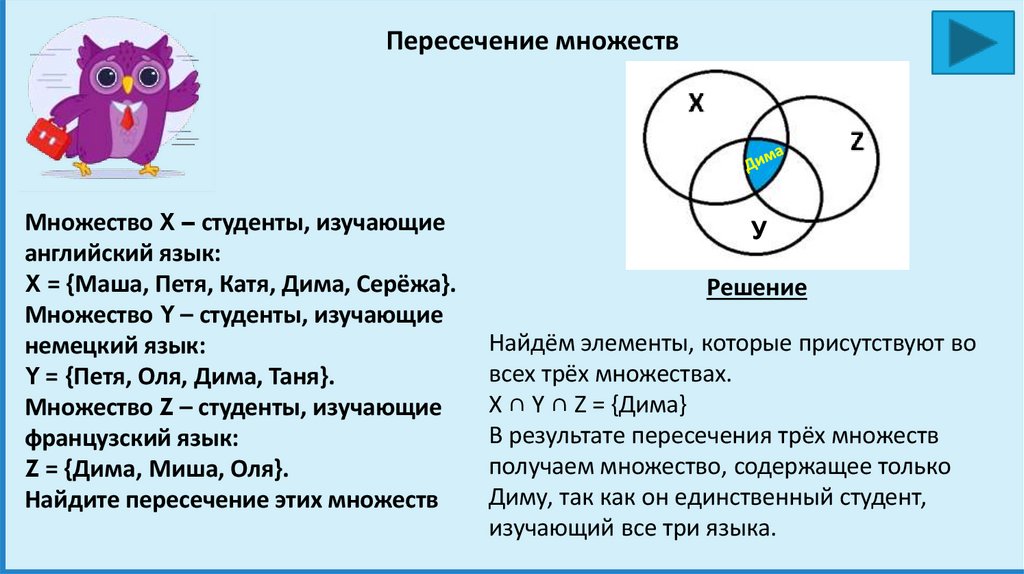
Пересечение множеств
Множество X – студенты, изучающие
английский язык:
X = {Маша, Петя, Катя, Дима, Серёжа}.
Множество Y – студенты, изучающие
немецкий язык:
Y = {Петя, Оля, Дима, Таня}.
Множество Z – студенты, изучающие
французский язык:
Z = {Дима, Миша, Оля}.
Найдите пересечение этих множеств
У
Решение
Найдём элементы, которые присутствуют во
всех трёх множествах.
X ∩ Y ∩ Z = {Дима}
В результате пересечения трёх множеств
получаем множество, содержащее только
Диму, так как он единственный студент,
изучающий все три языка.

5.

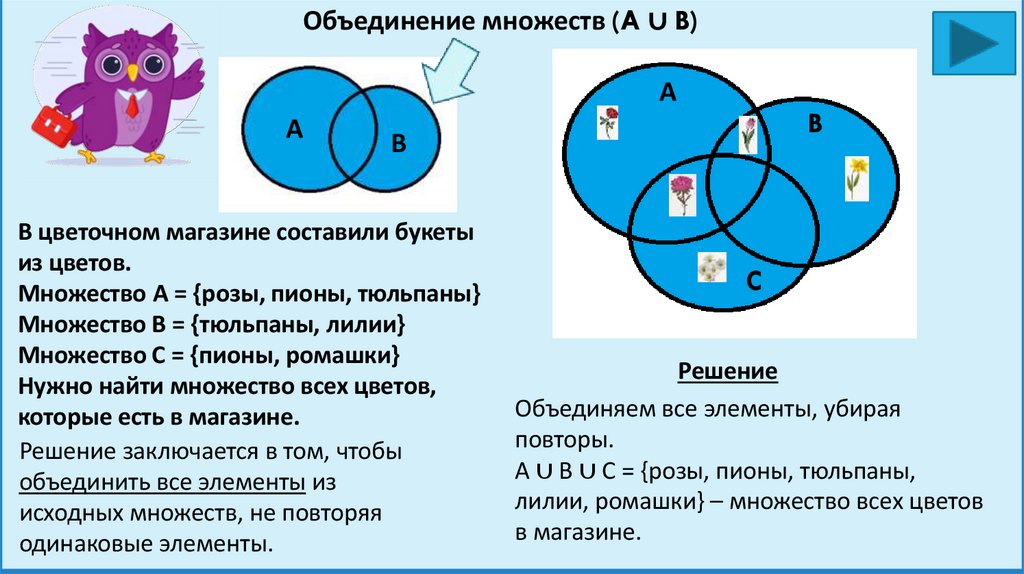
Объединение множеств (A ∪ B)
А
A
B
B
В цветочном магазине составили букеты
из цветов.
Множество A = {розы, пионы, тюльпаны}
Множество B = {тюльпаны, лилии}
Множество C = {пионы, ромашки}
Нужно найти множество всех цветов,
которые есть в магазине.
Решение заключается в том, чтобы
объединить все элементы из
исходных множеств, не повторяя
одинаковые элементы.
C
Решение
Объединяем все элементы, убирая
повторы.
A ∪ B ∪ C = {розы, пионы, тюльпаны,
лилии, ромашки} – множество всех цветов
в магазине.

6.

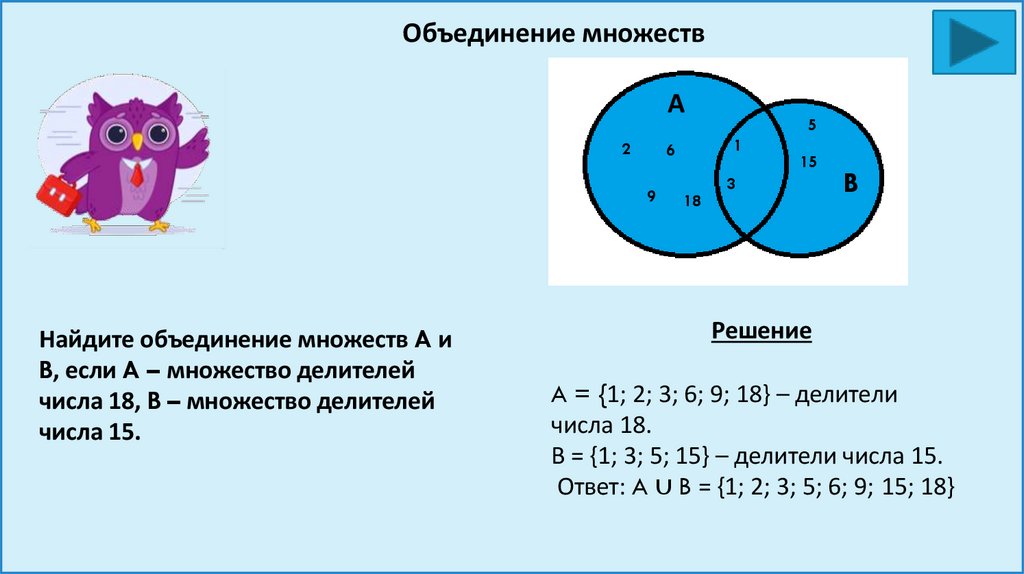
Объединение множеств
А
2
6
9
Найдите объединение множеств A и
B, если A – множество делителей
числа 18, B – множество делителей
числа 15.
5
1
18
15
3
B
Решение
A = {1; 2; 3; 6; 9; 18} – делители
числа 18.
В = {1; 3; 5; 15} – делители числа 15.
Ответ: A ∪ B = {1; 2; 3; 5; 6; 9; 15; 18}

7.

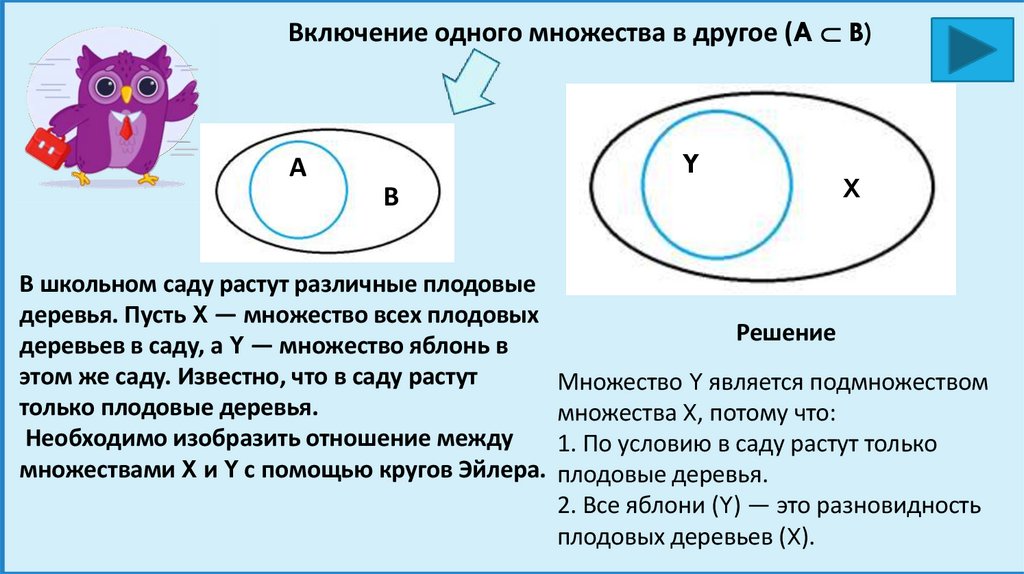
Включение одного множества в другое (A B)
Y
A
B
X
В школьном саду растут различные плодовые
деревья. Пусть X — множество всех плодовых
Решение
деревьев в саду, а Y — множество яблонь в
этом же саду. Известно, что в саду растут
Множество Y является подмножеством
только плодовые деревья.
множества X, потому что:
Необходимо изобразить отношение между
1. По условию в саду растут только
множествами X и Y с помощью кругов Эйлера. плодовые деревья.
2. Все яблони (Y) — это разновидность
плодовых деревьев (X).

8.

При графическом представлении множеств нужно помнить:
1. Каждый круг изображает какое-то множество.
2. Размер кругов не важен, можно использовать и другие
геометрические фигуры. Важно их взаимное
расположение.
3. Непересекающиеся множества (т.е. у них нет общих
элементов, A ∩ B = ∅) изображаются непересекающимися
кругами.
A
B

9.

Всё ли вам понятно по сегодняшней теме?
Есть ли какие-то моменты, которые требуют
дополнительного разъяснения?