Магнитные свойства вещества

1. Магнитные свойства вещества. Молекулярные токи. Диа-, пара- и ферромагнетики. Вектор намагниченности. Магнитная восприимчивость

и магнитная
проницаемость.

2.

• Мы рассматривали проводники с током, находящиеся в вакууме
• Что будет с м.п., если поместить проводник в вещество?
• Опыт: магнитное поле в веществе зависит от свойств вещества,
описываемых магнитной проницаемостью
• Вещество, способное намагничиваться под действием магнитного
поля (приобретать магнитный момент), называется магнетиком
• Все природные вещества в той или иной мере обладают
магнитными свойствами
• Результирующее после внесения магнетика поля В:
• где В0- внешнее поле, В’- магнитное поле намагниченного
вещества
• Физическая величина, показывающая, во сколько раз индукция
магнитного поля в однородной среде отличается по модулю от
индукции магнитного поля в вакууме, называется магнитной
проницаемостью: B
B0

3.

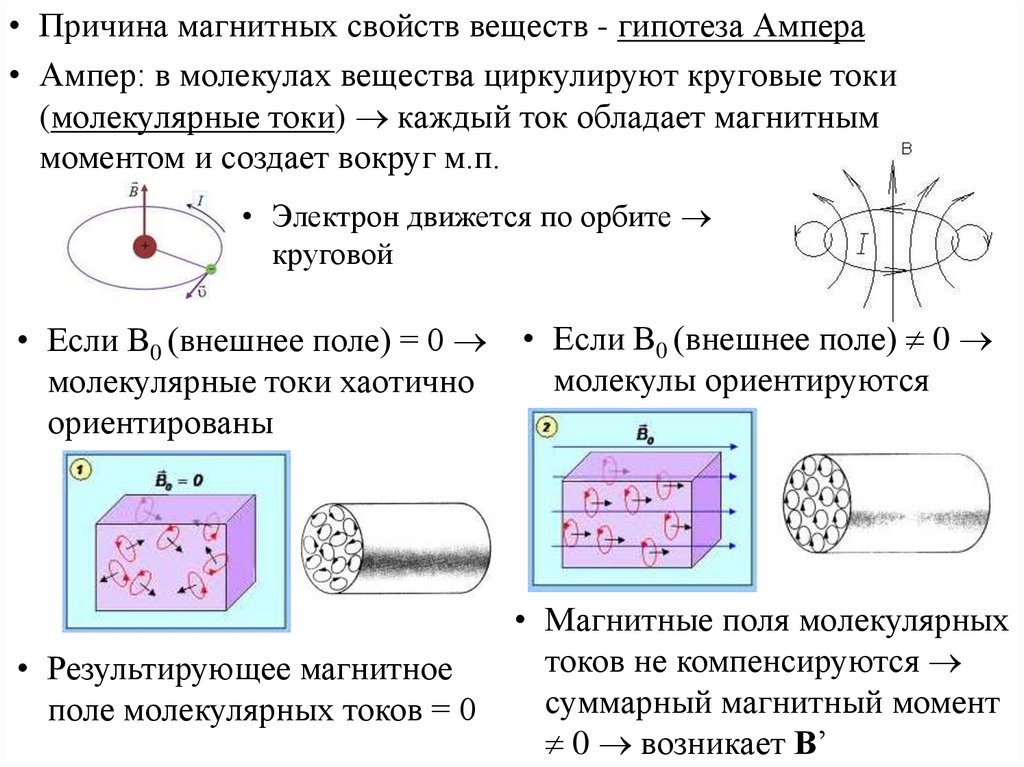
• Причина магнитных свойств веществ - гипотеза Ампера
• Ампер: в молекулах вещества циркулируют круговые токи
(молекулярные токи) каждый ток обладает магнитным
моментом и создает вокруг м.п.
• Электрон движется по орбите
круговой
• Если В0 (внешнее поле) = 0
молекулярные токи хаотично
ориентированы
• Результирующее магнитное
поле молекулярных токов = 0
• Если В0 (внешнее поле) 0
молекулы ориентируются
• Магнитные поля молекулярных
токов не компенсируются
суммарный магнитный момент
0 возникает В’

4.

• Степень намагничения магнетика характеризуется магнитным
моментом единицы объема, называемой вектором
намагничивания J:
• где pm – магнитный момент отдельной молекулы, V – физически
бесконечно малый объем в окрестности точки (суммируются все
магнитные моменты в данном малом объеме)
• Усреднённые по объему молекулярные токи называют токами
намагничивания I’.
• Обычные токи, текущие проводникам, связаны с перемещением в
веществе носителей тока, их называют токами проводимости I
• Сечение однородного проводника: молекулярные токи соседних
атомов направлены навстречу друг другу и взаимно
компенсируются остаются некомпенсированные
токи на боковой поверхности они образуют
поверхностный ток намагничивания – он возбуждает
макроскопическое м.п.

5.

• Сечение неоднородного проводника:
толщина линий соответствует
силе молекулярных токов
вектор j растет с ростом координат X
компенсации молекулярных токов нет
макроскопический объемный ток
намагничивания , текущий в направлении Y
• Пусть есть магнетик и результирующее м.п.:
• Тогда поток через произвольную замкнутую поверхность:
• Линии магнитной индукции всегда замкнуты (поле вихревое)
число линий входящих внутрь поверхности = числу линий
выходящих наружу правая часть = 0
• Теорема Гаусса для вектора B:поток вектора магнитной индукции
через любую замкнутую поверхность равен нулю:

6.

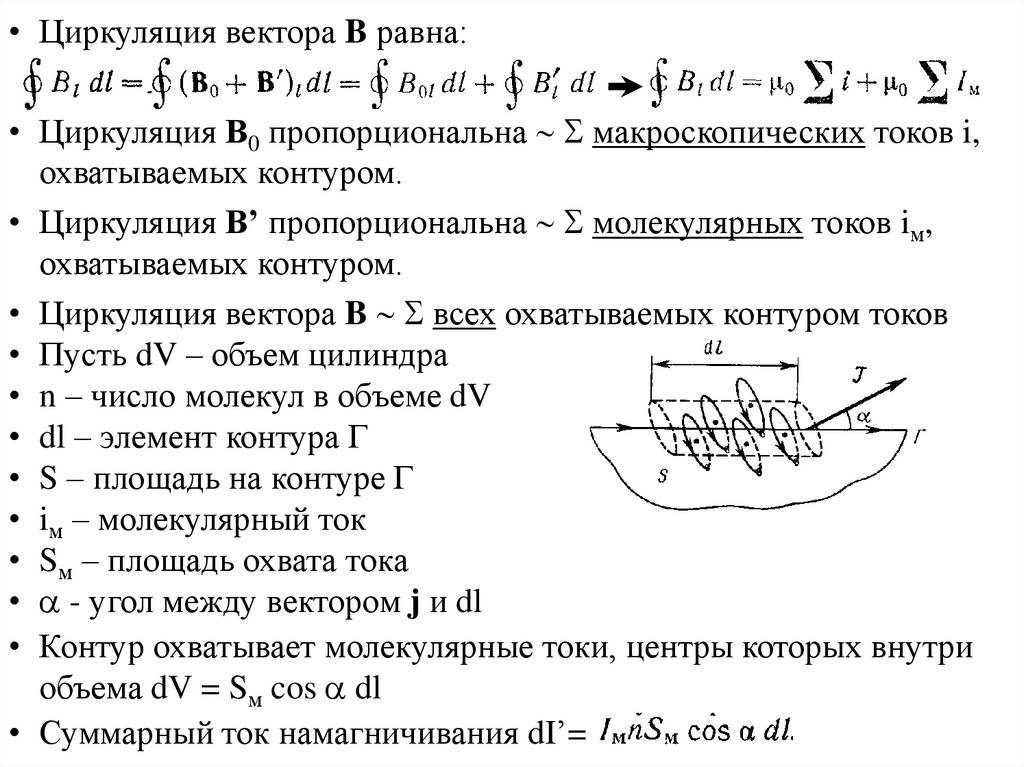
• Циркуляция вектора B равна:
• Циркуляция В0 пропорциональна макроскопических токов i,
охватываемых контуром.
• Циркуляция В’ пропорциональна молекулярных токов iм,
охватываемых контуром.
• Циркуляция вектора B всех охватываемых контуром токов
• Пусть dV – объем цилиндра
• n – число молекул в объеме dV
• dl – элемент контура Г
• S – площадь на контуре Г
• iм – молекулярный ток
• Sм – площадь охвата тока
• - угол между вектором j и dl
• Контур охватывает молекулярные токи, центры которых внутри
объема dV = Sм cos dl
• Суммарный ток намагничивания dI’=

7.

• Магнитный момент отдельного молекулярного тока: pm=IмSм
• Тогда магнитный момент единицы объема вещества есть модуль
вектора J: |J| = IмSмn,
• Тогда проекция вектора J на направление dl: Jl = IмSмn cos
• Т.е. сумма молекулярных токов, охватываемых элементом dl:
• Тогда, подставив в циркуляцию вектора B, получим:
• Напряженность магнитного поля H (аналог электрической
индукции) определяется соотношением:
• Теорема о циркуляции вектора Н:циркуляция вектора Н по
произвольному замкнутому контуру равна алгебраической сумме
токов проводимости, охватываемых этим контуром:
макроскопические токи
распределены в пространстве с
плотностью j

8.

• Связь между векторами J, В, H:
• где - магнитная восприимчивость –безразмерная величина.
• где =1+4 - магнитная проницаемость вещества показывает, во
сколько раз усиливается поле в магнетике
• Результирующее м.п.: В = В0
= В/В0
• Все магнетики по свойствам делятся на:
• диамагнетики: <1 >0 (алюминий, платина, кислород) J H
• парамагнетики: >1 <0 (медь, серебро, висмут) J H
• ферромагнетики: >>1 (железо, кобальт, никель) J(H) –
сложный характер

9.

Все магнетики принято делить на три класса:
1) парамагнетики – вещества, которые слабо намагничиваются в
магнитном поле, результирующее поле в парамагнетиках сильнее,
чем в вакууме > 1 (алюминий, платина, кислород и др.;)
2) диамагнетики – вещества, которые намагничиваются, но не
значительно, против поля, то есть поле в диамагнетиках слабее, чем
в вакууме, магнитная проницаемость < 1 (медь, серебро, висмут и
др.;)
3) ферромагнетики – вещества, способные сильно
намагничиваться в магнитном поле, > > 1 (железо, кобальт, никель
и некоторые сплавы)

10.

• Ферромагнетики: отличаются:
• высоким значением магнитной восприимчивости ;
• зависимостью магнитной проницаемости μ от напряженности
магнитного поля зависимость В от Н нелинейная;
• наличием петли гистерезиса на кривой намагничивания;
• существованием точки Кюри – температуры выше которой
ферромагнетик ведет себя как обычный парамагнетик.
• Намагничение ферромагнетиков зависит от Н сложным образом:
• Основная кривая намагничения
ферромагнетика (магнитный момент
первоначально был равен нулю)
• При достижении насыщения В продолжает расти по линейному
закону:
• Понятие магнитной проницаемости применимо только к
основной кривой намагничения

11.

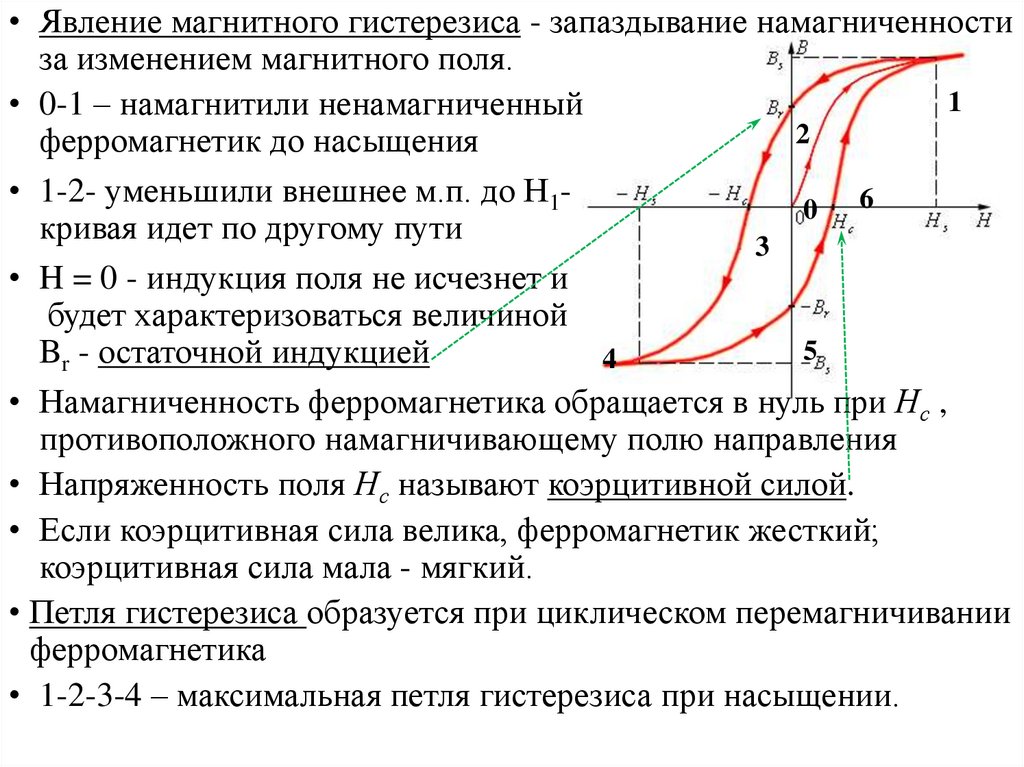
• Явление магнитного гистерезиса - запаздывание намагниченности
за изменением магнитного поля.
1
• 0-1 – намагнитили ненамагниченный
2
ферромагнетик до насыщения
• 1-2- уменьшили внешнее м.п. до Н10 6
кривая идет по другому пути
3
• H = 0 - индукция поля не исчезнет и
будет характеризоваться величиной
5
Br - остаточной индукцией
4
• Намагниченность ферромагнетика обращается в нуль при Нс ,
противоположного намагничивающему полю направления
• Напряженность поля Нс называют коэрцитивной силой.
• Если коэрцитивная сила велика, ферромагнетик жесткий;
коэрцитивная сила мала - мягкий.
• Петля гистерезиса образуется при циклическом перемагничивании
ферромагнетика
• 1-2-3-4 – максимальная петля гистерезиса при насыщении.

12.

• Электрон e вращается по орбите с частотой
• Заряд переносимый в единицу времени: Iм = e
• Т.к. e 0, то ток v I
• Магнитный момент электрона: pm=IмS=e r2,
• где r – радиус орбиты
• Скорость электрона: v=2 r
орбитальный
магнитный момент электрона
• Движущийся электрон обладает моментом импульса:
- орбитальный механический момент электрона
• Отношение магнитного момента элементарной частицы к её
механическому моменту называется гиромагнитным отношением
для электрона оно равно:
• где знак «-» т.к. L pm
• Магнитный момент атома = орбитальные и собственные
магнитны моменты электронов + магнитный момент ядра атома.

13.

Преломление линий магнитной индукции
• Рассмотрим границу двух однородных изотропных магнетиков с
различными :
• Цилиндр высоты h
• Основания S1 и S2 - по разные
стороны поверхности раздела.
• По теореме Гаусса:
• Потоком B через боковую поверхность цилиндра пренебрегаем,
т.к. h 0.
• Поток через верхнее основание цилиндра = B1nS1, где B1n нормальная составляющая вектора B в первом магнетике в
непосредственной близости к поверхности раздела.
• Поток через нижнее основание = B2nS2, где B2n – нормальная
составляющая вектора B во втором магнетике.
• Тогда Полный поток:

14.

• Равенство выполнится, если B1n = - B2n
• B1 и B2 спроектируем на одну нормаль B1n = B2n
• Заменим составляющие В соответствующими составляющими
вектора Н, умноженными на 0 , получим соотношение
• Теперь возьмем на границе магнетиков прямоугольный контур и
вычислим для него циркуляцию Н:
• Ширина контура а мала вкладом,
вносимым в циркуляцию сторонами,
перпендикулярными к поверхности
можно было пренебречь.
• Тогда:
= b(H1 – H2 )
• Контур не охватывает токов I =0 H1 = H2
• Заменим Н на В с учетом 0 :

15.

При переходе через границу раздела двух магнетиков
нормальная составляющая вектора В и тангенциальная
составляющая вектора Н изменяются непрерывно.
Тангенциальная же составляющая вектора В и нормальная
составляющая вектора Н при переходе через границу раздела
претерпевают разрыв.
Таким образом, при переходе через границу раздела двух сред
вектор В ведет себя аналогично вектору D, а вектор Н
аналогично вектору Е.

16.

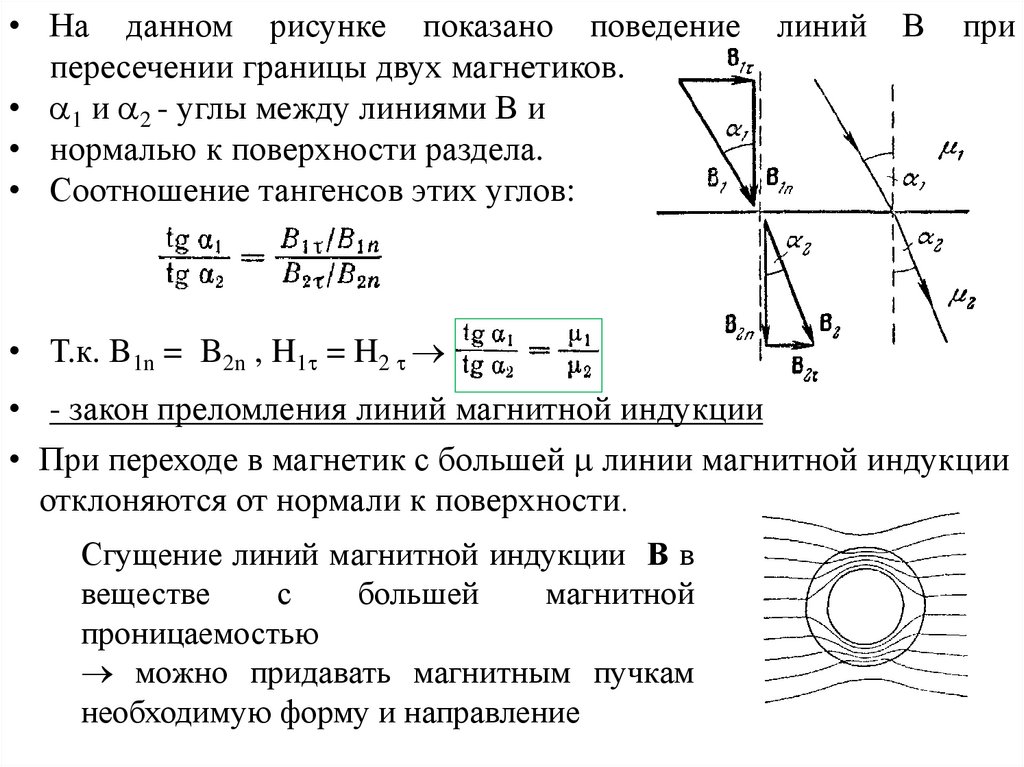
• На данном рисунке показано поведение
пересечении границы двух магнетиков.
• 1 и 2 - углы между линиями В и
• нормалью к поверхности раздела.
• Соотношение тангенсов этих углов:
линий
В
при
• Т.к. B1n = B2n , H1 = H2
• - закон преломления линий магнитной индукции
• При переходе в магнетик с большей линии магнитной индукции
отклоняются от нормали к поверхности.
Сгущение линий магнитной индукции В в
веществе
с
большей
магнитной
проницаемостью
можно придавать магнитным пучкам
необходимую форму и направление