https___school.mos.ru_ej_attachments_files_218_318_245_original_%D0%9B%D0%B5%D0%BA%D1%86%D0%B8%D1%8F%20%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C%20%D0%BF%D1%80%D1%8F% (3)

1.

Университетский лицей №1523
Предуниверситария НИЯУ МИФИ
Лекции по геометрии
10 класс
© Хомутова Лариса Юрьевна
© Крайко Мария Александровна

2.

Параллельность
прямой и плоскости

3.

Прямая a и плоскость называются параллельными,
если они не имеют общих точек: a a = .
Замечание: Через точку, лежащую вне данной плоскости, можно
провести бесконечно много прямых, параллельных данной
плоскости (к примеру, всякая прямая, лежащая в плоскости
потолка комнаты, параллельна плоскости ее пола).

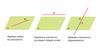
4.

Признак параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какойлибо прямой, лежащей в этой плоскости, то прямая и плоскость
параллельны (рисунок 29).
Доказательство:
Допустим, что b . Тогда по лемме о
пересечении плоскости параллельными
прямыми a (т.к. a b). Пришли к
противоречию с условием (a ),
b .

5.

Теорема 1. Если одна из двух пересекающихся плоскостей
содержит прямую, параллельную второй плоскости, то эта прямая
параллельна линии пересечения данных плоскостей (рисунок 30).
Доказательство:
Поскольку прямые a и l лежат в
одной плоскости , они либо
параллельны, либо пересекаются.
Если бы они пересекались,
прямая a имела бы общую точку с
плоскостью , что противоречит
условию.
Значит, a l.
Следствие: Если прямая a параллельна плоскости , то в этой плоскости
найдется бесконечно много прямых, параллельных a (через прямую a можно
провести бесконечно много плоскостей, каждая из которых будет пересекать
плоскость по прямой, параллельной a).

6.

Теорема 2. Если через каждую из двух параллельных прямых
проведена плоскость, и эти плоскости пересекаются, то линия
пересечения плоскостей параллельна каждой из этих прямых
(рисунок 31).
Доказательство:
1) a b ; по признаку
параллельности прямой и
плоскости a .
2) Плоскость содержит
прямую a, параллельную
плоскости , по теореме 1,
a l.
3) b a l, по теореме о
параллельности трех прямых,
b l.

7.

Теорема 3. Если прямая параллельна каждой из двух
пересекающихся плоскостей, то она параллельна линии их
пересечения (рисунок 32).
Доказательство:
1) с ; по следствию из
утверждения 1, в плоскости
найдется прямая a, параллельная c
(рисунок 32). Аналогично b :
с b.
2) a с b, по теореме о
параллельности трех прямых,
a b.
3) a b, a , b , = l,
по теореме 2, a l b.
4) c a l, по теореме о
параллельности трех прямых, с l.