2_2 СкалярВектСмеш24

1.

§ 4. Скалярное, векторное, смешанное
произведение векторов
Скалярное произведение
Опр. 1. Скалярным произведением векторов a и b
называется число (скаляр), равное произведению длин этих
векторов на косинус угла (a; b) между ними:
a b a b cos .
Обозначается: a b или ( a, b).
Свойства скалярного произведения.
1. a b b a.
6. a b 0
2. a b a пр a b b прb a.
3. a (b c) a b a c.
7. i i j j k k 1;
i j i k j k 0.
4. ( a ) b a ( b) (a b) ( – число).
2
5. a a a .
a b.

2.

Пример 1. Найдем длину вектора p 3a 4b, если a 2, b 3,
(a; b) .
3
p
p p.
p p (3a 4b) (3a 4b) 9a a 12a b 12b a 16b b
2
9a a 24a b 16b b 9 a 24 a b cos 16 b
3
2
1
9 2 24 2 3 16 32 36 72 144 108.
2
2
p 108 6 3.
2
a a a .
a (b c) a b a c.
a b b a.
a b a b cos .

3.

Выражение скалярного произведения через координаты
сомножителей
a xa ; ya ; za ; b xb ; yb ; zb ,
т. е. a xa i ya j za k ; b xb i yb j zb k .
a b ( xa i ya j za k ) ( xb i yb j zb k ) xa xb i i xa yb i j
xa zb i k ya xb j i ya yb j j ya zb j k za xb k i za yb k j
za zb k k xa xb 1 xa yb 0 xa zb 0 ya xb 0 ya yb 1
ya zb 0 za xb 0 za yb 0 za zb 1 xa xb ya yb za zb .
Итак, скалярное произведение двух векторов равно сумме
произведений одноименных декартовых координат этих
векторов:
a b xa xb ya yb za zb .

4.

Геометрические и физические приложения скалярного
произведения
1. Косинус угла между векторами
2. Длина вектора
cos(a; b)
3. Проекция вектора на вектор
.
a b
a a a.
прb a
a b
a b
.
b
4. Условие ортогональности двух векторов:
a b 0.
5. Работа постоянной по величине и направлению силы F
при перемещении материальной точки на вектор s равна
скалярному произведению силы и перемещения:
A F s
(физический смысл скалярного произведения).

5.

Пример
2.
Даны
координаты
вершин
A
треугольника A(3; –2; 6), B(2; 3; –1), C(4; 6; –7).
Найдем угол АBC.
cos ABC
BA BC
B
C
.
BA BC
BA 3 2; 2 3; 6 1 1; 5; 7 ;
BA
12 ( 5) 2 7 2 5 3;
2
2
2
BC 4 2; 6 3; 7 1 2; 3; 6 ; BC 2 3 ( 6) 7.
BA BC 1 2 ( 5) 3 7 ( 6) 2 15 42 55,
55
11 3
cos ABC
;
21
5 3 7
11 3
11 3
.
ABC arccos
arccos
21
21

6.

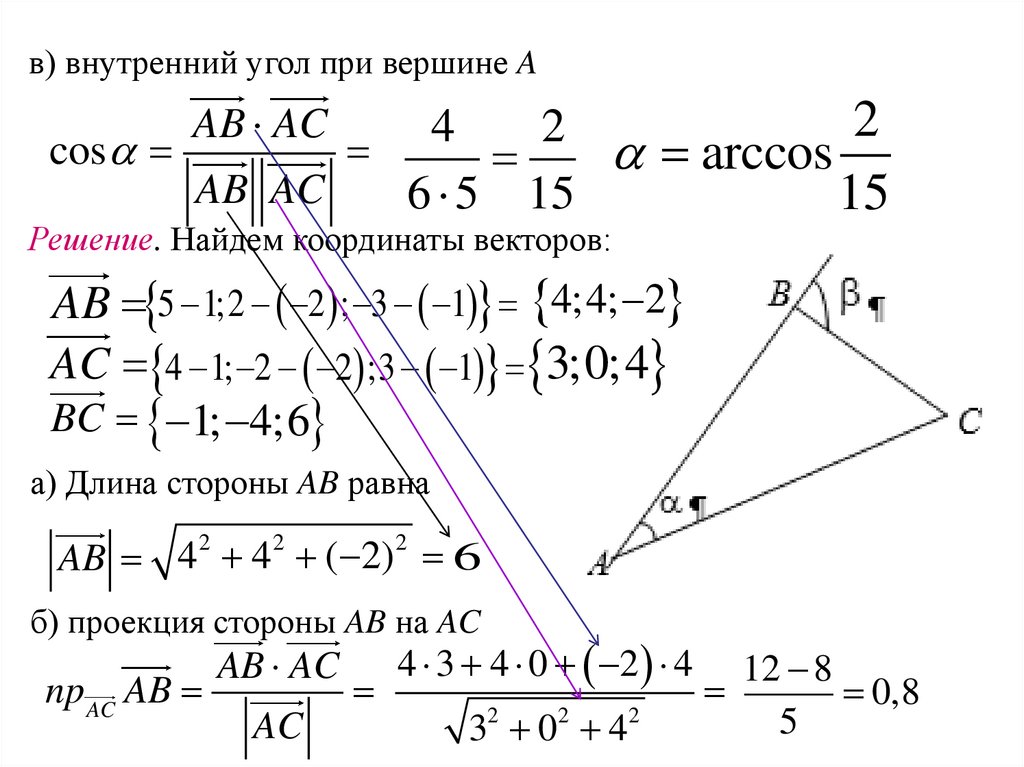
Пример. Даны координаты вершин треугольника ABC: A(1;-2;-1),
B(5;2;-3), C(4;-2;3).
Найти: а) длину стороны AB; б) проекцию стороны AB на AC; в)
внутренний угол при вершине A; г) внешний угол при вершине B.
Решение. Найдем координаты векторов:
AB 5 1;2 2 ; 3 1 4;4; 2
AC 4 1; 2 2 ;3 1 3;0;4
BC 1; 4;6
а) Длина стороны AB равна
2
2
2
4
4
(
2)
6
AB
б) проекция стороны AB на AC
np AC AB
AB AC
AC
4 3 4 0 2 4
32 02 42
12 8
0,8
5

7.

в) внутренний угол при вершине A
AB AC
2
4
2
cos
arccos
AB AC
6 5 15
15
Решение. Найдем координаты векторов:
AB 5 1;2 2 ; 3 1 4;4; 2
AC 4 1; 2 2 ;3 1 3;0;4
BC 1; 4;6
а) Длина стороны AB равна
2
2
2
4
4
(
2)
6
AB
б) проекция стороны AB на AC
np AC AB
AB AC
AC
4 3 4 0 2 4
32 02 42
12 8
0,8
5

8.

в) внутренний угол при вершине A
AB AC
2
4
2
cos
arccos
AB AC
6 5 15
15
AB 5 1;2 2 ; 3 1 4;4; 2
AC 4 1; 2 2 ;3 1 3;0;4
BC 1; 4;6
г) внешний угол β при вершине B, равен
CBA
cos CBA
BA BC
BA BC
4 ( 1) 4 ( 4) 2 6
6 ( 1) 2 ( 4) 2 62
BA 4; 4;2
32
, arccos 16
6 53
3 53

9.

Пример. Вычислите работу силы F 2i 3 j k
при
прямолинейном перемещении материальной точки из
положения А(-2;3;5) в положение B(3;0;-1).
Решение. Найдём координаты вектора AB
AB 3 2 ;0 3; 1 5 5; 3; 6
Тогда работа
A F AB 2 5 3 3 1 6 7
Пример. Найдите значение α, при котором векторы b 3;5;3 и
a 2 11; 6;3 1 перпендикулярны.
Решение. Условие перпендикулярности векторов a b 0
2 11 3 6 5 3 1 3 0
6 33 5 30 9 3 0
20 60
3

10.

Векторное произведение
Опр. 2. Векторным произведением вектора a на b вектор
называется вектор c a b, обладающий свойствами:
1) c a b sin(a; b)
(длина вектора c равна площади
параллелограмма, построенного на векторах a и b );
2) c a, c b;
3) векторы a, b, c
тройку.
в указанном порядке образуют правую
Обозначается: a b или [ a, b].

11.

Векторное произведение
Опр. 2. Векторным произведением вектора a на b вектор
называется вектор c a b, обладающий свойствами:
1) c a b sin(a; b)
(длина вектора c равна площади
параллелограмма, построенного на векторах a и b );
2) c a, c b;
3) векторы a, b, c
тройку.
в указанном порядке образуют правую
Обозначается: a b или [ a, b].
Свойства векторного произведения.
1. a b b a.
4. ( a) b a ( b) (a b)
( – число).
2. a (b c) a b a c. 5. a b 0 a b.
3. a a 0.
6. i i j j k k 0;
i j k ; j k i; k i j.

12.

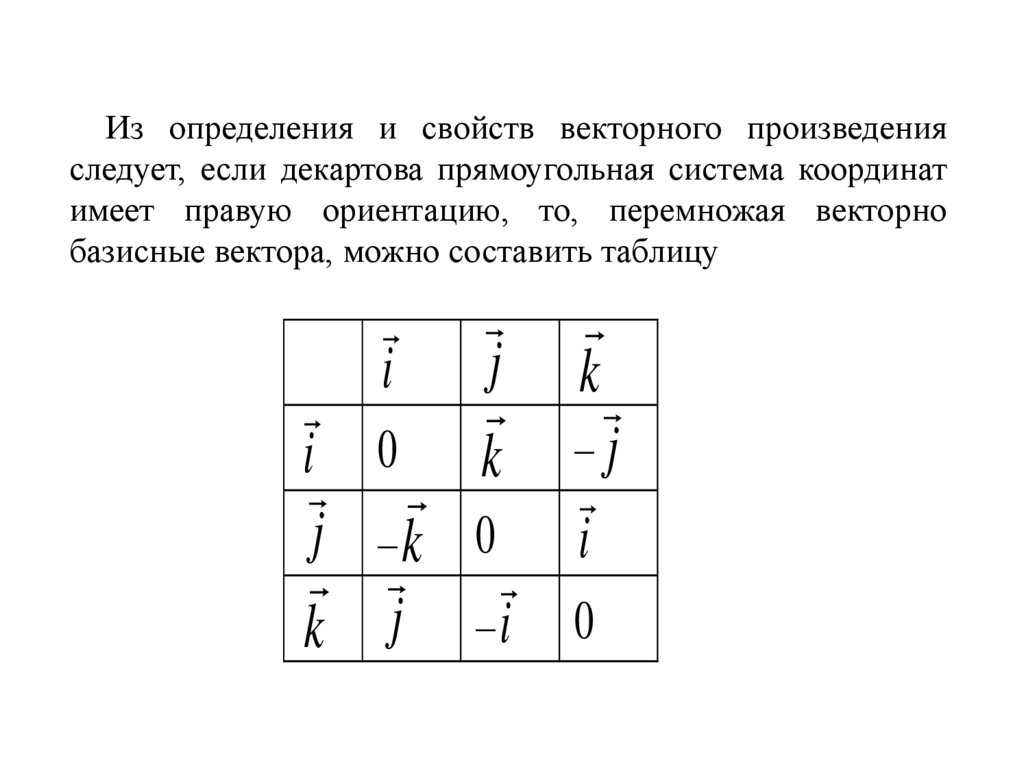
Из определения и свойств векторного произведения
следует, если декартова прямоугольная система координат
имеет правую ориентацию, то, перемножая векторно
базисные вектора, можно составить таблицу
i
j
k
i 0 k ‒j
j ‒k 0 i
k j ‒i 0

13.

Выражение векторного произведения через координаты
сомножителей
a xa ; ya ; za ; b xb ; yb ; zb ,
т. е. a xa i ya j za k ; b xb i yb j zb k .
a b ( xa i ya j za k ) ( xb i yb j zb k ) xa xb i i xa yb i j
xa zb i k ya xb j i ya yb j j ya zb j k za xb k i za yb k j
za zb k k xa xb 0 xa yb k xa zb ( j ) ya xb ( k ) ya yb 0
ya zb i za xb j za yb ( i ) za zb 0 i ( ya zb za yb ) j ( xa zb za xb )
ya
k ( xa yb ya xb ) i
yb
za
xa
j
zb
xb
za
xa
k
zb
xb
i
a b xa
j
ya
k
za .
xb
yb
zb
ya
i
yb
xa
j
ya
k
za .
xb
yb
zb

14.

Итак, векторное произведение двух векторов может быть
вычислено как формальный определитель, в первой строке
которого стоят базисные векторы i, j , k ,
а во второй и
третьей – декартовы координаты соответственно первого и
второго перемножаемых векторов:
i
a b xa
j
ya
k
za .
xb
yb
zb

15.

Геометрические и физические приложения векторного
произведения
1. Площадь параллелограмма, построенного на векторах a
и b , равна
S a b .
b
a
2. Площадь треугольника, построенного на векторах a и b
равна
1
S a b .
2
3. Момент силы F , приложенной в точке A, относительно
точки О равен
M O OA F .

16.

Пример 3. Найдем площадь
А(0; –1; 3), B(0; –2; 4), C(1; 0; 4).
треугольника
AB 0 0; 2 1; 4 3 0; 1;1 ;
AC 1 0; 0 1; 4 3 1;1;1 .
1
S AB AC .
A
2
i j k
0 1
0 1
1 1
AB AC 0 1 1 i
k
j
1 1
1 1
1 1
1 1 1
АBC,
если
B
D
i ( 1 1) j (0 1) k (0 1) 2i j k ;
AB AC ( 2) 2 12 12 6.
1
S
6.
2
Упражнение. В примере 3 найти длину высоты BD.
C

17.

Пример. Найти единичный вектор, перпендикулярный векторам
a 4;1;3 и b 4;0;2
Решение.
Вектор
c a b будет перпендикулярен векторам a и b
i j k
1
c 4 1 3 i
0
4 0 2
4
4 3
3
j
k
4 2
2
4
1
0
c 2i 4 j 4k
c 22 42 ( 4) 2 6.
1
1 2 2 e 1 c 1 ; 2 ; 2
e1 c ; ; 2
6
3 3 3
6
3 3 3

18.

Смешанное произведение трех векторов
Опр. 3. Смешанным произведением векторов a, b, c
называется число, равное скалярному произведению вектора a b
на вектор с :
abc (a b) c.
Замечание. В смешанном произведении abc (a b) c
сначала первый вектор a умножается векторно на второй b, а
затем полученный результат скалярно умножается на третий
вектор c.
Обозначают
abc
или
(a, b, c).

19.

Выражение смешанного произведения через координаты
сомножителей
a xa ; ya ; za ; b xb ; yb ; zb ; c xc ; yc ; zc .
i
abc (a b) c xa
xb
ya
i
yb
xc
za
xa
j
zb
xb
ya
za
yb
zb
yc
j
ya
yb
k
za ( xc i yc j zc k )
zb
za
xa
k
zb
xb
xa
za
xb
zb
zc
xa
abc xb
xc
xa
xb
ya
yb
yc
ya
( xc i yc j zc k )
yb
xa
ya
xb
yb
xc
za
zb .
zc
ya
yb
yc
za
zb .
zc

20.

Таким образом, смешанное произведение равно
определителю третьего порядка, в строках которого стоят
соответствующие координаты перемножаемых векторов.
xa
abc xb
xc
ya
yb
yc
za
zb .
zc

21.

Свойства смешанного произведения
1. Смешанное произведение не зависит от группировки
множителей: (a b) c a (b c).
2. Смешанное произведение не меняется при
циклической перестановке его множителей, и меняет знак
при перемене мест любых двух его множителей:
abc bca cab acb cba bac.
3. (a1 a2 )bc a1bc a2 bc.
4. ( a )bc (abc) ( – число).
5.
6.

22.

Геометрический смысл смешанного произведения:
Vпарал abc .
Vпарал Sоснh, Sосн a b . Обозначим (a b; c).
с
Если a, b, c образуют левую тройку, то
h c sin( 90 ) c cos .
a b
Если a, b, c образуют правую тройку, то
Vпарал Sосн h a b c cos (a b) c abc.
Vпарал abc . ◄
с h
a b φ b
а
Следовательно, объем пирамиды,
построенной на векторах a, b, c , равен
1
Vпир abc .
6
с
а
φb
Vпарал Sосн h a b c cos (a b) c abc.
h c sin(90 ) c cos .
h
b
а

23.

Свойства смешанного произведения
1. Смешанное произведение не зависит от группировки
множителей: (a b) c a (b c).
2. Смешанное произведение не меняется при
циклической перестановке его множителей, и меняет знак
при перемене мест любых двух его множителей:
abc bca cab acb cba bac.
3. (a1 a2 )bc a1bc a2 bc.
4. ( a )bc (abc) ( – число).
5. abc 0
6. abc 0
abc 0
a, b, c компланарны.
a, b, c образуют правую тройку;
a, b, c образуют левую тройку.

24.

Пример 4. Проверим, лежат ли точки
A(0; 1; 0), B(2; 4; –1), C(1; 0; 3), D(1; 10; –11) в
одной плоскости.
AB, AC , AD
лежат в одной плоскости,
т. е. компланарны.
C
A
D
B
AB 2 0; 4 1; 1 0 2; 3; 1 ;
AC 1 0; 0 1; 3 0 1; 1; 3 ;
AD 1 0;10 1; 11 0 1; 9; 11 .
2 3 1
1 1
1 3
1 3
( AB, AC , AD) 1 1 3 2 9 11 3 1 11 1 1 9
1 9 11
2 (11 27) 3 ( 11 3) 1 (9 1) 32 42 10 0.
AB, AC , AD
Компланарны.
Точки A, B, C, D лежат
в одной плоскости.

25.

Пример 5. Докажем, что векторы a i 3 j 2k , b 2i 4 j, c i 3 j 8k
образуют базис в пространстве.
1 3 2
2 4
4 0
2 0
abc 2 4 0 1
3
2
3 8
1 8
1 3
1 3 8
1 ( 32 0) 3 ( 16 0) 2 ( 6 4) 32 48 20 60 0.
a, b, c не компланарны
образуют базис в
пространстве.

26.

Взаимное расположение векторов
Рассмотрим три ненулевые вектора
a xa ; ya ; za ; b xb ; yb ; zb ; c xc ; yc ; zc .
1. Условие параллельности двух векторов.
Если два вектора параллельны, то их соответствующие
координаты пропорциональны: xa ya za
xb yb zb
2. Условие перпендикулярности двух векторов.
перпендикулярны, то их скалярное произведение равно
нулю:
x x y y z z 0.
a
b
a
b
a
b
3. Косинус угла между векторами
cosφ
xa xb ya yb za zb
a b
.

27.

4. Условие линейной независимости трех векторов.
Три вектора линейно независимы, если
xa
xb
xc
ya
yb
yc
za
zb 0.
zc