Презентация. Алгоритмы поиска

1. АЛГОРИТМЫ ПОИСКА

Разработчик: канд. физ.-мат. наук., доцент
Шевченко Алеся Сергеевна

2. ПЛАН:

1 Введение.
2 Линейный поиск.
3 Бинарный поиск.
2

3. 1 ВВЕДЕНИЕ

Задача поиска привлекала большое внимание ученых
(программистов) еще на заре компьютерной эры.
С 50-х годов началось решение проблемы поиска элементов,
обладающих определенным свойством в заданном множестве.
Алгоритмам поиска посвятили свои труды J. von Neumann, K.E.
Batcher, J. W. J. Williams, R.W. Floyd, R. Sedgewick, E. J. Isaac, C. A.
R. Hoare, D. E. Knuth, R. C. Singleton, D. L. Shell и другие.
3

4. 1 ВВЕДЕНИЕ

Задачу поиска можно сформулировать так: найти один или
несколько элементов в множестве, причем искомые элементы
должны обладать определенным свойством. Это свойство может
быть абсолютным или относительным.
Относительное свойство характеризует элемент по отношению
к другим элементам, например минимальный элемент в множестве
чисел.
Пример задачи поиска элемента с абсолютным свойством:
найти в конечном множестве пронумерованных элементов элемент с
номером 13, если такой существует
Все алгоритмы поиска разбиваются на две большие группы в
зависимости от того, упорядочен или нет массив данных, в котором
проводится поиск.
4

5. 2 ЛИНЕЙНЫЙ ПОИСК

Самый простой способ поиска, которым мы, сами того не
замечая, регулярно пользуемся в повседневной жизни, – линейный
поиск. Стартуя с начала (левый конец) массива, поочередно
сравниваем текущий элемент массива с нужным нам элементом x,
пока не найдем его.
5

6. 2 ЛИНЕЙНЫЙ ПОИСК

Свойства линейного поиска:
Временная сложность линейного поиска в наихудшем случае
равна O(n), где n – размер массива.
Пространственная сложность равна O(1), поскольку для
выполнения линейного поиска требуется постоянный объем памяти.
Реализация: линейный поиск можно легко реализовать с
помощью цикла, при котором каждая итерация сравнивает целевое
значение с текущим элементом массива.
Линейный поиск эффективен для небольших наборов данных,
но становится неэффективным для больших наборов данных. На
практике линейный поиск часто используется как подпрограмма в
более сложных алгоритмах.
6

7. 2 ЛИНЕЙНЫЙ ПОИСК

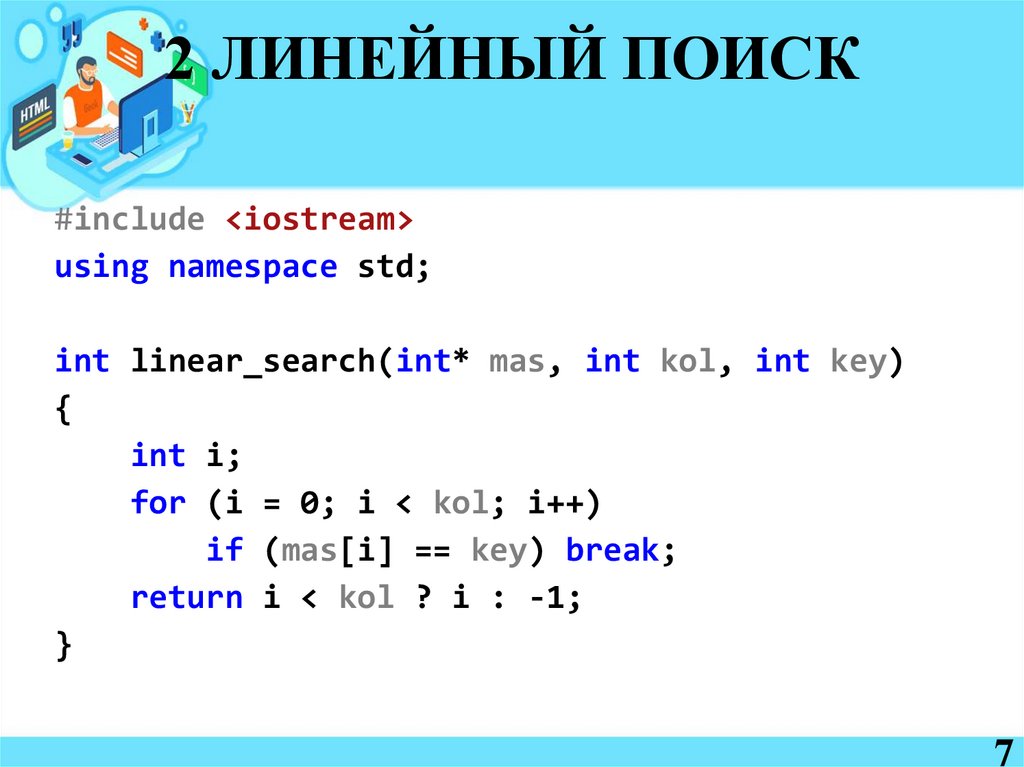
#include <iostream>
using namespace std;
int linear_search(int* mas, int kol, int key)
{
int i;
for (i = 0; i < kol; i++)
if (mas[i] == key) break;
return i < kol ? i : -1;
}
7

8. 2 ЛИНЕЙНЫЙ ПОИСК

int main()
{ int n, x;
cout << "Введите размер массива n= "; cin >> n;
int mas[n];
cout << "Введите элементы массива в строку = ";
for (int i = 0; i < n; i++) cin >> mas[i];
cout << "Введите элемент для поиска = ";
cin >> x;
int l = linear_search(mas, n, x);
if (l == -1) cout << "Такого элемента не
существует";
else cout << linear_search(mas, n, x);
return 0;
}
8

9. 2 ЛИНЕЙНЫЙ ПОИСК

Вопросы:
1.Выберите верные утверждения.
а)Линейный поиск элемента x = 3 в списке [1, 5, 4, 12, 3, 6] с
циклом for произведет четыре операции сравнения на равенство
(операция ==).
б)Число операций сравнения на равенство при линейном поиске
циклом for не может быть больше n-1, где n — длина массива.
в)Число операций сравнения на равенство при линейном поиске
циклом for не может быть больше длины массива.
д)Число операций сравнения на равенство при линейном поиске
циклом for не может быть меньше одного.
9

10. 2 ЛИНЕЙНЫЙ ПОИСК

2 Выберите верные утверждения.
а)Линейный поиск числа 8 в списке [1, 4, 2, 9, 8, 17, -5] выведет
число 4.
б)Если искомого элемента в списке нет, линейный поиск с
циклом for не запустится.
в)Линейный поиск возвращает индекс первого (если считать
слева) вхождения элемента x в список.
г)Линейный поиск работает только на отсортированных
массивах.
10

11. 3 БИНАРНЫЙ ПОИСК

Алгоритм линейного поиска, несмотря на свою простоту и
способность работы на неотсортированных массивах, не самый
эффективный алгоритм поиска. Он имеет временную сложность
O(n). Такая временная сложность (или асимптотика) говорит о том,
что в худшем варианте алгоритм пройдет по всему массиву.
Существует ли алгоритм с меньшей временной сложностью?
Да, но он будет работать только на отсортированных массивах.
Такой алгоритм называется бинарным поиском (реже его
называют двоичным поиском).
11

12. 3 БИНАРНЫЙ ПОИСК

Свойства бинарного поиска:
Временная сложность бинарного поиска в наихудшем случае
равна O(log(n)), где n – размер массива.
Пространственная сложность равна O(1), поскольку для
выполнения поиска требуется постоянный объем памяти.
12

13. 3 БИНАРНЫЙ ПОИСК

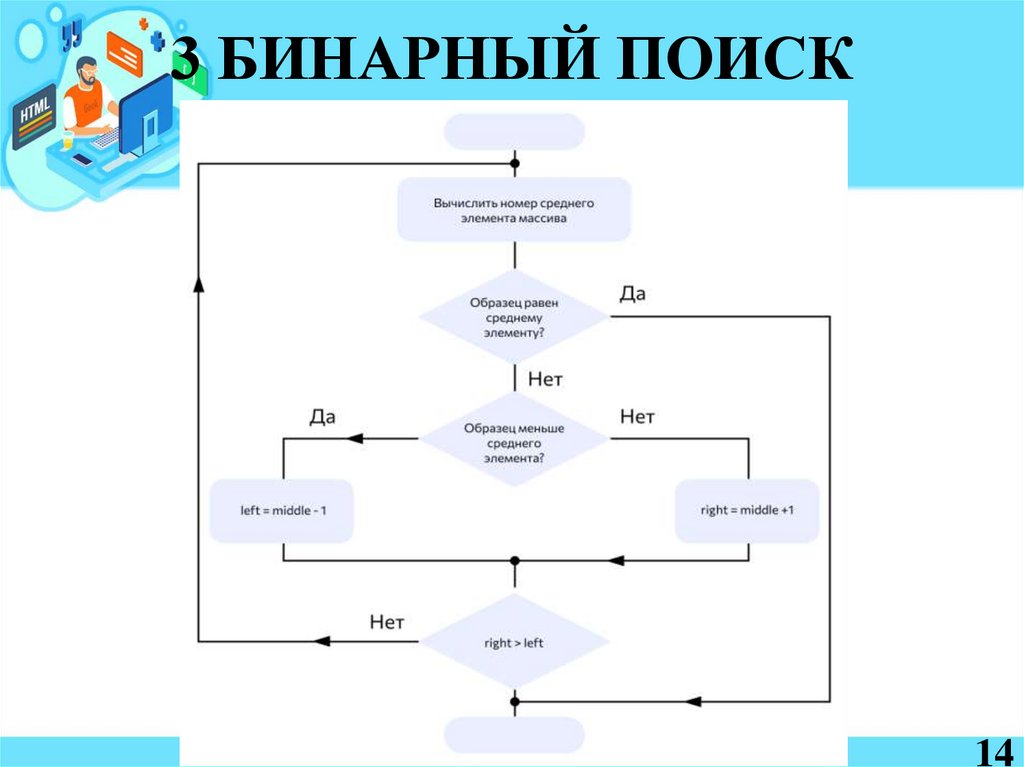
Основная последовательность действий алгоритма выглядит так:
1.Сортируем массив данных.
2.Делим его пополам и находим середину.
3.Сравниваем срединный элемент с заданным искомым
элементом.
4.Если искомое число больше среднего – продолжаем поиск в
правой части массива (если он отсортирован по возрастанию):
делим ее пополам, повторяя пункт 3. Если же заданное число
меньше – алгоритм продолжит поиск в левой части массива, снова
возвращаясь к пункту 3.
13

14. 3 БИНАРНЫЙ ПОИСК

14

15. 3 БИНАРНЫЙ ПОИСК

15

16. 3 БИНАРНЫЙ ПОИСК

#include <iostream>
using namespace std;
int BinarySearch(int* x, int k, int key)
{ bool found = false;
int left = 0, right = k - 1;
int middle = (right + left) / 2;
while (!found && right >= left)
{
if (key == x[middle]) found = true;
else if (key < x[middle]) right=middle - 1;
else left = middle + 1;
middle = (right + left) / 2;
}
return found ? middle : -1;
}
16

17. 3 БИНАРНЫЙ ПОИСК

На основе бинарного поиска разработано несколько
дополнительных разновидностей поисковых алгоритмов:
- однородный бинарный поиск, при котором аргумент поиска
А сравнивается с ключом Ki, где i – золотое сечение интервала
(оно выбирается так, чтобы отношение длины большего отрезка к
длине всего интервала равнялось отношению длины меньшего
отрезка к длине большего отрезка);
- троичный поиск, когда интервал делится на три части вместо
двух. Обычно применяется для поиска положения экстремума
функции;
17

18. 3 БИНАРНЫЙ ПОИСК

- интерполирующий поиск, который предсказывает позицию
нужного элемента на основе разницы значений. Эффективен, если
элементы распределены достаточно равномерно;
- дробный спуск – применяется для ускорения двоичного
поиска в многомерных массивах данных, и другие.
18

19. 3 БИНАРНЫЙ ПОИСК

Вопросы:
1. Обязательна ли сортировка списка перед запуском
бинарного поиска?
Нет
Да
2. Что из нижеперечисленного является недостатком
использования двоичного поиска?
Двоичный поиск можно использовать только в отсортированных
массивах.
Двоичный поиск имеет наихудшую временную сложность O(n).
Двоичный поиск требует много памяти.
Двоичный поиск не является точным.
19