Двумерные массивы

1.

СПбГУТ им. проф. М.А. Бонч–Бруевича
Кафедра программной инженерии и вычислительной техники (ПИ и ВТ)
ПРОГРАММИРОВАНИЕ
Единственный способ изучать новый язык
программирования – писать на нем программы.
Брайэн Керниган
Лекция 11: Двумерные массивы
1.
2.
3.
4.
5.
Двумерные массивы
Операции с двумерными массивами
Сортировка в массиве
Поиск в массиве
Связь двумерных массивов с указателями
Санкт–Петербург, 2021г.

2.

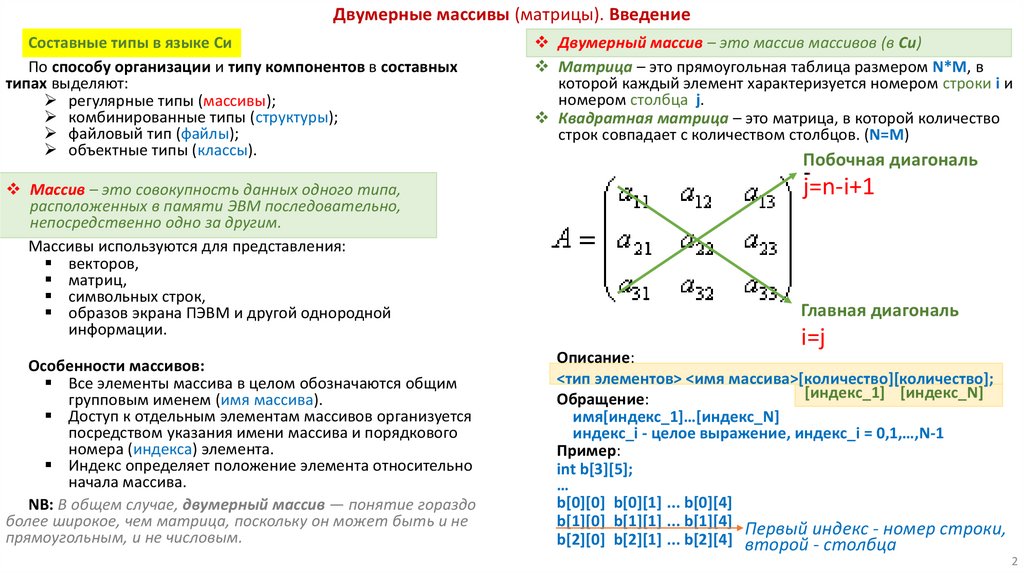
Двумерные массивы (матрицы). Введение
Составные типы в языке Си
По способу организации и типу компонентов в составных
типах выделяют:
регулярные типы (массивы);
комбинированные типы (структуры);
файловый тип (файлы);
объектные типы (классы).
Массив – это совокупность данных одного типа,
расположенных в памяти ЭВМ последовательно,
непосредственно одно за другим.
Массивы используются для представления:
векторов,
матриц,
символьных строк,
образов экрана ПЭВМ и другой однородной
информации.
Особенности массивов:
Все элементы массива в целом обозначаются общим
групповым именем (имя массива).
Доступ к отдельным элементам массивов организуется
посредством указания имени массива и порядкового
номера (индекса) элемента.
Индекс определяет положение элемента относительно
начала массива.
NB: В общем случае, двумерный массив — понятие гораздо
более широкое, чем матрица, поскольку он может быть и не
прямоугольным, и не числовым.
Двумерный массив – это массив массивов (в Си)
Матрица – это прямоугольная таблица размером N*M, в
которой каждый элемент характеризуется номером строки i и
номером столбца j.
Квадратная матрица – это матрица, в которой количество
строк совпадает с количеством столбцов. (N=M)
Побочная диагональ
j=n-i+1
Главная диагональ
i=j
Описание:
<тип элементов> <имя массива>[количество][количество];
[индекс_1] [индекс_N]
Обращение:
имя[индекс_1]…[индекс_N]
индекс_i - целое выражение, индекс_i = 0,1,…,N-1
Пример:
int b[3][5];
…
b[0][0] b[0][1] ... b[0][4]
b[1][0] b[1][1] ... b[1][4] Первый индекс - номер строки,
b[2][0] b[2][1] ... b[2][4] второй - столбца
2

3.

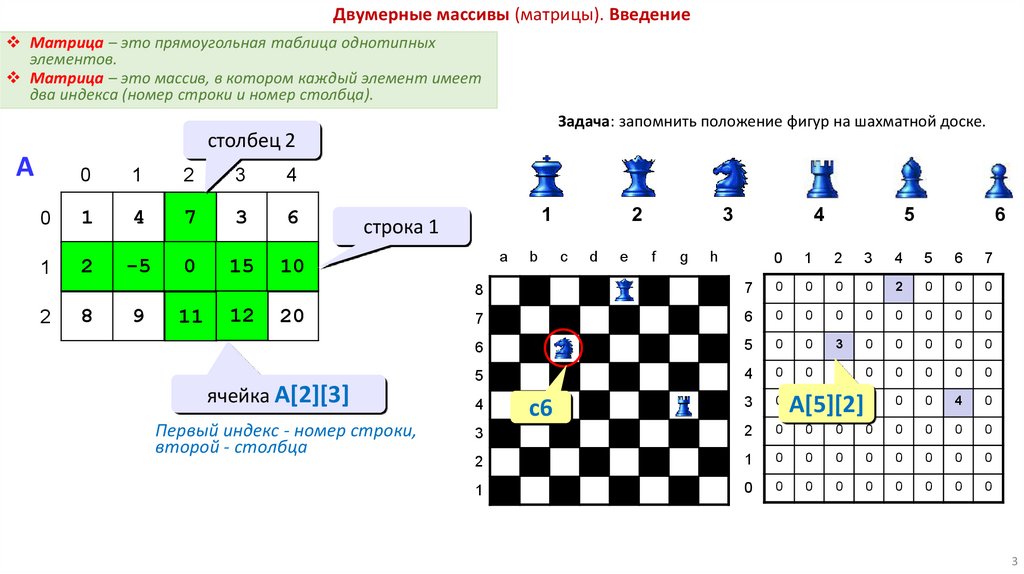
Двумерные массивы (матрицы). Введение
Матрица – это прямоугольная таблица однотипных
элементов.
Матрица – это массив, в котором каждый элемент имеет
два индекса (номер строки и номер столбца).
Задача: запомнить положение фигур на шахматной доске.
столбец 2
A
0
1
2
3
4
0
1
4
7
3
6
1
2
-5
0
15
10
2
8
9
11
12
1
строка 1
20
ячейка A[2][3]
Первый индекс - номер строки,
второй - столбца
a
b
2
c
d
e
3
f
g
4
h
5
6
0
1
2
3
4
5
6
7
8
7
0
0
0
0
2
0
0
0
7
6
0
0
0
0
0
0
0
0
6
5
0
0
3
0
0
0
0
0
5
4
0
0
0
0
0
0
0
0
3
0
0
0
0
A[5][2]
0
0
4
0
3
2
0
0
0
0
0
0
0
0
2
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
4
c6
3

4.

Двумерный массив. Применение
Использование двумерных массивов для построения поверхностей
4

5.

Двумерный массив. Применение
Псевдографика
5

6.

1. Двумерные массивы (Указатели на указатели)
В языке программирования Си предусматриваются
ситуации, когда указатели указывают на указатели.
Такие ситуации называются многоуровневой адресацией.
Пример объявления указателя на указатель:
int **ptr2;
В приведенном объявлении **ptr2 – это указатель на
указатель на число типа int.
При этом наличие **двух звездочек свидетельствует о том,
что имеется двухуровневая адресация.
Для получения значения конкретного числа следует
выполнить следующие действия:
int x = 88, *ptr, **ptr2;
ptr = &x;
ptr2 = &ptr;
printf("%d", **ptr2); /* 88 */
В результате в выходной поток (на дисплей пользователя)
будет выведено число 88.
В приведенном фрагменте переменная *ptr объявлена как
указатель на целое число, а **ptr2 – как указатель на
указатель на целое.
Значение, выводимое в выходной поток (число 88),
осуществляется операцией разыменования указателя **ptr2.
Для многомерных массивов указатели указывают на адреса
элементов массива построчно.
int **a
int *a[nstr]
a
a[0]
a[1]
int *a[nstr][nstb]
a[0][1]
0
a[1][0]
…
…
nstb-1
0
…
a[nstr-1]
…
Двумерный массив (матрица) – одномерный массив
одномерных массивов.
<>тип элементов> <имя массива [количество][количество];
Указывается количество элементов в одномерном массиве, а
потом указывается количество элементов в одномерных
массивах.
Схема выделения памяти под двумерный массив int A[20][5];
Элементами первого одномерного массива являются адреса,
а второго – целые значения.
6

7.

Двумерные массивы
Двумерный массив int a[3][4] можно представить в виде
таблицы:
a[0][0]
a[0][1]
a[0][2]
a[0][3]
a[1][0]
a[1][1]
a[1][2]
a[1][3]
a[2][0]
a[2][1]
a[2][2]
a[2][3]
Выделение памяти под матрицу:
Колич.байт =размер типа данных *колич. строк *колич.
столбцов
В памяти компьютера массив располагается непрерывно
по строкам, т. е.:
а[0][0], a[0][1], a[0][2], a[0][3],
а[1][0], а[1][1], а[1][2], а[1][3],
а[2][0], а[2][1], а[2][2], а[2][3].
Пример объявления двумерных массивов:
const int N=4, M=5;
int A[N][M], B[N][N];
float a[2][2] = {{3.2, 4.3}, {1.1, 2.2}};
char sym[2][2] = { 'a', 'b', 'c', 'd' };
Обращение к элементам массива:
A[0][3]=8; X[1][2]=0.678;
B[2][0]= A[0][3]*2;
Y[2][1]=Y[2][2]=5.5;
Для однородной обработки каждого элемента матрицы
используют вложенные циклы. Например:
//заполнение матрицы с помощью датчика случайных чисел
for (int i=0; i<N; i++)
//цикл по строкам
for ( int j=0; j<M ; j++) //цикл внутри строки по столбцам
A[i][j]=rand(50); // предварительно исп. srand(time(NULL));
//вывод матрицы на экран
for ( i=0; i<M; i++)
//цикл по строкам
{ for ( j=0; j<N ; j++)
//цикл внутри строки по столбцам
printf (“%5.1f “,Y[i][j] );
printf (“\n “ );
// переход на новую строку
}
const int M=6, N=5;
float Y[M][N];
int B[N][N];
//обнуление матрицы
for ( i=0; i<M; i++)
//цикл по строкам
for ( j=0; j<N ; j++) //цикл внутри строки по столбцам
Y[i][j]=0.0;
// заполнение единичной матрицы:
// элементы главной диагонали равны 1,
// все остальные элементы = 0
for ( i=0; i<N; i++)
//цикл по строкам
for ( j=0; j<N ; j++)
//цикл внутри строки по столбцам
if (i==j) B[i][j]=1; else B[i][j]=0;
7

8.

Двумерные массивы
Ввод с клавиатуры:
for ( i = 0; i < N; i ++ )
for ( j = 0; j < M; j ++ )
{
printf ( "A[%d][%d]=", i, j);
scanf ( "%d", &A[i][j] );
}
i
j
A[0][0]= 25
A[0][1]= 14
A[0][2]= 14
...
A[2][3]= 54
Заполнение случайными числами:
for ( i = 0; i < N; i ++ )
// цикл по строкам
for ( j = 0; j < M; j ++ )
// цикл по столбцам
A[i][j] = rand(25) - 10; // srand(time(NULL));
Вывод на экран:
for ( i = 0; i < N; i ++ )
{ for ( j = 0; j < M; j ++ ) // вывод строки
printf("%5d", A[i,j]); // в той же строке
printf("\n"); // перейти на новую строку
}
12
25
1
13
156
1
12
447
1
456
222
23
Обработка всех элементов массива (матрицы)
Пример: заполнить матрицу из 3 строк и 4 столбцов
случайными числами и вывести ее на экран. Найти сумму
элементов матрицы.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int random(int N) // функция выдает случайное число от 0 до N-1
{ srand(time(NULL)); // инициализация текущим временем rand()
return rand()%N;
}
int main()
{
const int N = 3, M = 4;
int A[N][M], i, j, S = 0;
/* Заполнение матрицы:*/
for ( i = 0; i < N; i ++ )
// цикл по строкам
for ( j = 0; j < M; j ++ ) // цикл по столбцам
A[i][j] = random(25) - 10;
/* Вывод на экран: */
for ( i = 0; i < N; i ++ )
for ( j = 0; j < M; j ++ )
S += A[i][j];
printf("Сумма элементов матрицы S=%d", S);
return 0;
}
8

9.

Двумерные массивы
Инициализация
При статической (определяемой на этапе компиляции)
инициализации значения массива перечисляются в порядке
указания размеров (индексов) в определении массива.
Каждый уровень (индекс), кроме самого младшего,
многомерного массива заключается в свою пару фигурных
скобок.
Значения самого младшего индекса указываются через
запятую:
const unsigned int DIM1 = 3; // dimmetion of memory
const unsigned int DIM2 = 5; // выделение памяти
int ary[DIM1][DIM2] =
{
{ 1, 2, 3, 4, 5 },
{ 2, 4, 6, 8, 10 },
{ 3, 6, 9, 12, 15 }
};
В примере показана статическая инициализация
прямоугольного массива.
Весь список инициализирующих значений заключён в
фигурные скобки.
Значения для каждой из 3 строк заключены в свою пару из
фигурных скобок, значения для каждого из 5 столбцов для
каждой строки перечислены через запятую.
При наличии инициализатора, самый левый размер массива
может быть опущен.
В этом случае компилятор сам определит этот размер, исходя
из списка инициализации.
Расположение в памяти
Для многомерного C-массива выделяется единый блок памяти
необходимого размера:
размер_массива1 * размер_массива2 * ... * размер_массиваN *
sizeof(тип_элемента_массива)
Для двумерного массива:
размер_массива1 * размер_массива2 * sizeof(тип_эл-та_массива)
Значения располагаются последовательно.
Самый левый индекс изменяется медленнее всего.
Т.е. для трёхмерного массива сначала располагаются значения
для первой (индекс 0) матрицы, затем для второй и т.д.
Значения для матриц располагаются построчно (ср. со
статической инициализацией массива выше).
Имя (идентификатор) многомерного C-массива является
указателем на первый элемент массива (так же как и для
одномерных массивов)
Из выводов, приведённых выше, следует, что работу с
двумерным или многомерным массивом (в понимании на
более высоком уровне абстракции) технически можно
организовать посредством одномерного массива
соответствующего размера.
Такой приём программирования достаточно распространён.
Его выгода в том, что массив ary[DIM1 * DIM2] не обязательно
должен быть выделен автоматически. Его можно выделять и
динамически (рассмотрим в соответствующей теме).
9

10.

2. Операции с двумерными массивами (матрицами)
Пример 1: Вывести на экран главную диагональ квадратной
матрицы из N строк и N столбцов.
for ( i = 0; i < N; i ++ )
printf ( "%5d", A[i][i] );
A[0][0]
A[1][1]
A[2][2]
Пример 3: Найти сумму элементов, стоящих на главной
диагонали и ниже ее.
строка 0: A[0][0]
строка 1: A[1][0]+A[1][1]
...
строка i: A[i][0]+A[i][2]+...+A[i][i]
A[N-1][N-1]
S = 0;
for ( i = 0; i < N; i ++ ) // цикл по всем строкам
for ( j = 0; j <= i; j ++ ) // складываем нужные элементы строки i
S += A[i][j];
Пример 2: Вывести на экран вторую (побочную) диагональ
Пример 4: Перестановка строк или столбцов. В матрице из
N строк и M столбцов переставить 1-ую и 3-ю строки.
A[0][N-1]
A[1][N-2]
A[N-2][1]
A[N-1][0]
for ( i = 0; i < N; i ++)
printf ( "%5d", A[i][ N-1-i ]);
j
for ( j = 0; j <= M; j ++ )
{
tmp = A[1][j];
A[1][j] = A[3][j];
A[3][j] = tmp;
}
A[1][j]
1
1
2
5
2
1
3
7
3
1
3
7
A[3][j]
10

11.

Операции с двумерными массивами (матрицами)
Пример 5: К третьему столбцу добавить значения шестого.
for ( i = 0; i < N; i ++ )
A[i][3] += A[i][6];
Пример 6: Каждому элементу массива присваиваем
значение произведения текущих индексов элементов массива.
#include <stdio.h>
int main()
{ const int N=8;
int i, j;
// объявляем массив размером 8*8 элементов:
int myArray[N][N];
for ( i = 0; i < N; i++ )
{
for ( j = 0; j < N; j++ )
myArray[i][j] = i * j; /* каждому элементу присваиваем
значение произведения текущих индексов элемента массива */
}
printf( "Вот такой массив у нас получился:\n" );
for ( i = 0; i < N; i++ )
{
for ( j = 0; j < N; j++ )
{
printf( "[%d][%d]=%d ", i, j, myArray[i][j] );
}
printf( "\n" );
}
getchar();
}
11

12.

Примеры алгоритмов обработки массивов
Заполнение массива случайными числами
Функция стандартной библиотеки языка Си: rand()
int rand(void); генерирует псевдослучайное на интервале
0..RAND_MAX (= 32767, но зависит от реализации языка).
Числа 0…9: rand()%10;
Последовательность псевдослучайная,
Числа 1…9: rand()%10 + 1; но всегда одинаковая !!!
// 1. Заполнение (построчно, слева направо)
for (int i = 0; i<n; i++)
for(int j = 0; j<m; j++)
a[i][j] = something;
i=1..n
j=1..m
Для исправления ситуации:
void srand (unsigned int seed); /* Установить
начальное значение последовательности */
time_t time (time_t* timer); // #include <time.h>
srand(time(NULL));
Заполнение массива случайными числами:
//от 1 до 10:
#include <time.h>
srand(time(NULL)); // берем текущее время
for (int i = 0; i < n; i++ ) A[i] = rand()%10+1;
//от -20 до 20:
srand(time(NULL));
for (int i = 0; i < n; i++ ) A[i] = rand() % 41-20;
//на отрезке от a до b:
srand(time(NULL)*1000);
for (int i=0; i<n; i++)
{
A[i]=(rand()*1.0/(RAND_MAX)*(b-a)+a);
}
i/j
0
1
2
3
0
(0,0)
(0,1)
(0,2)
(0,3)
1
(1,0)
(1,1)
(1,2)
(1,3)
2
(2,0)
(2,1)
(2,2)
(2,3)
3
(3,0)
(3,1)
(3,2)
(3,3)
4
(4,0)
(4,1)
(4,2)
(4,3)
// 2. Сумма всех элементов
int sum=0;
for (int i = 0; i<n; i++)
for(int j = 0; j<m; j++)
sum += a[i][j];
// 3. Сумма элементов строки
int sum=0;
for(int j = 0; j<m; j++)
sum += a[3][j];
// 4. Сумма элементов столбца
int sum=0;
for(int i = 0; i<n; i++)
sum += a[i][3];
// 5. Максимальный в каждом столбце
int max[4];
for(int j = 0; i<m; j++)
{
max[j]=max[j,0];
for(int i=1;i<n;i++)
if (a[i][j] > max[j]) max[j]=a[i][j];
}
12

13.

Примеры алгоритмов обработки массивов
Заполнение единицами
Ниже и на главной диагонали:
for (int i=0; i<n; i++)
for (int j=0; j<=i; j++) a[i][j]=1;
//Сумма элементов главной диагонали
for(int i = 0; i<n; i++) sum+=a[i][i];
//Сумма элементов выше главной диагонали
Выше и на главной диагонали:
for (int i=0; i<n; i++)
for (int j=i; j<n; j++) a[i][j]=1;
for(int i = 0; i<n; i++)
for(int j = 0; i<n; j++)
if (i < j) sum+=a[i][j];
//Сумма элементов побочной диагонали
for(int i = 0; i<n; i++) sum+=a[i][n-i-1];
Выше и на побочной диагонали:
for (int i=0; i<n; i++)
for (int j=0; j < n-i; j++) a[i][j]=1;
//Сумма элементов выше главной диагонали
for(int i = 0; i<n; i++)
for(int j = 0; i<n; j++)
if (i < j) sum+=a[i][j];
Ниже и на побочной диагонали:
for (int i=0; i<n; i++)
for (int j=(n-i-1); j < n; j++) a[i][j]=1;
13

14.

Особенности двумерных (многомерных) статических массивов
Особенностью является то, что по своему строению
многомерный массив является обыкновенным,
"одномерным", массивом:
Все элементы расположены друг за другом.
Доступ до элемента a[i][j] – по существу сдвиг на
i*число столбцов + j
В двумерном массиве, таким образом, элементы
расположены "по рядам", в трёхмерном - "по слоям", внутри
которых элементы расположены "по рядам" и т.д.
В связи с этим, при начальной инициализации опускать
размерность можно только в первых квадратных скобках:
int a[][3] = {0};
int b[][5][25] = {0};
Компилятор будет знать в таком случае сдвиг, необходимый
для доступа к элементу.
С этим связаны и особенности начальной инициализации.
Так как многомерный массив по сути одномерный, то его
начальную инициализацию можно провести так
int a[2][3] = {1, 2, 3, 4, 5, 6};
Можно опустить первую размерность:
int a[][2][3] = {1, 2, 3, 34, 5, 6, 7, 8, 9, 10, 11, 12};
Можно с помощью фигурных скобок сделать данные более
удобными для чтения:
int a[2][3] = {{1, 2, 3}, {4, 5, 6}}
или
int a[][3][4] =
{{{1, 2, 3, 4}, {2, 4, 6, 8}, {3, 6, 9, 12}},
{{1, 2, 3, 4}, {2, 4, 6, 8}, {3, 6, 9, 12}},
{{1, 2, 3, 4}, {2, 4, 6, 8}, {3, 6, 9, 12}}};
Также, как и в одномерных массивах, если заявлено данных
больше, чем указано при инициализации, то оставшиеся
заполняются нулями.
Например, единичная матрица 3 на 3:
int zero3[3][3] = {{1}, {0, 1}, {0, 0, 1}};
Из того, что многомерный массив является одномерным по
структуре, вытекают некоторые интересные свойства.
Например, доступ до элемента может быть осуществлён
через его порядковый номер:
a[i][j] === a[0][i*число столбцов + j] и т.д.
Количество размерностей массива практически не
ограничено:
int a[3][2];
Компилятор Си располагает строки матрицы a в памяти
одну за другой вплотную друг к другу:
a[0][0]
a[0][1]
a[1][0]
a[1][1]
a[2][0]
a[2][1]
printf(“%d”, a[2][0]); // не a[2,0] как в Pascal
14

15.

Особенности двумерных (многомерных) статических массивов
Компоненты многомерного массива int a[2][3][5];
a – массив из двух элементов типа “int [3][5]”
int (*p)[3][5] = a;
a[i] – массив из трех элементов типа “int [5]” (i [0, 1])
int (*q)[5] = a[i];
a[i][j] – массив из пяти элементов типа “int” (i [0, 1], j [0, 1, 2])
int *r = a[i][j];
a[i][j][k] – элемент типа “int” (i [0, 1], j [0, 1, 2], k [0, 1, 2, 3, 4])
int s = a[i][j][k];
15

16.

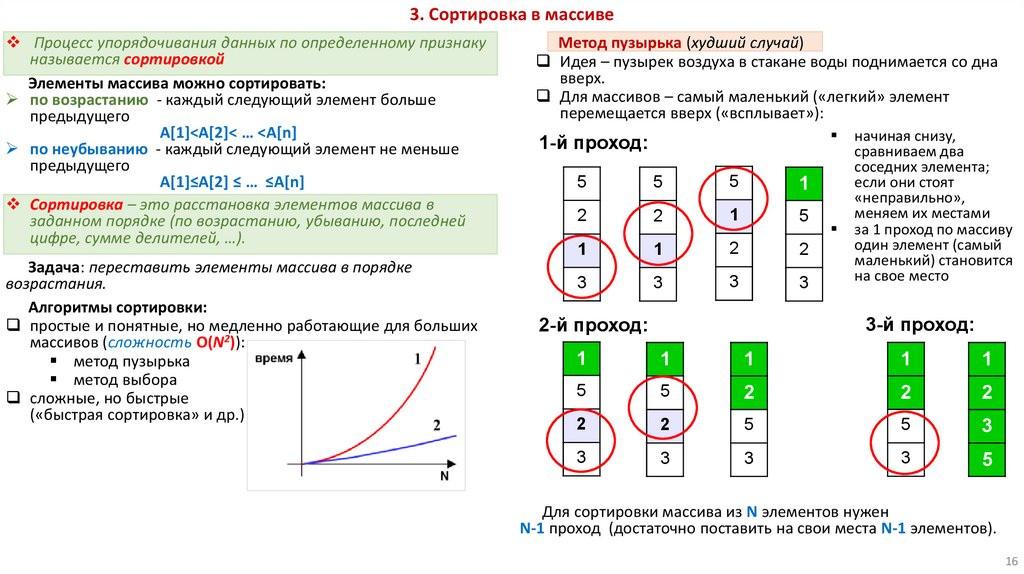
3. Сортировка в массиве
Процесс упорядочивания данных по определенному признаку
называется сортировкой
Элементы массива можно сортировать:
по возрастанию - каждый следующий элемент больше
предыдущего
A[1]<A[2]< … <A[n]
по неубыванию - каждый следующий элемент не меньше
предыдущего
A[1]≤A[2] ≤ … ≤A[n]
Сортировка – это расстановка элементов массива в
заданном порядке (по возрастанию, убыванию, последней
цифре, сумме делителей, …).
Задача: переставить элементы массива в порядке
возрастания.
Алгоритмы сортировки:
простые и понятные, но медленно работающие для больших
массивов (сложность O(N2)):
метод пузырька
метод выбора
сложные, но быстрые
(«быстрая сортировка» и др.)
Метод пузырька (худший случай)
Идея – пузырек воздуха в стакане воды поднимается со дна
вверх.
Для массивов – самый маленький («легкий» элемент
перемещается вверх («всплывает»):
1-й проход:
5
5
5
1
2
2
1
5
1
1
2
2
3
3
3
3
начиная снизу,
сравниваем два
соседних элемента;
если они стоят
«неправильно»,
меняем их местами
за 1 проход по массиву
один элемент (самый
маленький) становится
на свое место
3-й проход:
2-й проход:
1
1
1
1
1
5
5
2
2
2
2
2
5
5
3
3
3
3
3
5
Для сортировки массива из N элементов нужен
N-1 проход (достаточно поставить на свои места N-1 элементов).
16

17.

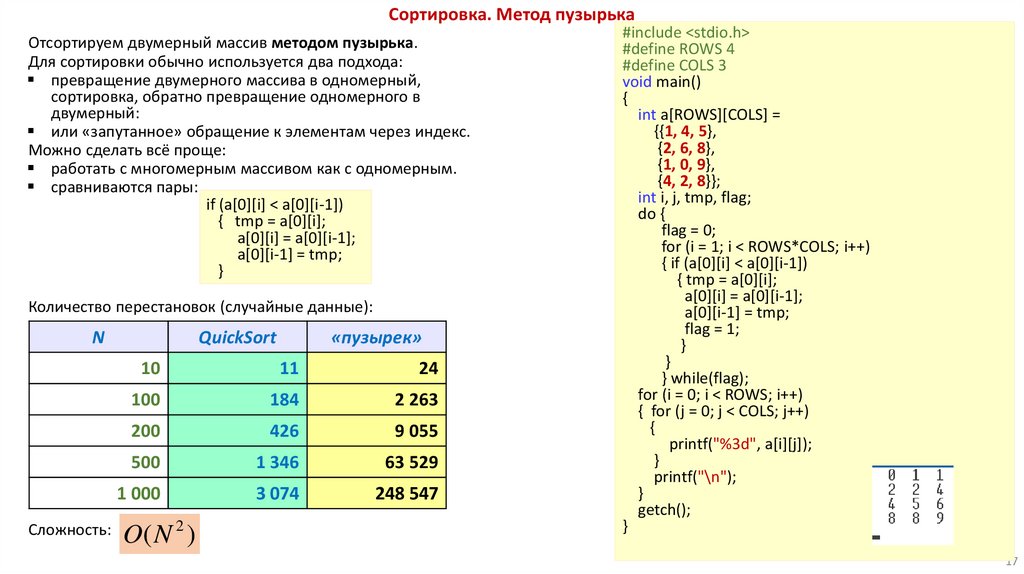
Сортировка. Метод пузырька
Отсортируем двумерный массив методом пузырька.
Для сортировки обычно используется два подхода:
превращение двумерного массива в одномерный,
сортировка, обратно превращение одномерного в
двумерный:
или «запутанное» обращение к элементам через индекс.
Можно сделать всё проще:
работать с многомерным массивом как с одномерным.
сравниваются пары:
if (a[0][i] < a[0][i-1])
{ tmp = a[0][i];
a[0][i] = a[0][i-1];
a[0][i-1] = tmp;
}
Количество перестановок (случайные данные):
N
QuickSort
«пузырек»
10
11
24
100
184
2 263
200
426
9 055
500
1 346
63 529
1 000
3 074
248 547
Сложность: O( N 2 )
#include <stdio.h>
#define ROWS 4
#define COLS 3
void main()
{
int a[ROWS][COLS] =
{{1, 4, 5},
{2, 6, 8},
{1, 0, 9},
{4, 2, 8}};
int i, j, tmp, flag;
do {
flag = 0;
for (i = 1; i < ROWS*COLS; i++)
{ if (a[0][i] < a[0][i-1])
{ tmp = a[0][i];
a[0][i] = a[0][i-1];
a[0][i-1] = tmp;
flag = 1;
}
}
} while(flag);
for (i = 0; i < ROWS; i++)
{ for (j = 0; j < COLS; j++)
{
printf("%3d", a[i][j]);
}
printf("\n");
}
getch();
}
17

18.

Быстрая сортировка
Быстрая сортировка представляет собой
усовершенствованный метод сортировки, основанный на
принципе обмена.
Пузырьковая сортировка является самой неэффективной из
всех алгоритмов прямой сортировки.
Однако усовершенствованный алгоритм является лучшим из
известных методом сортировки массивов.
Он обладает столь блестящими характеристиками, что его
изобретатель Ч. Хоар назвал его быстрой сортировкой.
Для достижения наибольшей эффективности желательно
производить обмен элементов на больших расстояниях.
В массиве выбирается некоторый элемент, называемый
разрешающим.
Затем он помещается в то место массива, где ему полагается
быть после упорядочивания всех элементов.
В процессе отыскания подходящего места для разрешающего
элемента производятся перестановки элементов так, что
слева от них находятся элементы, меньшие разрешающего, и
справа — большие (предполагается, что массив сортируется
по возрастанию).
Тем самым массив разбивается на две части:
не отсортированные элементы слева от разрешающего
элемента;
не отсортированные элементы справа от разрешающего
элемента.
Чтобы отсортировать эти два меньших подмассива, алгоритм
рекурсивно вызывает сам себя.
Если требуется сортировать больше одного элемента, то
нужно:
выбрать в массиве разрешающий элемент;
переупорядочить массив, помещая элемент на его
окончательное место;
отсортировать рекурсивно элементы слева от
разрешающего;
отсортировать рекурсивно элементы справа от
разрешающего.
Ключевым элементом быстрой сортировки является алгоритм
переупорядочения.
Пример: Рассмотрим сортировку на массиве:
10, 4, 2, 14, 67, 2, 11, 33, 1, 15.
Для реализации алгоритма переупорядочения используем
указатель left на крайний левый элемент массива.
Указатель движется вправо, пока элементы, на которые он
показывает, остаются меньше разрешающего.
Указатель right поставим на крайний правый элемент
массива, и он движется влево, пока элементы, на которые он
показывает, остаются больше разрешающего.
Пусть крайний левый элемент — разрешающий pivot.
Установим указатель left на следующий за ним элемент; right
— на последний.
Алгоритм должен определить правильное положение
элемента 10 и по ходу дела поменять местами неправильно
расположенные элементы.
18

19.

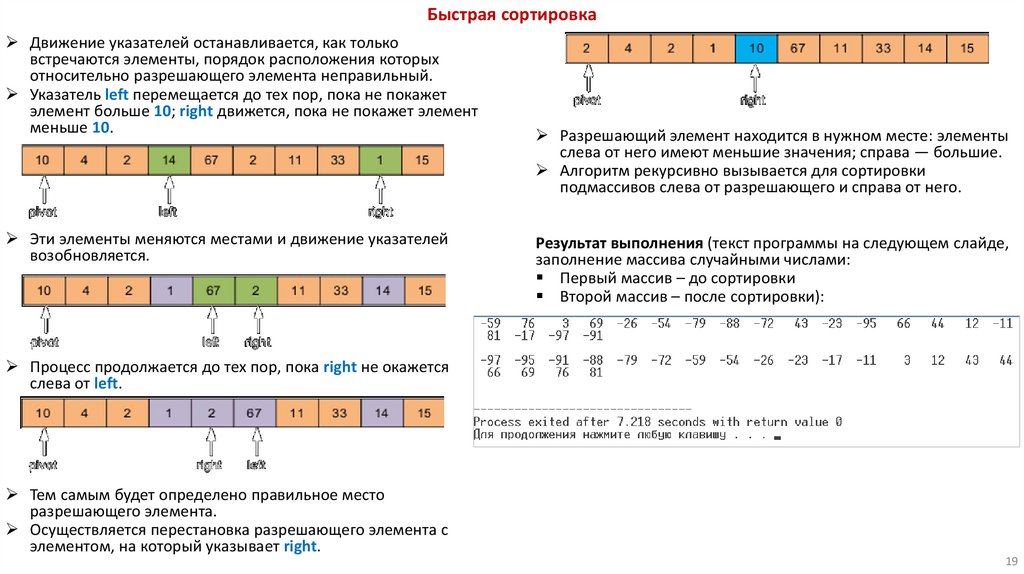
Быстрая сортировка
Движение указателей останавливается, как только
встречаются элементы, порядок расположения которых
относительно разрешающего элемента неправильный.
Указатель left перемещается до тех пор, пока не покажет
элемент больше 10; right движется, пока не покажет элемент
меньше 10.
Эти элементы меняются местами и движение указателей
возобновляется.
Разрешающий элемент находится в нужном месте: элементы
слева от него имеют меньшие значения; справа — большие.
Алгоритм рекурсивно вызывается для сортировки
подмассивов слева от разрешающего и справа от него.
Результат выполнения (текст программы на следующем слайде,
заполнение массива случайными числами:
Первый массив – до сортировки
Второй массив – после сортировки):
Процесс продолжается до тех пор, пока right не окажется
слева от left.
Тем самым будет определено правильное место
разрешающего элемента.
Осуществляется перестановка разрешающего элемента с
элементом, на который указывает right.
19

20.

Быстрая сортировка
#include <stdlib.h>
#define SIZE 20
// Функция быстрой сортировки
void quickSort(int *numbers, int left, int right)
{
int pivot;
// разрешающий элемент
int l_hold = left; //левая граница
int r_hold = right; // правая граница
pivot = numbers[left];
while (left < right) // пока границы не сомкнутся
{
while ((numbers[right] >= pivot) && (left < right))
right--;
// сдвигаем правую границу пока элемент [right]
больше [pivot]
if (left != right) // если границы не сомкнулись
{
numbers[left] = numbers[right]; /* перемещаем элемент [right]
на место разрешающего */
left++; // сдвигаем левую границу вправо
}
while ((numbers[left] <= pivot) && (left < right))
left++; /* сдвигаем левую границу пока элемент [left] меньше
[pivot] */
if (left != right) // если границы не сомкнулись
{
numbers[right] = numbers[left]; /* перемещаем элемент [left]
на место [right] */
right--; // сдвигаем правую границу вправо
}
}
numbers[left] = pivot; // ставим разрешающий элемент на место
pivot = left;
left = l_hold;
right = r_hold;
if (left < pivot) /* Рекурсивно вызываем сортировку для левой и
правой части массива */
quickSort(numbers, left, pivot - 1);
if (right > pivot)
quickSort(numbers, pivot + 1, right);
}
int main()
{
int a[SIZE];
// Заполнение массива случайными числами
for (int i = 0; i<SIZE; i++)
a[i] = rand() % 201 - 100;
// Вывод элементов массива до сортировки
for (int i = 0; i<SIZE; i++)
printf("%4d ", a[i]);
printf("\n");
quickSort(a, 0, SIZE-1); // вызов функции сортировки
// Вывод элементов массива после сортировки
for (int i = 0; i<SIZE; i++)
printf("%4d ", a[i]);
printf("\n");
getchar();
return 0;
}
20

21.

4. Поиск в массиве
Задача – найти в массиве элемент, равный X, или установить,
что его нет.
Решение: для произвольного массива: линейный поиск
(перебор)
недостаток: низкая скорость
Как ускорить? – заранее подготовить массив для поиска
как именно подготовить?
как использовать «подготовленный массив»?
Для нахождения некоторого элемента (ключа) в заданном
неупорядоченном массиве используется алгоритм линейного
(последовательного) поиска. Он работает как с
неотсортированными массивами, так и отсортированными,
но для вторых существуют алгоритмы эффективнее линейного
поиска.
Эту неэффективность компенсируют простая реализация
алгоритма и сама возможность применять его к
неупорядоченным последовательностям. Здесь, а также при
рассмотрении всех других алгоритмов поиска, будем
полагать, что в качестве ключа выступает некоторая величина,
по мере выполнения алгоритма, сравниваемая именно со
значениями элементов массива.
Оценка сложности линейного поиска:
Если суммировать количество шагов, необходимых для
поиска каждого элемента в массиве, получится
1 + 2 + 3 + ... + N = N (N + 1)/2
Разделив сумму на N, чтобы получить среднее
время поиска для всех элементов, получим
(N + 1)/2, а это и есть O(N).
Линейный поиск (Последовательный поиск)
Начинаем просмотр с первого элемента массива,
продвигаясь дальше до тех пор, пока не будет найден нужный
элемент или пока не будут просмотрены все элементы массива.
Алгоритм последовательного поиска
Шаг 1. Полагаем, что значение переменной цикла i=0.
Шаг 2. Если значение элемента массива x[i] равно значению
ключа key, то возвращаем значение, равное номеру искомого
элемента, и алгоритм завершает работу. В противном случае
значение переменной цикла увеличивается на единицу i=i+1.
Шаг 3. Если i<k, где k – число элементов массива x, то
выполняется Шаг 2, в противном случае – работа алгоритма
завершена и возвращается значение равное -1.
При наличии в массиве нескольких элементов со значением
key данный алгоритм находит только первый из них (с
наименьшим индексом).
int LinearSearch(int *x, int k, int key)
{
int i = 0;
for ( i = 0 ; i < k ; i++ )
{
if ( x[i] == key )
break;
}
return i < k ? i : -1; /* “-1” элемент не найден */
}
Это будет худшим случаем O(N).
21

22.

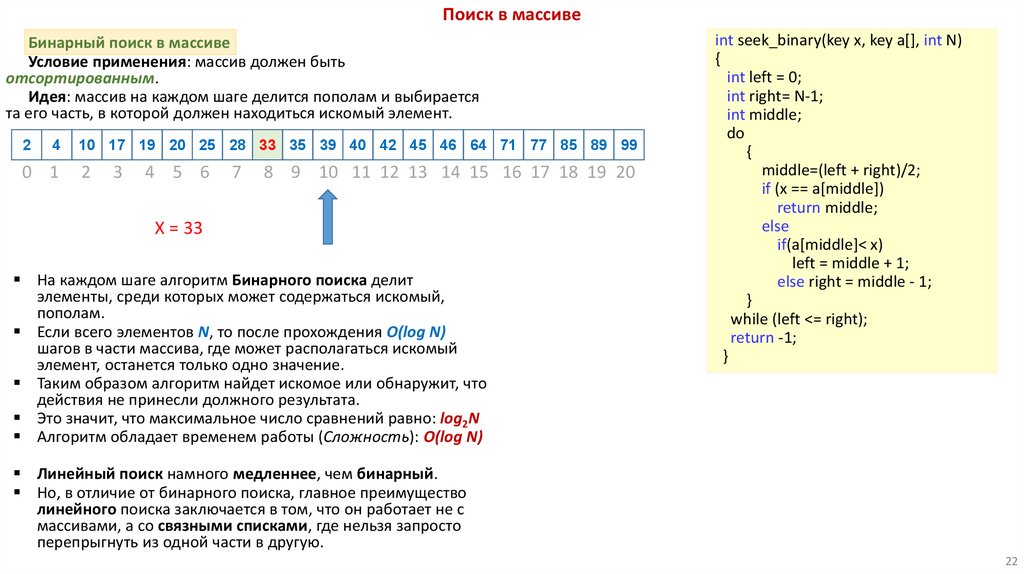
Поиск в массиве
Бинарный поиск в массиве
Условие применения: массив должен быть
отсортированным.
Идея: массив на каждом шаге делится пополам и выбирается
та его часть, в которой должен находиться искомый элемент.
2
4
0 1
10 17 19 20 25 28 33 35 39 40 42 45 46 64 71 77 85 89 99
2
3
4 5 6
7
8 9 10 11 12 13 14 15 16 17 18 19 20
X = 33
На каждом шаге алгоритм Бинарного поиска делит
элементы, среди которых может содержаться искомый,
пополам.
Если всего элементов N, то после прохождения O(log N)
шагов в части массива, где может располагаться искомый
элемент, останется только одно значение.
Таким образом алгоритм найдет искомое или обнаружит, что
действия не принесли должного результата.
Это значит, что максимальное число сравнений равно: log2N
Алгоритм обладает временем работы (Сложность): O(log N)
int seek_binary(key x, key a[], int N)
{
int left = 0;
int right= N-1;
int middle;
do
{
middle=(left + right)/2;
if (x == a[middle])
return middle;
else
if(a[middle]< x)
left = middle + 1;
else right = middle - 1;
}
while (left <= right);
return -1;
}
Линейный поиск намного медленнее, чем бинарный.
Но, в отличие от бинарного поиска, главное преимущество
линейного поиска заключается в том, что он работает не с
массивами, а со связными списками, где нельзя запросто
перепрыгнуть из одной части в другую.
22

23.

5. Связь двумерных массивов с указателями
Имя двумерного массива является указателем-константой на
начало (элемент с индексом 0) массива указателей-констант,
i-й элемент этого массива - указатель-константа на начало
(элемент с индексом 0) i-й строки двумерного массива.
Пример: int b[3][0];
b
b[0]
b[1]
b[2]
b[3]
b[4]
b[0][0]
b[1][0]
b[2][0]
b[3][0]
b[4][0]
b[0][1]
b[1][1]
b[2][1]
b[3][1]
b[4][1]
...
...
...
...
...
b[0][7]
b[1][7]
b[2][7]
b[3][7]
b[4][7]
Обозначения элемента двумерного массива:
b[i][j]
&b[i][j]
*(b[i]+j)
b[i]+j
*(*(b+i)+j);
*(b+i)+j
Для любого из трех обозначений элемента двумерного
массива программа в кодах получается практически
одинаковой по производительности, хотя при использовании
арифметики указателей вместо квадратных скобок программа
будет эффективней.
Хороший стиль программирования предполагает
употребление в пределах одной программы одного из трех
указанных обозначений.
Иногда удобно двумерный (многомерный) массив
рассматривать как одномерный:
#define N 2
#define M 5
...
int a[N][M];
int *p;
...
for (p = &a[0][0]; p <= &a[N-1][M-1]; p++)
*p = 0;
Обработка строки матрицы (обнуление i-ой строки)
// указатель на начало i-ой строки
int *p = &a[i][0];
&a[i][0] => &(*(a[i] + 0)) => &(*a[i]) => a[i]
Т.е. выражение a[i] – это адрес начала i-ой строки.
// обнуление i-ой строки
for (p = a[i]; p < a[i] + M; p++)
*p = 0;
a[i] можно передать любой функции, обрабатывающей
одномерный массив: zero(a[i], M);
23

24.

Связь двумерных массивов с указателями
Обработка столбца матрицы (обнуление j-го столбца)
// указатель на строку (строка – это массив из M элементов)
int (*q)[M];
Скобки важны из-за приоритета операций! Без скобок
получится массив из M указателей.
Выражение q++ смещает указатель на следующую строку
Выражение (*q)[j] возвращает значение в j-ом столбце строки,
на которую указывает q.
for (q = a; q < a + N; q++)
(*q)[j] = 0;
Выводы:
При размещении элементов двумерных массивов они
располагаются в памяти подряд по строкам, т.е. быстрее
всего изменяется последний индекс, а медленнее – первый.
Такой порядок дает возможность обращаться к любому
элементу двумерного массива, используя адрес его
начального элемента и только одно индексное выражение.
int arr[m][n]:
Адрес (arr[i][j])= Адрес(arr[0][0]) + (i*n+j)*k,
Указатели на двумерные массивы в языке Си – это массивы
массивов, т.е. такие массивы, элементами которых являются
массивы.
При объявлении таких массивов в памяти компьютера
создается несколько различных объектов.
Например, при выполнении объявления двумерного массива:
int arr [4][3];
1) В памяти выделяется участок для хранения значения
переменной arr, которая является указателем на массив из
четырех указателей.
2) Для этого массива из четырех указателей тоже выделяется
память. Каждый из этих четырех указателей содержит адрес
одномерного массива из трех элементов типа int.
3) Следовательно, в памяти компьютера выделяется четыре
участка для хранения четырех массивов чисел типа int, каждый
из которых состоит из трех элементов.
Таким образом, объявление arr[4][3] порождает в программе
три разных объекта:
указатель с идентификатором arr,
безымянный массив из четырех указателей:
arr[0], arr[1], arr[2], arr[3]
безымянный массив из двенадцати чисел типа int.
Для доступа к безымянным массивам используются адресные
выражения с указателем arr.
Доступ к элементам одномерного массива указателей
осуществляется с указанием одного индексного выражения в
форме arr[2] или *(arr+2).
Для доступа к элементам двумерного массива чисел типа int
arr[i][j] должны быть использованы следующие выражения:
Например, пусть i=1, j=2, тогда обращение к элементу arr[1][2]:
arr[i][j]
*(*(arr+i)+j)
(*(arr+i))[j]
arr[1][2]=10
*(*(arr+1)+2)=10
(*(arr+1))[2]=10
24

25.

25