ВиС 8 класс 5 урок

1.

Введение
Занимаясь описательной статистикой, мы
говорили о среднем значении, медиане,
наибольшем и наименьшем значениях. Эти
характеристики описывают положение
массива данных на числовой прямой. Для
более полного описания данных нужно
уметь измерять рассеивание данных
относительно своего среднего.
Чаще всего для описания и
измерения
рассеивания
используются дисперсия и
стандартное отклонение.

2.

§ 42
Рассеивание
числовых данных
и отклонения

3.

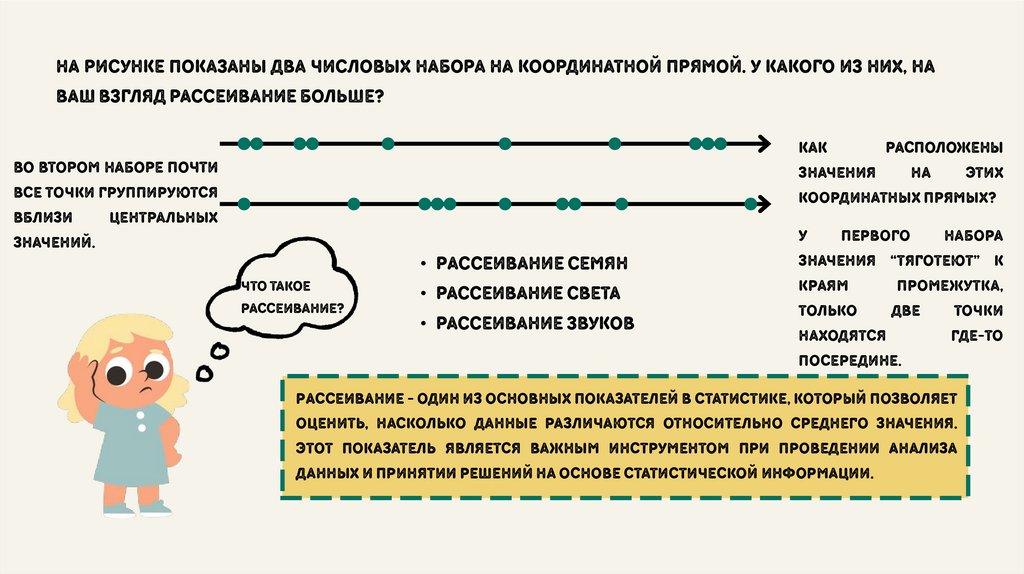
На рисунке показаны два числовых набора на координатной прямой. у какого из них, на
ваш взгляд рассеивание больше?
как
расположены
во втором наборе почти
значения
все точки группируются
координатных прямых?
вблизи
центральных
у
значений.
что такое
рассеивание?
на
первого
этих
набора
• Рассеивание семян
значения “тяготеют” к
• рассеивание света
краям
промежутка,
только
две
• рассеивание звуков
находятся
точки
где-то
посередине.
Рассеивание - один из основных показателей в статистике, который позволяет
оценить, насколько данные различаются относительно среднего значения.
Этот показатель является важным инструментом при проведении анализа
данных и принятии решений на основе статистической информации.

4.

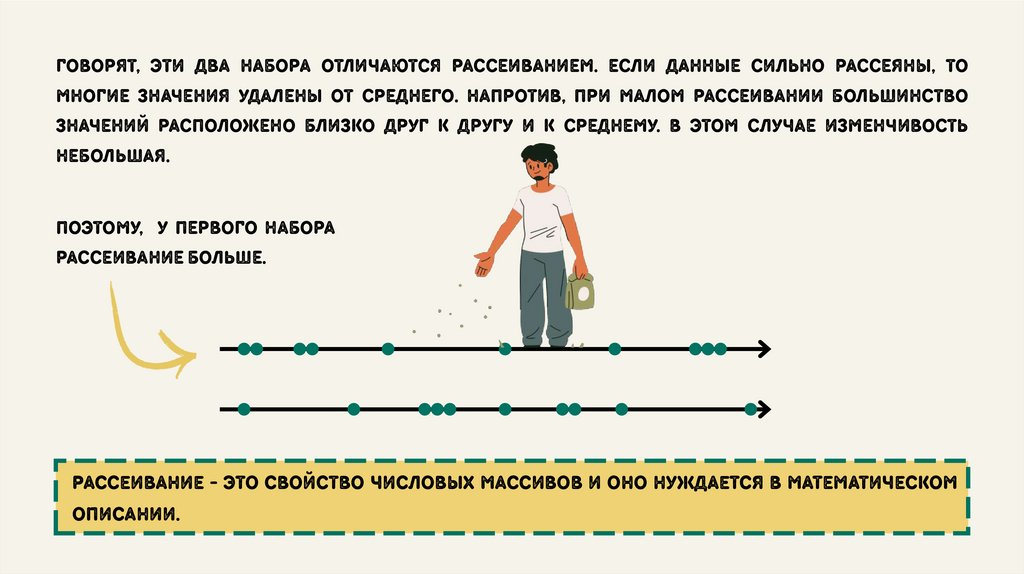
говорят, эти два набора отличаются рассеиванием. если данные сильно рассеяны, то
многие значения удалены от среднего. напротив, при малом рассеивании большинство
значений расположено близко друг к другу и к среднему. в этом случае изменчивость
небольшая.
поэтому, у первого набора
рассеивание больше.
рассеивание - это свойство числовых массивов и оно нуждается в математическом
описании.

5.

Пример 1
Сергей и Иван живут в одном доме и учатся в одной школе. Занятия в школе начинаются в
8 : 30 утра. Каждое утро Сергей выходит из дома в 7 : 55 и идёт в школу пешком. Иван
каждое утро выходит в 8 : 00 и идёт к остановке автобуса. На автобусе до школы всего одна
остановка. В таблице показано время, когда Иван и Сергей входили в школу. Выборка
сделана в разные случайные дни.
Время прихода в школу
Сергей
8 : 15 8 : 14 8 : 14 8 : 15 8 : 16 8 : 15 8 : 25 8 : 15 8 : 14 8 : 16
Иван
8 : 11 8 : 19 8 : 27 8 : 12 8 : 35 8 : 17 8 : 22 8 : 13 8 : 18 8 : 23

6.

Пример 1
Время прихода в школу
Сергей
8 : 15 8 : 14 8 : 14 8 : 15 8 : 16 8 : 15 8 : 25 8 : 15 8 : 14 8 : 16
Иван
8 : 11 8 : 19 8 : 27 8 : 12 8 : 35 8 : 17 8 : 22 8 : 13 8 : 18 8 : 23
ОТВЕТЬТЕ
НА
ВОПРОСЫ
01
Сколько времени в среднем тратит на
дорогу до школы сергей? Иван?
02
Назовите наименьшее и наибольшее время,
затраченное на дорогу Иваном? сергеем?
03
у какого из них, на ваш взгляд рассеивание
больше? Почему так получается?
04
для
измерения
рассеивания
можно
использовать размах. рассчитайте размах
данных у сергея, у ивана.

7.

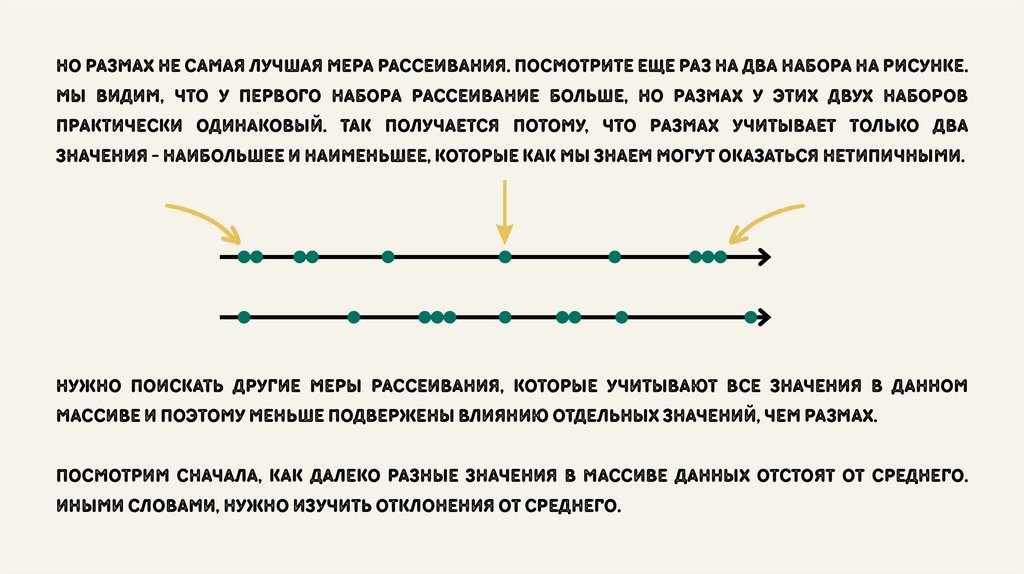
Но размах не самая лучшая мера рассеивания. посмотрите еще раз на два набора на рисунке.
мы видим, что у первого набора рассеивание больше, но размах у этих двух наборов
практически одинаковый. так получается потому, что размах учитывает только два
значения - наибольшее и наименьшее, которые как мы знаем могут оказаться нетипичными.
нужно поискать другие меры рассеивания, которые учитывают все значения в данном
массиве и поэтому меньше подвержены влиянию отдельных значений, чем размах.
посмотрим сначала, как далеко разные значения в массиве данных отстоят от среднего.
иными словами, нужно изучить отклонения от среднего.

8.

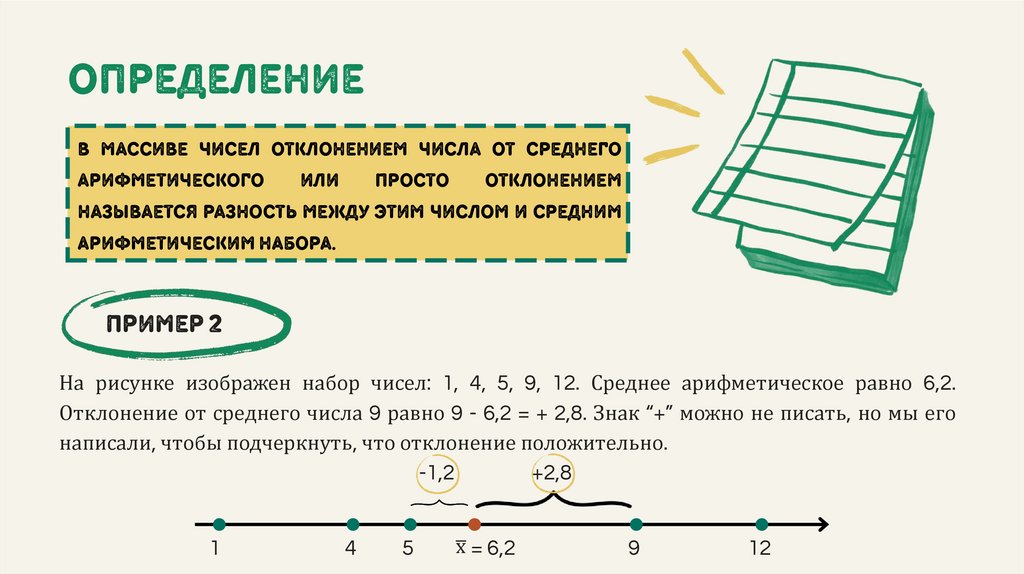
определение
в массиве чисел отклонением числа от среднего
арифметического
или
просто
отклонением
называется разность между этим числом и средним
арифметическим набора.
Пример 2
На рисунке изображен набор чисел: 1, 4, 5, 9, 12. Среднее арифметическое равно 6,2.
Отклонение от среднего числа 9 равно 9 - 6,2 = + 2,8. Знак “+” можно не писать, но мы его
написали, чтобы подчеркнуть, что отклонение положительно.
-1,2
+2,8
4
5
х
1
= 6,2
9
12

9.

Пример 3
Найдите отклонения от среднего арифметического чисел набора 1, 6, 7, 9, 12. Найдите
сумму всех отклонений набора и сделайте вывод.
свойство отклонений
сумма отклонений от среднего арифметического
равна нулю.
.

10.

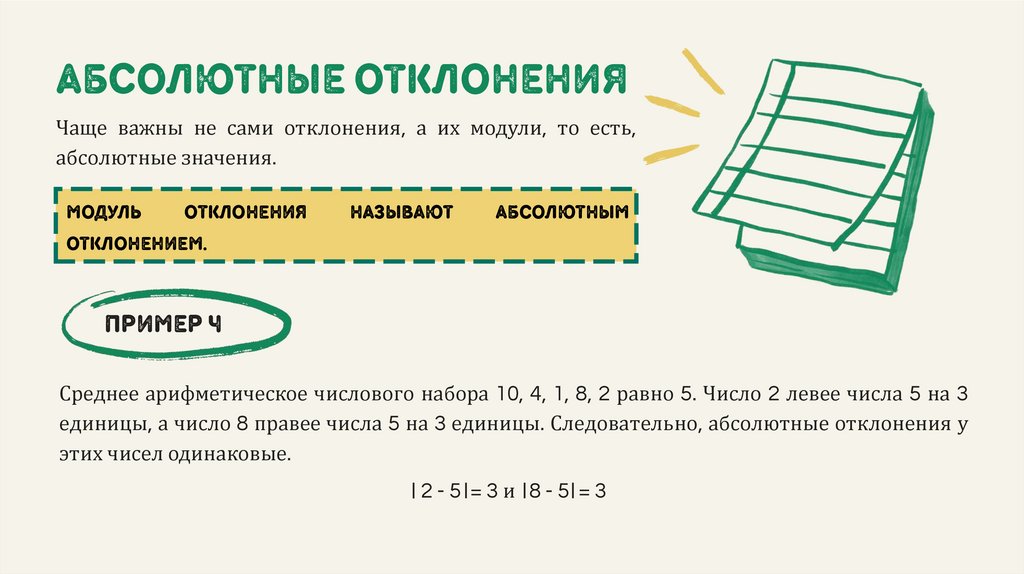
абсолютные отклонения
Чаще важны не сами отклонения, а их модули, то есть,
абсолютные значения.
модуль
отклонения
называют
абсолютным
отклонением.
Пример 4
Среднее арифметическое числового набора 10, 4, 1, 8, 2 равно 5. Число 2 левее числа 5 на 3
единицы, а число 8 правее числа 5 на 3 единицы. Следовательно, абсолютные отклонения у
этих чисел одинаковые.
_
_
_
_
2-5 =3и 8-5 =3

11.

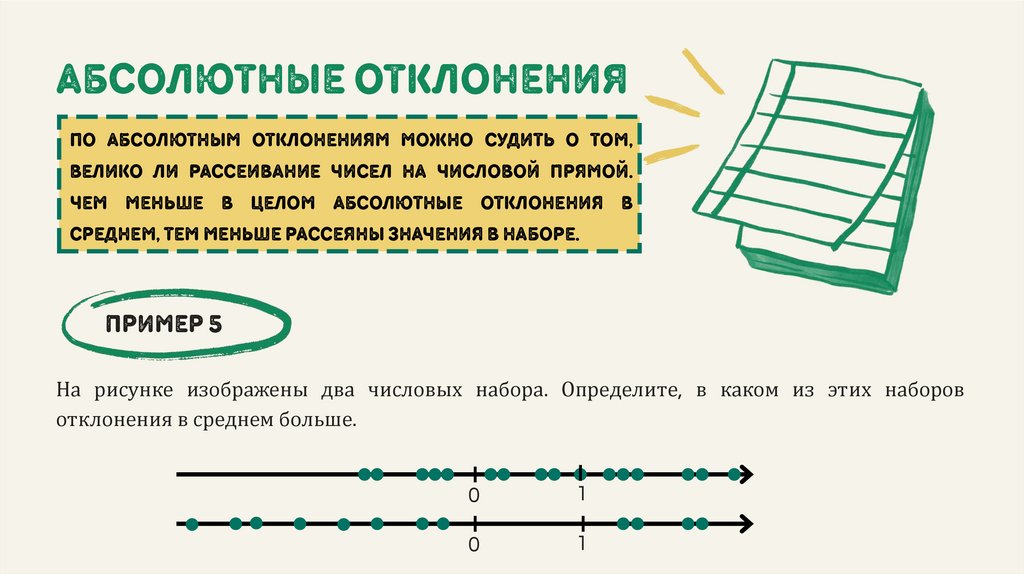
абсолютные отклонения
по абсолютным отклонениям можно судить о том,
велико ли рассеивание чисел на числовой прямой.
чем меньше в целом абсолютные отклонения в
среднем, тем меньше рассеяны значения в наборе.
Пример 5
На рисунке изображены два числовых набора. Определите, в каком из этих наборов
отклонения в среднем больше.
0
1
0
1

12.

Закрепление материала
практическая работа

13.

№1
Даны два набора чисел: 1, 5, 3 и 9, 8, 4. Отметьте числа на числовой
прямой. Не проводя вычислений, определите, у какого из наборов
рассеивание больше.
№2
Найдите отклонения от среднего арифметического набора
чисел: 5, 3, 4, -3, 6.
№3
Дан числовой набор: 2, 7, 8, 5, 3. Найдите в этом наборе два числа,
которые имеют одинаковое абсолютное отклонение от среднего
арифметического.