Дисперсия, стандартное отклонение числовых наборов

1. Дисперсия, стандартное отклонение числовых наборов.

2. Отклонения

Поставим вопрос о том, как числа набора данных расположены по
отношению к своему среднему арифметическому. Зная только размах, мы не
можем судить об этом. Полную информацию даёт набор отклонений.
Определение. В наборе чисел отклонением числа от среднего арифметического называется разность между этим числом и средним
арифметическим набора.
ПРИМЕР 1. На рисунке 29 изображён набор чисел: 1; 4; 5; 9; 12. Среднее
арифметическое равно 6,2. Отклонение числа 9 от среднего равно 9 – 6,2 = +
2,8. Знак « + » можно не писать, но мы написали его, чтобы подчеркнуть, что
отклонение положительно. Число 5 на прямой расположено левее среднего
арифметического. Это значит, что его отклонение отрицательно: 5 – 6,2 = –
1,2.

3. Свойство отклонений

Основное свойство отклонений. Сумма отклонений от среднего арифметического равна нулю. Это свойство удобно использовать для самопроверки при
вычислении отклонений.
ПРИМЕР 2. Отклонения чисел образуют новый числовой набор. Для примера
возьмём набор: 1; 6; 7; 9; 12. Среднее арифметическое этого набора равно 7.
Найдём отклонение каждого числа от среднего:
1 – 7 = – 6,
6 – 7 = – 1,
7 – 7 = 0,
9 – 7 = 2,
12 – 7 = 5.
Если число меньше среднего, то его отклонение отрицательно, если число
больше среднего, то его отклонение положительно. В одном случае – для
числа 7, которое совпало со средним арифметическим, – отклонение равно
нулю.
Если не все числа в наборе совпадают друг с другом, то часть отклонений
положительна, а часть – отрицательна. При этом сумма всех отклонений у
любого набора равна 0. Убедимся в этом на нашем примере:
– 6 – 1 + 0 + 2 + 5 = 0.
Модуль отклонения называют абсолютным отклонением.

4. Дисперсия

5.

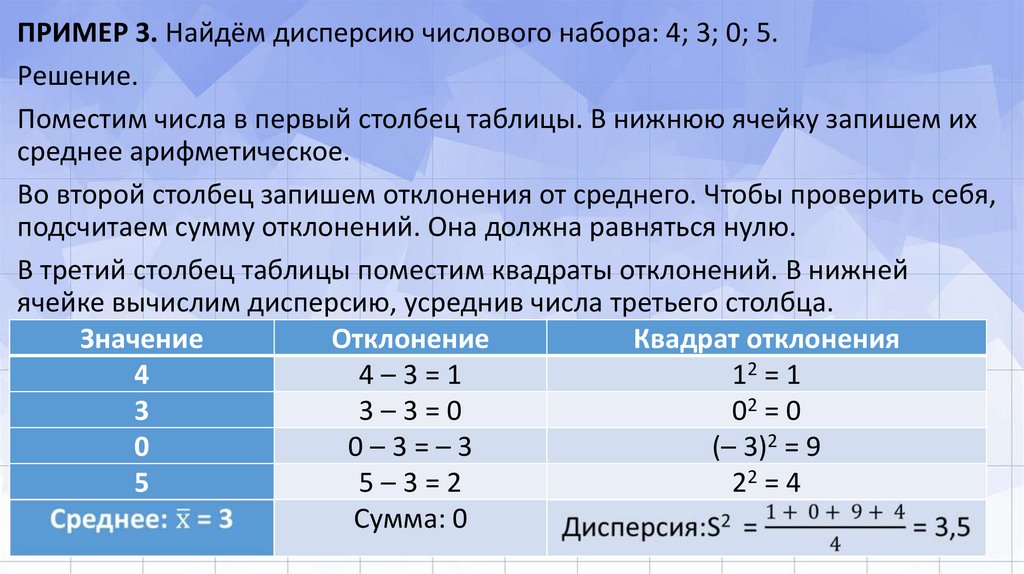
ПРИМЕР 3. Найдём дисперсию числового набора: 4; 3; 0; 5.
Решение.
Поместим числа в первый столбец таблицы. В нижнюю ячейку запишем их
среднее арифметическое.
Во второй столбец запишем отклонения от среднего. Чтобы проверить себя,
подсчитаем сумму отклонений. Она должна равняться нулю.
В третий столбец таблицы поместим квадраты отклонений. В нижней
ячейке вычислим дисперсию, усреднив числа третьего столбца.
Значение
Отклонение
Квадрат отклонения
4
4–3=1
12 = 1
3
3–3=0
02 = 0
0
0–3=–3
(– 3)2 = 9
5
5–3=2
22 = 4
Сумма: 0

6. Стандартное отклонение

7. Пример 4

8. Задание 1

Найдите отклонения от среднего
арифметического чисел набора:
1; – 2; 3; 4; 1; 2;

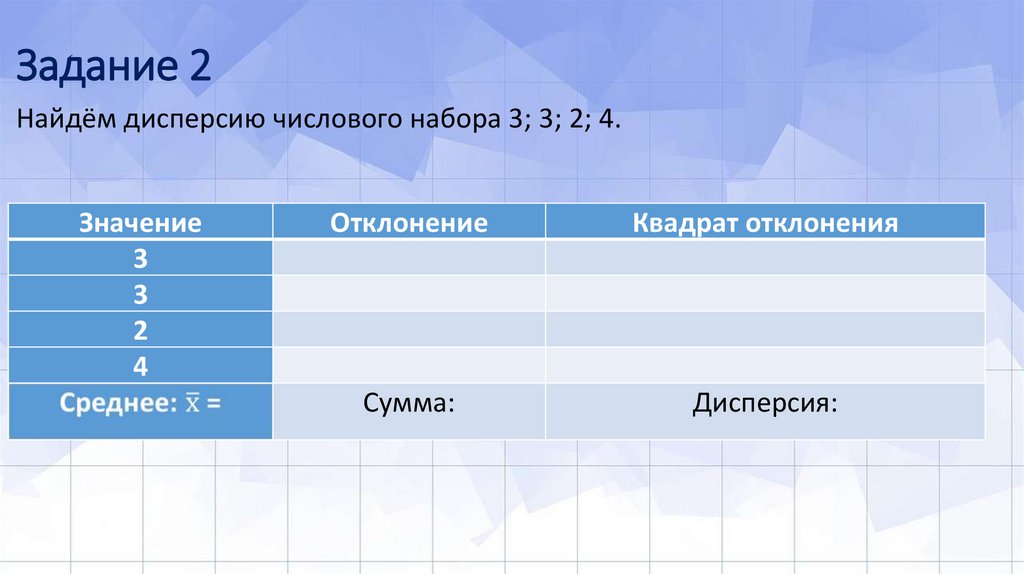
9. Задание 2

Найдём дисперсию числового набора 3; 3; 2; 4.
Значение
3
3
2
4
Отклонение
Квадрат отклонения
Сумма:
Дисперсия:

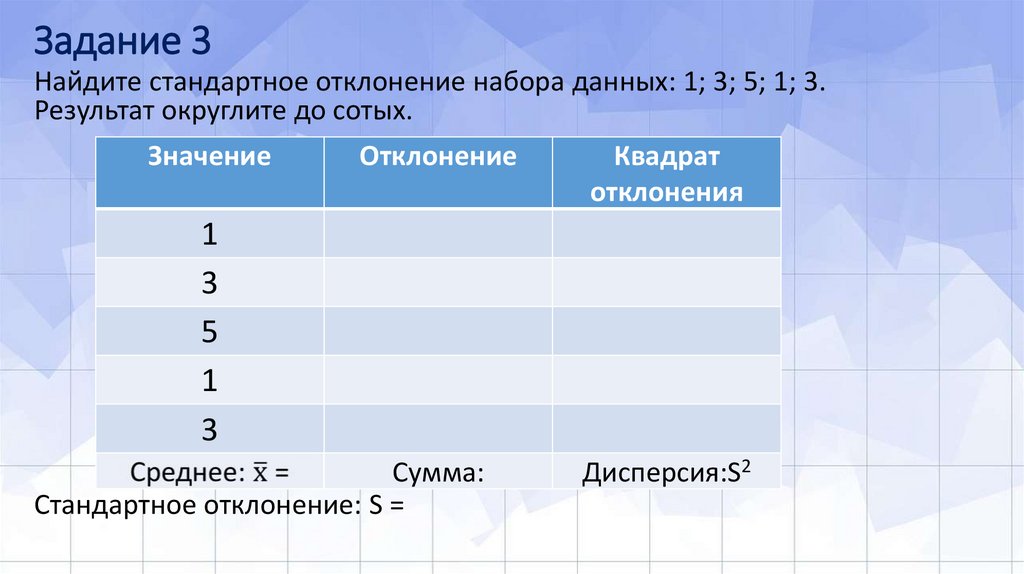
10. Задание 3

Найдите стандартное отклонение набора данных: 1; 3; 5; 1; 3.
Результат округлите до сотых.
Значение
Отклонение
Квадрат
отклонения
1
3
5
1
3
Сумма:
Стандартное отклонение: S =
Дисперсия:S2

11. Домашнее задание:

Прочитать Глава 9, п. 42, 43, 44
Выполнить задания
№ 305 (б) Найдите отклонения от среднего арифметического чисел
набора:
б) – 2,5; 3,1; 5,3; – 1,3; 4,8.
№312 (а, в, д)
№318