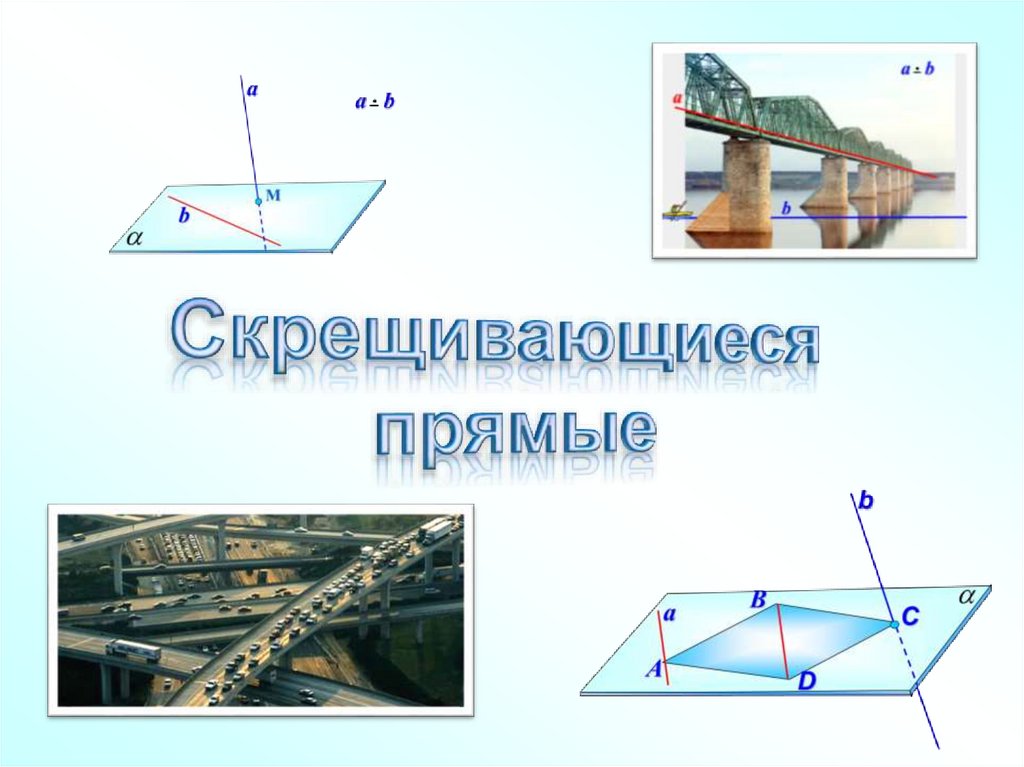
Skreschivayuschiesya_pryamye

1.

2.

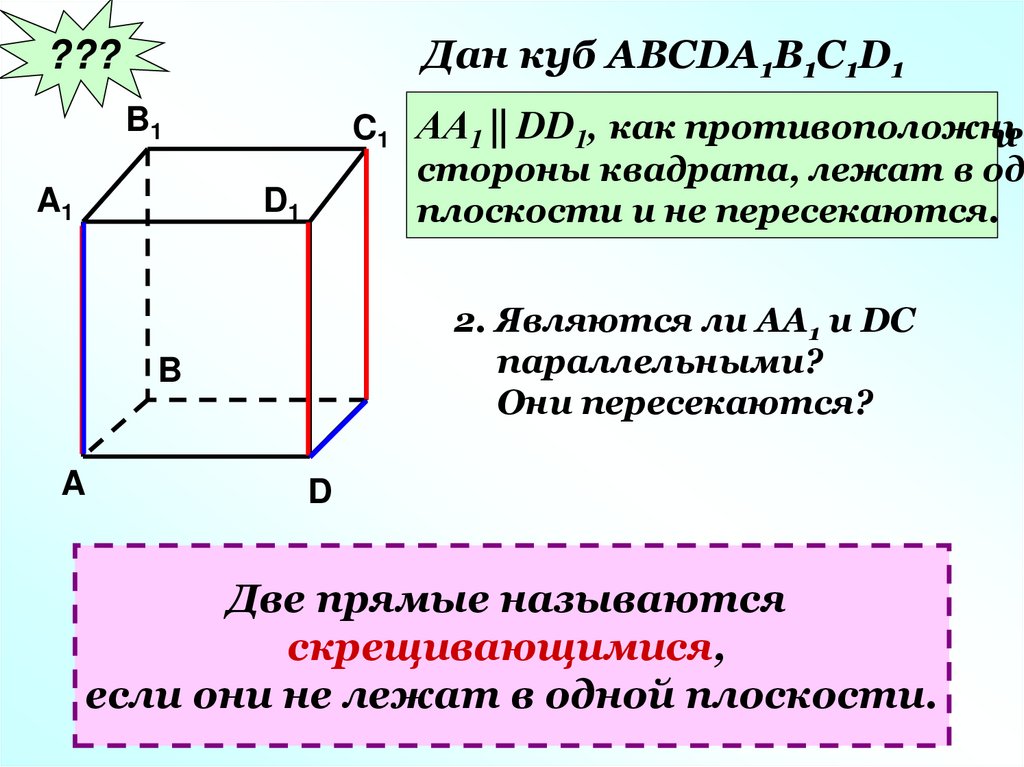
Дан куб АВСDA1B1C1D1
???
АА
C1 1.
Являются
липротивоположны
параллельными
1 || DD1, как
стороны
лежат
в одн
прямые квадрата,
АА1 и DD1; АА
1 и СС1 ?
плоскости
Почему? и не пересекаются.
B1
A1
D1
2. Являются ли АА1 и DC
параллельными?
Они пересекаются?
B
A
D
Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.

3.

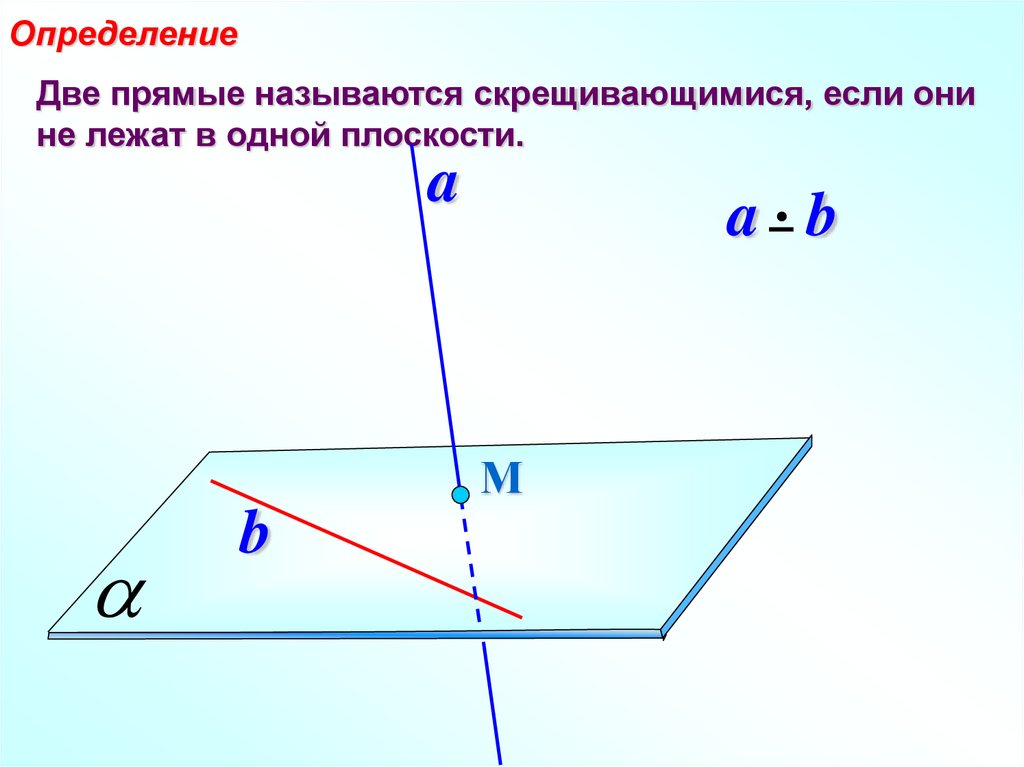
Определение
Две прямые называются скрещивающимися, если они
не лежат в одной плоскости.
a
a b
М
b

4.

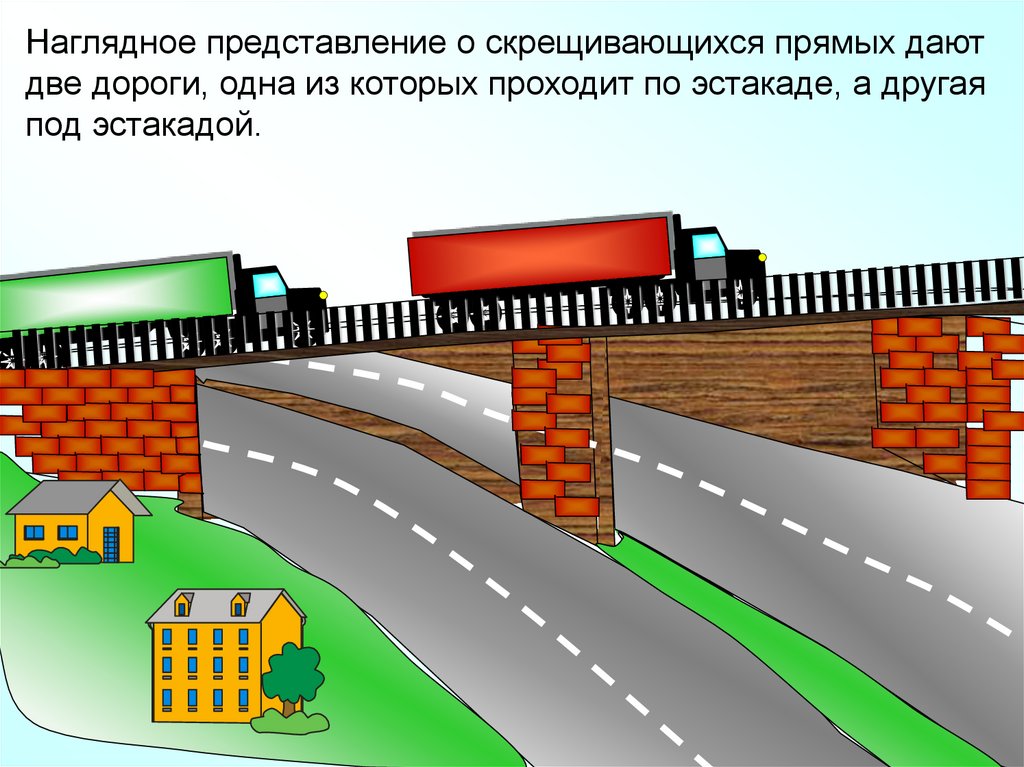
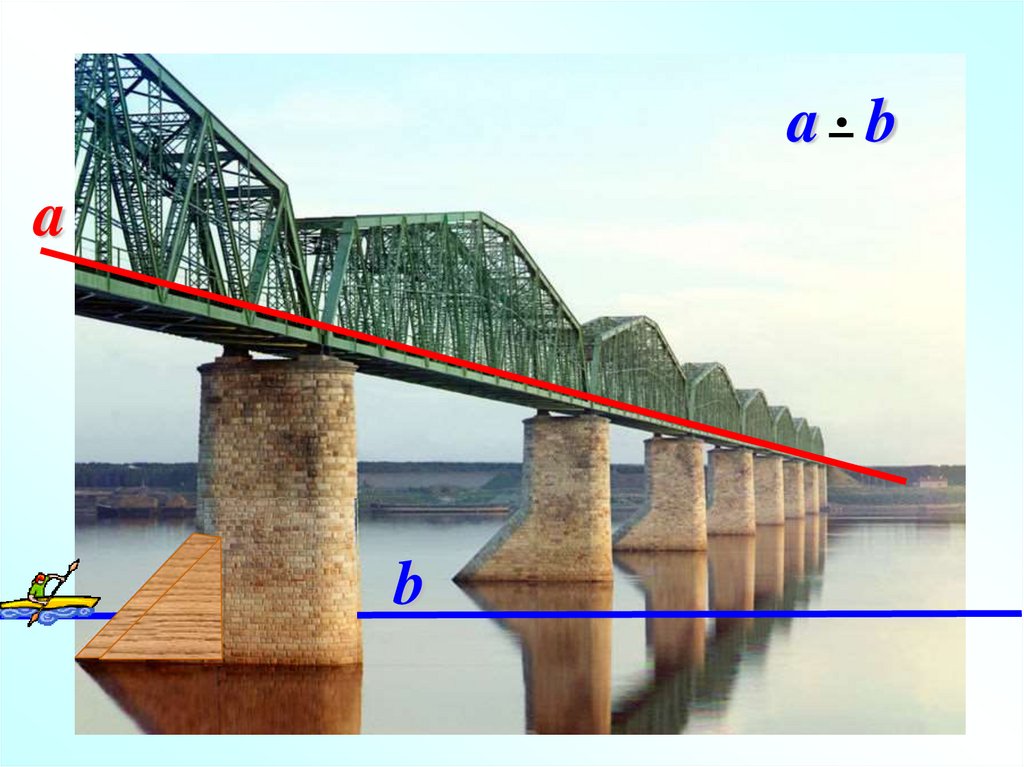
Наглядное представление о скрещивающихся прямых дают
две дороги, одна из которых проходит по эстакаде, а другая
под эстакадой.

5.

a b
a
b

6.

Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

7.

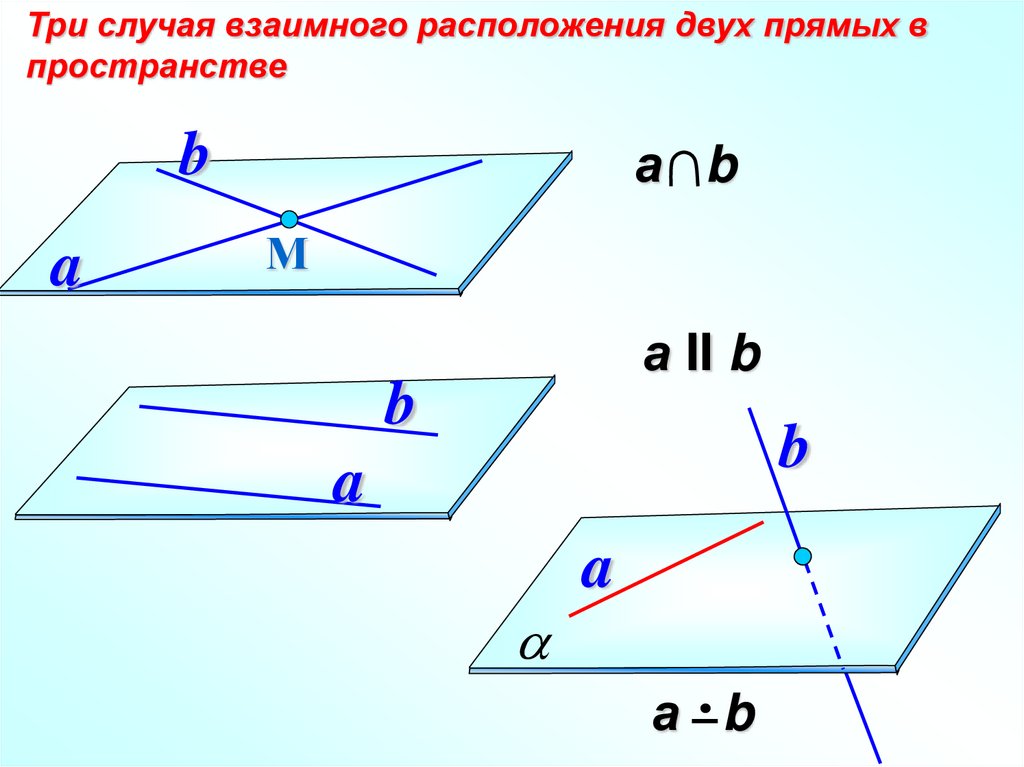
Три случая взаимного расположения двух прямых в
пространстве
b
a
а b
М
а II b
b
b
a
a
а b

8.

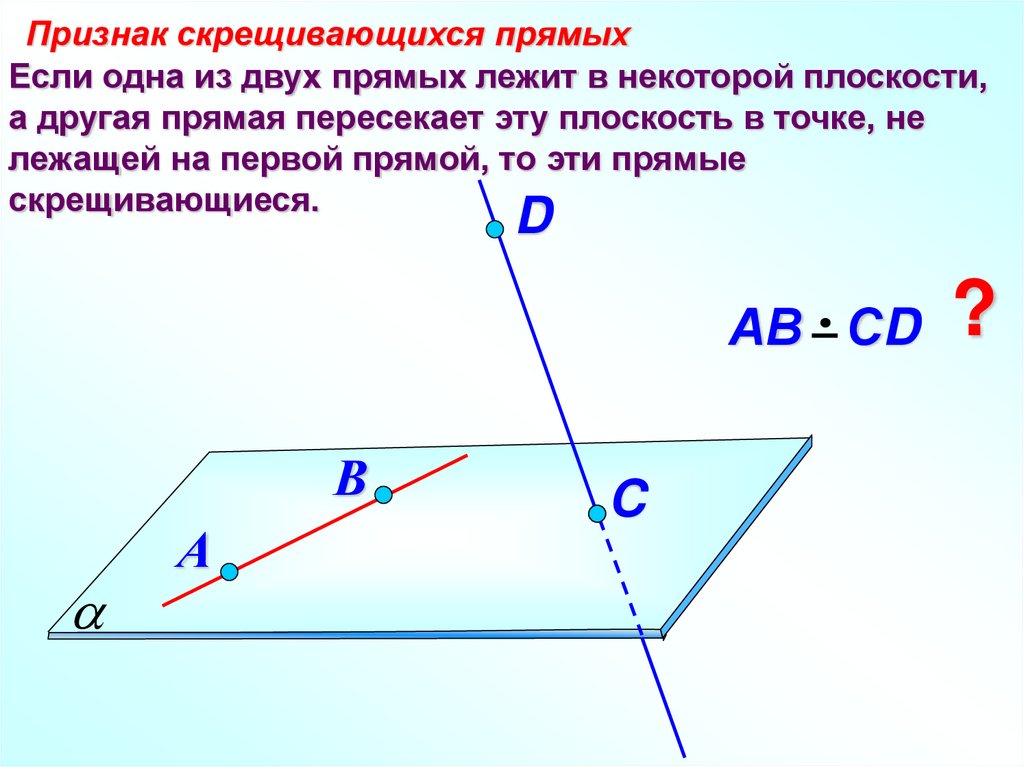
Признак скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости,
а другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые
скрещивающиеся.
D
АВ СD ?
В
А
C

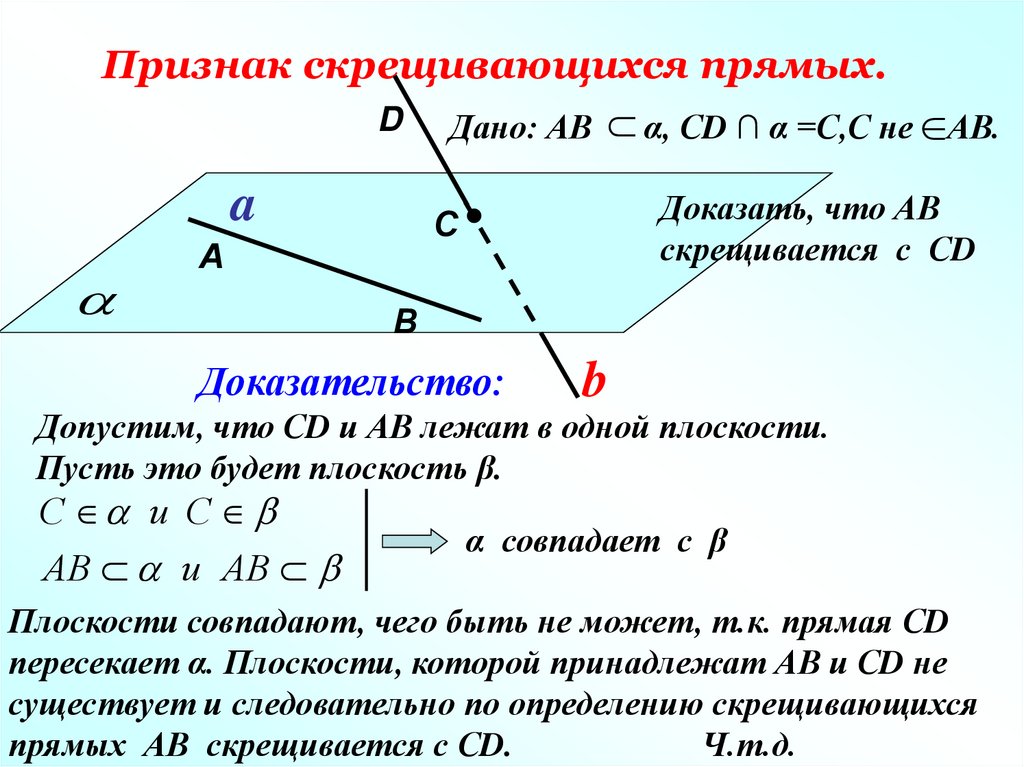
9. Признак скрещивающихся прямых.

D
a
Дано: АВ α, СD ∩ α =С,С не АВ.
Доказать, что АВ
скрещивается с СD
С
А
В
Доказательство:
b
Допустим, что СD и АВ лежат в одной плоскости.
Пусть это будет плоскость β.
С и С
АВ и АВ
α совпадает с β
Плоскости совпадают, чего быть не может, т.к. прямая СD
пересекает α. Плоскости, которой принадлежат АВ и СD не
существует и следовательно по определению скрещивающихся
прямых АВ скрещивается с СD.
Ч.т.д.

10.

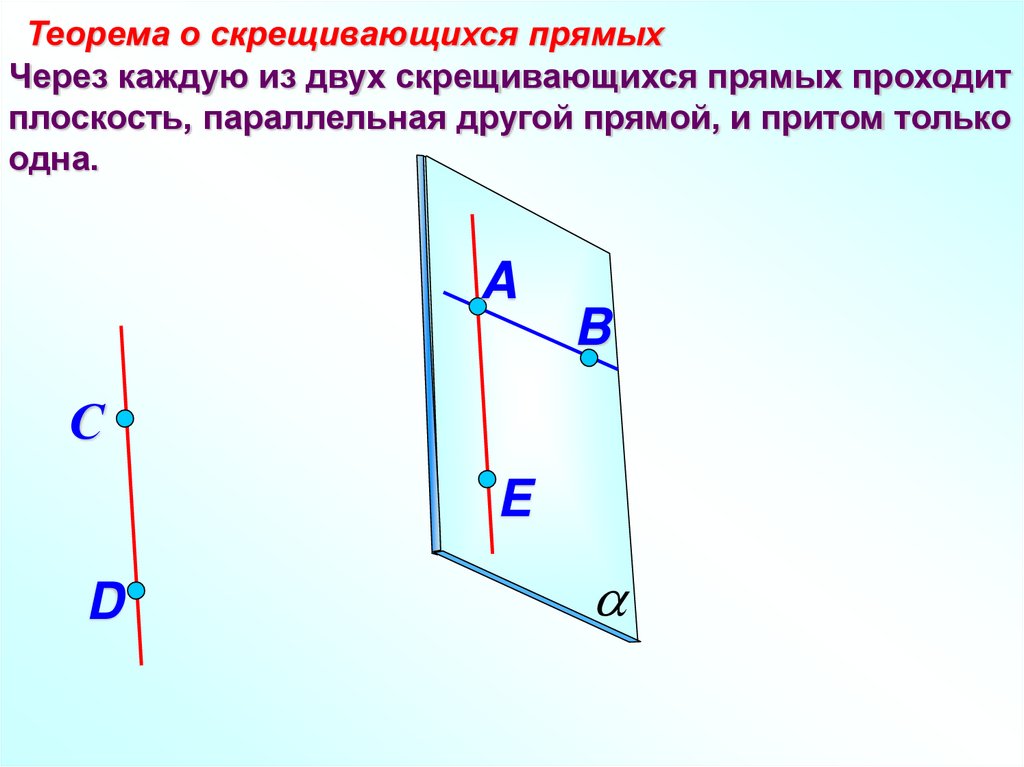
Теорема о скрещивающихся прямых
Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только
одна.
A
B
С
E
D

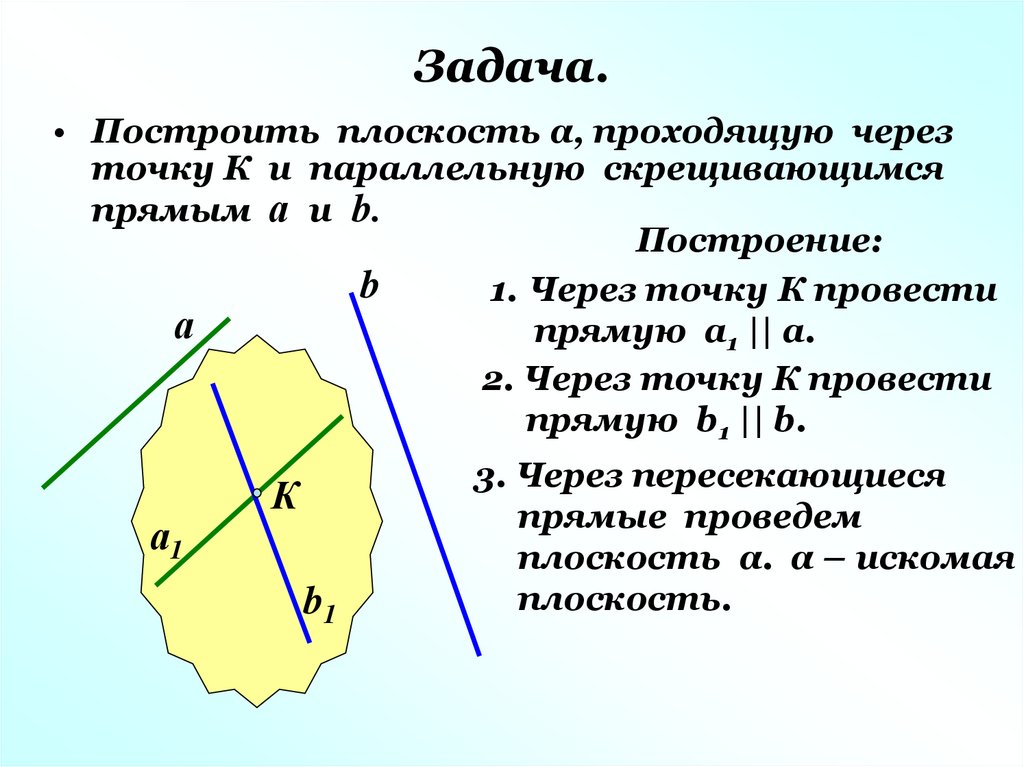
11. Задача.

• Построить плоскость α, проходящую через
точку К и параллельную скрещивающимся
прямым а и b.
Построение:
b
1. Через точку К провести
а
прямую а1 || а.
2. Через точку К провести
прямую b1 || b.
а1
К
b1
3. Через пересекающиеся
прямые проведем
плоскость α. α – искомая
плоскость.

12.

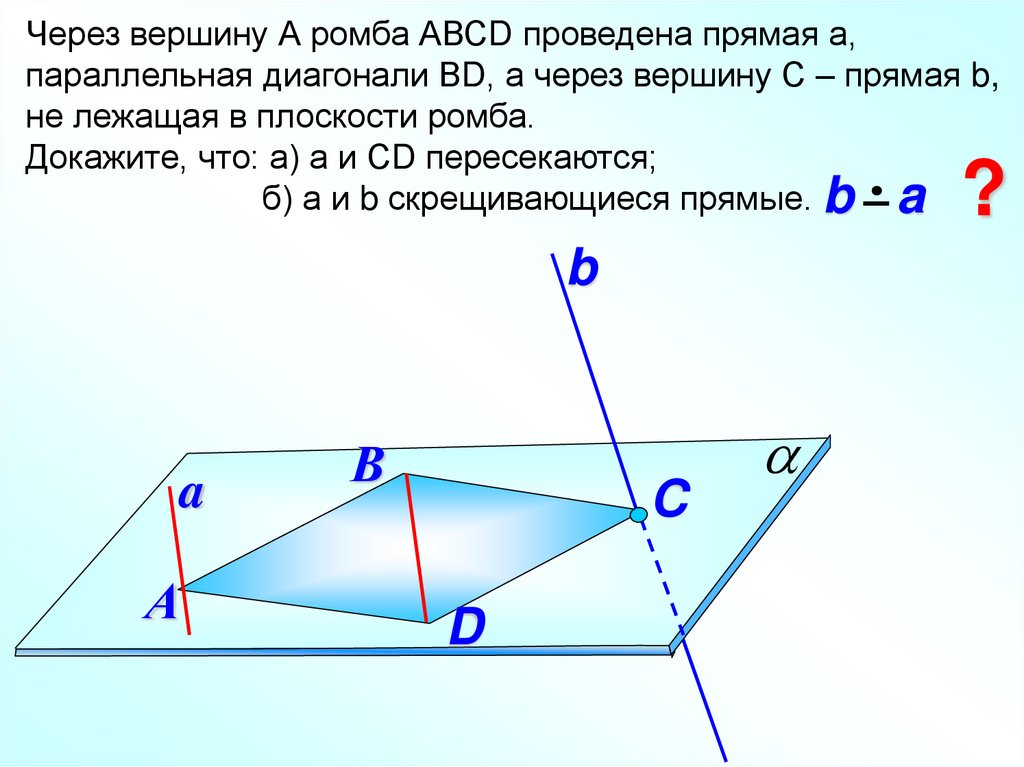
Через вершину А ромба АВСD проведена прямая а,
параллельная диагонали ВD, а через вершину С – прямая b,
не лежащая в плоскости ромба.
Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые. b a
?
b
a
А
В
C
D

13.

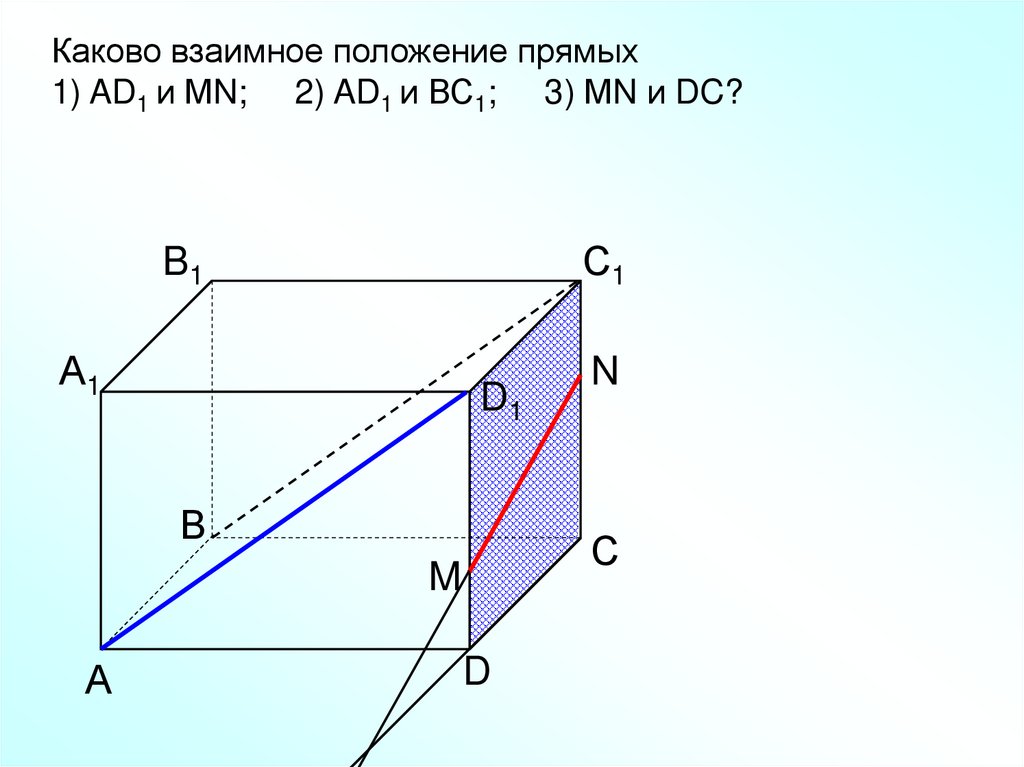
Каково взаимное положение прямых
1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC?
С1
B1
А1
D1
В
С
M
А
N
D

14.

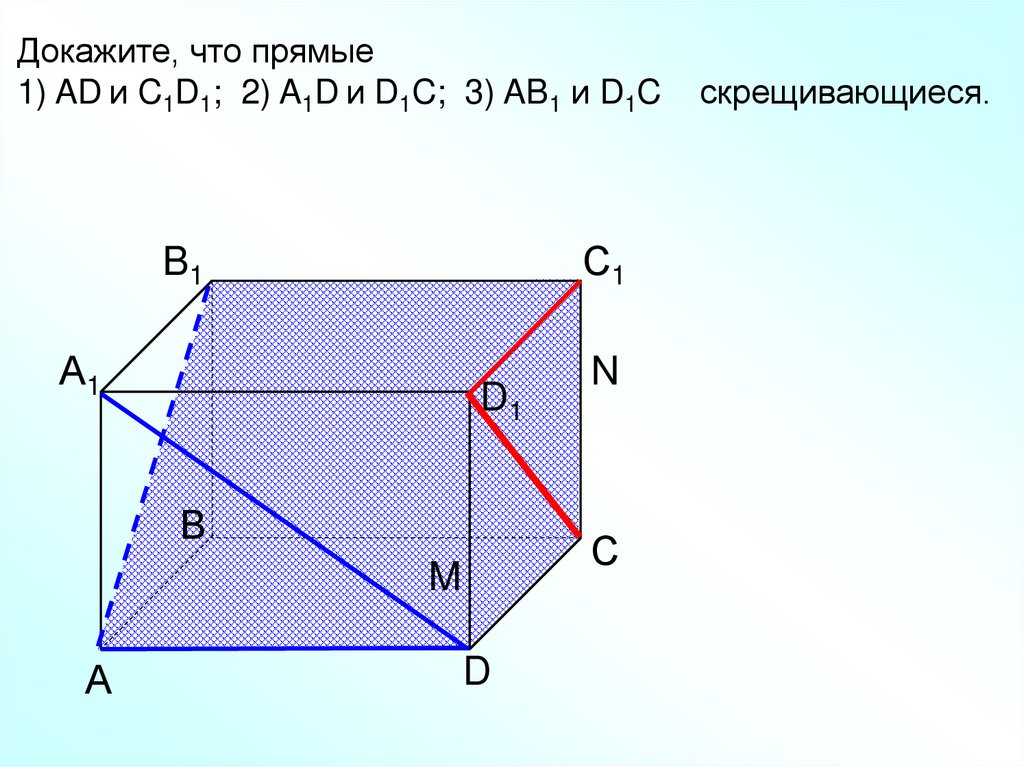
Докажите, что прямые
1) AD и C1D1; 2) A1D и D1C; 3) AB1 и D1C
С1
B1
А1
D1
В
С
M
А
N
D
скрещивающиеся.

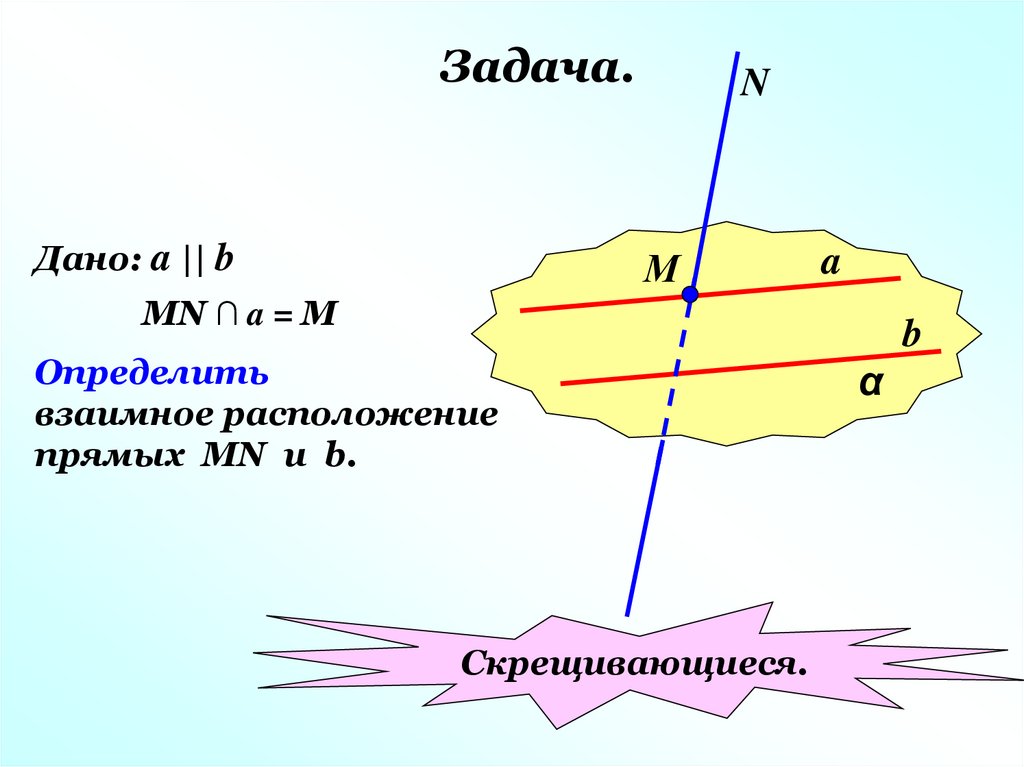
15. Задача.

Дано: a || b
N
М
a
MN ∩ a = M
Определить
взаимное расположение
прямых MN u b.
Скрещивающиеся.
b
α

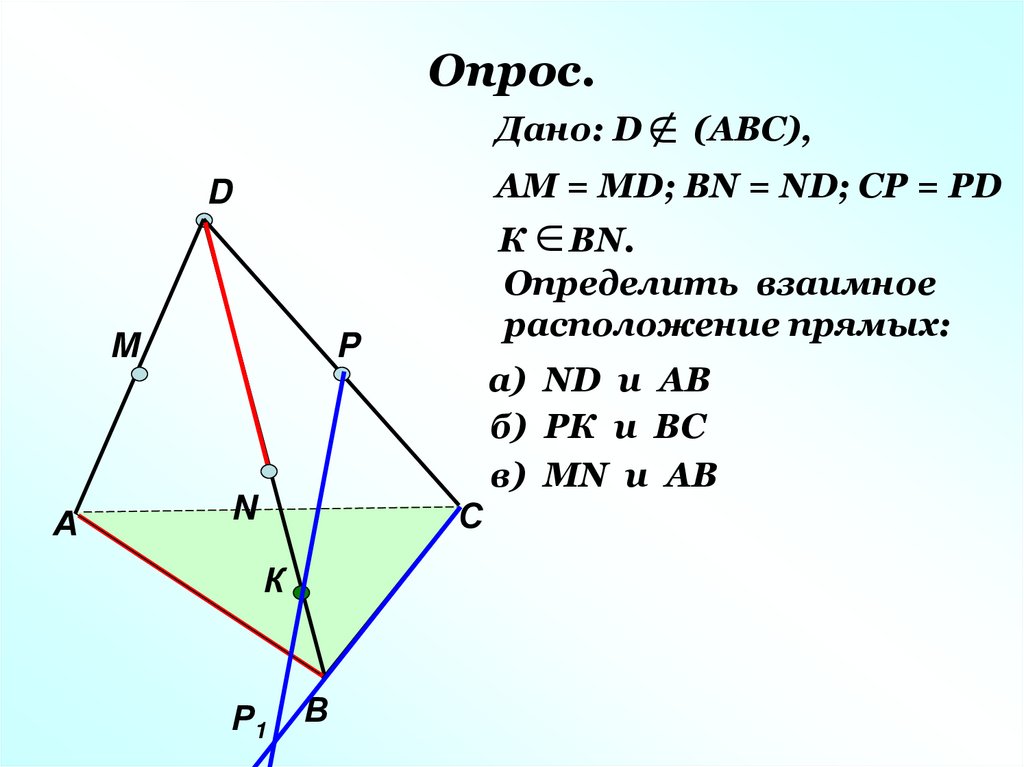
16. Опрос.

Дано: D
АМ = МD; ВN = ND; CP = PD
D
M
А
(АВС),
К ВN.
Определить взаимное
расположение прямых:
P
N
а) ND и AB
б) РК и ВС
в) МN и AB
С
К
Р1
В

17.

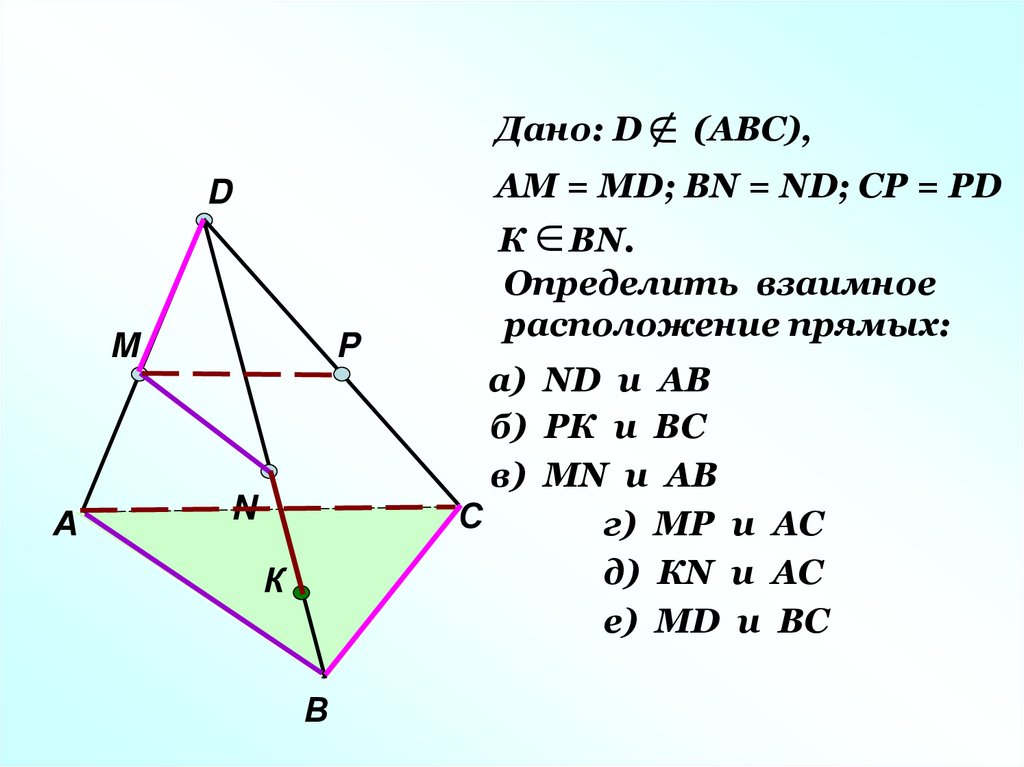
Дано: D
АМ = МD; ВN = ND; CP = PD
D
M
А
(АВС),
P
N
К
В
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
С
г) МР и AС
д) КN и AС
е) МD и BС

18.

1. Верно ли утверждение: если две прямые не имеют общих точек, то они
параллельны?
2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а)
пересекаться; б) быть скрещивающимися?
3. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с ? Ответ
обоснуйте.
4. Прямая а скрещивается с прямой в, а прямая в скрещивается с прямой с .
Следует ли из этого, что прямые а и с скрещивающиеся?
5. Каково должно быть взаимное расположение трех прямых, чтобы можно было
провести плоскость, содержащую все прямые?
6. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся
прямых?
7. Даны две пересекающиеся плоскости. В одной из них лежит прямая а, в другой
плоскости - прямая в. Лежат ли прямые а и в в одной плоскости, если известно,
что они пересекают линию пересечения плоскостей : а) в одной точке; б) в разных
точках.
8. Даны две параллельные плоскости . В одной плоскости лежит прямая а, в
другой плоскости - прямая в. Каковы взаимные случаи расположения прямых а и
в?
9. В плоскости двух параллельных прямых а и в дана точка С, не лежащая на этих
прямых. Прямая с проходит через точку С. Как может быть расположена
прямая с относительно прямых а и в?