Рекомендации по выполнению контрольной работы

1. ВНИМАНИЕ !

*
На слайдах даны примеры вычислений и
оформления заданий контрольной работы.
Формулировка самих заданий приведена в
приложении 1 учебно-методического пособия к
практическим занятиям (по вариантам).
Формулировка правил, по которым должны
решаться задания приведены в практическом занятии
№2 того же пособия.
Цветом выделены «подсказки».

2. а) 567 - 3 б) 0,567 – 3 в) 56700 – 5 г) 5067 – 4 д) 0,00567 х 102 - 3

Задание №1
*

3. Задание №2

*
* Например: необходимо оставить три значащих цифры (для
проверки: левая и правая части равенства должны быть
равны!)
* а) 24537
* 1) 245 – оставляем три значащих цифры
* 2) 245 х 102 - приравниваем левую и правую части равенства, вводя множитель 10
* Записываем только ответ:
* 24537 = 245 х 102
* б) 0,6321 х 105
* 1) 632
* 2) 632 х 10-3
* 3) 632 х 10-3 х 105
* 0,6321 х 105 = 632 х 10-3 х 105 = 632 х 102
*
ИЛИ
* 0,6321 х 105 = 0,632 х 105
к

4. Задание №3

*
* 56 ± 1,365 = 56 ± 1
* 476,8976 ± 3,4 = 476,9 ± 3,4
* 0,0000086 ± 0,0000001 = (86 ± 1)х 10-7
* Внимание! Должно быть одинаковое количество знаков после
запятой и в истинном значении числа, и в абсолютной погрешности.

5. Задание №4

*
* При сложении и вычитании «ищем» число с
наименьшим количеством знаков после запятой. В
ответе должно быть такое же количество знаков
после запятой.
* 34 + 5,734 – 0,67 х 10-7 = 39,734 = 40
* (ответ округляем до целых)
* При умножении и делении «ищем» число с
наименьшим количеством значащих цифр. В ответе
должно быть такое же количество значащих цифр.
* 0,5789 х 24 = 13,8936 = 14
* (ответ округляем до двух значащих цифр)
* В сложных примерах округления выполняем
последовательно и записываем подробно.
* 6,5489 – 3,2 = 3,3 = 0,66 = 0,7
* 3,3 + 2
5
* (в ответе оставляем одну значащую цифру)

6. Задание № 5

*
* Абсолютная погрешность: Δ = Хист - Хi
* Относительная погрешность: δ = (Δ / Хист )х100%
* Из задания №3 (в расчет брать ответы!):
* 56 ± 1
* δ = (1/56)х100% = 1,8 %

7. Задание № 6

*
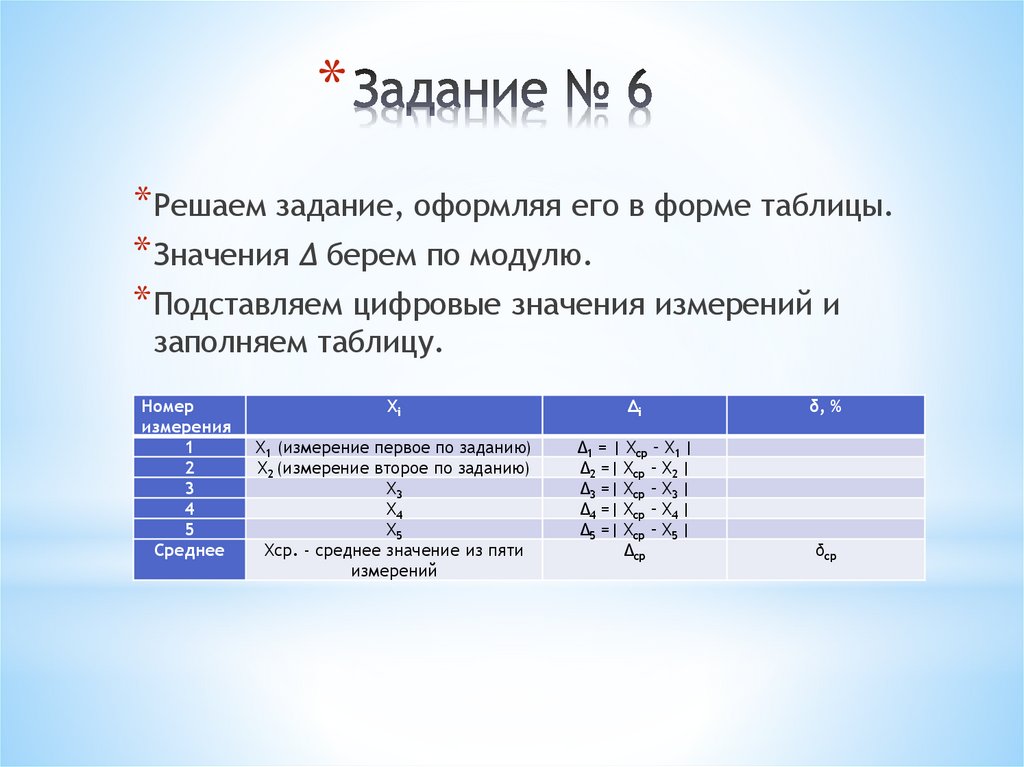
* Решаем задание, оформляя его в форме таблицы.
* Значения Δ берем по модулю.
* Подставляем цифровые значения измерений и
заполняем таблицу.
Номер
измерения
1
2
3
4
5
Среднее
Хi
Δi
δ, %
Х1 (измерение первое по заданию)
Х2 (измерение второе по заданию)
Х3
Х4
Х5
Хср. - среднее значение из пяти
измерений
Δ1 = | Хср – Х1 |
Δ2 =| Хср – Х2 |
Δ3 =| Хср – Х3 |
Δ4 =| Хср – Х4 |
Δ5 =| Хср – Х5 |
Δср
δср

8. Задание №7 и №8 (для вычислений применяются одни и те же правила для чисел с погрешностями)

*
* СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЧИСЕЛ С ПОГРЕШНОСТЯМИ
* (9 ± 2) + (3 ± 1) = (9 + 3) ± (2+1) = (12 ± 3)
*
сумма истинных
сумма абсолютных
*
*
значений чисел
погрешностей
каждого из чисел
* (9 ± 2) - (3 ± 1) = (6 ± 3)
* ПОГРЕШНОСТИ ВСЕГДА СУММИРУЮТСЯ, НЕСМОТРЯ НА
ЗНАК!!!

9. ДЕЛЕНИЕ И УМНОЖЕНИЕ ЧИСЕЛ С ПОГРЕШНОСТЯМИ

*
* (9 ± 2) : (3 ± 1) = (9 : 3) ± (2/9 + 1/3) =
*
*
*
Х
Δ
Х
Δ
сумма относительных
погрешностей каждого
из чисел
* = 3 ± (0,22 + 0,33) = 3 ± 0,6 = 3,0 ± 0,6 (в ответе
должно быть одинаковое количество знаков после запятой!!!)
* ПРИМЕРЫ
* (4 ± 1)∙(6 ± 2) = (4 ∙ 6) ± (1/4 + 2/6 + 1/3) =
* (3 ± 1)
3
* = 8 ± (0,25+0,33+0,33) = 8,0 ± 0,9
* (10 ± 2) - (5 ± 1) = (5 ± 3) = (5/8) ± (3/5+4/8) =
* (8 ± 4)
(8 ± 4)
* = 0,62 ± (0,6+0,5) = 0,6 ± 1,1