Теория измерений. Классификация погрешностей измерений

1.

Теория измерений

2.

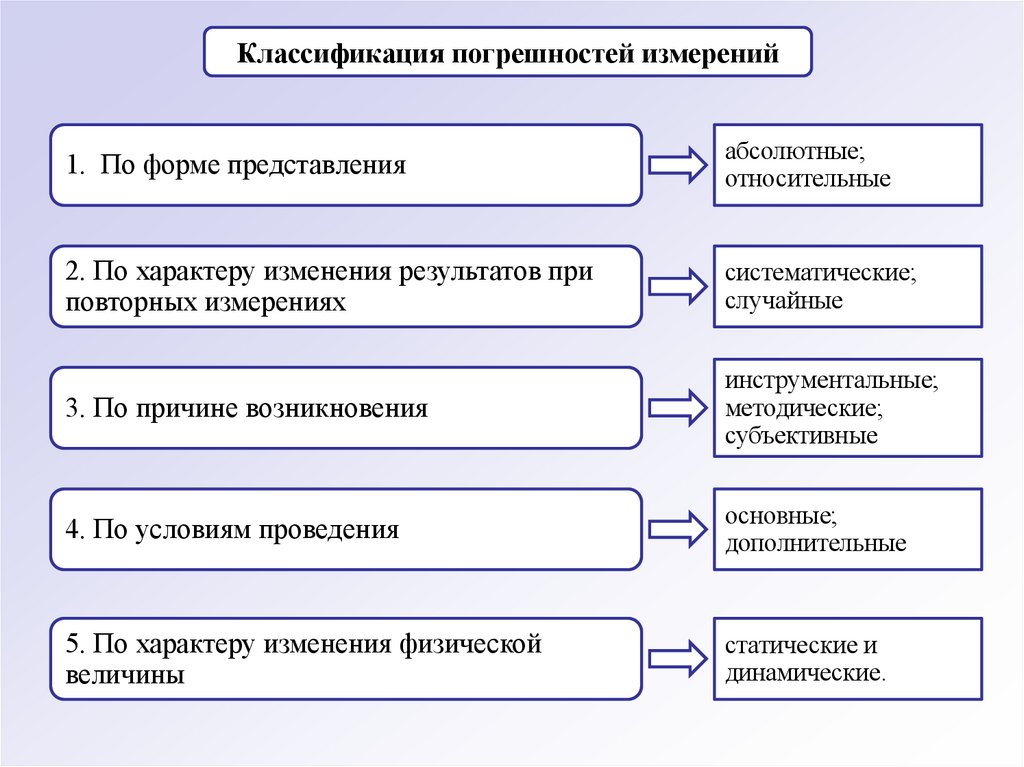
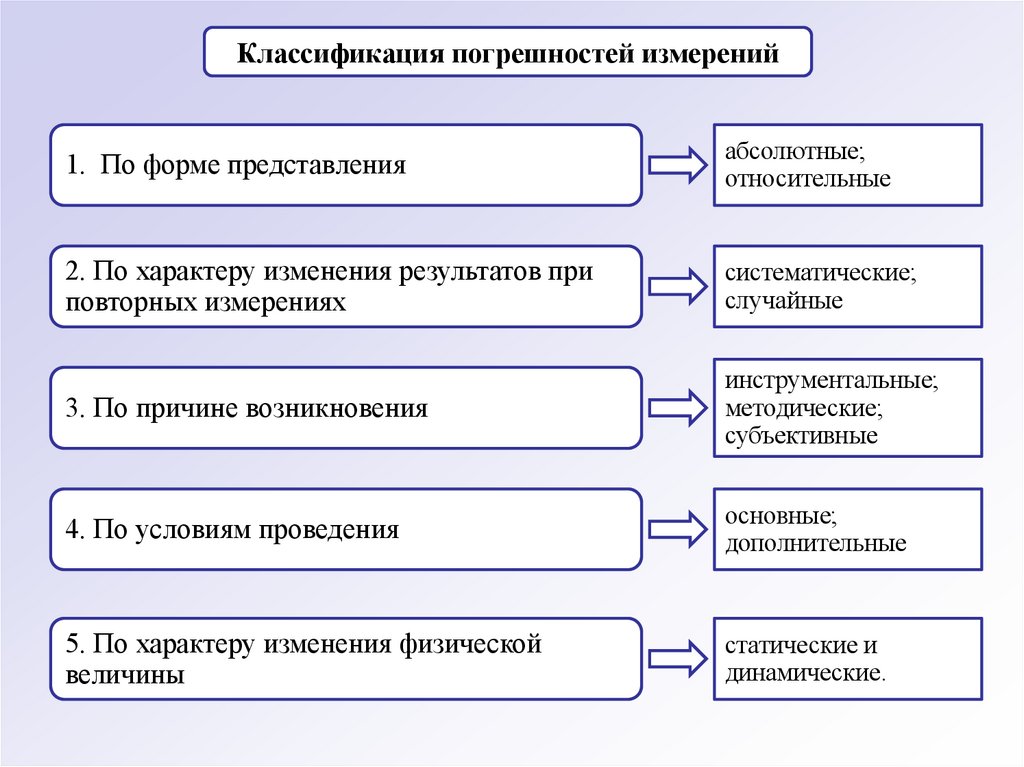
Классификация погрешностей измерений
1. По форме представления
абсолютные;
относительные
2. По характеру изменения результатов при
повторных измерениях
систематические;
случайные
3. По причине возникновения
инструментальные;
методические;
субъективные
4. По условиям проведения
основные;
дополнительные
5. По характеру изменения физической
величины
статические и
динамические.

3.

Абсолютная погрешность измерений
X изм Х изм Х д
Относительная погрешность измерений
Х
изм
Хд
Х
изм
100%
Хд
Хизм – измеренное значение величины, Хд – действительное значение величины.

4.

Классификация погрешностей измерений
1. По форме представления
абсолютные;
относительные
2. По характеру изменения результатов при
повторных измерениях
систематические;
случайные
3. По причине возникновения
инструментальные;
методические;
субъективные
4. По условиям проведения
основные;
дополнительные
5. По характеру изменения физической
величины
статические и
динамические.

5.

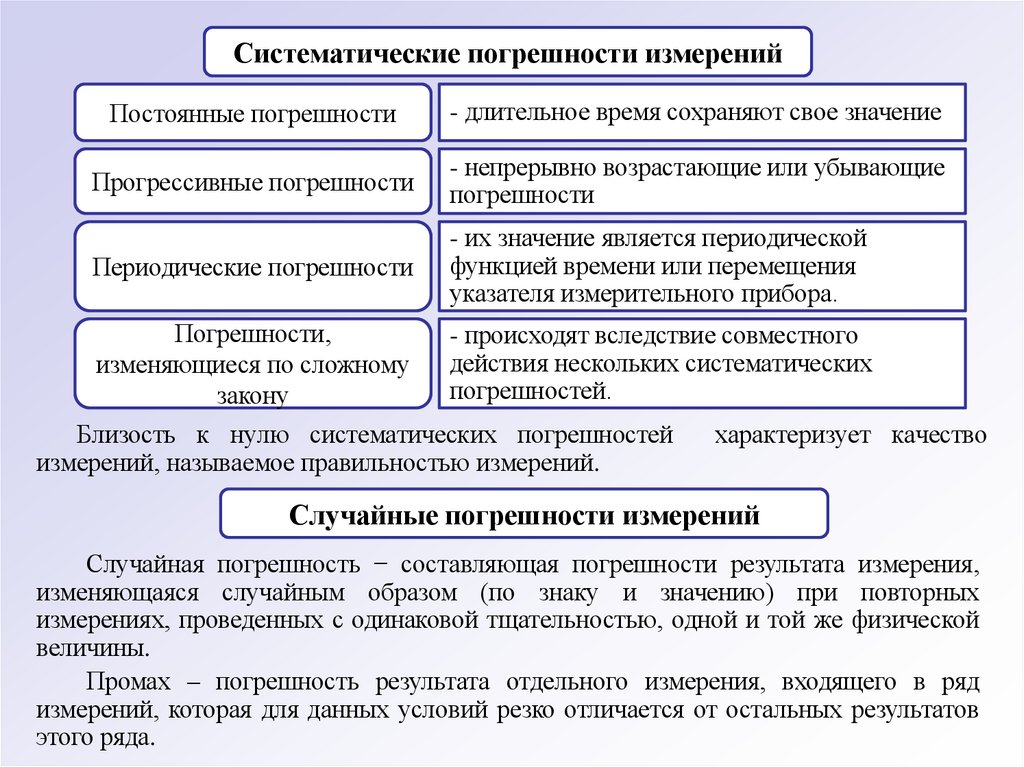
Систематические погрешности измерений
Постоянные погрешности
- длительное время сохраняют свое значение
Прогрессивные погрешности
- непрерывно возрастающие или убывающие
погрешности
Периодические погрешности
- их значение является периодической
функцией времени или перемещения
указателя измерительного прибора.
Погрешности,
изменяющиеся по сложному
закону
- происходят вследствие совместного
действия нескольких систематических
погрешностей.
Близость к нулю систематических погрешностей
измерений, называемое правильностью измерений.
характеризует качество
Случайные погрешности измерений
Случайная погрешность − составляющая погрешности результата измерения,
изменяющаяся случайным образом (по знаку и значению) при повторных
измерениях, проведенных с одинаковой тщательностью, одной и той же физической
величины.
Промах – погрешность результата отдельного измерения, входящего в ряд
измерений, которая для данных условий резко отличается от остальных результатов
этого ряда.

6.

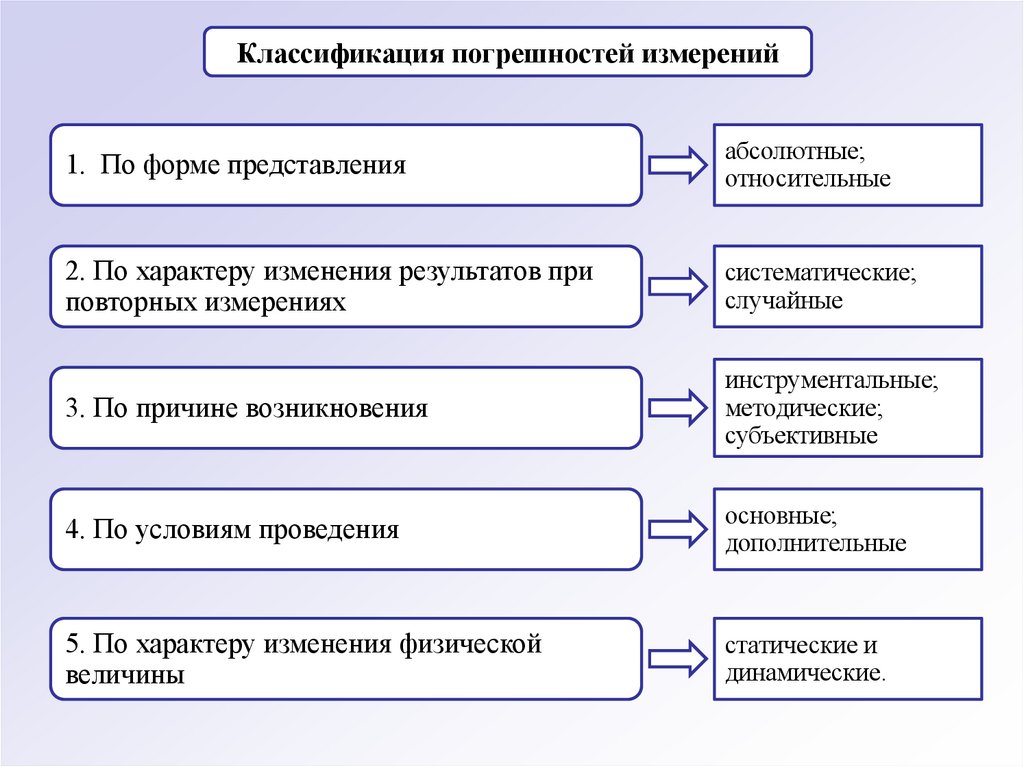
Классификация погрешностей измерений
1. По форме представления
абсолютные;
относительные
2. По характеру изменения результатов при
повторных измерениях
систематические;
случайные
3. По причине возникновения
инструментальные;
методические;
субъективные
4. По условиям проведения
основные;
дополнительные
5. По характеру изменения физической
величины
статические и
динамические.

7.

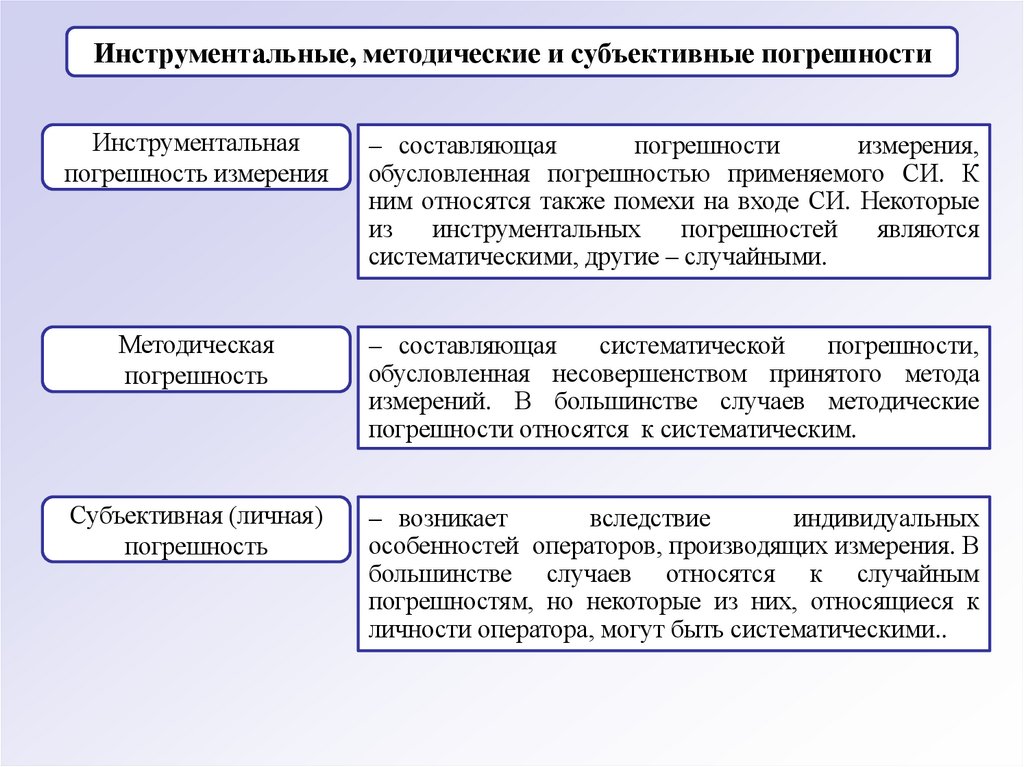
Инструментальные, методические и субъективные погрешности
Инструментальная
погрешность измерения
– составляющая
погрешности
измерения,
обусловленная погрешностью применяемого СИ. К
ним относятся также помехи на входе СИ. Некоторые
из
инструментальных
погрешностей
являются
систематическими, другие – случайными.
Методическая
погрешность
– составляющая
систематической
погрешности,
обусловленная несовершенством принятого метода
измерений. В большинстве случаев методические
погрешности относятся к систематическим.
Субъективная (личная)
погрешность
– возникает
вследствие
индивидуальных
особенностей операторов, производящих измерения. В
большинстве случаев относятся к случайным
погрешностям, но некоторые из них, относящиеся к
личности оператора, могут быть систематическими..

8.

Классификация погрешностей измерений
1. По форме представления
абсолютные;
относительные
2. По характеру изменения результатов при
повторных измерениях
систематические;
случайные
3. По причине возникновения
инструментальные;
методические;
субъективные
4. По условиям проведения
основные;
дополнительные
5. По характеру изменения физической
величины
статические и
динамические.

9.

Критерии качества измерений
Сходимость результатов
измерений
– близость друг к другу результатов измерений одной
и той же величины, выполненных повторно одними и
теми же средствами, одним и тем же методом в
одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость
результатов измерений
– близость результатов измерений одной и той же
величины, полученных в разных местах, разными
методами, разными средствами, разными операторами,
в разное время, но приведенных к одним и тем же
условиям измерений (температуре, влажности и др.).
Погрешность измерения
– отклонение результата измерения от истинного
(действительного) значения измеряемой величины.
Точность результата
измерений
– одна из характеристик качества измерения,
отражающая близость к нулю погрешности результата
измерения.
Правильность измерений
– качество измерений, отражающее близость к нулю
систематических
погрешностей
в
результатах
измерений.
Достоверность
измерений
– степень доверия к результатам измерений.

10.

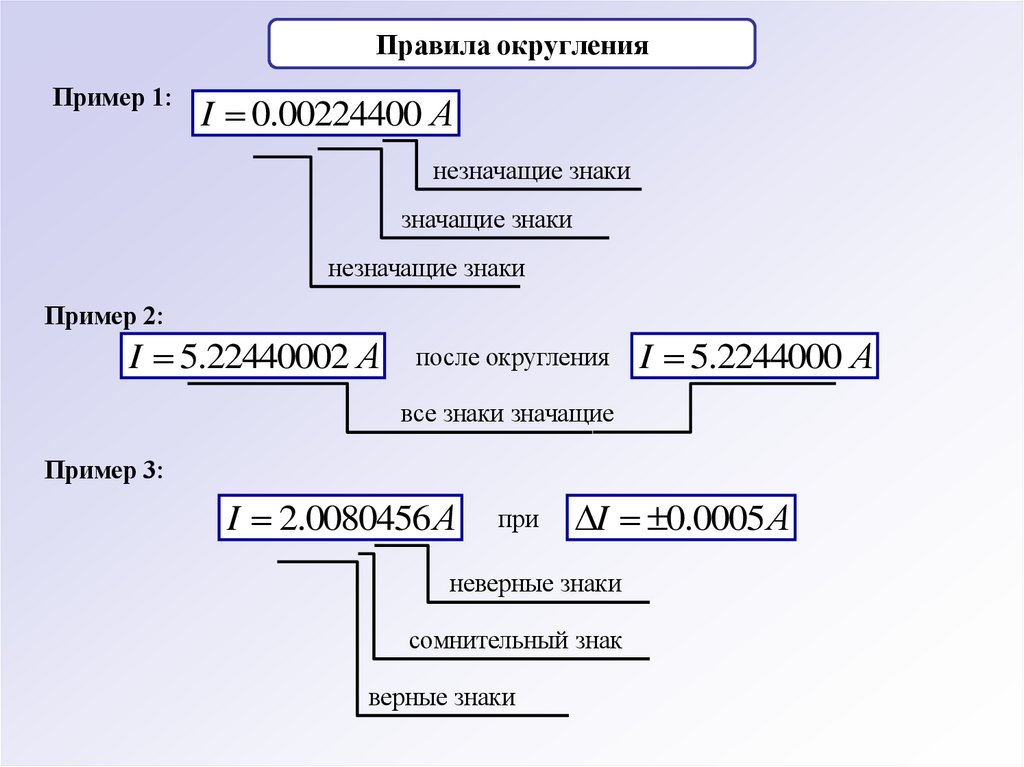
Правила округления
Пример 1:
I 0.00224400 А
незначащие знаки
значащие знаки
незначащие знаки
Пример 2:
I 5.22440002 А
после округления
I 5.2244000 А
все знаки значащие
Пример 3:
I 2.0080456 А
при
I 0.0005 А
неверные знаки
сомнительный знак
верные знаки

11.

Правила округления
1. Погрешность результата измерения указывается двумя значащими цифрами,
если первая из них равна 1 или 2, и одной – если первая цифра 3 или более.
2. Результат измерения округляется до того же десятичного знака, которым
оканчивается округленное значение абсолютной погрешности. Если десятичная
дробь в числовом значении результата измерений оканчивается нулями, то нули
отбрасываются до того разряда, который соответствует разряду числового значения
погрешности.
3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные
цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а
в десятичных дробях отбрасываются.
4. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней
следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают
на единицу.
5. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или
нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и
увеличивают на единицу, если она нечетная.
6. Округление производится лишь в окончательном ответе, а все
предварительные вычисления проводят с одним-двумя лишними знаками.

12.

Правила округления
Примеры
До округления
После округления
U = 27, 67185 В
U = 27, 67 В
U= ± 0,0591 В
U= ± 0,06 В
U = 27, 67185 В
U = 27, 672 В
U= ± 0,0291 В
U= ± 0,029 В
U = 27, 15095 В
U = 27, 2 В
U= ± 0,4501 В
U= ± 0,5 В

13. Случайные погрешности. Функции распределения случайных погрешностей.

Случайная погрешность - составляющая погрешности результата
измерения, изменяющаяся случайным образом (по знаку и значению)
при повторных измерениях, проведенных с одинаковой
тщательностью, одной и той же физической величины.
Наиболее универсальный способ описания случайных величин
заключается в отыскании их интегральных или дифференциальных
функций распределения.
Под интегральной функцией распределения результатов
наблюдений понимают вероятность того, что результат наблюдения
Хi в i-м опыте окажется меньшим некоторого текущего значения х: т.е.
Fx (x) = Р (Хi x)=P (- Xi x).
Если рассматривать результат отдельного наблюдения Хi
как
случайную точку на оси Ох, то значение интегральной функции
распределения в точке х численно равно вероятности того, что
случайная т. Хi в рез-те i-го измерения займет некоторое положение
левее т. х . При перемещении т. х в диапазоне от - до +
вероятности того, что т. Хi займут положения левее т. х будут
изменяться от 0 до 1.
0 Хi
х

14.

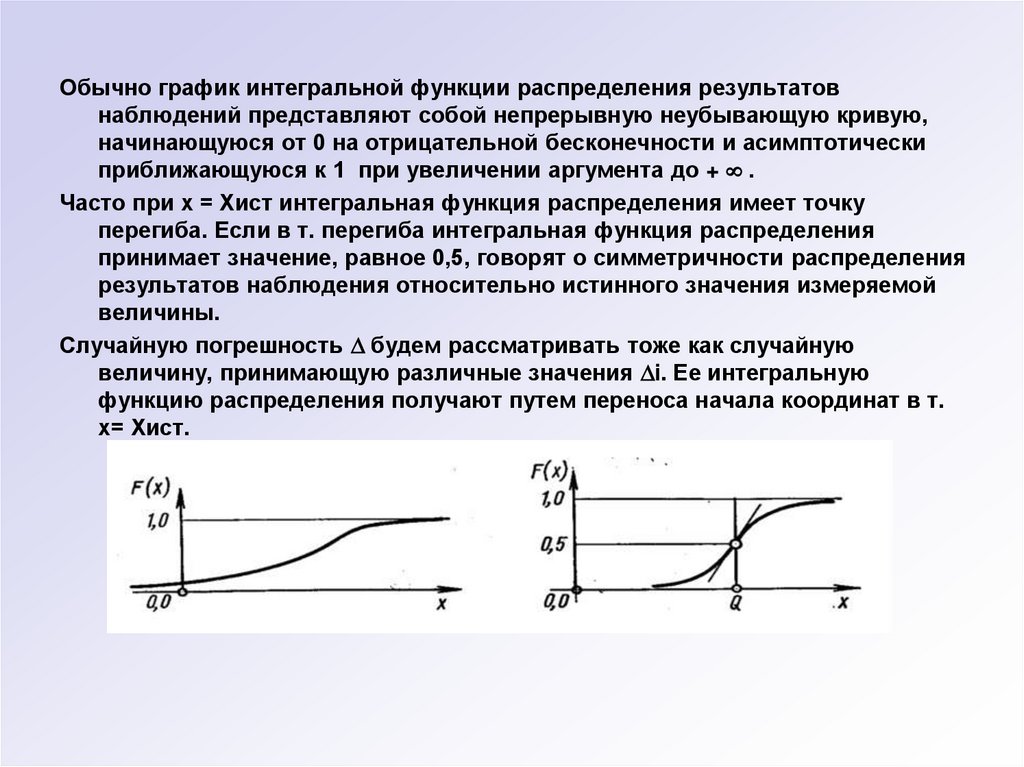
Обычно график интегральной функции распределения результатов
наблюдений представляют собой непрерывную неубывающую кривую,
начинающуюся от 0 на отрицательной бесконечности и асимптотически
приближающуюся к 1 при увеличении аргумента до + .
Часто при х = Хист интегральная функция распределения имеет точку
перегиба. Если в т. перегиба интегральная функция распределения
принимает значение, равное 0,5, говорят о симметричности распределения
результатов наблюдения относительно истинного значения измеряемой
величины.
Случайную погрешность будем рассматривать тоже как случайную
величину, принимающую различные значения i. Ее интегральную
функцию распределения получают путем переноса начала координат в т.
х= Хист.
F ( ) = Р ( i )=P (Xi – Хист х - Xист)= Р (Хi x)

15.

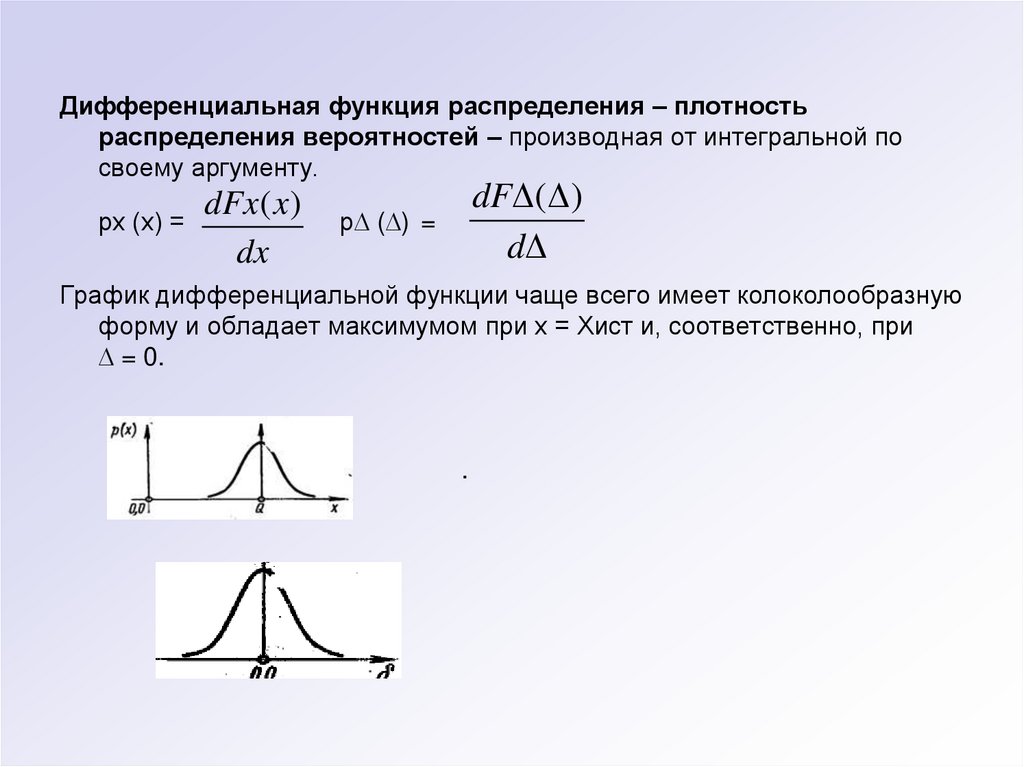
Дифференциальная функция распределения – плотность
распределения вероятностей – производная от интегральной по
своему аргументу.
dFx( x )
рх (х) =
dx
dF ( )
d
р ( ) =
График дифференциальной функции чаще всего имеет колоколообразную
форму и обладает максимумом при х = Хист и, соответственно, при
= 0.
.

16.

От дифференциальной функции распределения легко перейти к
интегральной путем интегрирования
F ( ) = p ( ) d
Поскольку Fx(+ ) = 1, то справедливо равенство:
p ( )d = 1,
Площадь, заключенная между кривой дифференциальной
функции распределения и осью абсцисс, равна 1.
Используя термины функций распределения, можно получить
выражения для вероятностей того, что результат наблюдения Х или
случайная погрешность примет при проведении измерения
некоторое значение в интервале 1; 2 .
В терминах интегральной функции распределения имеем:
Р( 1 2) = F ( 2) - F ( 1), т.е вероятность попадания случайной
погрешности в заданный интервал равна разности значений функции
распределения на границах этого интервала.

17. т

В терминах дифференциальной функции распределения :
Р( 1 2) =
2
p ( )d
1
Вероятность попадания случайной погрешности в заданный интервал
равна площади, ограниченной кривой распределения, осью абсцисс и
перпендикулярами к ней на границах этого интервала.
Т.о. результаты наблюдений в значительной степени
сконцентрированы вокруг истинного значения измеряемой величины, и
по мере приближения к нему элементы вероятности их появления
возрастают. Это дает основание принять за оценку истинного значения
измеряемой величины координату центра тяжести фигуры,
образованной осью абсцисс и кривой распределения, и называемую
математическим ожиданием результатов наблюдений:
М Х = mx =
xpx( x)dx
В эт. сл. случае систематической погрешностью является отклонение
математического ожидания результатов наблюдений от истинного
значения измеряемой величины. сист = М(Х)-хист
а случайной погрешностью – разность между результатом единичного
измерения и математическим ожиданием результатов с= Х-М(Х)

18. Моменты случайных погрешностей

Математическое ожидание погрешности измерения М( )= сист
обусловлено влиянием на него факторов, воздействующих на него
вполне определенным образом. Причины этих воздействий могут быть
установлены и в большинстве случаев устранены, например
введением поправок при измерении. Математическое ожидание не
определяет степень рассеивания возможных значений погрешности
около среднего значения.
Для оценки свойств законов распределения и полной характеристики
распределения результатов измерения или погрешности измерений
применяют числовые характеристики, называемые моментами.
Различают начальные моменты, найденные без исключения
систематической составляющей, и центральные моменты.
Т.о. начальный момент r-го порядка случайной величины определяется
r
X
формулой r= M( ). Начальный момент нулевого порядка равен 1,
а начальный момент первого порядка равен математическому
ожиданию случайной величины.
Центральные моменты характеризуют случайную величину (погрешность)
за вычетом систематической составляющей, т.е. становятся
центрированными.

19. Моменты случайных погрешностей

Центральным моментом r-го порядка результатов наблюдений
называется интеграл вида
r Х = ( x mx) px( x)dx = М ( X mx)
r
r
Особое значение наряду с математическим ожиданием результатов
наблюдений имеет второй центральный момент, называемый
дисперсией распределения результатов наблюдений.

20.

D Х = D = M ( X mx) = M 2 = p( )d
2
2
Дисперсия распределения случайной погрешности
равна
дисперсии распределения результатов наблюдений и является
характеристикой их рассеивания относительно математического
ожидания. Дисперсия имеет размерность квадрата измеряемой
величины. Чаще используется положительное значение корня
квадратного из дисперсии – среднее квадратическое отклонение
результатов наблюдений.
õ D X
Математическое ожидание и дисперсия являются наиболее
часто применяемыми моментами, поскольку определяют
наиболее важные черты распределения: положение центра
распределения и степень его разбросанности. Для более
подробного описания распределения используются моменты
более высоких порядков.

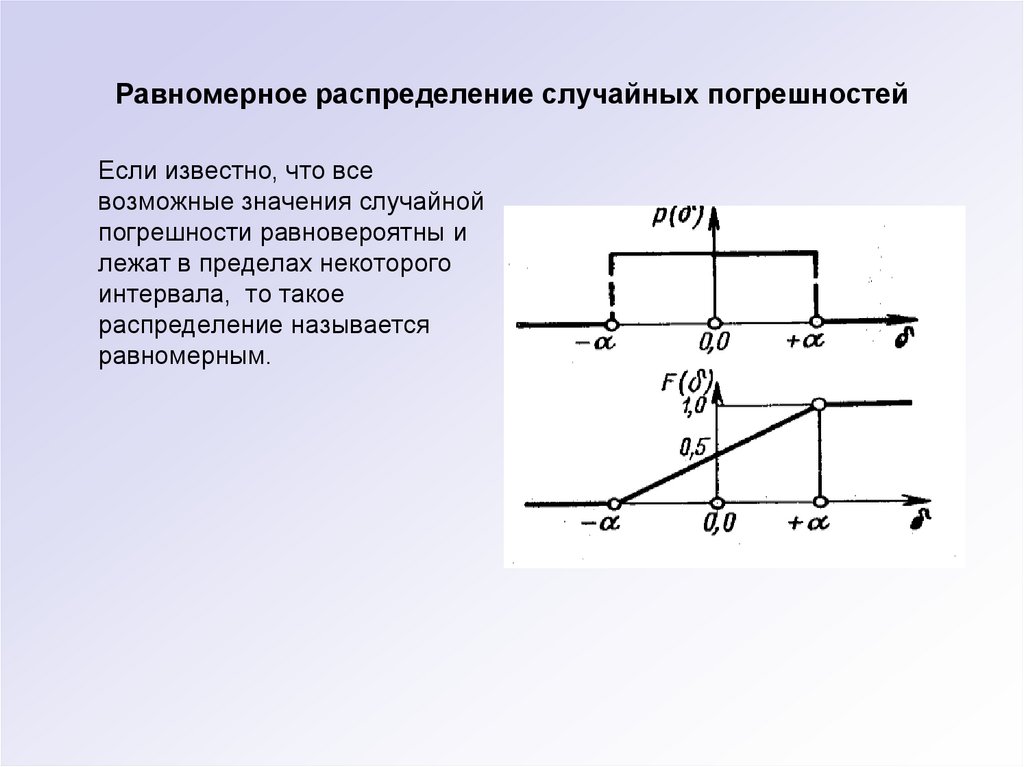
21. Равномерное распределение случайных погрешностей

Если известно, что все
возможные значения случайной
погрешности равновероятны и
лежат в пределах некоторого
интервала, то такое
распределение называется
равномерным.

22. с

Значения дифференциальной функции распределения равномерно
распределенной случайной погрешности в интервале - ;
постоянны, а вне этого интервала равны 0. Выражение для
дифференциальной функции распределения случайной погрешности
можно записать в виде:
Величину с находят из условия, что площадь, заключенная между
кривой распределения и осью абсцисс равна 1:
Среднее квадратическое отклонение случайной равномерно
распределенной погрешности равно:

23. Нормальный закон распределения случайных погрешностей

Дифференциальная функция для случайных погрешностей ,
распределенных по нормальному закону, имеет вид:
1
pΔ(Δ)= 2
2
2 2
*е
Для дифференциальной функции распределения результатов
измерений это распределение приобретает вид:
( x mx ) 2
pХ (х) =
1
x 2
ожидание;
*
е
2 x 2
, где mx – математическое
х – среднее квадратическое отклонение результатов
наблюдений.

24.

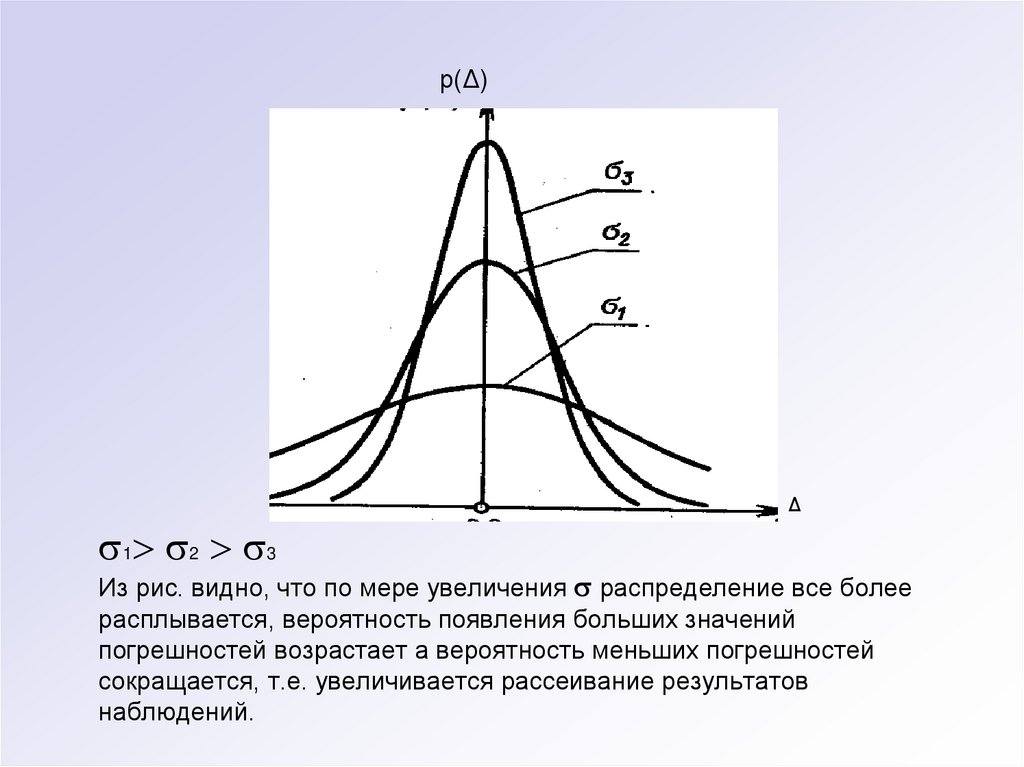
р(Δ)
Δ
1 2 3
Из рис. видно, что по мере увеличения распределение все более
расплывается, вероятность появления больших значений
погрешностей возрастает а вероятность меньших погрешностей
сокращается, т.е. увеличивается рассеивание результатов
наблюдений.

25.

При большом числе измерений вероятность появления случайных
погрешностей в большинстве случаев подчиняется нормальному
закону, симметричному относительно точки, соответствующей
максимальной плотности вероятности. Эта точка соответствует
истинному (среднему) значению измеряемой величины.
Если перенести ось ординат в точку математического ожидания, то это
будет кривая распределения случайных погрешностей.
Кривые распределения симметричны относительно оси ординат т.е.
появление равных по значению, но противоположных по знаку
случайных погрешностей имеют одинаковую вероятность. В средней
части кривые образуют выпуклость, по обе стороны от которой
находятся т. перегиба, ниже которых кривые становятся вогнутыми.
Наибольшая плотность вероятности соответствует случайной
погрешности, равной 0. При возрастании погрешности с любым знаком
вероятность ее появления уменьшается.
Промежутки между т. перегиба и осью ординат равны среднему
квадратическому отклонению, характеризующему степень рассеивания
значений случайных погрешностей от оси ординат.

26.

Чем меньше значение
, тем чаще наблюдаются малые случайные
погрешности и тем выше точность измерения. При больших значениях
большие случайные погрешности наблюдаются значительно чаще и
точность измерений снижается.
В теоретическом ур-ии плотности вероятности нормально
распределенной случайной погрешности значение Δ неизвестно, т.к.
Хист определить невозможно. По этой причине нельзя рассчитать и
Для устранения неопределенности значений Δ и
рекомендуют за
наиболее вероятное значение измеряемой величины принимать такое
ее значение, при котором сумма квадратов абсолютных погрешностей
минимальна. Т.о. наиболее вероятным значением измеряемой
величины будет среднее арифметическое ряда ее измерений.
В этом случае оценку
вычисляют по формуле =
1 n
2
( i)
n 1 1

27.

Среднее арифметическое представляет собой лишь оценку
математического ожидания результата измерения и может стать
оценкой истинного значения измеряемой величины лишь после
исключения систематических погрешностей.
Среднее арифметическое, полученное в одной из серий измерений,
является случайным приближением к Хист; чтобы иметь
представление о возможных отклонениях среднего арифметического
от Хист., необходимо определить его среднеквадратическое
отклонение.

28. Точечные оценки истинного значения измеряемой величины

В результате проведения измерений невозможно определить
истинное значение измеряемой величины, можно лишь с
большей или меньшей уверенностью оценить это значение.
Оценка истинного значения проводится по данным ряда
значений, принимаемых случайной величиной в процессе
независимых измерений. Основными параметрами функции
распределения случайной величины Х являются
математическое ожидание М Х = mх и дисперсия D Х = Dx.
Точечными оценками этих параметров называются оценки,
выражаемые одним числом.

29. Оценка результата измерения и его среднеквадратического отклонения

Для удобства анализа предположим, что при выполнении n
многократных наблюдений одной и той же величины Хи (сопротивление
резистора) постоянная систематическая погрешность Δс полностью
исключена.
Xi 20,500 20,380 20,400 20,330 20,610 20,450 20,400 20,600 20,300 20,550
Результат i-го наблюдения Хi = Xи + Δi находится с некоторой
абсолютной случайной погрешностью Δ = Xi − Xи
При нормальном законе распределения погрешности Δi за истинную
величину Хи = А принимают ее оптимальную оценку в виде среднего
арифметического значения (оценки математического
ожидания) выполненного ряда наблюдений, то есть считают, что
X = A есть результат измерения:
Зная оценку Xср истинного значения величины Xи, вычисляют
абсолютную погрешность каждого из n наблюдений Δ=Хи-Хср

30.

Пример.
Xi 20,500 20,380 20,400 20,330 20,610 20,450 20,400 20,600 20,300 20,550
Xср 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452
Δ
0,048 -0,072 -0,052 -0,122 0,158 -0,002 -0,052 0,148 -0,152 0,098
Далее находится оценка среднеквадратического отклонения σ наблюдений,
характеризующая точность метода измерений:
σ=
1 n
2
( i) = 0,109219
n 1 1
Оценка Xср = Aср измеряемого истинного значения Хи = А зависит от числа
наблюдений n и является случайной величиной. В связи с этим вводят и
вычисляют оценку среднеквадратического отклонения (СКО) значения
Xср = Aср , которая называется СКО результата измерения S(A)
Данное СКО характеризует степень разброса значений Xср = Aср по
отношению к истинному значению и для различных n определяется по
формуле:
σср = S(Aср) =
= 0,034538
n
Из выражений σ и σср = S(Aср) следует, что точность метода и результата
многократных наблюдений n увеличивается с ростом числа последних

31. Оценка с помощью интервалов

Наряду с точечными применяются интервальные оценки числовых
характеристик случайных величин, выражающиеся границами
интервала, внутри которого с определенной вероятностью заключено
истинное значение результата измерений.
Вероятность того, что результаты измерения не выйдут за границы какоголибо интервала погрешностей, определяется по площади,
ограниченной кривой распределения и границами этого интервала,
отложенными по оси абсцисс. Такой интервал называют
доверительным, а соответствующую ему вероятность появления
случайной погрешности (заштрихованная площадь) – доверительной
вероятностью. Нижнюю и верхнюю границы доверительного интервала
называют доверительными границами.

32.

Доверительный интервал обычно выражают через относительную
величину t в долях среднего квадратического отклонения
tp =
х
При нормальном распределении результатов наблюдений и
известном истинное значение измеряемой величины Хист с
доверительной вероятностью Р находится между границами
доверительного интервала Х - tp x ; Х + tp x
P(X- tp x ≤ Хист ≤ Х + tp x)

33.

Проведение многократных наблюдений позволяет значительно сократить
доверительный интервал. Если результаты наблюдений Xi (i=1,2,..n)
распределены нормально, то доверительный интервал, построенный с
помощью среднего арифметического n независимых повторных
наблюдений в n раз короче интервала, вычисленного по результату
одного наблюдения, хотя их доверительная вероятность одинакова.
Это говорит о том, что сходимость измерений растет пропорционально
корню квадратному из числа наблюдений.
х
Половина длины нового доверительного интервала =tp
n
называется доверительной границей погрешности результата
___
измерений, итог измерений записывается в виде: Х=
Х (Р= )

34.

Вычислим вероятность попадания результата наблюдения в некоторый
заданный интервал х1; х2 :
õ ( x 2mx)
1
P(x1 X x2) = ðõ( õ)dx =
e 2
dx
õ
2
x
1
õ
Сделав замену переменных
õ
2
2
1
x mx t
x
, получим P(x1 X x2) =
1 t t2
dt
e
2 t
2
1
2
t
1
Интеграл не выражается с помощью элементарных функций, его
вычисляют с помощью так называемого нормированного нормального
распределения с дифференциальной функцией
Интегральная функция этого распределения имеет вид
С помощью функции Ф(z) находят
вероятность
P(x1 X x2 ) = Ф(t2) – Ф(t1) = Ф(
x mx)
2
x
- Ф(
x mx
1
x
)

35. Интеграл Лапласа

36.

37.

38.

При малом числе повторных измерений используют распределение
случайных погрешностей, предложенное Стьюдентом. Плотность
вероятности по этому закону зависит не только от значения случайной
погрешности, но и от числа измерений n.
где
- плотность распределения вероятности случайной
погрешности при заданном числе измерений;
Г(n)- гамма-функция, значение которой зависит от числа измерений и
обладающая свойством Г(n+1)= n- Г(n).
При большом числе проведенных измерений
распределение Стьюдента совпадает с
распределением по нормальному закону, а при
малом – резко отличается о нормального.

39.

40.

Необходимость многократных измерений некоторой физической
величины ХИ возникает при наличии в процессе измерений
случайных погрешностей. В этом случае задача состоит в том, чтобы по
результатам измерений найти наилучшую оценку истинного значения Хи и
интервал, в котором находится сама величина Хи с заданной
вероятностью. Решение задачи выполняется способом статистической
обработки результатов измерений, основанным на гипотезе о
распределении случайных погрешностей этих результатов по
нормальному закону. Методика обработки результатов измерений
используется применительно к прямым измерениям с многократными
независимыми и равноточными наблюдениями.
Точность результата многократных наблюдений тем выше, чем меньше
систематическая составляющая их погрешности. Поэтому весьма важно
выявление систематических погрешностей и исключение их из
результатов наблюдений. К числу мер такого исключения относятся:
• устранение источников погрешностей до начала измерения;
• устранение (уменьшение) погрешностей в процессе измерения за счет
использования соответствующих методов измерения.

41. Грубые погрешности

Промах (грубая погрешность) – погрешность результата отдельного
измерения, входящего в ряд измерений, которая для данных условий
резко отличается от остальных результатов этого ряда.
Обычно грубая погрешность следствием значительного изменения
условий эксперимента; «броски» тока источника электропитания, не
учтенное экспериментатором изменений окружающей температуры,
неправильный отсчет показаний СИ. Т.к. грубые погрешности
относятся к случайным, для их выявления и исключения используются
методы теории вероятностей (методы проверки гипотез).
Один из критериев отнесения результата измерений к промахам:
если случайные отклонения результата наблюдения превышают 4 , то
данное наблюдение – промах. Этот критерий основывается на том, что
вероятность появления погрешности 4 при нормальном
распределении равна 0,000064, вследствие чего является
маловероятной и не характерной для данного ряда наблюдений.
Проверяемая гипотеза состоит в утверждении, что некоторый результат
(как правило, наибольший или наименьший) не содержит грубой
погрешности.

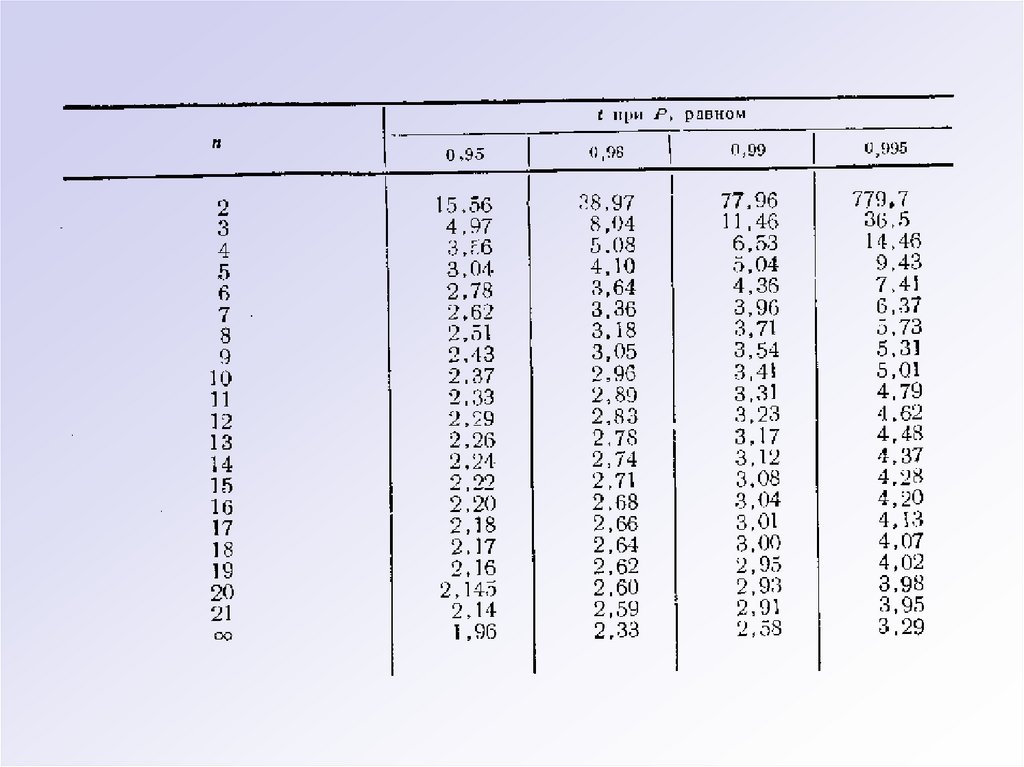
42.

Для оценки по этому критерию рассчитывают с выбранной
доверительной вероятностью Р и числа измерений n те наибольшие
значения критерия tд и сравнивают с ним расчетное значение t,
которые он может принимать по чисто случайным причинам. При t tд
результат измерений относят к грубым.

43.

44. Пример

Xi 20,500 20,380 20,400 20,330 20,610 20,450 20,400 20,600 20,300 20,550
X~ 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452 20,452
=0,109219
При измерении физической величины (сопротивление резистора)
среди результатов наблюдений могут появиться одно-два,
существенно отличающихся от остальных. При этом необходимо
проверить, не являются ли они грубыми погрешностями (промахами),
которые следует исключить из выполненной группы наблюдений. Для
этого проводят следующие операции.
Результаты группы из n наблюдений упорядочивают по возрастанию
Х1 ≤ Х2 ≤ …≤ Хn.
Xi 20,300 20,330 20,380 20,400 20,400 20,450 20,500 20,550 20,600 20,610
По приведенным формулам вычисляются оценки среднего
арифметического значения X и СКО наблюдений σ данной выборки. Для
предполагаемых промахов, которыми могут быть Х1 и Х10,
рассчитываются коэффициенты t1=1,391693 и t10=1,446629.

45. Систематические погрешности

Систематическая погрешность измерения – составляющая
погрешности результата измерения, остающаяся постоянной или
закономерно изменяющаяся при повторных измерениях одной и той же
физической величины.
В зависимости от характера измерения систематические погрешности
подразделяют на постоянные, прогрессивные, периодические и
погрешности, изменяющиеся по сложному закону.
Постоянные погрешности – погрешности, которые длительное время
сохраняют свое значение, например, в течение времени выполнения
всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности – непрерывно возрастающие или
убывающие погрешности. К ним относятся, например, погрешности
вследствие износа измерительных наконечников, контактирующих с
деталью при контроле ее прибором активного контроля.
Периодические погрешности – погрешности, значение которых
является периодической функцией времени или перемещения
указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят
вследствие совместного действия нескольких систематических
погрешностей.

46.

По причинам возникновения их делят на инструментальные,
субъективные, погрешности метода, погрешности установки
Инструментальная погрешность измерения – составляющая
погрешности измерения, обусловленная погрешностью применяемого
средства измерений.
Погрешность метода измерений – составляющая систематической
погрешности измерений, обусловленная несовершенством принятого
метода измерений. Погрешность метода иногда называют
теоретической погрешностью.
Погрешность (измерения) из-за изменений условий измерения –
составляющая систематической погрешности измерения,
являющаяся следствием неучтенного влияния отклонения в одну
сторону какого-либо из параметров, характеризующих условия
измерений, от установленного значения. Этот термин применяют в случае
неучтенного или недостаточно учтенного действия той или иной
влияющей величины (температуры, атмосферного давления, влажности
воздуха, напряженности магнитного поля, вибрации и др.); неправильной
установки средств измерений, нарушения правил
их взаимного расположения и др.

47.

Субъективная погрешность измерения – составляющая
систематической погрешности измерений, обусловленная
индивидуальными особенностями оператора.

48. Методы исключения систематических погрешностей

Методы устранения систематических погрешностей: метод
замещения, симметричных наблюдений и компенсации по
знаку.
Метод замещения состоит в такой замене измеряемой величины Хи
известной величиной А (мерой), получаемой с помощью регулируемой
меры, чтобы показание измерительного прибора сохранилось
неизменным. Значение измеряемой величины считывается в этом
случае по указателю меры.
При данном методе погрешность недостаточно точного измерительного
прибора устраняется, а погрешность измерения определяется только
погрешностью самой меры и погрешностью отсчета измеряемой
величины по указателю меры.
Пример: измерялось сопротивление резистора Rх омметром
малой точности. Результат измерения равен Х = Rх+Δс, где Х и Δс –
соответственно показание омметра и систематическая погрешность
измерения. Заменив Rх магазином сопротивлений и отрегулировав
его так, чтобы сохранилось показание омметра, получим Х = Rм+Δс.
Их приведенных двух выражений для Х следует, что Rх = Rм.

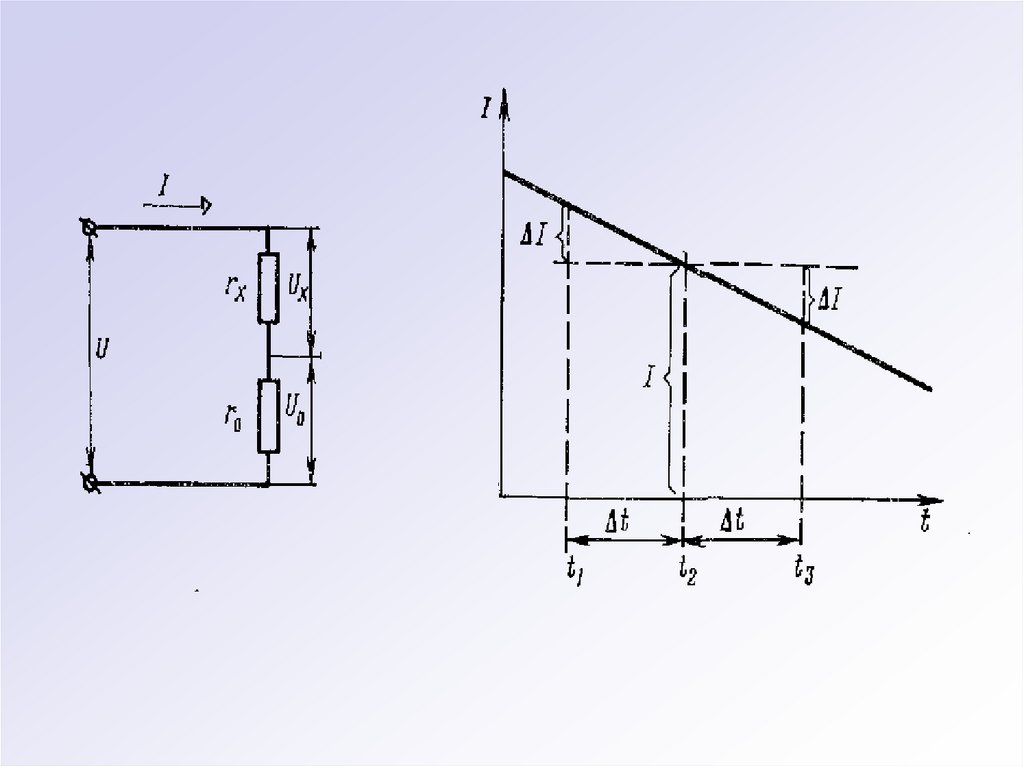
49.

50.

Способ симметричных наблюдений оказывается весьма
эффективным при исключении прогрессивной погрешности,
являющейся линейной функцией соответствующего аргумента
(амплитуды напряжения, времени, температуры и т.д.).
Измерения проводят последовательно через одинаковые
интервалы изменения аргумента, а обработку полученных
результатов осуществляют с учетом равенства среднего
значения погрешности любой пары симметричных наблюдений
погрешности, соответствующей средней точке данного
интервала. Подобным образом удается исключить погрешности
измерений, обусловленные постепенным падением уровня
напряжения источника питания (аккумулятора, батареи).

51.

52.

53.

54. Исключение систематических погрешностей путем введения поправок

Поправка Сj – величина, одноименная измеряемой, которая вводится в
результат измерения Xi = X ′i + θj + Cj с целью исключения
составляющих систематической погрешности θj. При Сj = – θj j-я
составляющая погрешности полностью устраняется из результата
измерения. Поправки определяются экспериментально или в
результате специальных теоретических исследований. Они задаются
в виде таблиц, графиков или формул.
В практических расчетах погрешность результата обычно выражается не
более чем двумя значащими цифрами, поэтому поправка, если она
меньше пяти единиц младшего разряда, следующего за последним
десятичным разрядом погрешности результата, все равно будет
потеряна при округлении и вводить ее не имеет смысла.

55.

Неисключенная систематическая погрешность результата образуется из
составляющих, в качестве которых могут быть неисключенные
систематические погрешности: метода, средств измерений, вызванные
другими источниками. В качестве границ составляющих
неисключенной систематической погрешности принимают, например,
пределы допускаемых основных и дополнительных погрешностей
средств измерений, если случайные составляющие погрешности
пренебрежимо малы.
При суммировании составляющих неисключенной систематической
погрешности результата измерения неисключенные систематические
погрешности средств измерений каждого типа и погрешности поправок
рассматривают как случайные величины. При отсутствии данных о
виде распределении случайных величин их распределения принимают
за равномерные.
Границы неисключенной систематической погрешности результата
измерения вычисляют путем построения композиции неисключенных
систематических погрешностей средств измерений, метода и
погрешностей, вызванных другими источниками. При равномерном
распределении неисключенных систематических погрешностей эти
границы (без учета знака) можно вычислить по формуле
=к
m
i 1
2
i

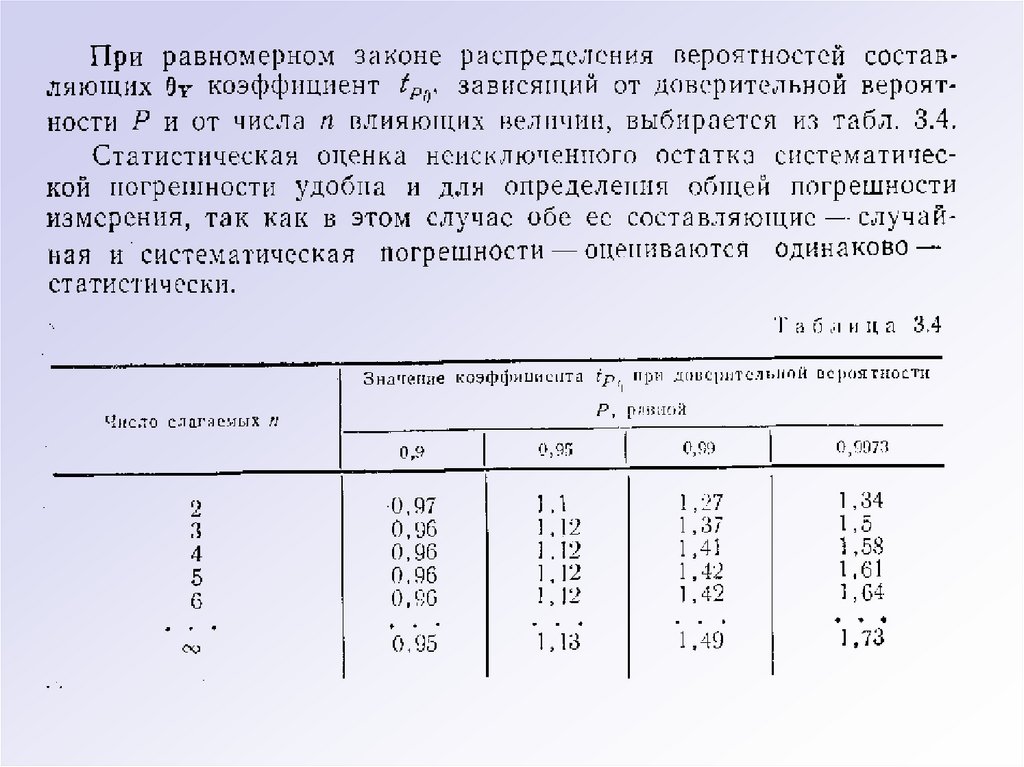
56.

где i – граница i-той неисключенной систематической погрешности;
К – коэффициент, определяемый принятой доверительной вероятностью.
Коэффициент к принимают равным 1,1 при доверительной
вероятности Р=0,95.
При доверительной вероятности Р=0,99 коэффициент К принимают
равным 1,4, если число суммируемых неисключенных погрешностей
более 4.

57.

58. Общая погрешность измерений

Общая погрешность результата измерений состоит из случайной
и систематической составляющих.

59.

60.

В случае, если
0,8, то систематическими погрешностями по
S сравнению со случайными пренебрегают и
считают, что погрешность результата измерений равна
8, то случайной погрешностью по сравнению с
S систематическими пренебрегают и считают, что
погрешность результата равна .
Если
В случае, если неравенства не выполняются, то погрешность
результата измерений находят путем построения композиции
распределений случайной и систематической погрешности,
рассматриваемых как случайные величины.

61. Проверка нормальности распределения результатов наблюдений

Сходимость результатов наблюдений можно оценить наиболее полно, если
их распределение является нормальным. Поэтому при обработке
результатов важную роль играет проверка нормальности
распределения.
При числе результатов наблюдений n 50 для проверки принадлежности
их к нормальному распределению является критерий 2 Пирсона.
Весь диапазон полученных результатов наблюдений Хmax – Хmin разделяют
на r интервалов шириной i и подсчитывают частоты mi, равные числу
результатов, лежащих в каждом i-том интервале.
Pi * mi , где n – общее число наблюдений, называют
частостями
n и представляют собой статистические оценки
Отношения
вероятностей попадания результата наблюдений в i-ый интервал.
Распределение частостей по интервалам образует статистическое
распределение результатов наблюдений. Разделив частость на длину
интервала, получим величины, являющиеся оценками средней
плотности распределения на интервале xi

62.

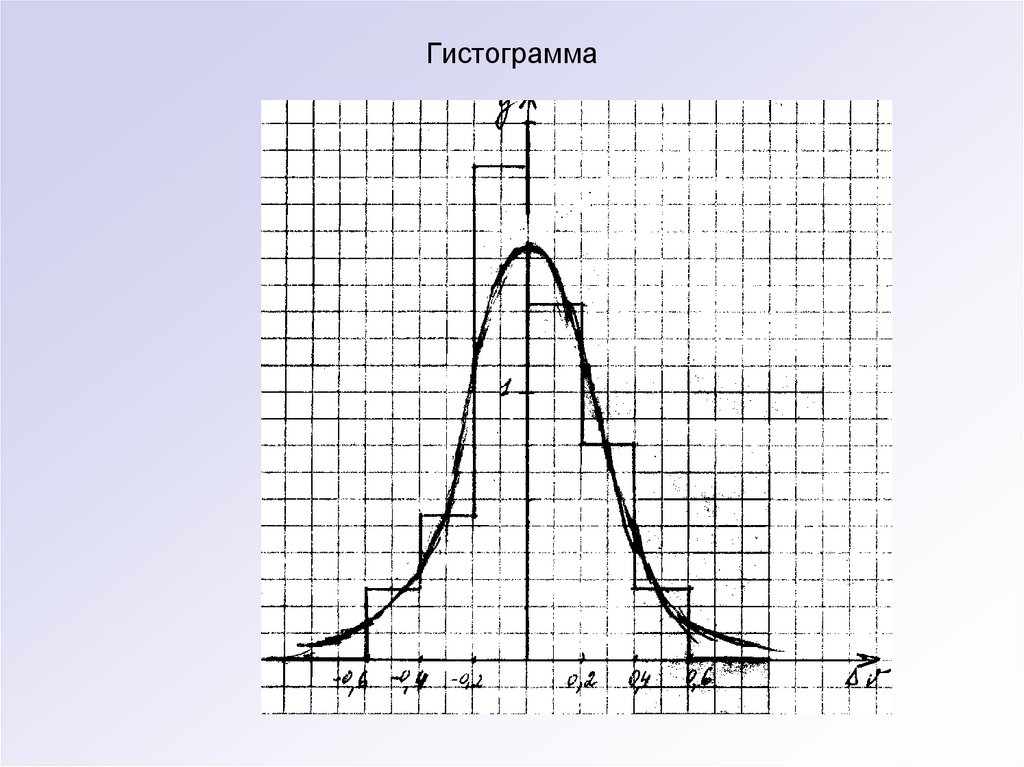
Вдоль оси результатов наблюдений отложим интервалы xi в порядке
возрастания индекса i и на каждом интервале построим прямоугольник
с высотой * Полученный график называется гистограммой
Pi распределения. Площадь всех прямоугольников равна
статистического
1
После построения гистограммы подбирают
теоретическую кривую распределения. Определение
теоретического вида кривой распределения сводится
к выбору таких значений его параметров, при которых
достигается наибольшее соответствие между теоретическим и
статистическим распределением.
При использовании метода моментов параметрам теоретического
распределения придают такие значения, при которых несколько
важнейших моментов совпадают с их статистическими оценками.
Если статистическое распределение, определяемое гистограммой, хотим
описать кривой нормального распределения, необходимо, чтобы
математическое ожидание и дисперсия совпали со средним
арифметическим и оценкой дисперсии, вычисленным экспериментальн

63.

Проверка нормальности распределения результатов измерений
проводится методом проверки статистических гипотез. На основании
гистограммы, полученной при обработке опытных данных, строится
гипотеза, состоящая в том, что результаты наблюдений подчиняются
распределению Fx(x) c плотностью pх(х).
Для того, чтобы опровергнуть или принять гипотезу, выбирается некоторая
величина U, представляющая собой меру расхождения теоретического
и статистического распределений. В качестве меры расхождения
можно принять сумму квадратов разностей частостей и теоретических
вероятностей попадания результатов наблюдений в каждый интервал,
взятых с некоторыми коэффициентами Сi, называемыми весами
r
2
разрядов
Мера расхождения U является случайной
*
U Ci ( Pi Pi )
величиной и подчиняется 2-распределению
i 1
с k степенями свободы. Число степеней свободы распределения k=r-s,
где r – число разрядов гистограммы статистического распределения, sчисло независимых связей, наложенных на частости.
Если проверяется гипотеза о нормальности распределения, то к числу
этих связей относится равенство среднего арифметического и точечной
оценки дисперсии соответственно математическому ожиданию и
дисперсии предполагаемого нормального распределения. Кроме того,

64.

требуется, чтобы сумма частостей по всем интервалам была равна 1.
поэтому в данном случае s=3.
Мера расхождения U, выбранная по Пирсону, обозначается
где
По данным таблицы 2 можно при заданной доверительной вероятности
=1-g тот доверительный интервал значений 2к,в который мера
расхождения может попасть по чисто случайным причинам.
Если вычисленная по опытным данным мера расхождения окажется в
указанном интервале, то гипотеза принимается. Это не значит, что
гипотеза верна. Можно лишь утверждать, что она правдоподобна. Если
2 выходит за границы доверительного интервала, то гипотеза
отвергается, как противоречащая опытным данным. Поскольку
гипотеза основывается на опытных данных, то при принятии решения
всегда возможны ошибки. Отвергая в действительности верую
гипотезу, мы совершаем ошибку первого рода. Вероятность ошибки
первого рода называется уровнем значимости и составляет g=1-

65.

Принимая в действительности неверную гипотезу, мы совершаем ошибку
второго рода. Вычислить ее вероятность, вообще говоря, невозможно.
Можно лишь утверждать, что при уменьшении ошибки первого рода,
ошибка второго рода увеличивается, поэтому не имеет смысла брать
слишком высокие значения доверительных вероятностей.
Описанная процедура проверки о том, что данное статистическое
распределение является распределением с плотностью рх(х)
называется критерием согласия 2.
При числе результатов наблюдений 50 n 15 для проверки
принадлежности их к нормальному распределению предпочтительным
является составной критерий, представленный в приложении 1 ГОСТ
8.207-76.
При числе результатов наблюдений n ≤ 15 принадлежность их к
нормальному распределению не проверяют.

66. Обработка результатов прямых измерений

При статистической обработке результатов наблюдений следует
выполнить следующие операции:

67. Случайные погрешности косвенных измерений

68.

69. Задача

Задача. При 19 измерениях сопротивления R катушки получены
результаты наблюдений Ri в омах, которые представлены в
таблице. Измерения проводились на мосте постоянного тока
Р3009 в нормальных условиях. Требуется определить
значение сопротивления катушки и погрешность измерения с
доверительной вероятностью Р=0,99.
n
Ri
R= n =
1
1001,10 1000,98 1000,92 ... 1000,28
19
=1000,58 Ом
Случайную составляющую погрешности результата
измерений определяют в последовательности:

70.

Ri
Vi
V2i
Ri
Vi
V2i
1001,10
+0,52
0,2704
1000,51
-0,07
0,0049
1000,98
+0,40
0,1600
1000,16
-0,42
0,1764
1000,92
+0,34
0,1156
1000,58
0
0
1000,56
-0,02
0,0004
1000.39
-0,19
0,0361
1000,80
+0,22
0,0484
1000,59
+0,01
0,0001
1000,55
-0,03
0,0009
1000,61
+0,03
0,0009
1000,54
-0,04
0,0016
1000,28
-0,30
0,0900
1000,04
-0,54
0,2916
1000,48
-0,10
0,0100
1000,65
+0,07
0,0049
1000,71
+0,13
0,0169
1000,57
-0,01
0,0001
n
R=1000,58
n
Vi =+1,72- V 2 i =1,2292
1
-1,72=0
1

71.

Для построения гистограммы:
количество частей g разделения диапазона погрешностей
при числе наблюдений 15 ≤ n ≤ 40 берут равным 6-8;
длины интервалов погрешностей выбирают одинаковыми;
масштабы по вертикальным и горизонтальным осям
гистограммы подбирают такими,, чтобы отношение ее высоты к
основанию было равным 5-8;
разобьем диапазон случайных отклонений (-0,54 ≤Vi ≤0,52) на
6 равных частей через промежутки v =0,2 и посчитаем число
положительных Zi и отрицательных Z1i отклонений,
приходящихся на каждую часть.
вычислим частоты Р*i и плотности частот уi появления
отклонений Vi по формулам
Zi
P*i =
n
р
i
и у=
i
vi

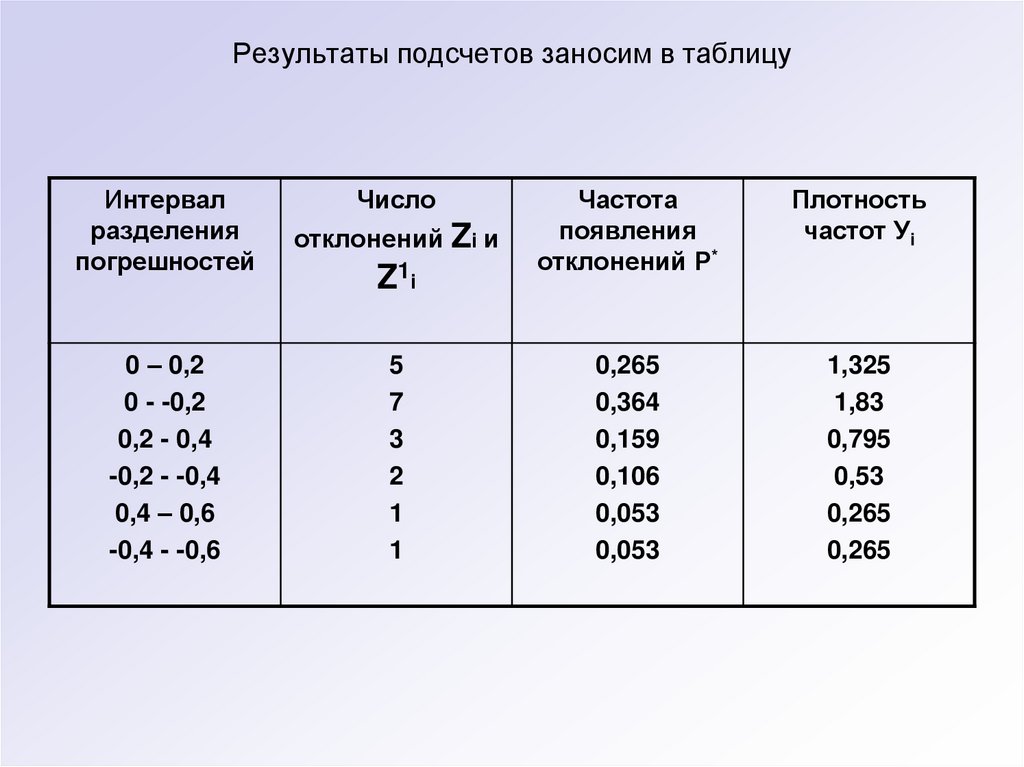
72. Результаты подсчетов заносим в таблицу

Интервал
разделения
погрешностей
Число
отклонений Zi и
0 – 0,2
0 - -0,2
0,2 - 0,4
-0,2 - -0,4
0,4 – 0,6
-0,4 - -0,6
5
7
3
2
1
1
Z1i
Частота
появления
отклонений Р*
Плотность
частот Уi
0,265
0,364
0,159
0,106
0,053
0,053
1,325
1,83
0,795
0,53
0,265
0,265

73. Гистограмма

74.

Среднее квадратическое значение случайных
погрешностей наблюдений
n
2
= n 1 =
1
i
1,2292
19 1
=0,2612 Ом
Среднее квадратическое случайной составляющей
погрешности результата измерения
S=
0,2612
19
=
=0,06190 Ом
n
Определим случайную составляющую
погрешности
результата измерений c=±tcS, tc=2,88 при n=19 и Р=0,99
c= ± 2,88*0,06190= ± 0,17827 Ом
Систематическая составляющая погрешности измерения
составляет 1000.58 * 0,01
= 0,1001 Ом
100

75.

Считая, что остатки систематических погрешностей в этих границах
распределены равномерно, то их среднее квадратическое
S=
0.1001
=
= 0,0577 Ом
3
3
Для определения общей погрешности находим отношение
= 0 ,1001 = 1,668
S 0 , 0619
Оно лежит в пределах от 0,8 до 8, поэтому пренебрегать ни одной из
составляющих общей погрешности нельзя.
Общая погрешность определяется по формуле
Среднее квадратическое общей погрешности
S = S 2 S 2 0,06192 0,0577 2 0,0846 Ом
Значение t P определим по формуле
=
0,1001 0,17827
=2,3276
0,0577 0,0619

76.

Общая погрешность измерения
=±2,3276*0,0846= ±0,1969 Ом= ±0,20 Ом
Результат измерения сопротивления на Р3009 может быть
записан в виде R=1000,58 ±0,20 (0,99) Ом

77. Методы проверки принадлежности случайных погрешностей к нормальному распределению

В соответствии с ГОСТ 8.207-76 при числе результатов наблюдений
15< n < 50 для проверки принадлежности их к нормальному
распределению предпочтительным является составной критерий,
приведенный в приложении 1

78.

79.

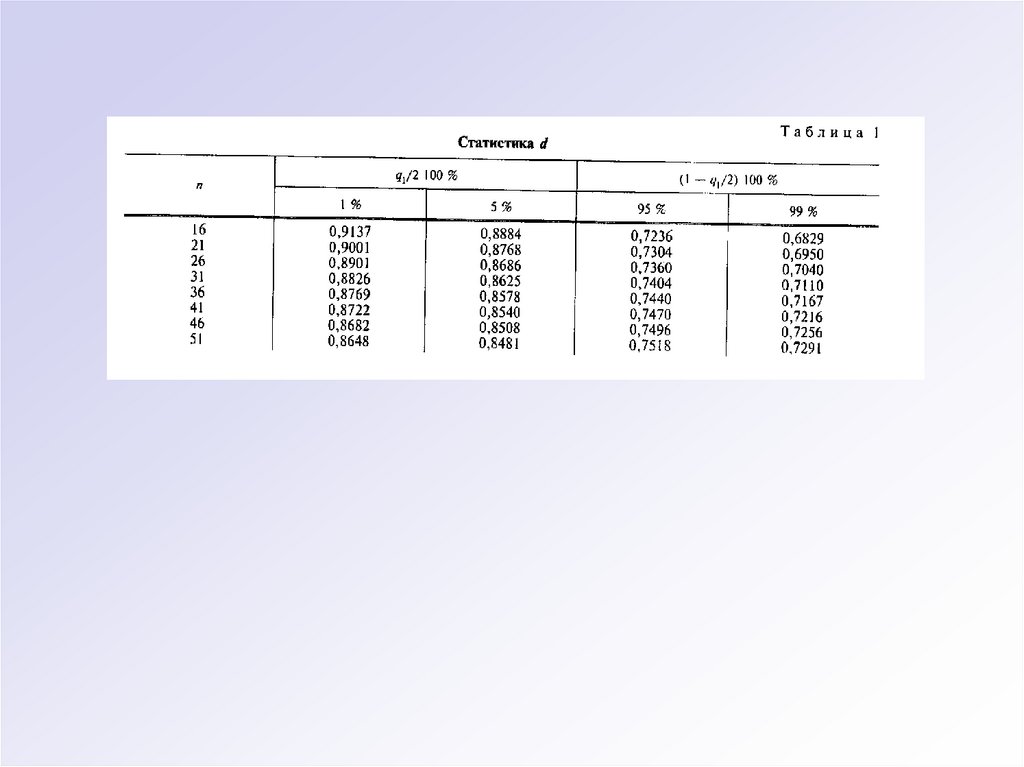
80. Проверка нормальности распределения

Критерий 1.
S*=
1,2238
0,254
19
1,72 1,72
d = 19 * 0,254 0,713
0,6902< d < 0,9055 - критерий 1 выполняется
Критерий 2.
S=0,26, при Р=0,99 ему соответствует Z=2,58
при Z*S=2,58*0,26=0,6708 не более 1 разности может выходить за
это значение. В нашем случае таких отклонений нет. Т.о. критерий 2
– выполняется.
Вывод – результаты наблюдений подлежат нормальному
распределению.
Если хотя бы один из критериев не выполняется, то распределение
результатов наблюдений не соответствует нормальному.

81. Измерения и неопределенность измерений

В Российской Федерации используются два подхода к
оцениванию точности измерений. Один подход, связанный с анализом
погрешностей, основан на понятиях и терминах, применяемых в
отечественных нормативных документах в области обеспечения
единства измерений, а в другом подходе для оценки точности
измерений используется относительно новый количественный
показатель — неопределенность. В течение длительного периода
времени понятия случайной и систематической погрешностей, а также
анализ погрешностей являлись практической частью метрологии.
Случайная погрешность измерения характеризовалась разностью
между результатом измерения и истинным значением измеряемой
величины, которое должно быть получено при идеальном измерении.
Однако истинное значение измеряемой величины является идеальным
понятием и не может быть точно известно. Поэтому погрешность тоже
не может быть точно известна. Практическая случайная погрешность
измерения часто оценивалась как разность между результатом
измерения исследуемой величины и средним значением, полученным
из повторных измерений. В настоящее время признано, что когда все
известные или ожидаемые составляющие погрешности оценены и
поправки учтены в результате измерения, то все еще остается
неопределенность в полученном результате, т.е. имеются сомнения
относительно того, как хорошо результат измерения представляет
значения измеренной величины.

82.

При определении значения измеряемой величины должны быть
указана лучшая оценка самой величины и оптимальная оценка ее
неопределенности.
Неопределенность результата измерения отражает
недостаток точного знания об измеряемой величине и определяется как
параметр, связанный с результатом измерения и характеризующий
рассеяние полученных значений, которые могут быть обоснованно
приписаны измеряемой величине.
Оценка неопределенности есть характеристика измерений,
которая должна быть легко реализуемой при обработке полученных
результатов, а также всеми признанной.
Оценка неопределенности зависит от детального знания
сущности природы измеряемой величины и непосредственно от
используемой процедуры измерения. В конечном итоге качество и
значимость полученной оценки неопределенности, которая
приписывается результатам измерений с учетом их расчетной обработки,
зависят в значительной степени от знаний, способности к критическому
анализу, компетентности исследователей, т. е. всех тех, кто участвует в
процессе измерения исследуемой величины и правильной интерпретации
результатов измерений

83. Показатели точности измерений

Повторяемость (результатов измерений) — степень близости между
результатами последовательных измерений одной и той же
измеряемой величины, выполненных в одинаковых условиях
измерений.
Эти условия называют условиями повторяемости (сходимости). Они
включают: одинаковую измерительную процедуру; одного оператора;
одинаковые средства измерений, используемые при одинаковых
условиях; одинаковое размещение; повторение в течение короткого
промежутка времени.
Повторяемость (сходимость) может быть выражена количественно в
виде характеристик рассеяния результатов.
Воспроизводимость (результатов измерений) — это степень
близости между результатами измерений одной и той же измеряемой
величины, выполненных в измененных условиях измерений.
Обоснованное утверждение воспроизводимости измерений требует
детализации измененных условий, а они могут включать: принцип
измерения; метод измерения; оператора; эталон; размещение; условия
использования средств измерений; время.
Воспроизводимость может быть выражена количественно в виде
характеристик рассеяния результатов, под которыми понимают
исправленные результаты.

84.

Воспроизводимость является характеристикой совместимости
лабораторий, занимающихся измерениями одной и той же величины
или характеристикой совершенства или несовершенства той или иной
методики измерений в условиях, когда измерения выполняются в
разных местах и, разумеется, разными лабораториями.
Введение неопределенности основано на непознаваемости истинного
значения величины и некорректности понятия «погрешность» на
соответствующей действительной процедуре измерения. В то же время
и неопределенность, и погрешность — это критерии качества
измерений, несущие одну и ту же информацию.
Таким образом, характеристики погрешности могут быть
выражены на языке определенности. Разумеется, что для них введены
соответствующие термины, что и сделано в концепции
неопределенности.
Результат оценки качества измерений, выполненной путем расчета,
называют неопределенностью измерений.

85.

Введение неопределенности основано на непознаваемости
истинного значения величины и некорректности понятия
«погрешность» на соответствующей действительной процедуре
измерения. В то же время и неопределенность и погрешность это критерии качества измерений, несущие одну и ту же
информацию. Т.о. характеристики погрешности могут быть
выражены на языке неопределенности. Для них введены
соответствующие термины.
Результат оценки качества измерений, выполненной путем
расчета, называют неопределенностью измерений.
«Руководство по выражению неопределенности измерения»
определяет этот термин как параметр, связанный с
результатом измерения, который характеризует
дисперсию значений, которые могли быть обосновано
приписаны измеряемой величине. Механизм этого расчета
заключается в том, что сначала проводят анализ
измеряемой величины, цель которого – определить
источники погрешности и создать модель измерения.

86.

В отличии от принятого деления погрешностей на случайные и
систематические на основе анализа их источников или причин
возникновения составляющие неопределенности группируют в
2 типа на основании метода их оценки. Это связано с тем, что в
зависимости от метода выполнения измерений одна и та же
погрешность может проявляться как случайная или как
систематическая.
Неопределенность результата измерения характеризует тот
факт, что для данной исследуемой величины имеется
множество значений, рассеянных вокруг наилучшей оценки
результата измерения, который с различной вероятностью
могут быть приписаны измеряемой величине.

87. Общая характеристика неопределенности

Стандартная неопределенность есть неопределенность результата
измерения, характеризуемая одним стандартным отклонением.
Составляющие неопределенности могут быть разделены на два типа
(А и В) в соответствии с тем, как оценивается их численное значение.
Стандартная неопределенность типа А оценивается путем
статистического анализа результатов многократных измерений.
Стандартная неопределенность типа В оценивается с помощью
метода или подхода (включающего информацию об объекте, условиях
измерений, о применяемости эталонов и рабочих средств измерений),
которые отличаются от статистического анализа серий наблюдений и
основаны на анализе всей имеющейся информации по возможному
изменению измеряемой величины.
Суммарная (комбинированная) стандартная неопределенность
получается из стандартных неопределенностей нескольких величин
или параметров, от которых зависят измеряемые величины. Она равна
положительному квадратному корню из суммы членов, которые
являются дисперсиями или ковариациями исходных величин с
весовыми коэффициентами (коэффициентами влияния),
характеризующими отклонение результата измерений при изменении
этих величин.

88.

Расширенная, или полная, неопределенность характеризует
интервал вокруг результата измерений, в пределах которого, как можно
ожидать, находится большая часть значений, которые с достаточным
основанием можно приписать измеряемой величине (интервал
неопределенности).

89. Сравнение подходов