Chislo-e-i-pokazatelnaya-funkciya

1.

Число e и
показательна
я функция
Роль, значение и практическое применение в науке, технике и жизни

2.

Что такое число e?
Число e — это математическая константа, основание натурального логарифма, приблизительно равное 2,71828. Это
иррациональное и трансцендентное число, впервые систематически вычисленное Якобом Бернулли при изучении процессов
непрерывного роста и сложных процентов.
Часто называют числом Эйлера или числом Непера в честь математиков, внёсших вклад в его изучение.

3.

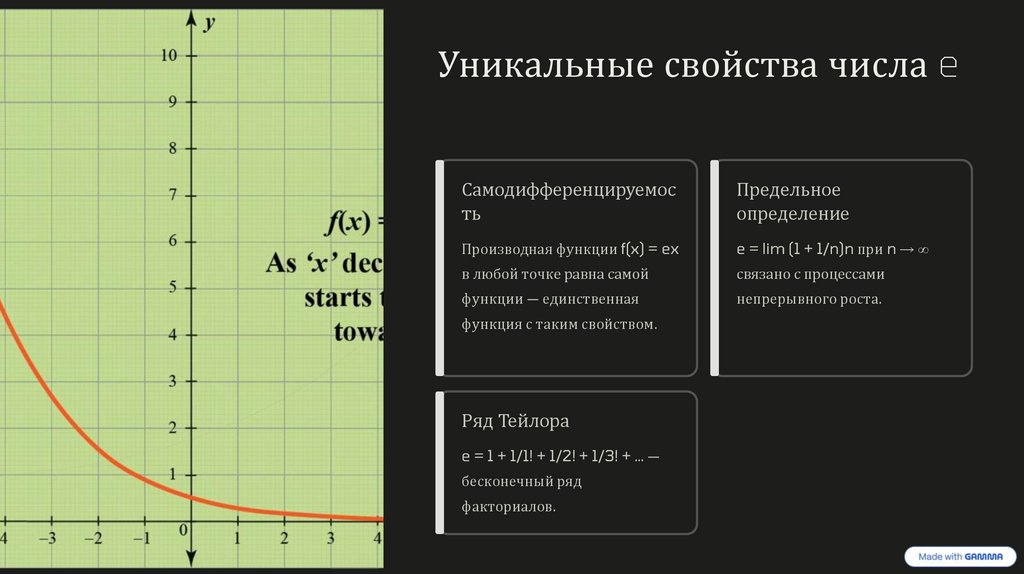
Уникальные свойства числа e
Самодифференцируемос
ть
Предельное
определение
Производная функции f(x) = ex
e = lim (1 + 1/n)n при n → ∞
в любой точке равна самой
связано с процессами
функции — единственная
непрерывного роста.
функция с таким свойством.
Ряд Тейлора
e = 1 + 1/1! + 1/2! + 1/3! + … —
бесконечный ряд
факториалов.

4.

Историческая предпосылка:
Якоб Бернулли
Якоб Бернулли поставил задачу: как растёт капитал при непрерывной
капитализации процентов?
Он обнаружил, что при всё более частом начислении процентов сумма
стремится к фиксированному значению, которое позже обозначили
буквой e.
Пример: 1000 рублей под 100% годовых с непрерывной
капитализацией превращаются в 2718 рублей — точно 1000 ×
e!

5.

Показательная функция в математике
Функция y = ex является фундаментальной в математическом анализе и описывает экспоненциальный рост и затухание.
Ключевые приложения
Дифференциальные уравнения
Теория вероятностей
Статистический анализ
Обратная функция: ln(x)

6.

Естественные науки и
техника
Радиоактивный распад
Популяции и эпидемии
Количество ядер уменьшается
Рост численности живых
по закону N(t) = N₀e−λt, где λ —
организмов и распространение
постоянная распада.
инфекций описывается
моделями с ex.
Электротехника
Заряд и разряд конденсаторов в цепях RC подчиняются
экспоненциальным законам.

7.

Экономика и финансы
Показательная функция лежит в основе современной финансовой математики и оценки инвестиций.
Формула непрерывного начисления процентов:
где P — основная сумма, r — ставка процента, t — время в годах.
Эта формула используется банками, инвестиционными фондами и при оценке финансовых рисков для более точного
моделирования реальных процессов.

8.

Тождество Эйлера — шедевр
математики
Это уравнение связывает пять фундаментальных математических
констант: e, π, мнимую единицу i, единицу 1 и ноль 0.
Считается одним из самых красивых и глубоких уравнений в математике,
показывая единство между алгеброй, геометрией и математическим
анализом.

9.

Число e в повседневной жизни
Обработка сигналов
Алгоритмы фильтрации изображений, аудиокодирования и цифровой
обработки сигналов широко используют экспоненциальные функции.
Биология и медицина
Моделирование роста клеток, скорости ферментативных реакций и
фармакокинетики лекарств основано на показательных функциях.
Машинное обучение
Алгоритмы нейронных сетей, статистические модели и системы
обработки данных используют экспоненциальное распределение.

10.

Число e — фундамент прогресса
Число e и показательная функция — это не просто математические абстракции, а универсальный язык, на котором написаны
законы природы и технологии.
Почему это важно
Ключ к пониманию всех непрерывных процессов
Инструмент для моделирования реальности
Основа современной науки и техники
Путь к новым открытиям