Similar presentations:
История пределов. Первый и второй замечательные пределы
1.
История пределов. Первый ивторой замечательные
пределы
2.
Теория пределовИнтуитивно понятие о предельном
переходе при вычислении
площадей и объемов различных
геометрических тел использовалось еще
учеными Древней Греции, особенно в
работах древнегреческого математика,
физика и инженера Архимеда (287 до
н.э. – 212 до н.э.).
3.
На интуитивном уровнепределы использовали:
второй половине 17 века английский
физик, математик и астроном Исаак
Ньютон (1642 – 1727)
4.
математики 18 века - швейцарский,немецкий и русский математик
Леонард Эйлер (1707 - 1783) и
французский математик, астроном и механик
Жозеф Луи Лагранж (1736 - 1813).
5.
Впервые определение понятияпредела было введено в работе
Дж. Валлиса «Арифметика
бесконечных величин» (XVII век),
однако исторически это понятие не
лежало в основе дифференциального и
интегрального
исчислений.
6.
Первые строгиеопределения предела
последовательности дали:
В 1816 году чешский математик, философ,
теолог Бернард Больцано (1781 - 1848) и
французский математик Огустен Луи Коши
(1789 - 1857) в 1821 году для строгого
обоснования математического анализа.
7.
Дальнейшей разработкойтеории пределов
занимались
Бернард Больцано и Карл Вейерштрасс
8.
Замеча́тельные преде́лы -термин, использующийся в советских
и российских учебниках по
математическому анализу для обозначения
некоторых широко известных
математических тождеств со взятием
предела. Замечательны они потому, что
они уже доказаны великими математиками
и нам остается лишь пользоваться ими для
удобства нахождения пределов.
9.
Замечательных пределовсуществует несколько, но самыми
известными являются первый и
второй замечательные пределы. Их
замечательность состоит в том, что
они имеют широкое применение и с
их помощью можно найти и другие
пределы, встречающиеся в
многочисленных задачах.
10.
Первый замечательныйпредел:
11.
Огустен Луи Коши(1789 - 1857)
Вывел и опубликовал
доказательства предела
функции
12.
Второй замечательныйпредел
13.
Якоб Бернули (1655-1705)В 1690 году Бернулли впервые
опубликовал исследование сложного
процента, в котором обосновал
существование предельной выгоды,
которую оценил как большую 2,5 но
меньшую 3. Путём нескольких
приближений он фактически искал предел
последовательности
который равен числу е.
14.
Решения задачи о предельнойвеличине процентного дохода
Если исходная сумма $1 и начисляется
100% годовых один раз в конце года, то
итоговая сумма будет $2. Но если те же самые
проценты начислять два раза в год, то $1
умножается на 1,5 дважды, получая
$1,00·1,52=$2,25. Начисления процентов раз в
квартал приводит к $1,00·1,254=$2,44140625, и так
далее. Бернулли показал, что если частоту
начисления процентов бесконечно увеличивать, то
процентный доход в случае сложного
процента имеет предел:
и этот предел равен числу e≈ (2,71828).









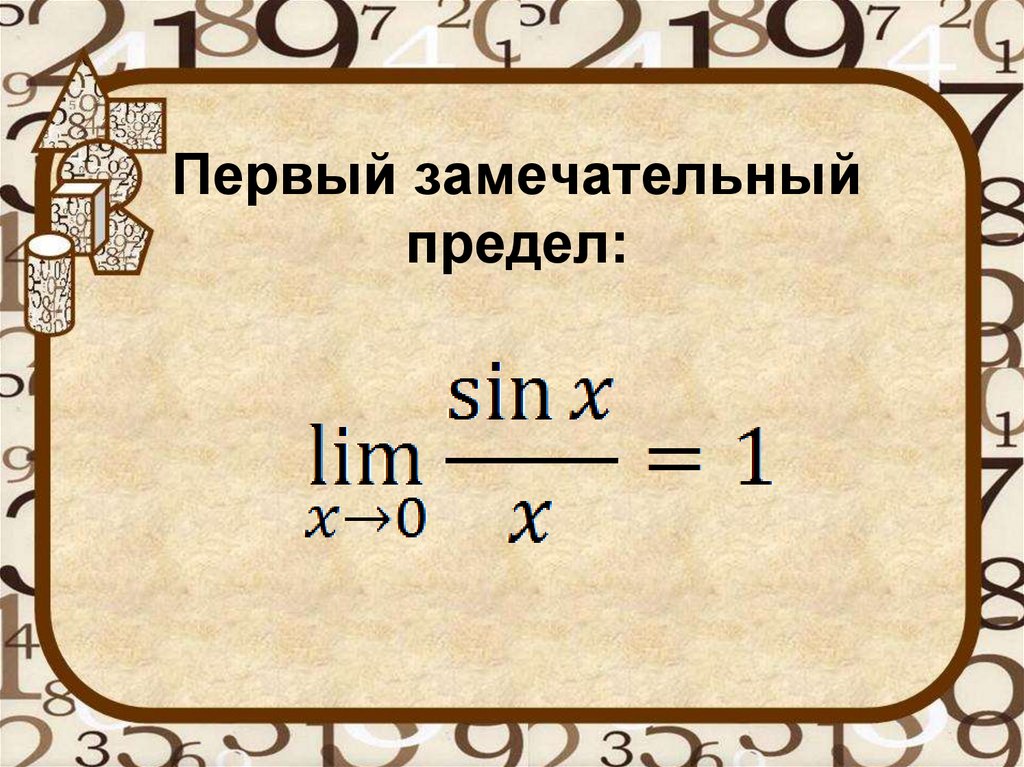




 mathematics
mathematics








