Материалы для лабораторной работы №2

1. Лабораторная работа №2 Изучение особенностей построения архитектуры многослойного персептрона в контексте задачи классификации

Автор: ассистент Отырба Р. Р.
Факультета компьютерных наук
Кафедры технологий обработки и защиты
информации

2. ЦЕЛЬ ЛАБОРАТОРНОЙ РАБОТЫ

Целью данной лабораторной работы является изучение
особенностей построения архитектуры многослойного персептрона
(MLP) для решения задач классификации с использованием
библиотеки TensorFlow. В ходе выполнения работы мы научимся
создавать и обучать нейронные сети для решения реальных задач
классификации, анализировать результаты и корректировать
архитектуру модели для достижения оптимальной точности.
2

3. СОДЕРЖАНИЕ

01
ВВОДНАЯ ТЕРМИНОЛОГИЯ
02
ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)
03
ВЫХОДНЫЕ ФУНКЦИИ АКТИВАЦИИ
04
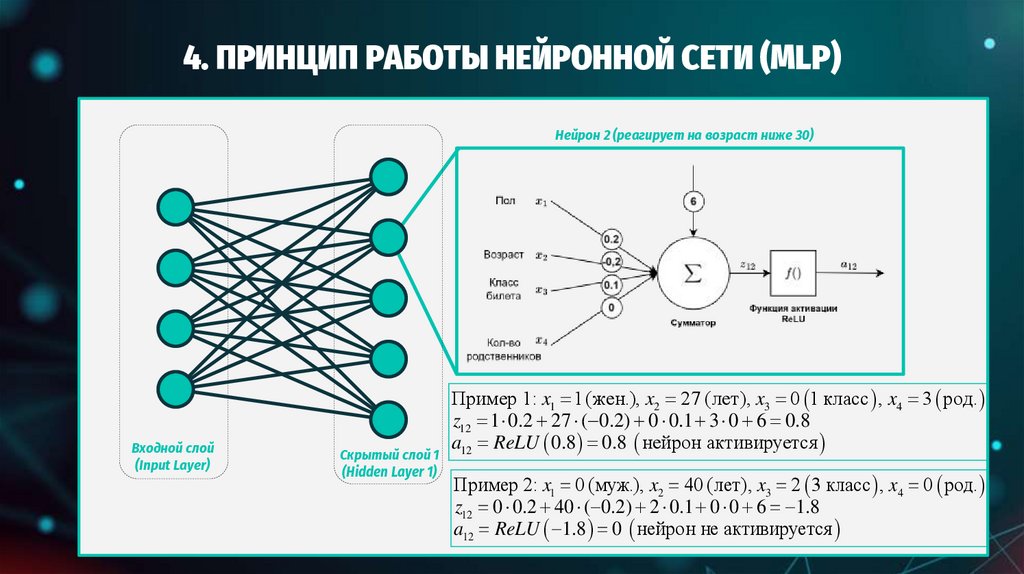
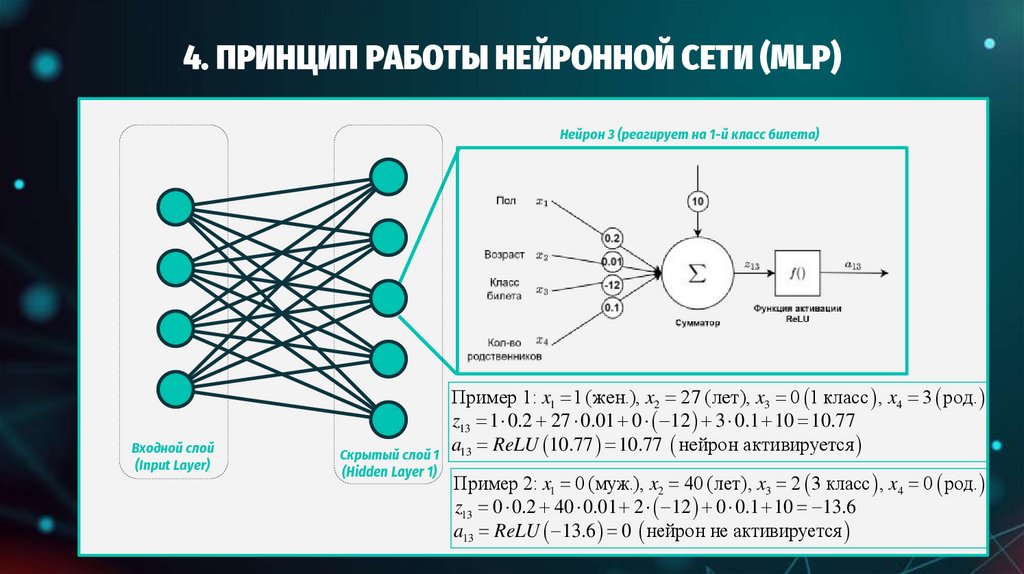
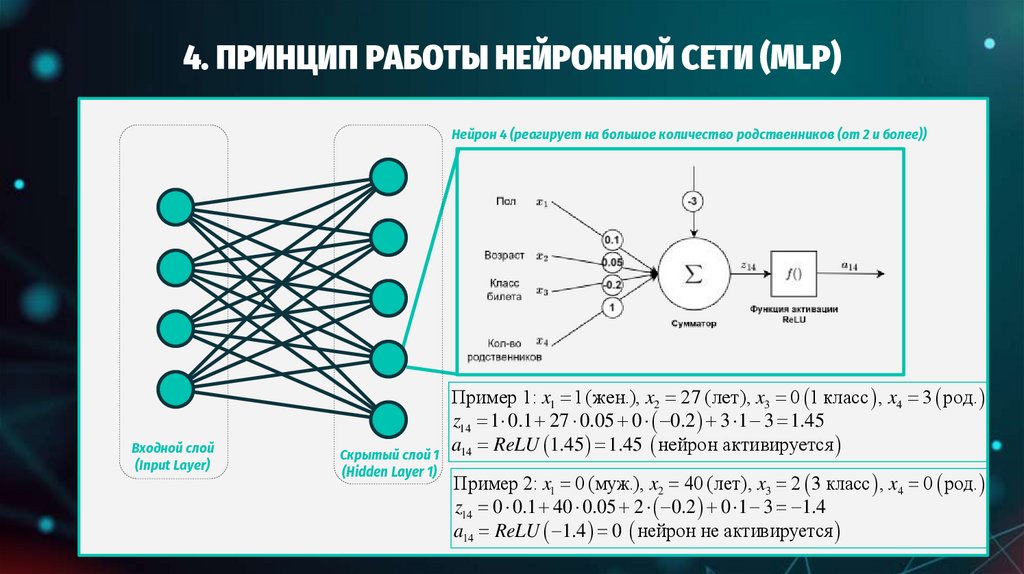
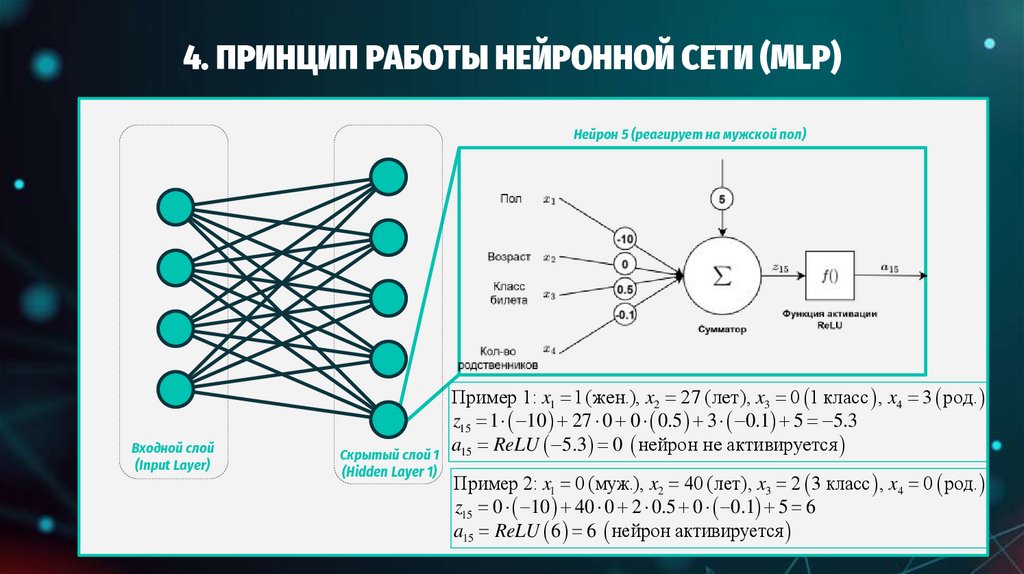
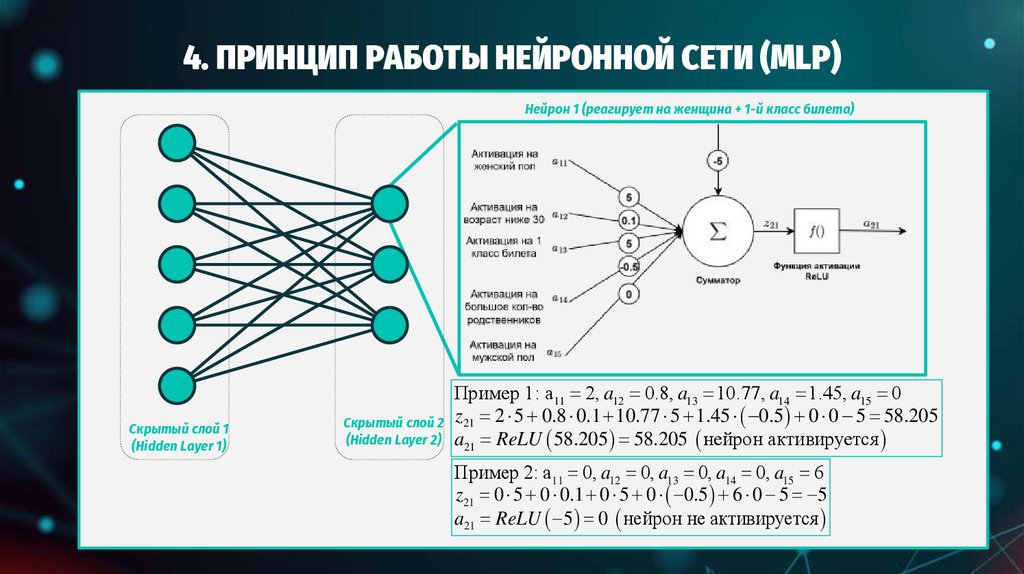
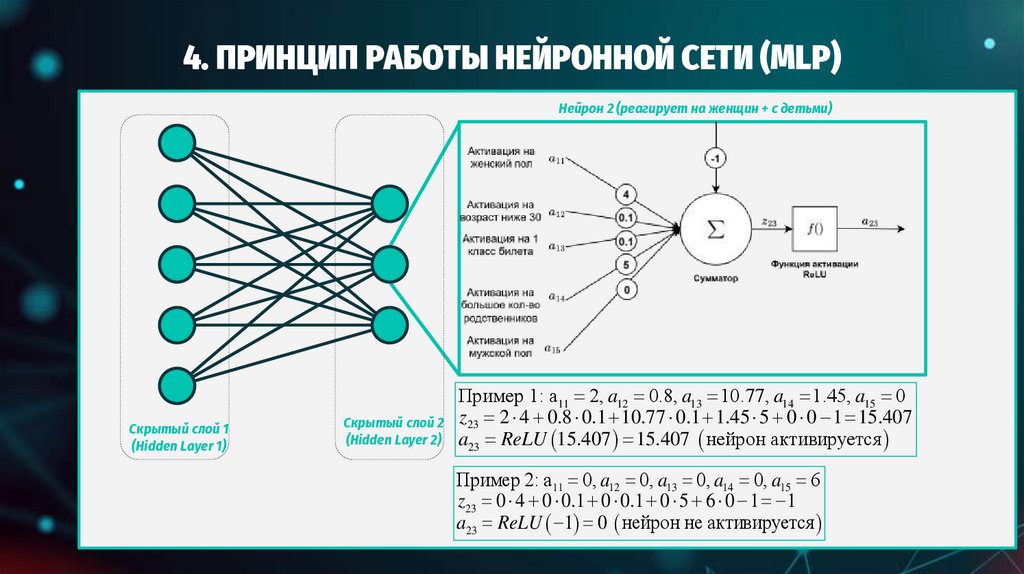
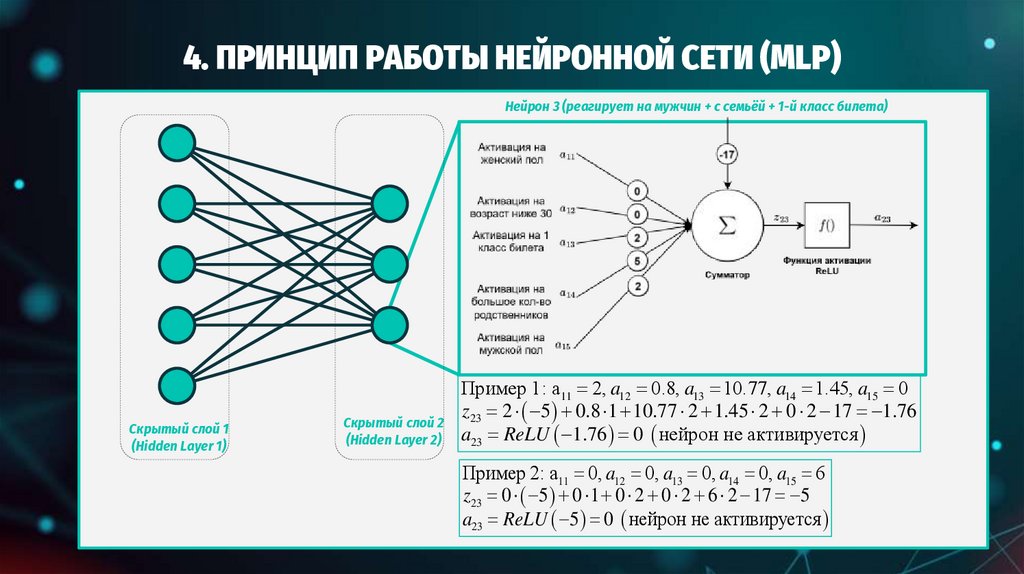
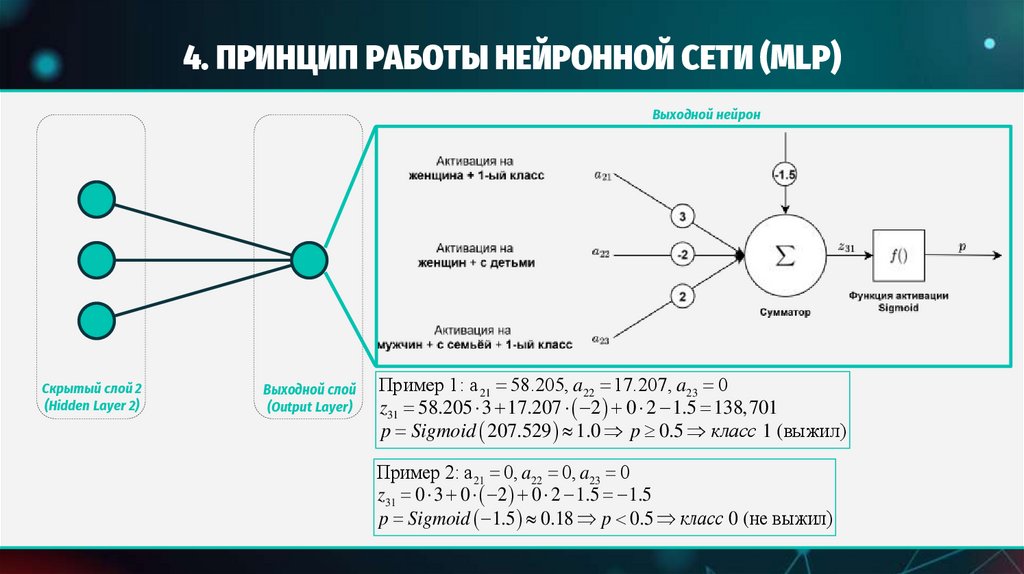
ПРИНЦИП РАБОТЫ НЕЙРОННОЙ СЕТИ (MLP)
05
МЕТРИКИ ДЛЯ ЗАДАЧИ КЛАССИФИКАЦИИ
3

4. 1. ВВОДНАЯ ТЕРМИНОЛОГИЯ

4

5. 1. ВВОДНАЯ ТЕРМИНОЛОГИЯ

Обучающий набор (Training Set):
• Это как учебник, который вы используете для изучения материала перед экзаменом. В обучающем наборе у вас есть
много примеров задач и ответов к ним. Например, задачи и правильные ответы на математические уравнения.
• В контексте обучения нейронной сети, это данные, которые мы используем для "обучения" модели. Нейронная сеть
анализирует эти примеры и пытается "выучить" правильные ответы.
Валидационный набор (Validation Set):
• Это как небольшой проверочный тест, который вы выполняете после изучения материала, чтобы убедиться, что вы
усвоили его правильно. В нем также есть задачи и ответы, но вы не использовали их в процессе обучения. Если ваши
ответы на проверочном тесте сходятся с правильными ответами, это означает, что вы успешно усвоили материал.
• В контексте нейронных сетей, валидационный набор используется для оценки производительности модели в процессе
обучения после каждой эпохи обучения. Мы не тренируем модель на этих данных, но проверяем, насколько хорошо она
обобщает знания из обучающего набора на новые данные.
Тестовый набор (Test Set):
• Это как сам экзамен, который вы сдаете в конце подготовки. В нем также есть задачи и ответы, и вы не видели их ни в
учебнике, ни на проверочных тестах. Этот тест позволяет определить, насколько хорошо вы понимаете материал, не
подглядывая в учебник или на проверочные тесты.
• В контексте нейронных сетей, тестовый набор используется для окончательной оценки производительности модели.
Это своего рода последний экзамен, чтобы убедиться, что модель действительно научилась решать задачу и готова к
реальному использованию.
5

6. 1. ВВОДНАЯ ТЕРМИНОЛОГИЯ

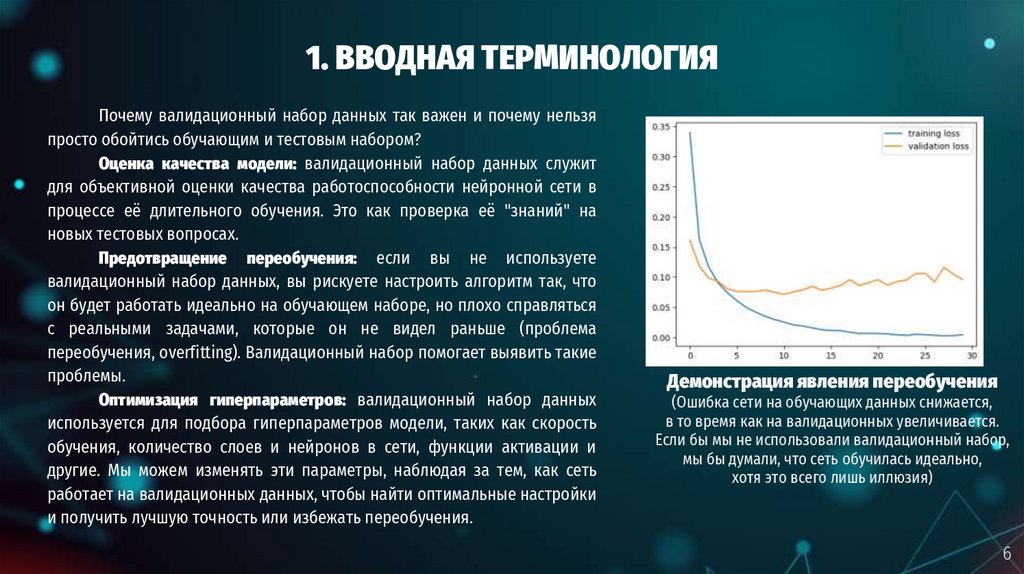
Почему валидационный набор данных так важен и почему нельзя
просто обойтись обучающим и тестовым набором?
Оценка качества модели: валидационный набор данных служит
для объективной оценки качества работоспособности нейронной сети в
процессе её длительного обучения. Это как проверка её "знаний" на
новых тестовых вопросах.
Предотвращение переобучения: если вы не используете
валидационный набор данных, вы рискуете настроить алгоритм так, что
он будет работать идеально на обучающем наборе, но плохо справляться
с реальными задачами, которые он не видел раньше (проблема
переобучения, overfitting). Валидационный набор помогает выявить такие
проблемы.
Оптимизация гиперпараметров: валидационный набор данных
используется для подбора гиперпараметров модели, таких как скорость
обучения, количество слоев и нейронов в сети, функции активации и
другие. Мы можем изменять эти параметры, наблюдая за тем, как сеть
работает на валидационных данных, чтобы найти оптимальные настройки
и получить лучшую точность или избежать переобучения.
Демонстрация явления переобучения
(Ошибка сети на обучающих данных снижается,
в то время как на валидационных увеличивается.
Если бы мы не использовали валидационный набор,
мы бы думали, что сеть обучилась идеально,
хотя это всего лишь иллюзия)
6

7. 1. ВВОДНАЯ ТЕРМИНОЛОГИЯ

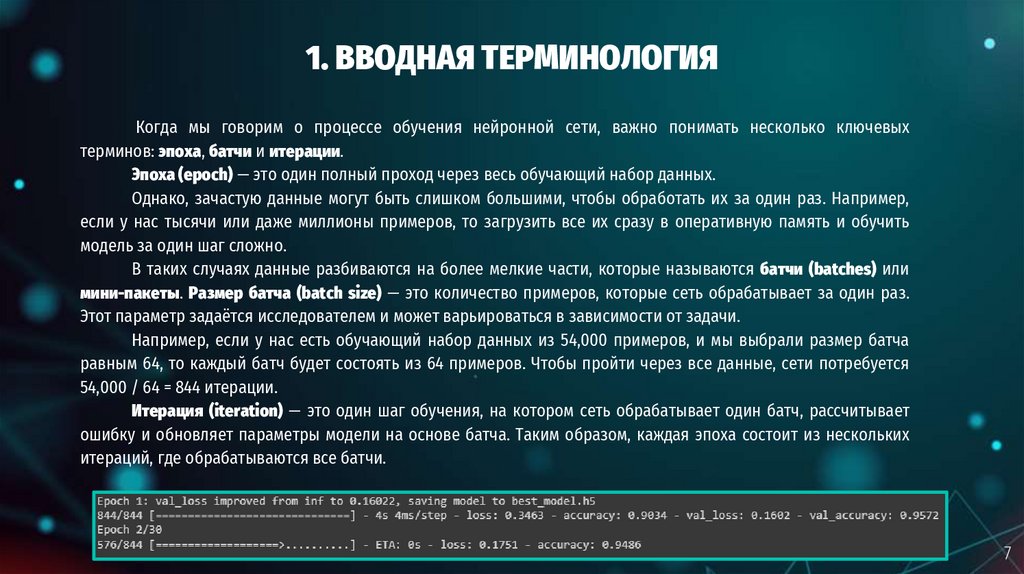
Когда мы говорим о процессе обучения нейронной сети, важно понимать несколько ключевых
терминов: эпоха, батчи и итерации.
Эпоха (epoch) — это один полный проход через весь обучающий набор данных.
Однако, зачастую данные могут быть слишком большими, чтобы обработать их за один раз. Например,
если у нас тысячи или даже миллионы примеров, то загрузить все их сразу в оперативную память и обучить
модель за один шаг сложно.
В таких случаях данные разбиваются на более мелкие части, которые называются батчи (batches) или
мини-пакеты. Размер батча (batch size) — это количество примеров, которые сеть обрабатывает за один раз.
Этот параметр задаётся исследователем и может варьироваться в зависимости от задачи.
Например, если у нас есть обучающий набор данных из 54,000 примеров, и мы выбрали размер батча
равным 64, то каждый батч будет состоять из 64 примеров. Чтобы пройти через все данные, сети потребуется
54,000 / 64 = 844 итерации.
Итерация (iteration) — это один шаг обучения, на котором сеть обрабатывает один батч, рассчитывает
ошибку и обновляет параметры модели на основе батча. Таким образом, каждая эпоха состоит из нескольких
итераций, где обрабатываются все батчи.
7

8. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

8

9. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

Прежде чем приступить к решению такой задачи
необходимо понять принцип построения архитектуры нейронной
сети. Для этого, сперва, необходимо закрепить терминологию,
позволяющую нам указывать на разные части сети.
1.
Входной слой — это первый слой нейронной сети, который
предназначен для приема входных данных. Количество
нейронов в этом слое соответствует количеству
(размерности) признаков X входных данных.
2.
Скрытые слои — это внутренние слои, которые
располагаются между входным и выходным слоями сети. Эти
слои выполняют основные вычисления. С их помощью
нейронная сеть учится находить важные связи и
закономерности в данных.
Выбор правильного количества скрытых слоёв и количества
нейронов в каждом слое является очень важным этапом.
Слишком
малое
количество
может
привести
к
недообучению, а слишком большое повлечет за собой
увеличение времени обучения сети или к переобучению.
Полностью связанная нейронная сеть
(Feed-Forward Network (FFN))
или
Многослойный персептрон
(Multilayer Perceptron (MLP))

10. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

3.
Выходной слой отвечает за то, чтобы на основе
обработанных данных выдать результат — предсказание
или классификацию. Количество нейронов в этом слое
зависит от типа задачи:
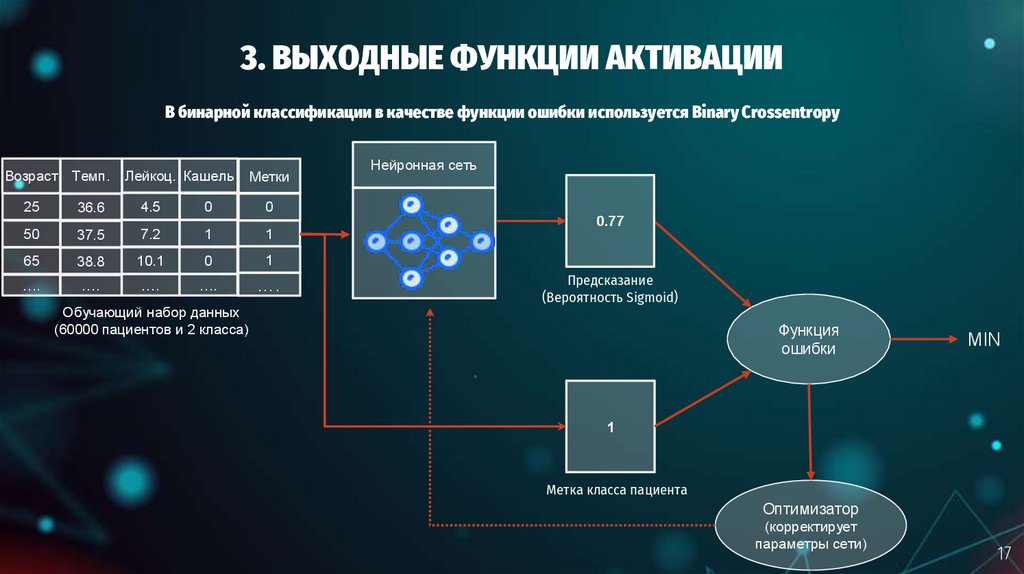
Для бинарной классификации используется 1 нейрон с
функцией активации sigmoid. Этот нейрон выдаёт
значение,
интерпретируемое
как
вероятность
принадлежности к положительному классу.
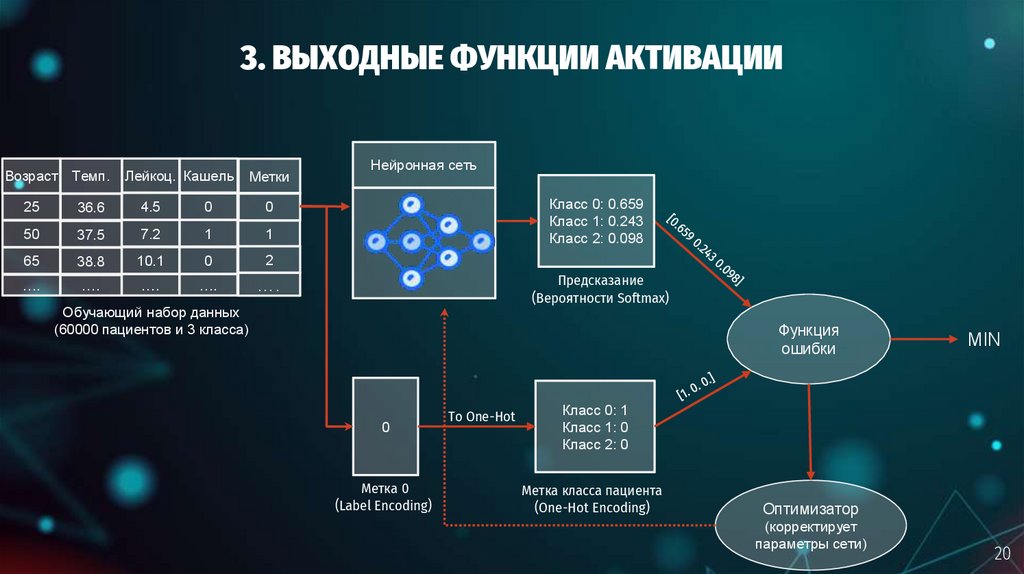
Для многоклассовой классификации количество
нейронов в выходном слое соответствует числу классов.
Для каждого класса сеть выдаёт вероятность с помощью
функции активации softmax, которая нормализует
предсказания так, чтобы их сумма была равна 1.
Для регрессионных задач выходной слой может иметь
один или несколько нейронов, в зависимости от того,
сколько целевых переменных нужно предсказать. Здесь
чаще всего не используются функции активации, так как
нам нужны сырые числовые значения, а не вероятности.
Полностью связанная нейронная сеть
(Feed-Forward Network (FFN))
или
Многослойный персептрон
(Multilayer Perceptron (MLP))

11. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

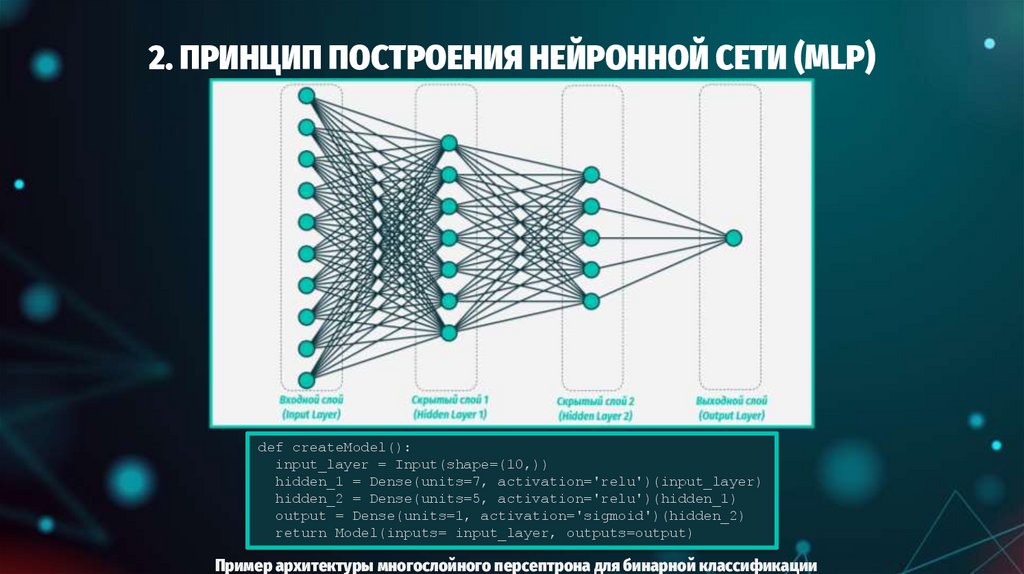
def createModel():
input_layer = Input(shape=(10,))
hidden_1 = Dense(units=7, activation='relu')(input_layer)
hidden_2 = Dense(units=5, activation='relu')(hidden_1)
output = Dense(units=1, activation='sigmoid')(hidden_2)
return Model(inputs= input_layer, outputs=output)
Пример архитектуры многослойного персептрона для бинарной классификации

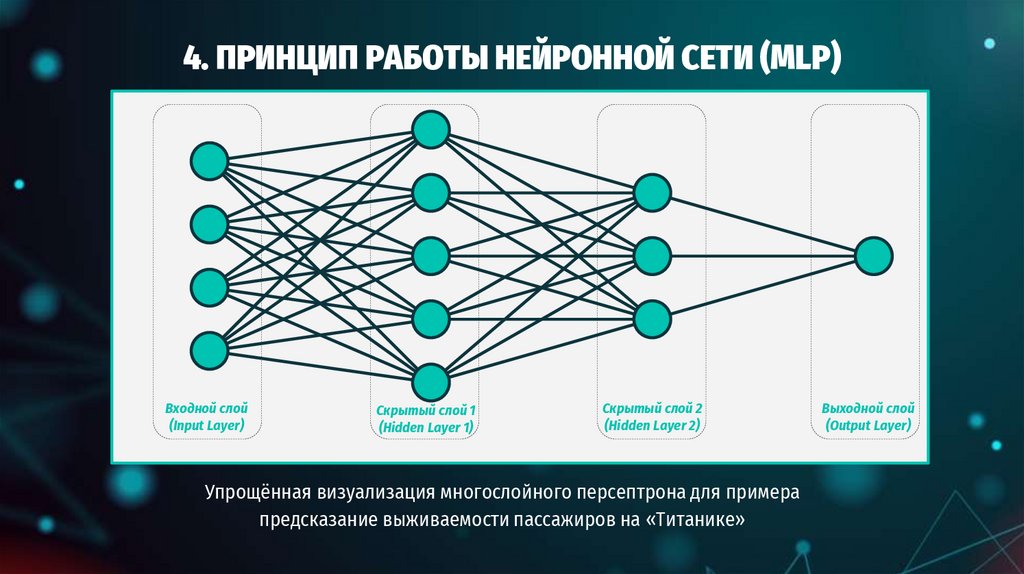
12. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

Входной слой
(Input Layer)
Скрытый слой 1
(Hidden Layer 1)
Скрытый слой 2
(Hidden Layer 2)
Выходной слой
(Output Layer)
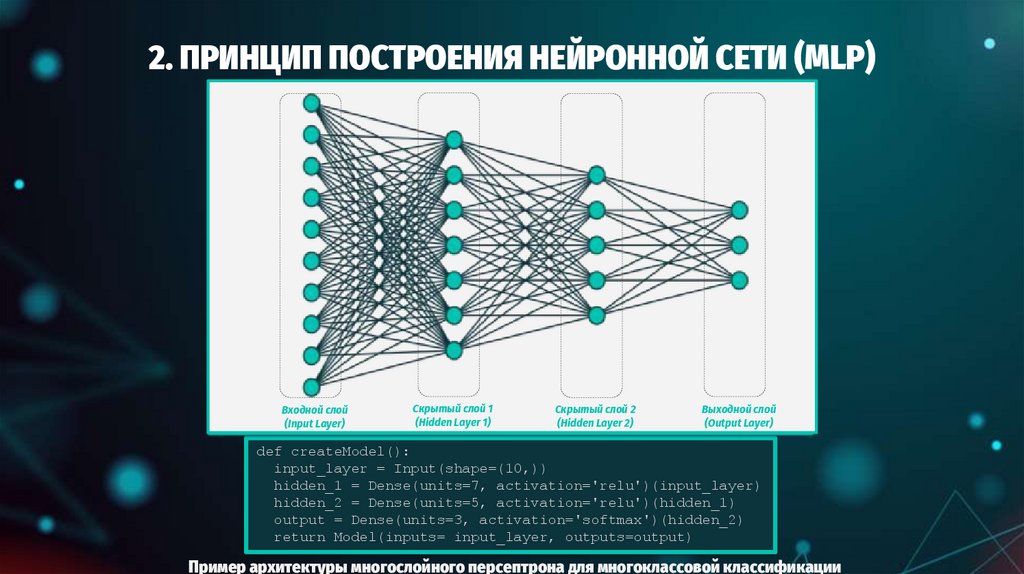
def createModel():
input_layer = Input(shape=(10,))
hidden_1 = Dense(units=7, activation='relu')(input_layer)
hidden_2 = Dense(units=5, activation='relu')(hidden_1)
output = Dense(units=3, activation='softmax')(hidden_2)
return Model(inputs= input_layer, outputs=output)
Пример архитектуры многослойного персептрона для многоклассовой классификации

13. 2. ПРИНЦИП ПОСТРОЕНИЯ НЕЙРОННОЙ СЕТИ (MLP)

Существуют эвристические правила выбора количества нейронов в скрытых слоях. Одним из таких правил
является правило геометрической пирамиды (Geometric pyramid rule). Это правило рекомендует постепенно
уменьшать количество нейронов по мере продвижения от входного к выходному слою. Для нейронной сети с ℎ
скрытыми слоями количество нейронов в каждом слое вычисляется следующим образом:
m
ki n
n
i
h 1
где k – число нейронов в скрытом слое, n – число нейронов в входном слое, m – число нейронов в выходном слое,
h – количество скрытых слоёв, i – номер скрытого слоя (нумерация от 1 до ℎ).
Для одного слоя: k nm
Однако на практике количество как слоев, так и нейронов часто подбираются эмпирически, то есть
экспериментальным путём. Начинают обычно с более простой сети — с одного скрытого слоя, постепенно
усложняя архитектуру по мере необходимости. Этот процесс называется Network Growing (увеличение сложности
сети).
Также для автоматизации выбора параметров модели могут использоваться методы автоматического
подбора гиперпараметров, такие как Grid Search, Random Search и Bayesian Optimization. Эти методы позволяют
эффективно исследовать пространство гиперпараметров (например, количество слоев, нейронов, скорость
обучения) и найти оптимальные настройки для конкретной задачи.

14. 3. ВЫХОДНЫЕ ФУНКЦИИ АКТИВАЦИИ

14

15. 3. ВЫХОДНЫЕ ФУНКЦИИ АКТИВАЦИИ

Сигмоида (Sigmoid) используется для задач бинарной классификации (где два класса: 0 или 1). Функция
принимает выходное значение нейрона