Similar presentations:
13-14_Течії у мережах
1.
Комп'ютерна дискретна математикаТранспортні мережі
Лекція 13-14
Н.В. Білоус
Факультет комп’ютерных наук
Кафедра ПІ, ХНУРЕ
ХНУРЕ, кафедра ПІ, e-mail: bilous.nataliya@nure.ua
2. Основні визначення
Мережа - це зв'язний орієнтований граф без петель, вякому :
1. Є тільки одна вершина (вузол), в яку не входить
жодна дуга, яка називається входом (витоком) x0
2. Є тільки одна, вершина (вузол), з якої не виходить
жодна дуга, яка називається виходом (стоком) z
3. Кожній дузі u присвоєна числова характеристика
C(u) 0, яка називається пропускною здатністю дуги u
2
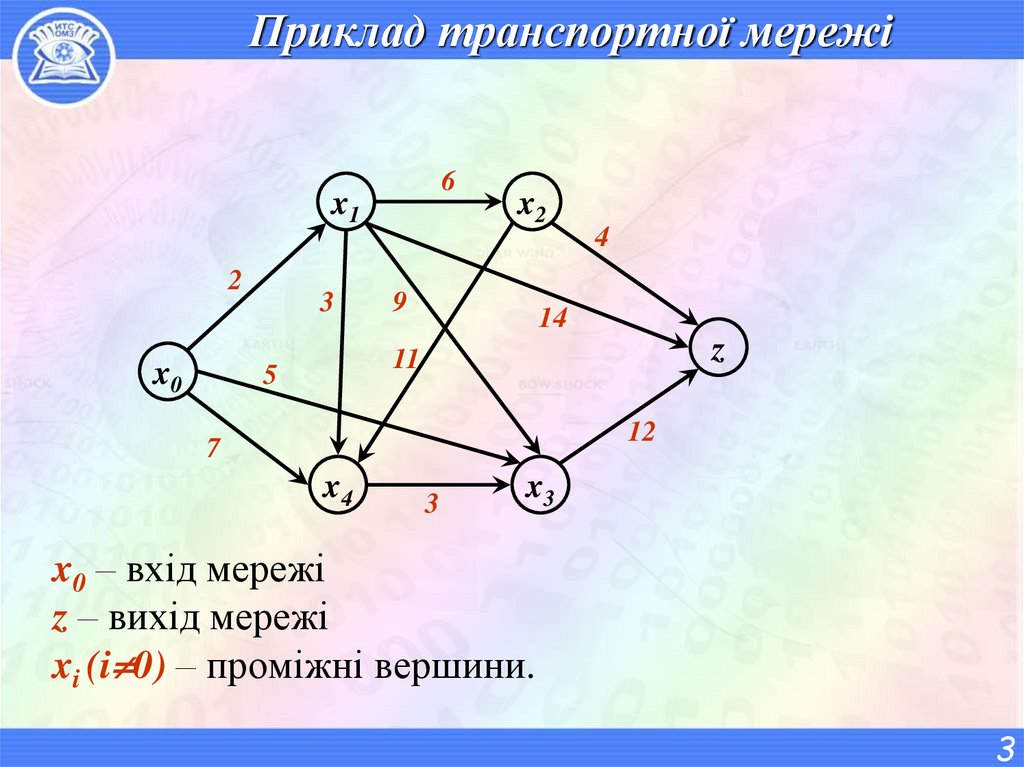
3. Приклад транспортної мережі
6x1
2
x0
3
x2
9
4
14
z
11
5
12
7
x4
3
x3
x0 – вхід мережі
z – вихід мережі
xi (i 0) – проміжні вершини.
3
4. Течії у мережах
Течією у транспортній мережі називаєтьсяфункція (u), задана на множині дуг мережі, яке
задовольняє властивостям :
0 ( u ) C( u )
1)
2)
( u ) ( u )
u U x
u U x
.
( U ) ( U )
u U x 0
u U z
z
U x множина дуг, що входять в вершину х
U x множина дуг, що виходять з вершини х
z
течія у транспортній мережі
4
5. Основні визначення
Дуга u називається насиченою, якщо потік(u)=C(u)
Дуга u називається вільною якщо (u)=0
Дуга u називається зайнятою, якщо (u)>0
Течія у мережі називається повною, якщо будьякий шлях, що йде від входу до виходу мережі
містить хоча б одну насичену дугу.
5
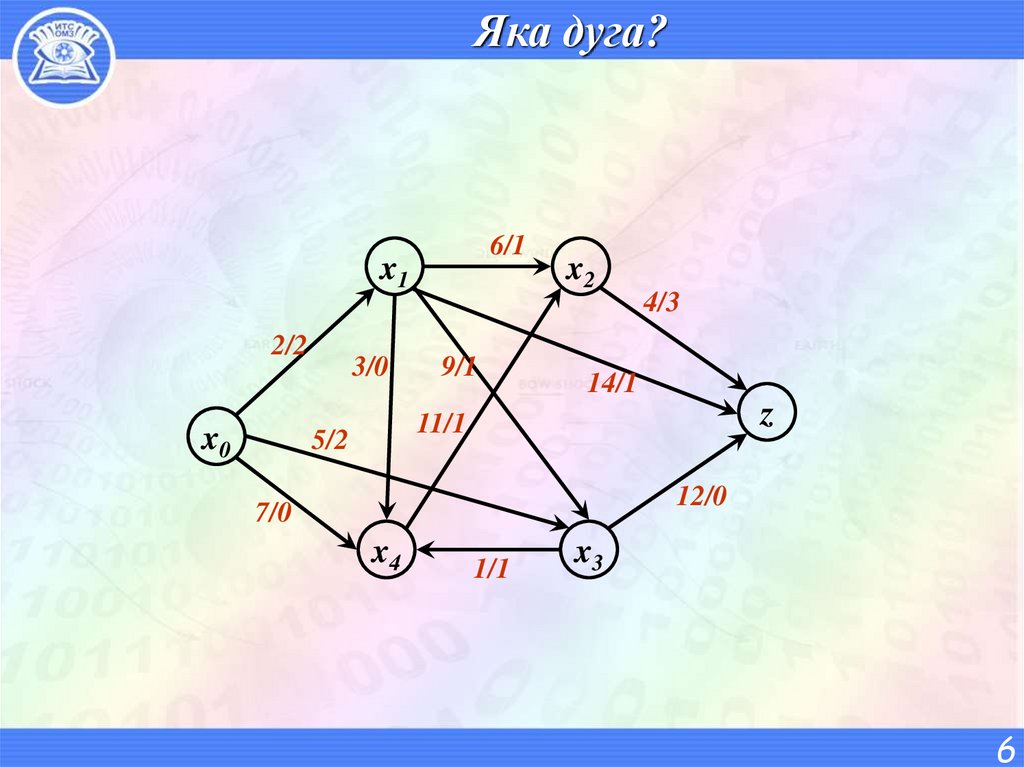
6. Яка дуга?
6/1x1
2/2
x0
3/0
9/1
x2
4/3
14/1
z
11/1
5/2
12/0
7/0
x4
1/1
x3
6
7. Розріз транспортної мережі
Розрізом називається множина дуг, що з'єднуютьвершини множини
A і A.
U A U U
A
A
( U ) ( U )
u U A
u U A
z
C( A ) C( U )
u U A
A сукупність вершин мережі така, що x0 A а z A .
A сукупність вершин мережі така, що x0 A а z A .
U A множина дуг, що входять в вершини множини А
U A множина дуг, що виходять з вершини множини А
7
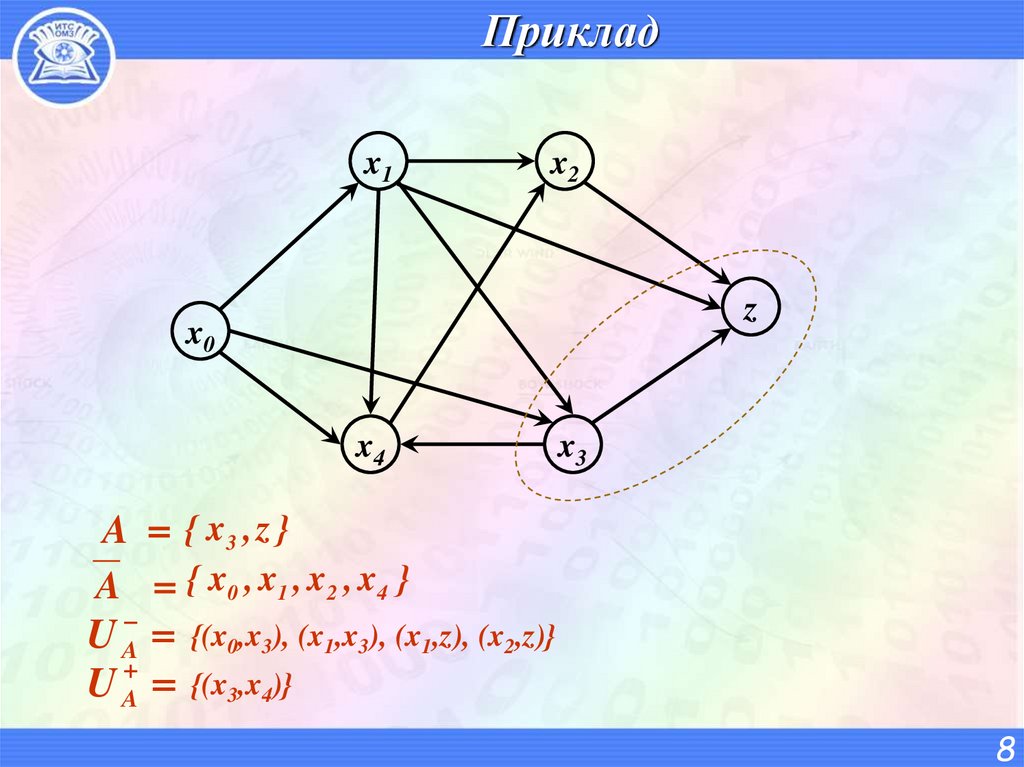
8. Приклад
x1x2
z
x0
x4
x3
A { x3 , z }
A { x0 , x 1 , x 2 , x 4 }
U A {(x0,x3), (x1,x3), (x1,z), (x2,z)}
U A {(x3,x4)}
8
9. Завдання про найбільшу течію у мережі
При заданій конфігурації і зазначених пропускнихспроможностях дуг визначити максимальну течію, яку
можна пропустити через мережу і її розподіл по дугам.
9
10. Теорема Форда-Фалкерсона
Якщо в транспортній мережі для деякогорозрізу V і величини течії z має місце C(A)= z ,
тоді V має мінімальну пропускну спроможність в
мережі, а z є максимальна для даної мережі.
10
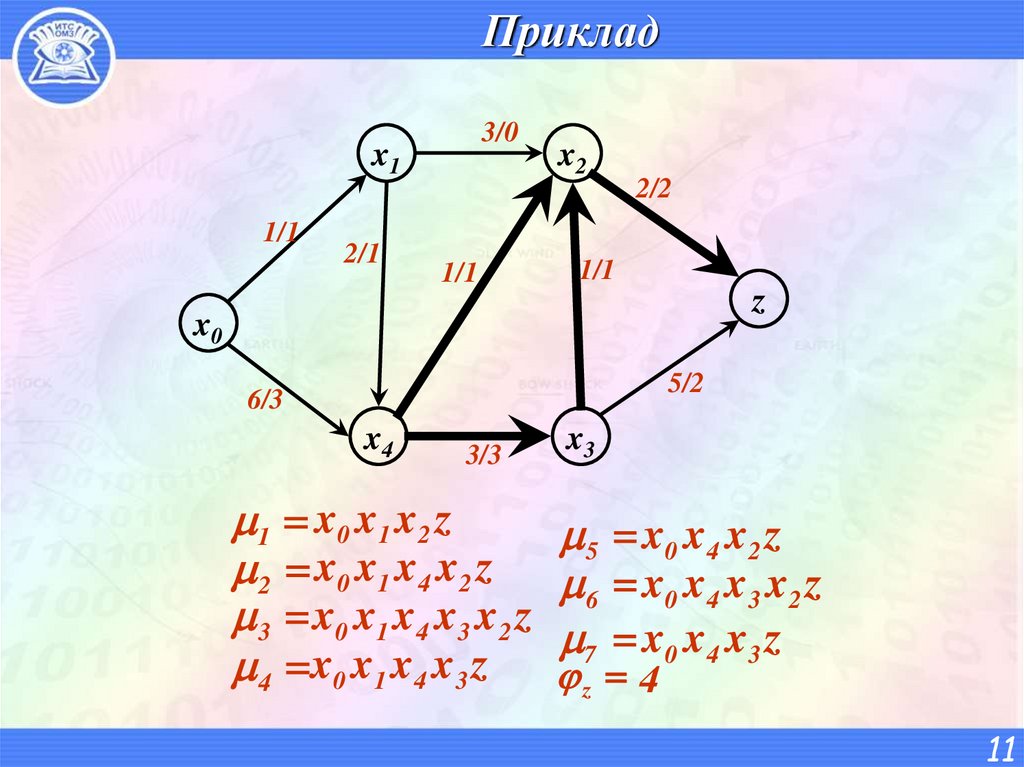
11. Приклад
3/0x1
1/1
2/1
1/1
x2
2/2
1/1
z
x0
5/2
6/3
x4
3/3
x3
1 x0 x 1 x 2 z
5 x0 x 4 x 2 z
2 x0 x 1 x 4 x 2 z x x x x z
6
0 4 3 2
3 x0 x1 x4 x3 x2 z x x x z
4 x0 x1 x4 x3 z z7 4 0 4 3
11
12. Алгоритм Форда-Фалкерсона
Алгоритм в основному включає 2 етапи:1.Знаходження повної течії.
2.Знаходження максимальної течії, за допомогою
передачи позначок.
12
13. 1. Знаходження повної течії
По черзі розглянемо всі шляхи між х0 і z і для кожноїдуги обраного шляху знайдемо різницю між пропускною
спроможністю дуги і течією, що проходить по дузі.
Збільшимо течію таким чином, щоб шлях, що веде з х0
в z містив хоча б одну насичену дугу.
Для кожної дуги обраного шляху додаємо
чисельника мінімальну отриману різницю ∆.
до
Вибираємо наступний шлях. Повторюємо ці дії до тих
пір, поки не отримаємо повну течію у мережі.
13
14. 2. Знаходження максимальної течії, за допомогою передачі позначок
Збільшення течії z у мережі полягає в розмітцівершин індексами, що вказують шлях, по якому
можлива зміна течії. Якщо розмітка досягає
вершини z, то течію можна збільшити шляхом,
відповідним отриманої розмітки. Збільшення потоку
можливо до тих пір, поки в результаті розмітки
вершина z отримує позначку.
14
15. 2. Знаходження максимальної течії, за допомогою передачі міток
Крок 1. Помічаємо вершину х0 індексом0
Крок 2. Якщо xi вже має позначку, то:
Позначка +i приписується всім непоміченим вершинам, які
пов'язані з xi ненасиченої дугою, що веде з xi до даної
вершини. Позначку отримують всі вершини y, що
задовольняють умовам :
y – непомічена
( xi , y ) U , ( xi , y ) C ( xi , y )
Позначку -i отримують всі непомічені вершини, пов'язані
зайнятою дугою, що йде з даної вершини у вершину xi .
Позначку отримують всі вершини y, що задовольняють
умовам:
у – непомічена
( y , xi ) U , ( xi , y ) 0
15
16. 2. Знаходження максимальної течії, за допомогою передачі позначок (продовження)
Крок 3. Якщо в результаті такої розмітки буде позначенавершина z, то переходимо до пункту 4. В іншому
випадку, течія, отримана на попередньому циклі,
максимальна.
Крок 4. Будуємо шлях від х0 до z, всі вершини якого
відповідають номерам позначок попередніх вершин з
точністю до знака. побудова шляху починається від
вершини z. Течія у всіх дугах шляху змінюється за
такими правилами :
якщо u
( u ),
якщо напрямок дуги u і напрямок течії у мережі
( u ) ( u ) 1 , співпадають
( u ) 1 , якщо дуга u і напрямок течії протилежні
z z 1
16
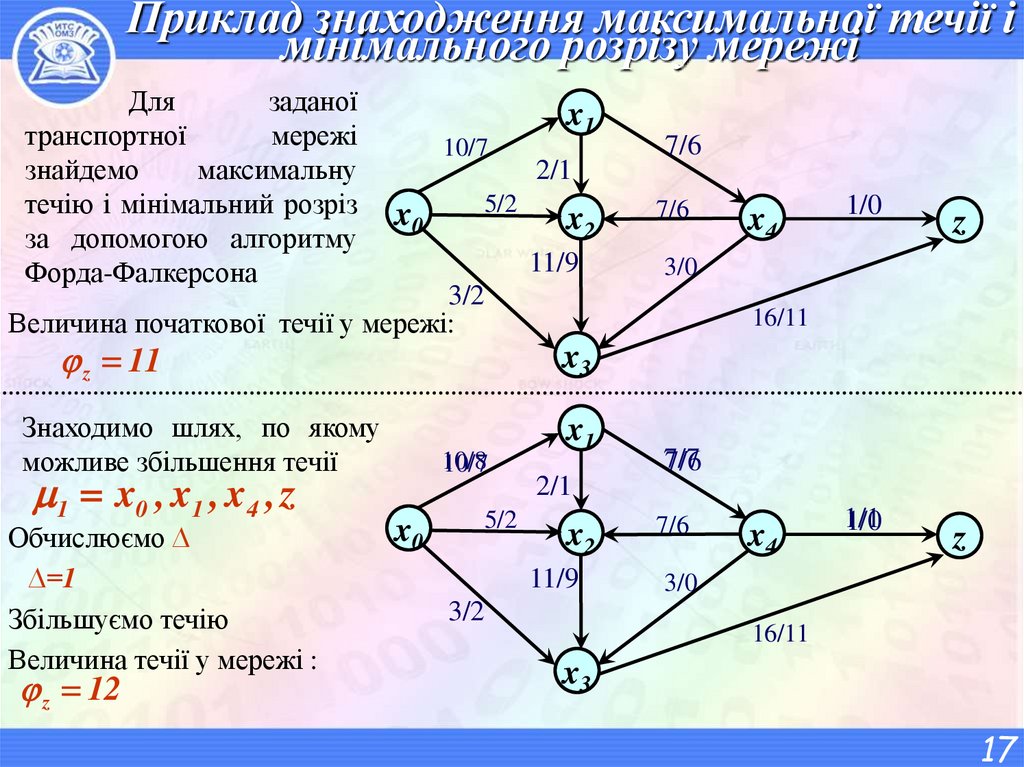
17. Приклад знаходження максимальної течії і мінімального розрізу мережі
Длязаданої
транспортної
мережі
знайдемо
максимальну
течію і мінімальний розріз
за допомогою алгоритму
Форда-Фалкерсона
x1
10/7
x0
5/2
2/1
7/6
x2
7/6
11/9
3/0
3/2
Величина початкової течії у мережі:
z 11
Обчислюємо ∆
∆=1
Збільшуємо течію
Величина течії у мережі :
z 12
1/0
z
16/11
x3
Знаходимо шлях, по якому
можливе збільшення течії
1 x0 , x1 , x4 , z
x4
10/8
10/7
x0
5/2
x1
2/1
7/7
7/6
x2
7/6
11/9
3/0
3/2
x4
1/1
1/0
z
16/11
x3
17
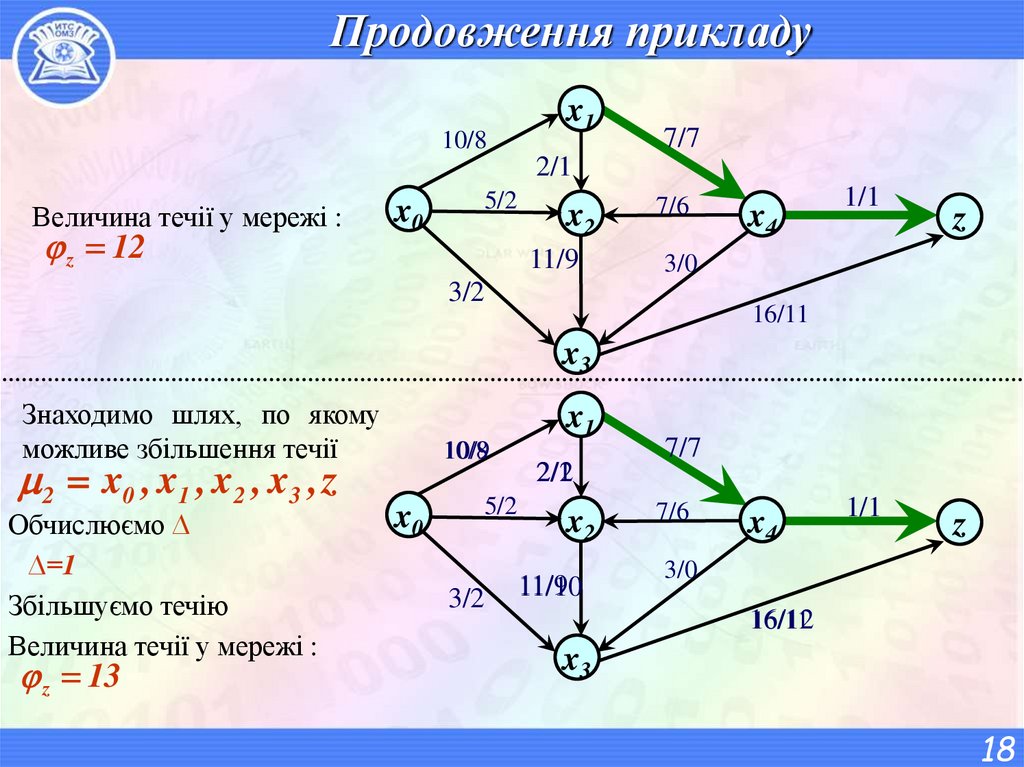
18. Продовження прикладу
10/8x1
7/7
2/1
Величина течії у мережі :
z 12
x0
5/2
x2
7/6
11/9
3/0
3/2
x4
1/1
z
16/11
x3
Знаходимо шлях, по якому
можливе збільшення течії
2 x0 , x1 , x2 , x3 , z
Обчислюємо ∆
∆=1
Збільшуємо течію
Величина течії у мережі :
z 13
x1
10/8
10/9
x0
5/2
3/2
2/1
2/2
x2
11/9
11/10
7/7
7/6
x4
1/1
z
3/0
16/11
16/12
x3
18
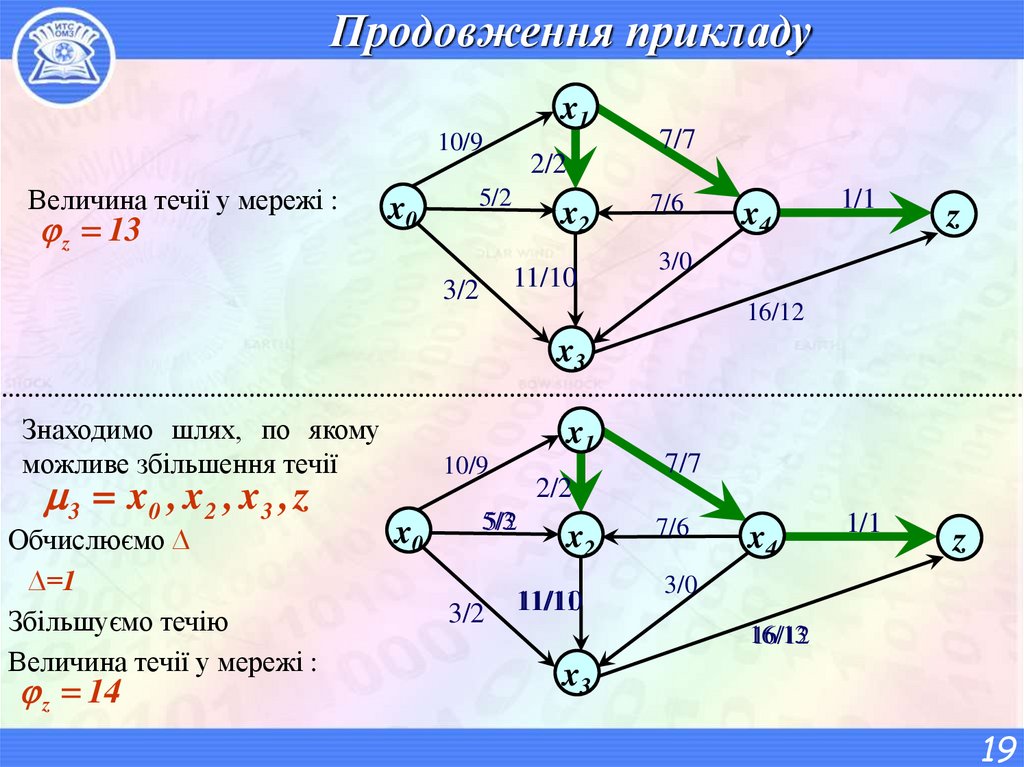
19. Продовження прикладу
x110/9
Величина течії у мережі :
z 13
x0
2/2
5/2
x2
11/10
3/2
7/7
7/6
x4
1/1
z
3/0
16/12
x3
Знаходимо шлях, по якому
можливе збільшення течії
3 x0 , x 2 , x 3 , z
Обчислюємо ∆
∆=1
Збільшуємо течію
Величина течії у мережі :
z 14
x1
10/9
x0
2/2
5/3
5/2
3/2
x2
11/11
11/10
7/7
7/6
x4
1/1
z
3/0
16/13
16/12
x3
19
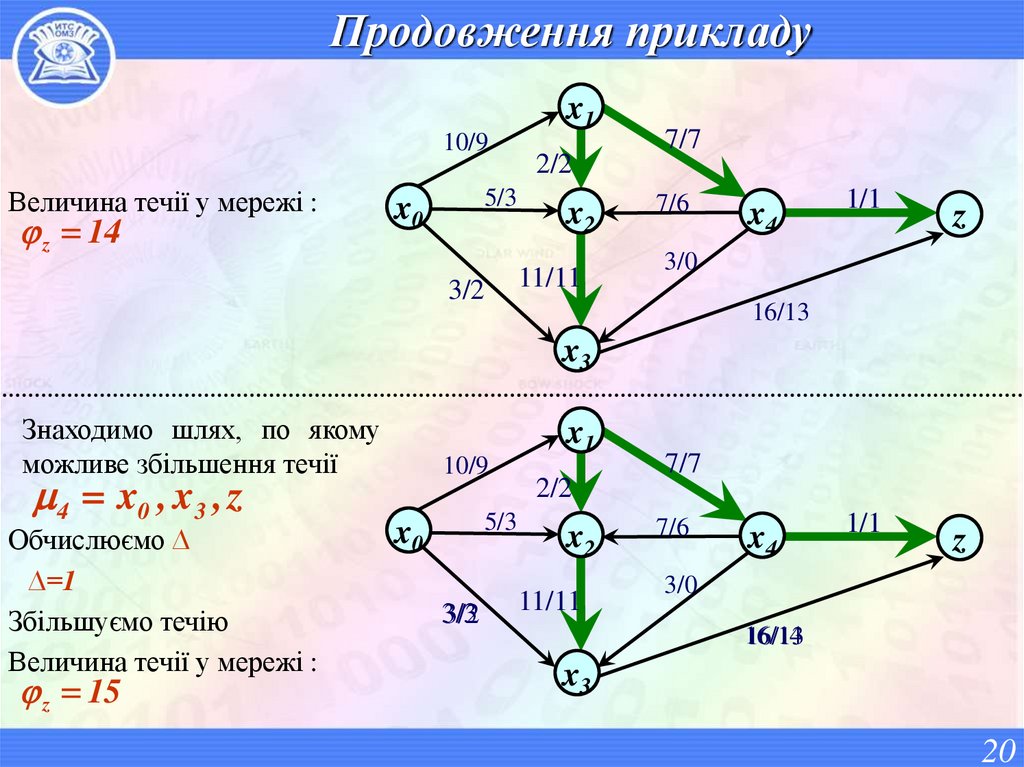
20. Продовження прикладу
x110/9
Величина течії у мережі :
z 14
5/3
x0
3/2
2/2
x2
11/11
7/7
7/6
x4
1/1
z
3/0
16/13
x3
Знаходимо шлях, по якому
можливе збільшення течії
4 x0 , x3 , z
Обчислюємо ∆
∆=1
Збільшуємо течію
Величина течії у мережі :
z 15
x1
10/9
5/3
x0
3/3
3/2
2/2
x2
11/11
7/7
7/6
x4
1/1
z
3/0
16/14
16/13
x3
20
21. Продовження прикладу
x110/9
7/7
2/2
0
x0
+0
5/3
5/4
+0
x2
11/11
-2
7/6
7/5
x4
1/1
+3
z
3/0
3/1
3/3
+4
16/14
16/15
x3
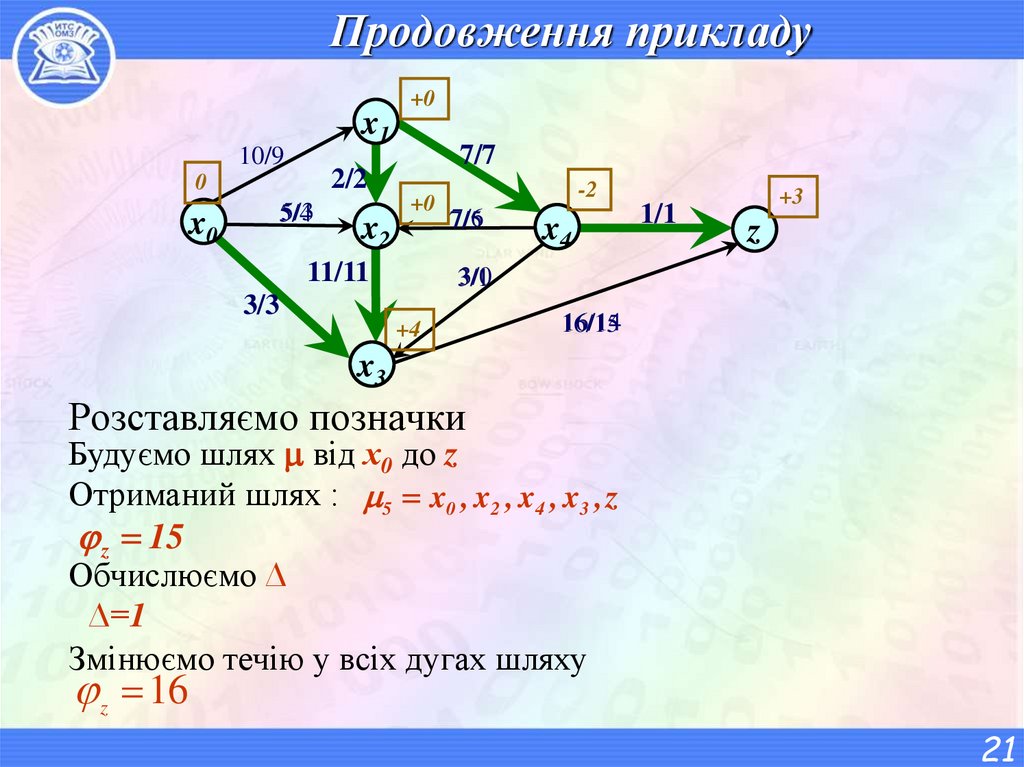
Розставляємо позначки
Будуємо шлях від х0 до z
Отриманий шлях : 5 x0 , x2 , x4 , x3 , z
z 15
Обчислюємо ∆
∆=1
Змінюємо течію у всіх дугах шляху
z 16
21
22. Продовження прикладу
x110/9
7/7
2/2
0
5/5
5/4
x0
+0
+0
x2
11/11
-2
7/4
7/5
x4
1/1
+3
z
3/2
3/1
3/3
+4
16/16
16/15
x3
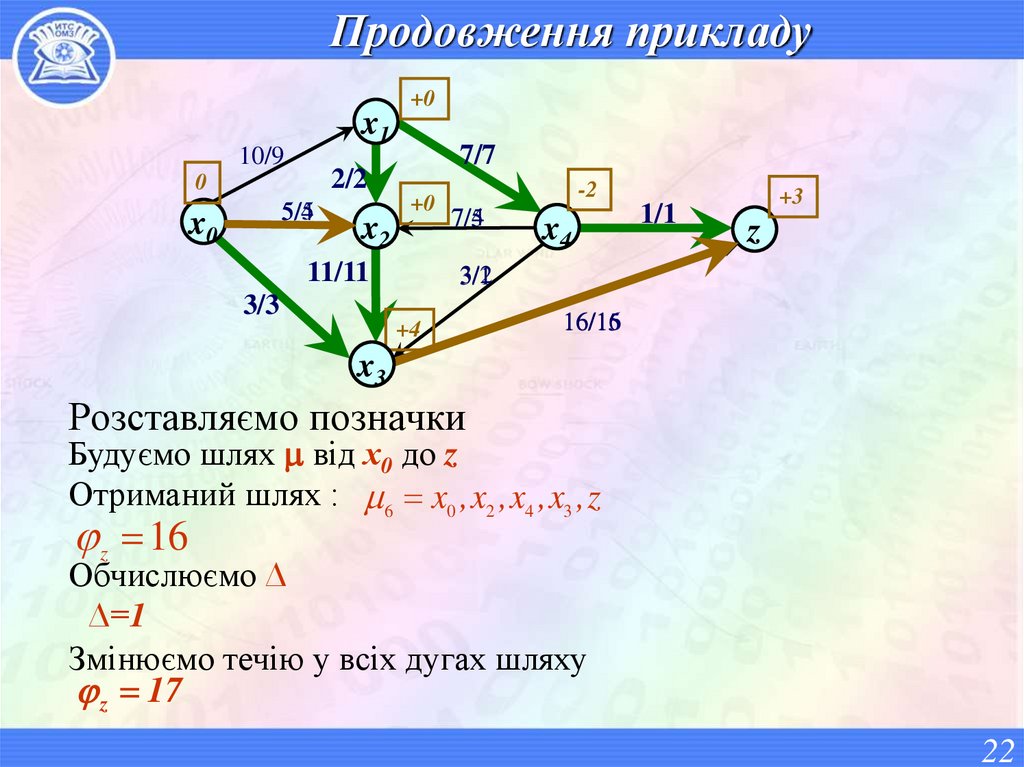
Розставляємо позначки
Будуємо шлях від х0 до z
Отриманий шлях : 6 x0 , x2 , x4 , x3 , z
z 16
Обчислюємо ∆
∆=1
Змінюємо течію у всіх дугах шляху
z 17
22
23. Продовження прикладу
x110/9
7/7
2/2
0
x0
+0
5/5
+0
x2
11/11
-2
7/6
x4
3/2
3/3
+4
x3
16/16
1/1
+3
z
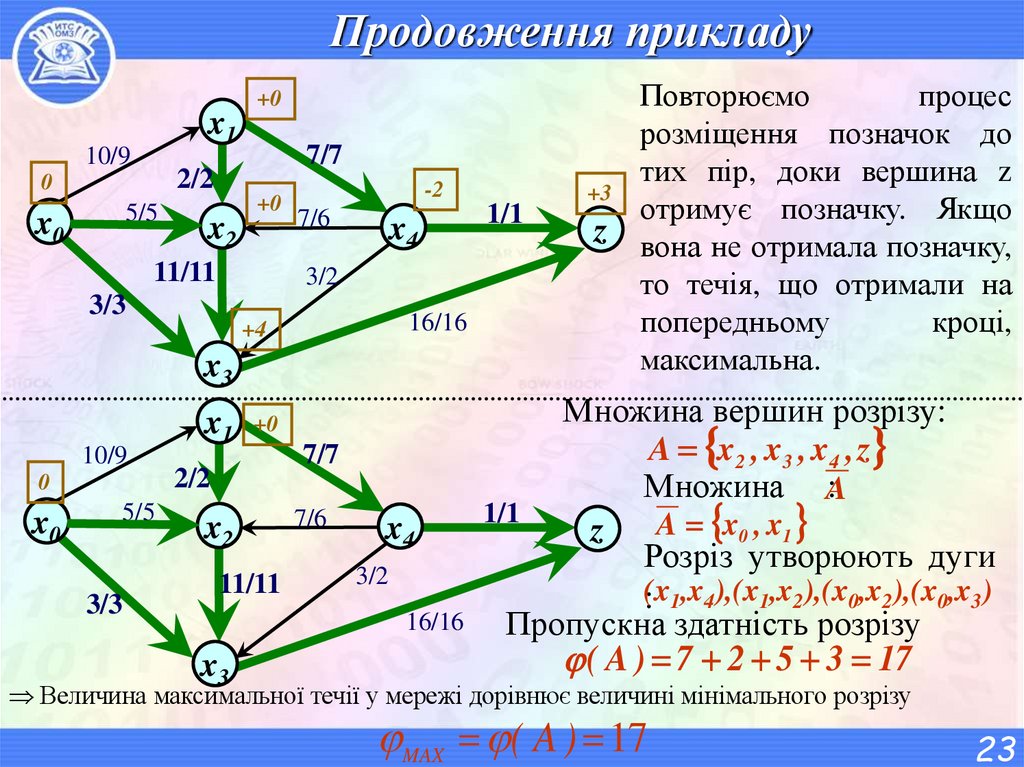
Повторюємо
процес
розміщення позначок до
тих пір, доки вершина z
отримує позначку. Якщо
вона не отримала позначку,
то течія, що отримали на
попередньому
кроці,
максимальна.
Множина вершин розрізу:
A x2 , x3 , x4 , z
7/7
10/9
2/2
0
Множина A
:
5/5
1/1
7/6
x0
A x0 , x1
x2
x4
z
Розріз утворюють дуги
3/2
11/11
(x
: 1,x4),(x1,x2),(x0,x2),(x0,x3)
3/3
16/16
Пропускна здатність розрізу
( A ) 7 2 5 3 17
x3
x1 +0
Величина максимальної течії у мережі дорівнює величині мінімального розрізу
MAX ( A ) 17
23