L_15

1.

Это написали к прошлой лекции
Опр. Определение предела функции по Гейне
(на языке последовательностей).
Пусть y=f(x) определена в Ů(x0, ε). Число А называется пределом функции
f(x) в т. x0 при x→x0, если
∀{xn} ∈ Ů(x0, ε)
То есть верно равенство
из
xn→x0 ⇒
lim f ( xn ) A
f( xn ) → A.
n
Замечание: Определение по Коши равносильно определению по Гейне
Следствия из замечания:
1. Функция f(x) не может иметь двух пределов, т.к. сходящаяся
последовательность f(xn) имеет 1 предел.
2. Все свойства, характерные для предела последовательности, будут
иметь место и для предела функции.
пропустить 10 строк

2.

Это написали к прошлой лекции
Свойства пределов функции
1. О локальной ограниченности.
Пусть lim
x x0
f ( x) A . Тогда ∃ U( x0 , e ), в которой |f( x )| ≤ M.
2. Об устойчивости знака функции.
Пусть lim f ( x) A 0. Тогда ∃ U( x0 , e ), в которой
x x 0
sign( f(x) )= sign A.
3. Если y = f ( x ) имеет предел, то ее можно представить как сумму
постоянной, равной этому пределу и б.м.
lim f ( x) A
x x 0
f ( x) A ( x), где ( x) б.м.
4. Об арифметических операциях.
Пусть
и
lim f ( x) A
а) lim[ f ( x) g ( x)] A B
lim g ( x) B. Тогда
b) lim[ f ( x) g ( x)] A B
x x 0
x x 0
x x 0
x x 0
f ( x) A
c) lim
,
x x 0 g ( x)
B
B 0

3.

Это написали к прошлой лекции
О предельном переходе
5. Пусть ∀x∈ Ů(x0, d) f ( x ) ≤ g ( x ),
Тогда, A ≤ B
6. Пусть ∀x∈ Ů(x0, d)
Тогда lim F ( x) A
lim f ( x) A
x x 0
lim g ( x) B
x x 0
f ( x ) ≤ F ( x ) ≤ g ( x ) и lim f ( x) lim g ( x) A
x x 0
x x 0
x x 0
7. О пределе сложной функции.
Пусть существуют конечные пределы
lim f ( x) b
x x 0
Пусть ∀x∈ Ů( x0, d) f( x ) ≠ b (т.е. f(x) не const.).
lim F ( y) A
y b
Тогда в точке x0 существует предел сложной функции F ( f (x) ) и
lim F ( f ( x)) lim F ( y)
x x 0
y b

4.

Это написали к прошлой лекции
8. Имеют место аналогичные свойства б.м. и б.б. функций.
б.м. функции
1
а) если ( x ) – б.м., то ( x)
– б.б.
б) ( x ) + b ( x ) + … + t ( x ) = g ( x ) – сумма конечного числа б.м. есть б.м.
в) ( x ) .M( x ) = b ( x ) – произведение б.м. на ограниченную есть б.м.
г) ( x ) . b ( x ) = g ( x ) – произведение б.м. на б.м. есть б.м.
д) ( x ) . с = g ( x ) – произведение б.м. на const есть б.м.
б.б. функции
е) F ( x ) + G ( x ) = R ( x ) – сумма б.б. одного знака есть б.б.
ж) F ( x ) .M( x ) = R ( x ) – произведение б.б. на ограниченную и ≠ 0 есть б.б.
з) F ( x ) + M ( x ) = R ( x ) – сумма б.б. и ограниченной есть б.б.
пропустить 20 клеточек

5. Опр. Число А называется правосторонним пределом f(x), если

Это Новое
§ 4. Односторонние пределы
Опр. Число А называется правосторонним пределом f(x), если
по Коши: ∀e>0 ∃d(e) ∀x∈R: 0 < x - x0 < d выполняется | f(x) – A | < e
по Гейне: ∀ { xn }: xn > x0 , xn → x0 при n →∞ выполняется f( xn ) → A
lim f ( x) A
x x0
Опр. Число А называется левосторонним пределом f(x), если
по Коши: ∀e>0 ∃d(e) ∀x∈R: - d < x - x0 < 0 выполняется | f(x) – A | < e
по Гейне: ∀ { xn }: xn < x0 , xn → x0
при n →∞ выполняется f( xn ) → A
lim f ( x) A
x x0

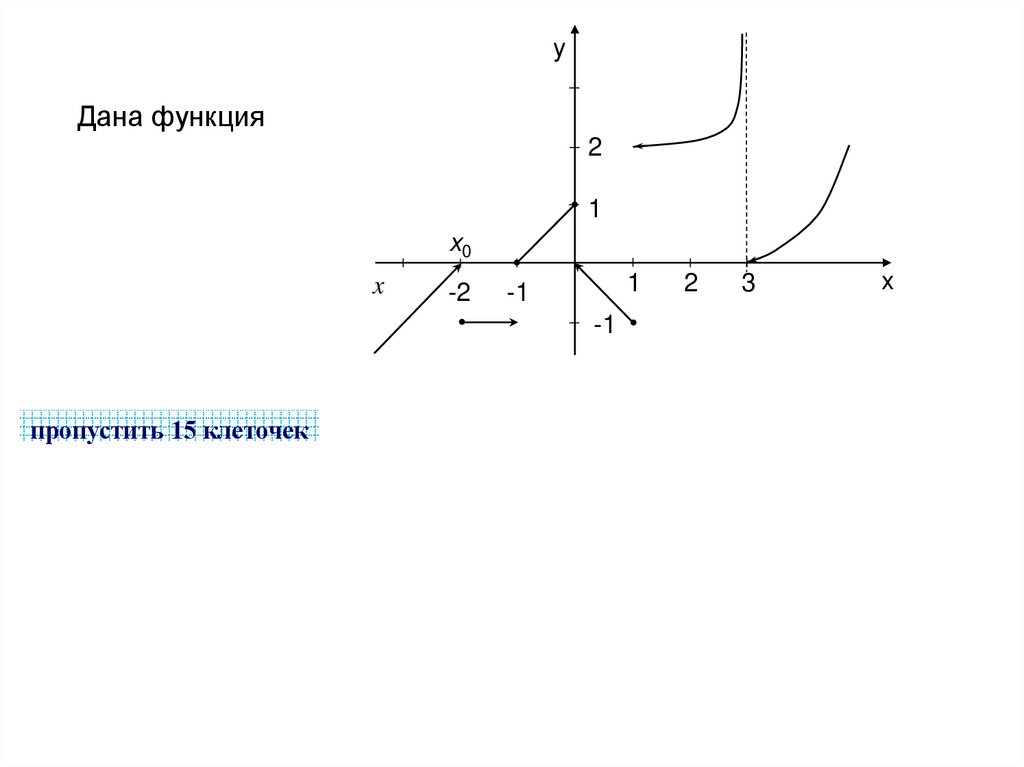
6. Дана функция

y
Дана функция
2
1
x0
x
-2
1
-1
-1
пропустить 15 клеточек
2
3
x

7. Доказательство:

Теорема (о существовании предела)
Для того, чтобы существовал предел lim f ( x) необходимо и достаточно, чтобы
x x 0
существовал левосторонни и правосторонний пределы f(x) и они оба были равны.
В этом случае их значение и является двусторонним пределом f(x) в точке x0.
lim f ( x) A lim f ( x) lim f ( x) A
x x 0
Доказательство:
x x 0
пропустить 0.5 страницы
x x 0