Similar presentations:
lec0_fe-theory
1. Основы теории метода конечных элементов
Вдовин Денис Сергеевич, к.т.н., доцент кафедры СМ10 «Колесныемашины» и СМ9 «Многоцелевые гусеничные машины и мобильные
роботы
МГТУ им. Н.Э. Баумана
2. Литература и полезные ссылки
• Сопромат:• https://www.youtube.com/channel/UCuDftnpHxCjOute8eTyR3Fg
• Феодосьев В.И. Сопромат.
http://pnu.edu.ru/media/filer_public/2013/04/10/212_fedosev_sopromat_1999.pdf
• http://mysopromat.ru/
• Софт по МКЭ:
• NX CAE пособие
http://media.plm.automation.siemens.com/ru_ru/nx/book/NX-AdvancedSimulation-Prakticheskoe-Posobie.pdf
• Help Altair Optistruct (getting started & tutorials)
• Help Ansys Workbench (getting started & tutorials)
• Help NX.CAST (сборник примеров к NX)
3. Система оценки знаний (что надо, чтобы сдать экзамен?)
• Посетить лекции и сделать лабы.• Выполнить вариант ДЗ и его защитить.
• Сдать модули два раза в течение семестра (ответить на теор.вопросы и
решить задачу на компе).
• Сдать экзамен (2 теор.вопроса + задача на компе).
Баллы:
• модуль №1 – 15 баллов
• модуль №2 – 15 баллов
• ДЗ – 40 баллов
• Экзамен – 30 баллов
Баллы
Итог в зачетку:
85 – 100
отлично
71 - 84
хорошо
60 – 70
удовлетворительно
0-59
неудовлетворительно
4. Вариация функции
Приращение функцииВариация функции
5. Функционал, вариация функционала
Интеграл функции(заштрихованная область под графиком)
Интеграл это «функция функции» = Функционал
Вариация функционала
дважды (заштрихованная область под графиком)
6. Принцип Лагранжа – минимум потенциальной энергии
Пластинка единичной толщины:7. Принцип Лагранжа – минимум потенциальной энергии
Работа поверхностных сил:Работа объемных сил:
- сумма работ объемных и поверхностных сил
Работа внутренних сил:
8. Принцип Лагранжа – минимум потенциальной энергии
Вариация потенциальной энергии элемента пластинкиПринцип возможных работ: при равновесии сумма всех
возможных работ на всех возможных перемещениях
равна нулю.
Обозначим:
Тогда:
- потенциальная энергия системы
- потенциальная энергия деформации тела
- работа внешней нагрузки на действительных перемещениях
9. Принцип Лагранжа – минимум потенциальной энергии
Обозначим:уменьшение потенциала внешней нагрузки при
переходе тела из недеформированного состояния в
деформированное
Потенциальная энергия системы:
Условие экстремума:
Принцип
Лагранжа:
из
всех
возможных
перемещений
(деформированных состояний) реализуются именное те, при которых
потенциальная энергия системы минимальна.
10. Метод конечных элементов
δП(v)=0v – множество функций, описывающих всевозможные перемещения тела
w – та функция из v, в которой П минимальна (искомые перемещения)
Точное нахождение минимума П(v) эквивалентно решению
дифференциального уравнения теории упругости и является
бесконечномерной задачей. Идея сеточных методов состоит в
замене бесконечномерной задачи n-мерной, т.е. в переходе к
дискретной модели.
11. Метод конечных элементов
1. В рассматриваемой области упругого тела фиксируется конечное числоточек. Эти точки называются узлами.
2. Значение непрерывной функции v в каждом узле считается переменной,
которая должна быть определена.
3. Область разбивается на конечное число подобластей, называемых
элементами. Эти элементы имеют общие узлы и в совокупности
аппроксимируют форму упругого тела.
4. На каждом элементе непрерывная функция v аппроксимируется
полиномиальными функциями
, называемыми функциями формы,
значения которых внутри элемента и на его границах определяются через
значения функции в узлах. Здесь индекс k относится к элементу, а индекс i
– к узлу.
12. Метод конечных элементов
13. Метод конечных элементов
14. Метод конечных элементов
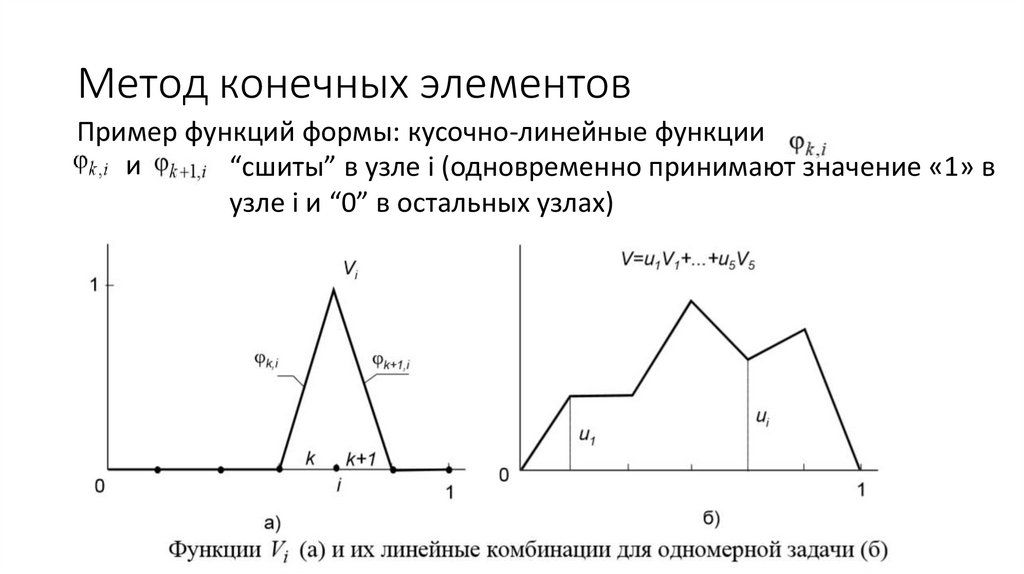
Пример функций формы: кусочно-линейные функциии
“сшиты” в узле i (одновременно принимают значение «1» в
узле i и “0” в остальных узлах)
15. Метод конечных элементов
Решение:Условие минимума
функционала П(V):
Деформации:
Напряжения:
L – оператор дифференцирования,
который переводит перемещения в
деформации
S – матрица Гука, переводящая
деформации в напряжения
16. Метод конечных элементов
Энергия деформации:Обозначим:
Энергия деформации:
тогда:
17. Метод конечных элементов
Потенциал внешних нагрузок:(r – включает все внешние нагрузки: объемные, поверхностные,
сосредоточенные)
Обозначим:
тогда, в матричной форме:
18. Метод конечных элементов
Полная потенциальная энергия системы:Условие равенства нулю вариации
полной потенциальной энергии:
Уравнение для определения параметров Ритца:
К – матрица глобальной жесткости
{u} – вектор перемещений (вектор неизвестных)
{R} – вектор нагрузок