МТС презентация 6

1. Сетевые модели. Сети Петри (N-схемы)

1
Число и расположение маркеров могут изменяться при
выполнении сети Петри. Под выполнением сети Петри
понимается
последовательность
запусков
переходов.
Формальное определение: переход tj в сети с маркировкой µ
разрешен, если для всех рi Р µ(рi) ≥ F(рi,tj), где µ(рi) –
количество маркеров в позиции рi. рi Р µ(рi) ≥ F(рi,tj),
Переход запускается удалением маркеров из его входных
позиций и добавлением маркеров в выходные позиции
перехода. Переход может запускаться только в том случае,
если он разрешен. Переход называется разрешенным, если
каждая из его входных позиций имеет число маркеров, по
крайней мере, равное числу дуг из позиции в переход.
Маркеры во входных позициях, которые разрешают переход,
называются его разрешающими маркерами.

2. Сетевые модели. Сети Петри (N-схемы)

2
При запуске перехода из входных позиций удаляются
разрешающие маркеры в количестве, соответствующем числу
исходящих из позиций в переход дуг, и последующим
помещением в каждую из его выходных позиций по одному
маркеру для каждой выходящей из перехода дуги.
В общем случае запуск перехода tj заменяет маркировку
сети Петри µ на новую маркировку µ', определяемую
соотношением µ'(рi) = µ(рi) – F(рi,tj) + H(рi,tj).
Поскольку запускаться могут только разрешенные
переходы, для которых µ(рi) ≥ F(рi,tj), рi Р, то число маркеров в
любой позиции будет оставаться неотрицательным.
Если в какой-либо момент времени разрешено несколько
переходов, то следующим запускаемым переходом может
быть любой из них. Это свойство сетей Петри отражает
неоднозначность порядка возникновения событий, связанных
с параллельно протекающими процессами.

3. Сетевые модели. Сети Петри (N-схемы)

3
Другая важная особенность сетей Петри – их асинхронная
природа. Сети Петри не обладают какими-либо средствами,
отражающими течение времени или фиксирующими
некоторые моменты времени. Однако они предоставляют
возможность отображать частичный порядок возникновения
событий, т.е. обладают важным свойством отражения
относительного времени протекания процессов путем
установления причинно-следственной связи событий.
Средства установления причинно-следственных связей
событий позволяют моделировать важные свойства систем
логического управления – параллелизм и конфликтные
ситуации. Параллелизм моделируется в сети Петри
независимыми разрешенными переходами. В конфликтной
ситуации разрешенные переходы имеют общий разрешающий
маркер, и поэтому запуск одного перехода удаляет общий
маркер и таким образом запрещает другой переход.

4. Сетевые модели. Сети Петри (N-схемы)

4
Одним из методов анализа сетей Петри является
построение дерева достижимости. Дерево достижимости – это
граф вершинами которого являются достижимые маркировки.
Начальной маркировке µ0 соответствует корневая вершина.
Если из вершины µ в вершину µ' ведет дуга, то она взвешена
переходом tj T, переводящим сеть Петри из маркировки µ в µ'
t
.
Если для некоторой маркировки ни один из переходов
сработать не может, то такая маркировка называется
тупиковой. Тупиковым маркировкам соответствуют висячие
вершины.
Маркировка µ' является достижимой из маркировки μ, если
существует такая последовательность переходов τ=(t1, t2, …, tk),
что
t
t
t
j
1
...
1
2
k

5. Сетевые модели. Сети Петри (N-схемы)

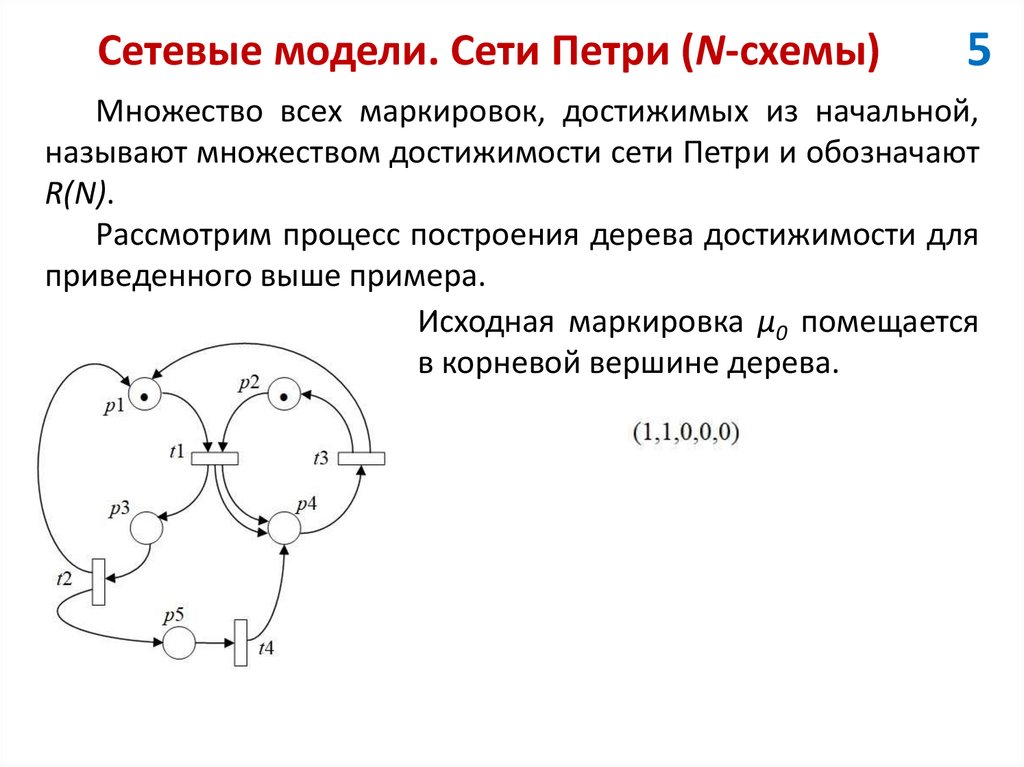
5
Множество всех маркировок, достижимых из начальной,
называют множеством достижимости сети Петри и обозначают
R(N).
Рассмотрим процесс построения дерева достижимости для
приведенного выше примера.
Исходная маркировка µ0 помещается
в корневой вершине дерева.

6. Сетевые модели. Сети Петри (N-схемы)

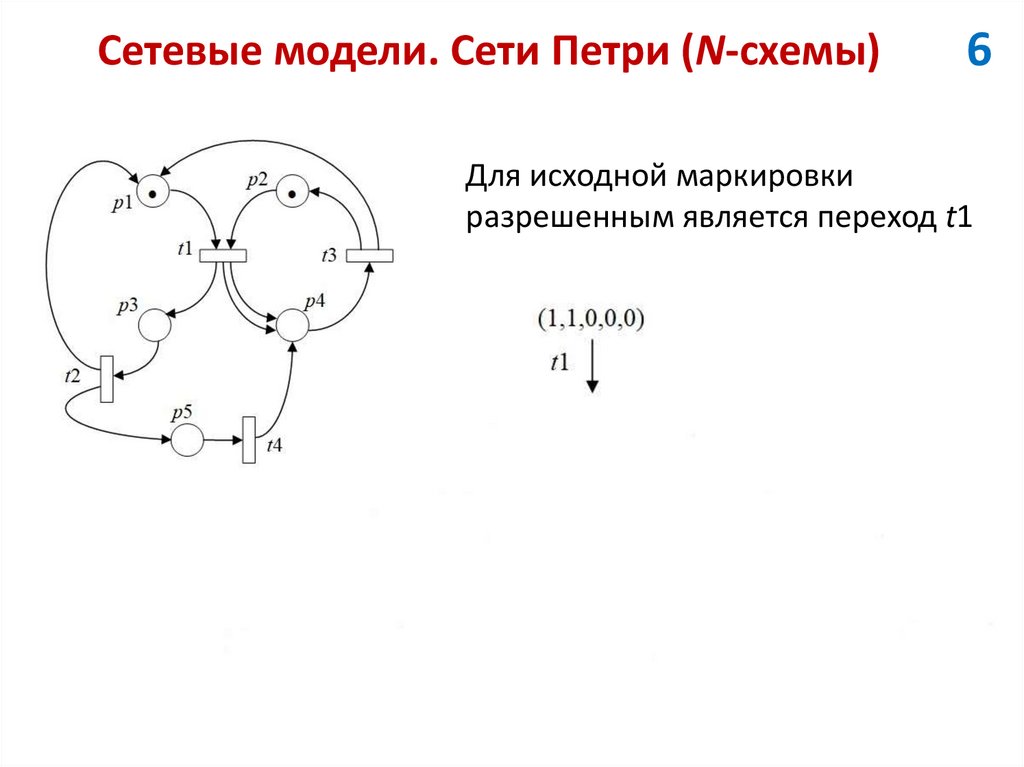
6
Для исходной маркировки
разрешенным является переход t1

7. Сетевые модели. Сети Петри (N-схемы)

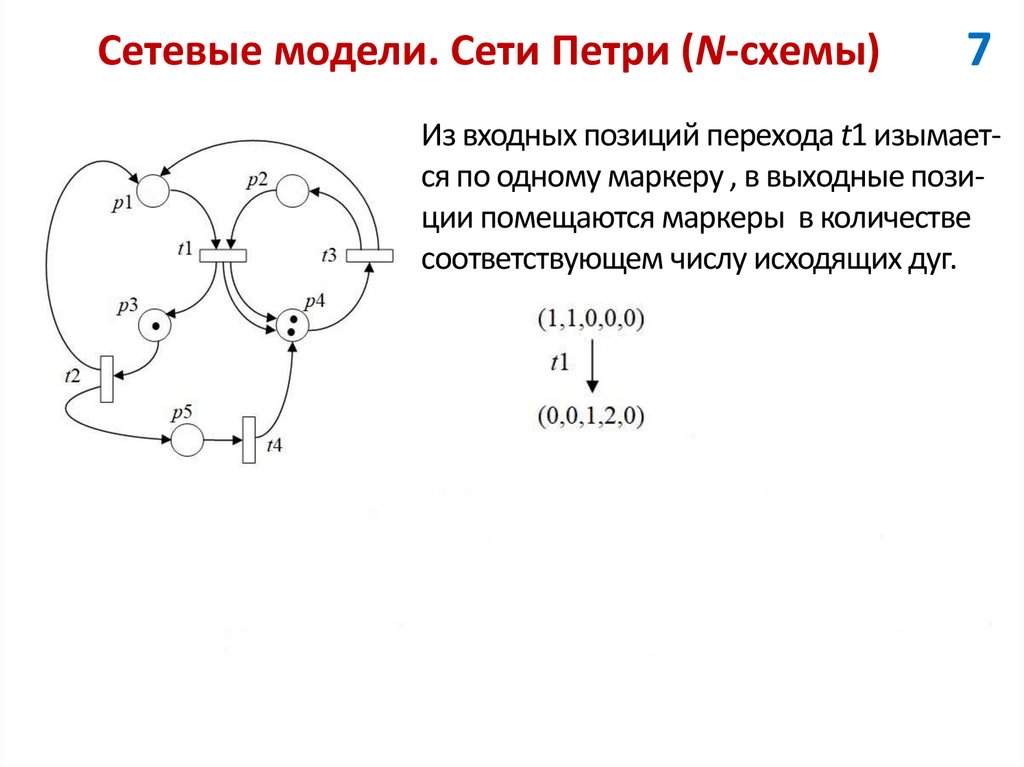
7
Из входных позиций перехода t1 изымается по одному маркеру , в выходные позиции помещаются маркеры в количестве
соответствующем числу исходящих дуг.

8. Сетевые модели. Сети Петри (N-схемы)

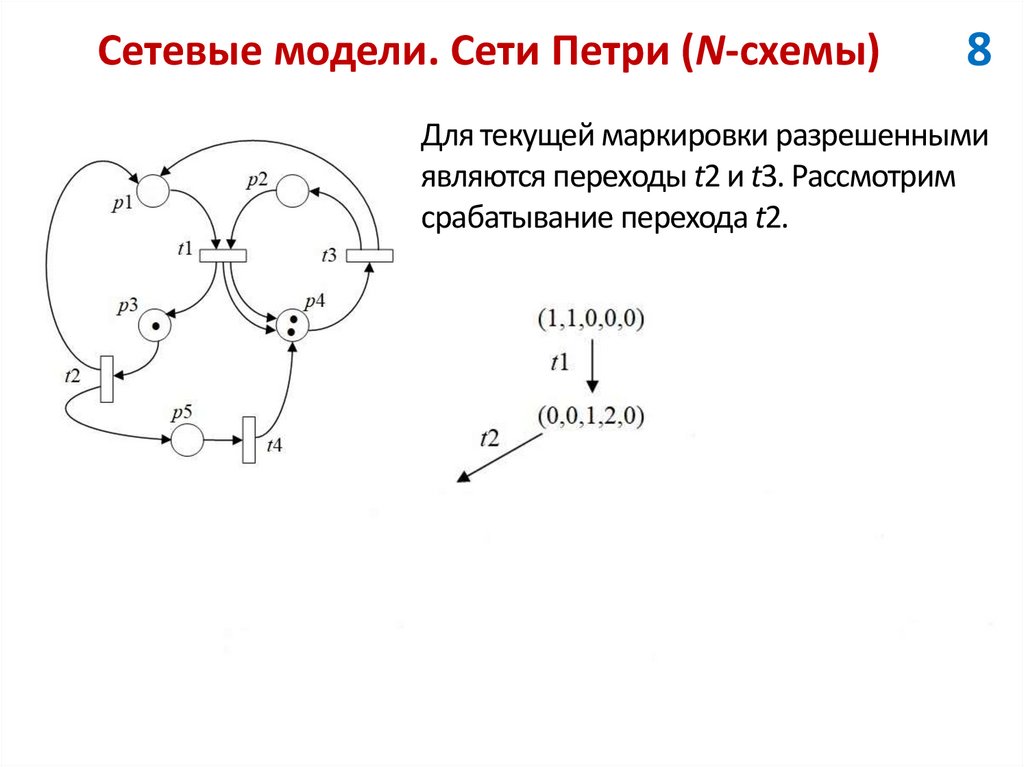
8
Для текущей маркировки разрешенными
являются переходы t2 и t3. Рассмотрим
срабатывание перехода t2.

9. Сетевые модели. Сети Петри (N-схемы)

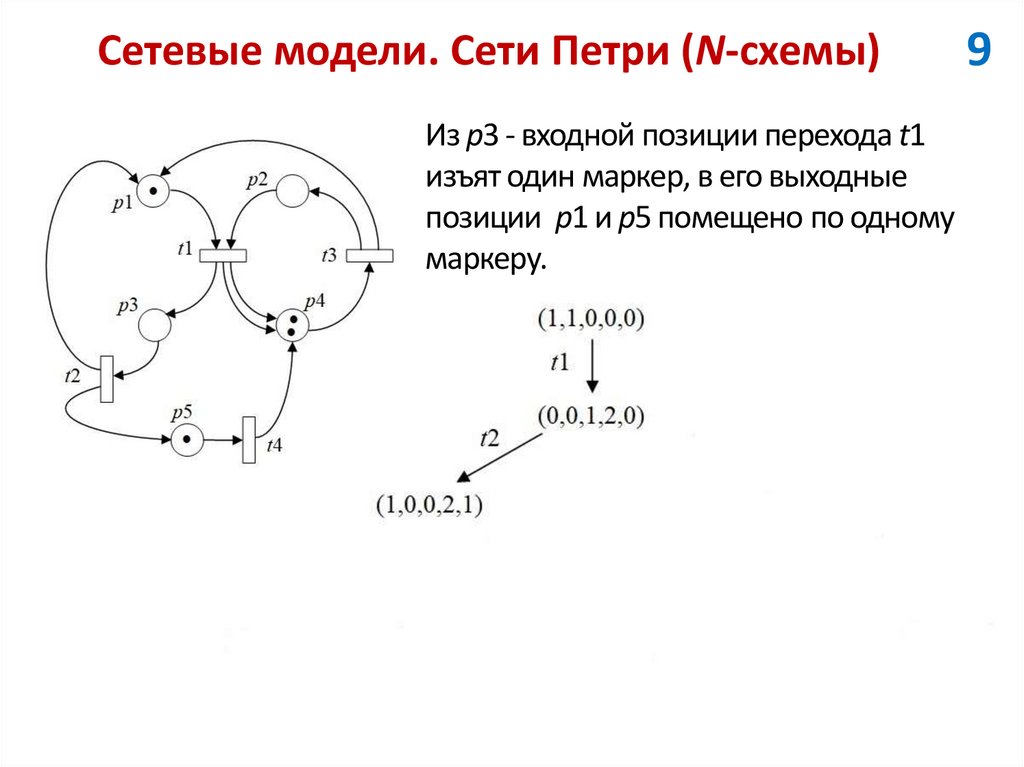
Из p3 - входной позиции перехода t1
изъят один маркер, в его выходные
позиции p1 и p5 помещено по одному
маркеру.
9

10. Сетевые модели. Сети Петри (N-схемы)

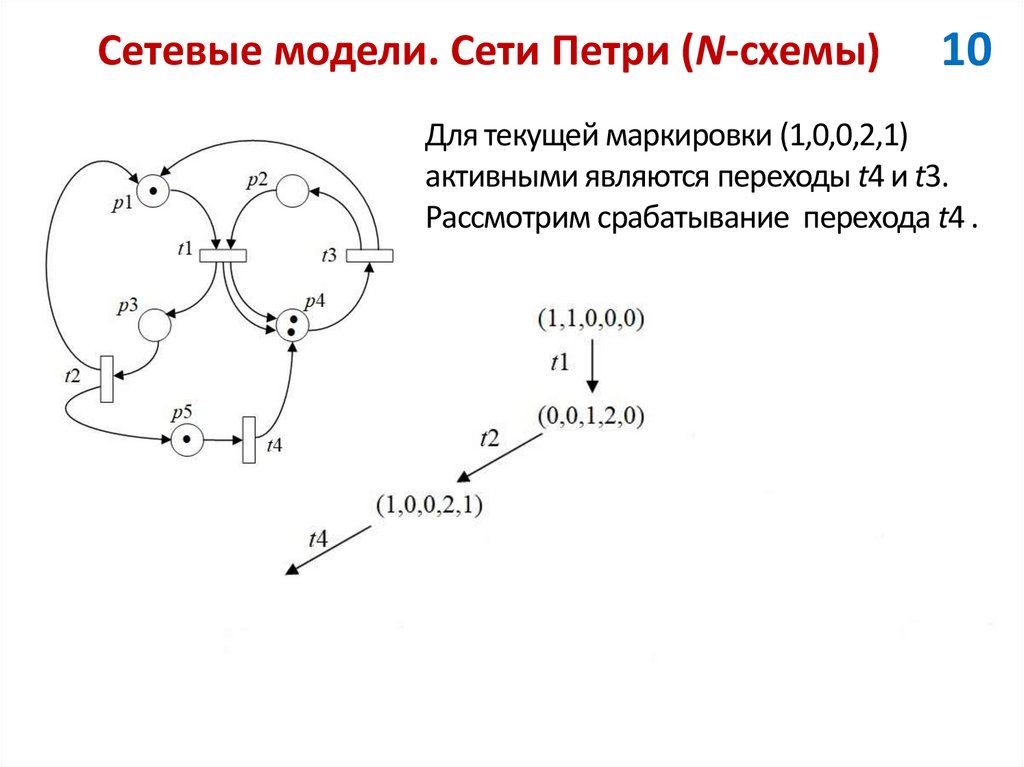
10
Для текущей маркировки (1,0,0,2,1)
активными являются переходы t4 и t3.
Рассмотрим срабатывание перехода t4 .

11. Сетевые модели. Сети Петри (N-схемы)

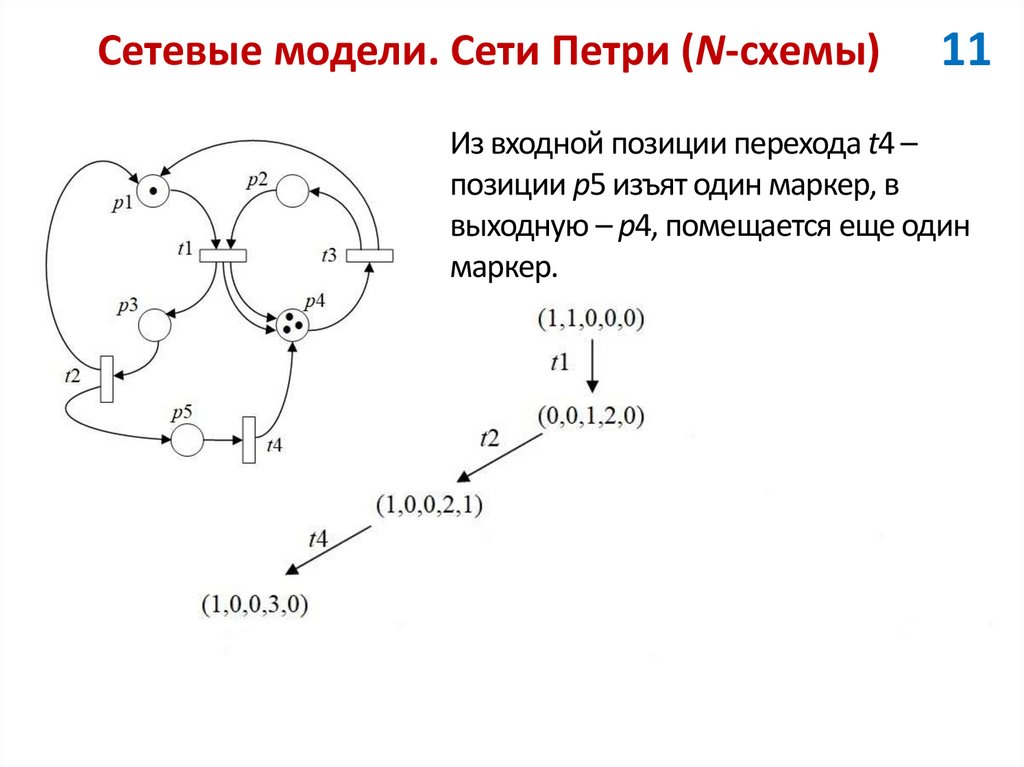
11
Из входной позиции перехода t4 –
позиции p5 изъят один маркер, в
выходную – p4, помещается еще один
маркер.

12. Сетевые модели. Сети Петри (N-схемы)

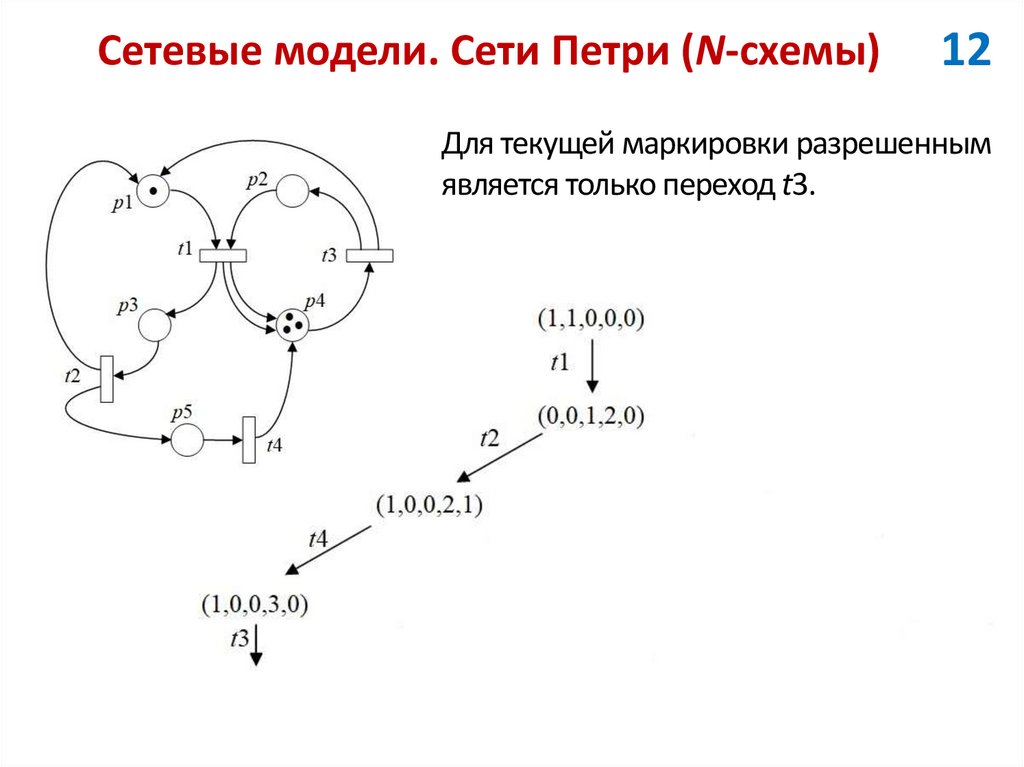
12
Для текущей маркировки разрешенным
является только переход t3.

13. Сетевые модели. Сети Петри (N-схемы)

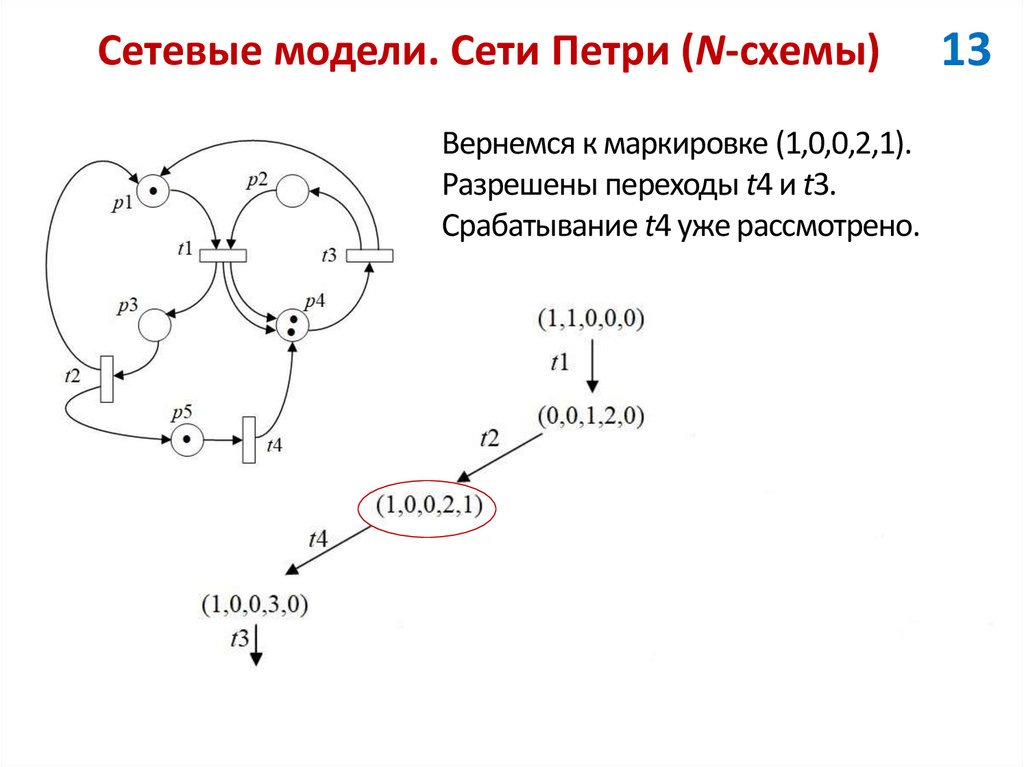
Вернемся к маркировке (1,0,0,2,1).
Разрешены переходы t4 и t3.
Срабатывание t4 уже рассмотрено.
13

14. Сетевые модели. Сети Петри (N-схемы)

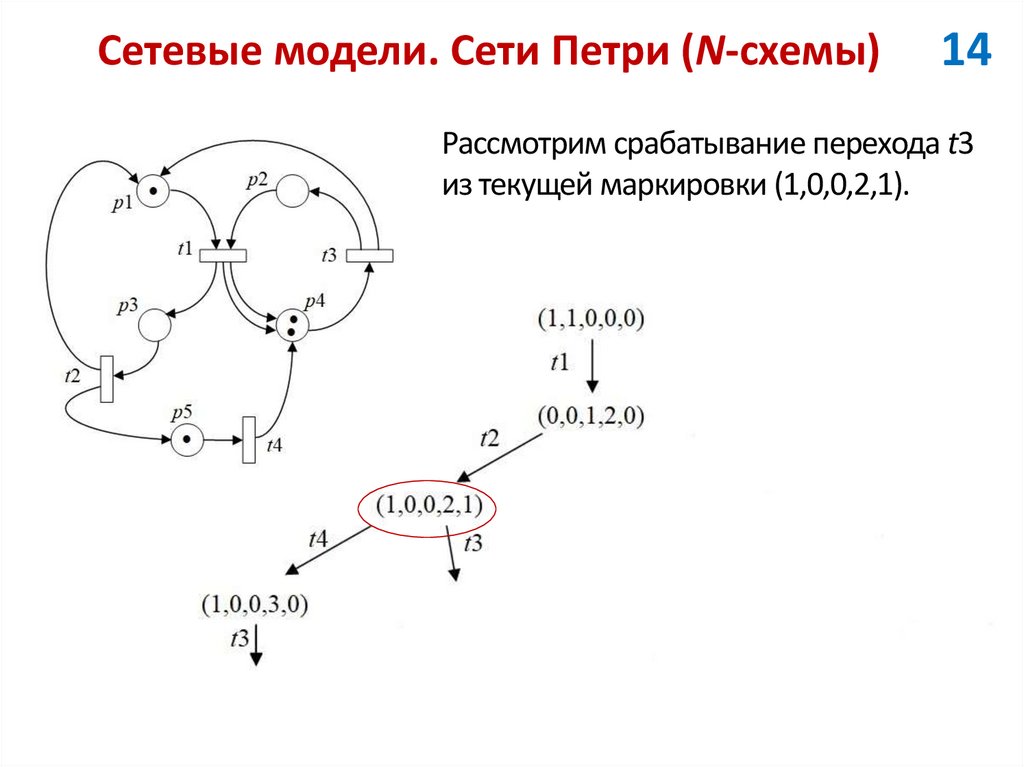
14
Рассмотрим срабатывание перехода t3
из текущей маркировки (1,0,0,2,1).

15. Сетевые модели. Сети Петри (N-схемы)

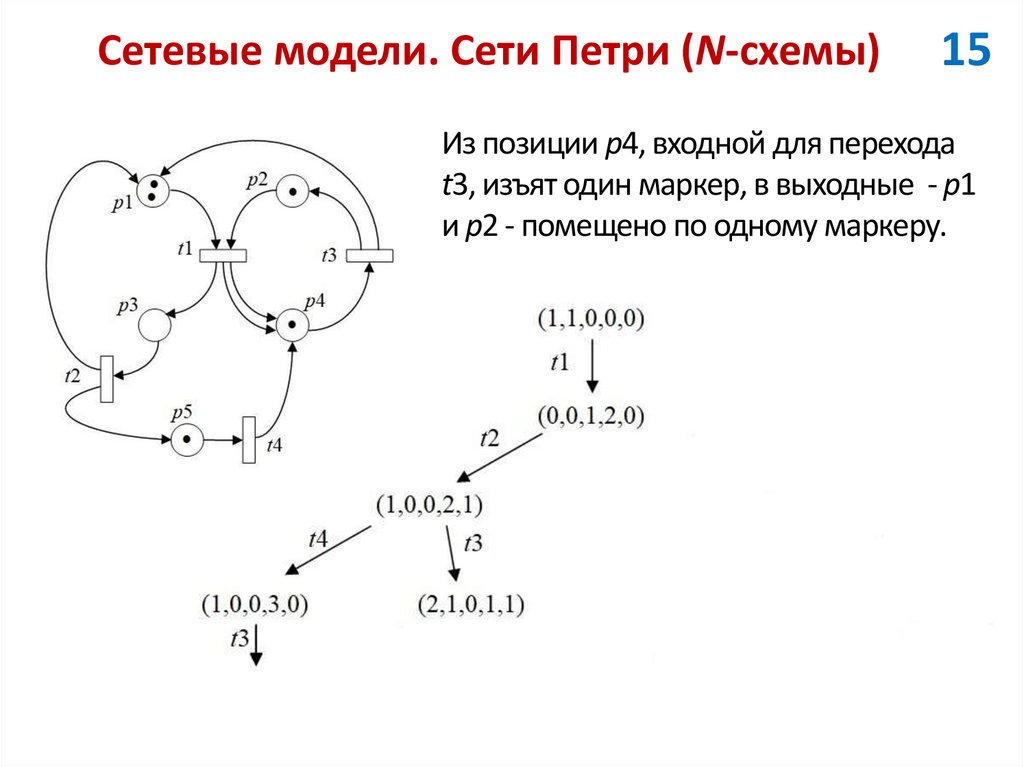
15
Из позиции p4, входной для перехода
t3, изъят один маркер, в выходные - p1
и p2 - помещено по одному маркеру.

16. Сетевые модели. Сети Петри (N-схемы)

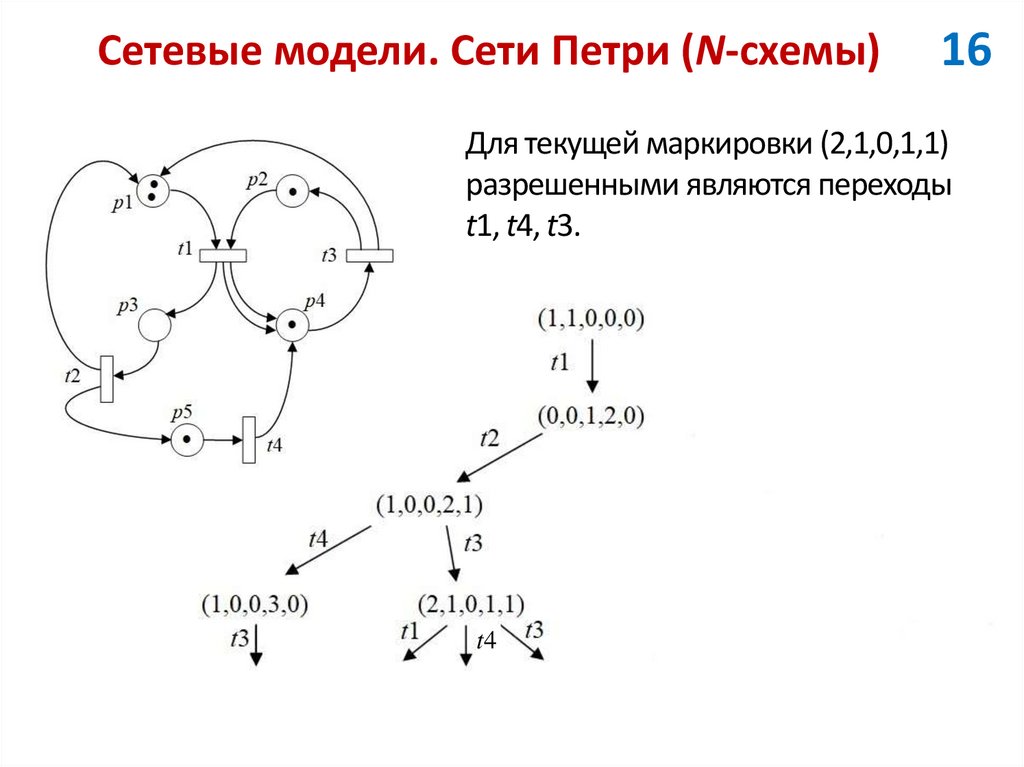
16
Для текущей маркировки (2,1,0,1,1)
разрешенными являются переходы
t1, t4, t3.
t4

17. Сетевые модели. Сети Петри (N-схемы)

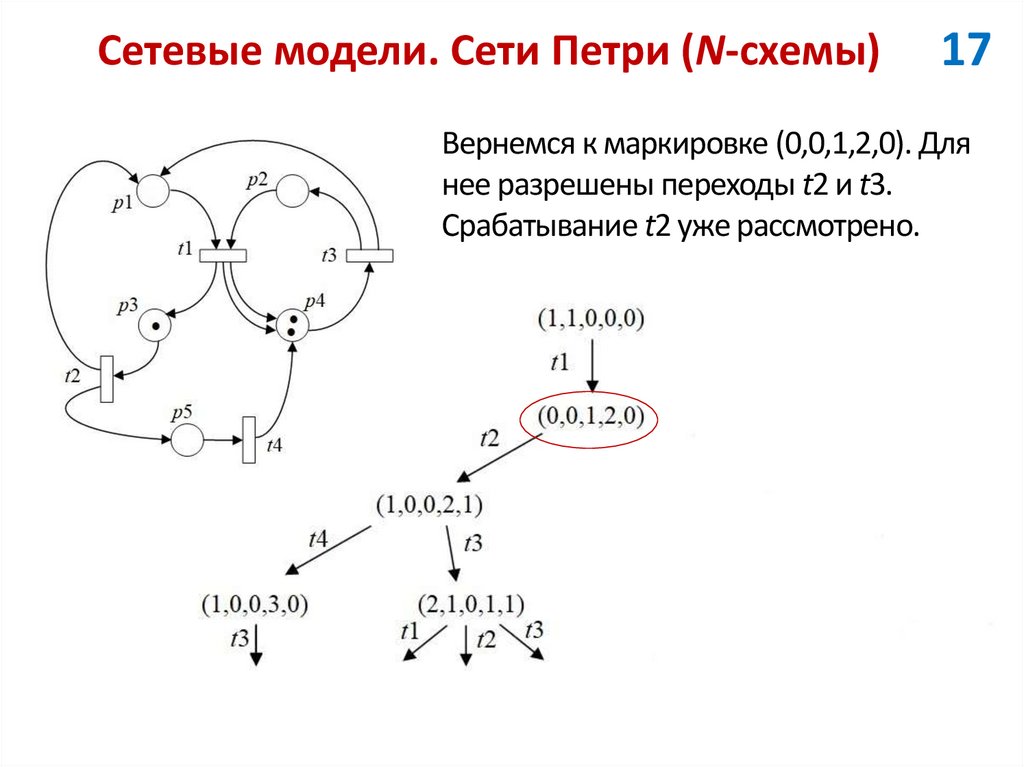
17
Вернемся к маркировке (0,0,1,2,0). Для
нее разрешены переходы t2 и t3.
Срабатывание t2 уже рассмотрено.

18. Сетевые модели. Сети Петри (N-схемы)

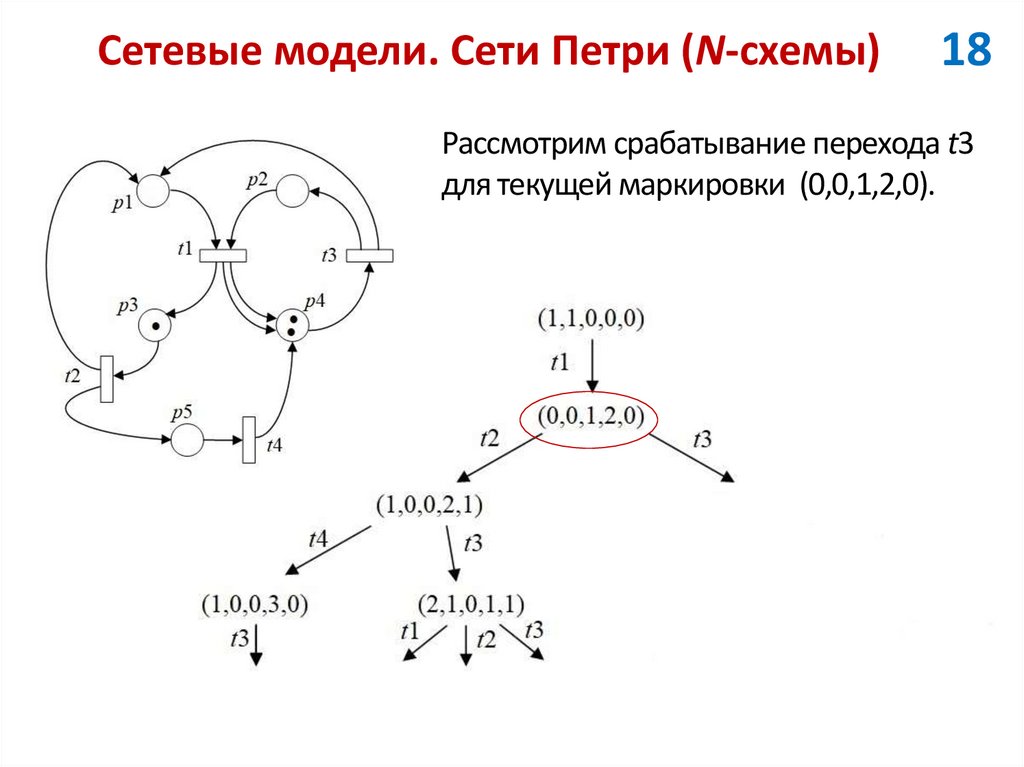
18
Рассмотрим срабатывание перехода t3
для текущей маркировки (0,0,1,2,0).

19. Сетевые модели. Сети Петри (N-схемы)

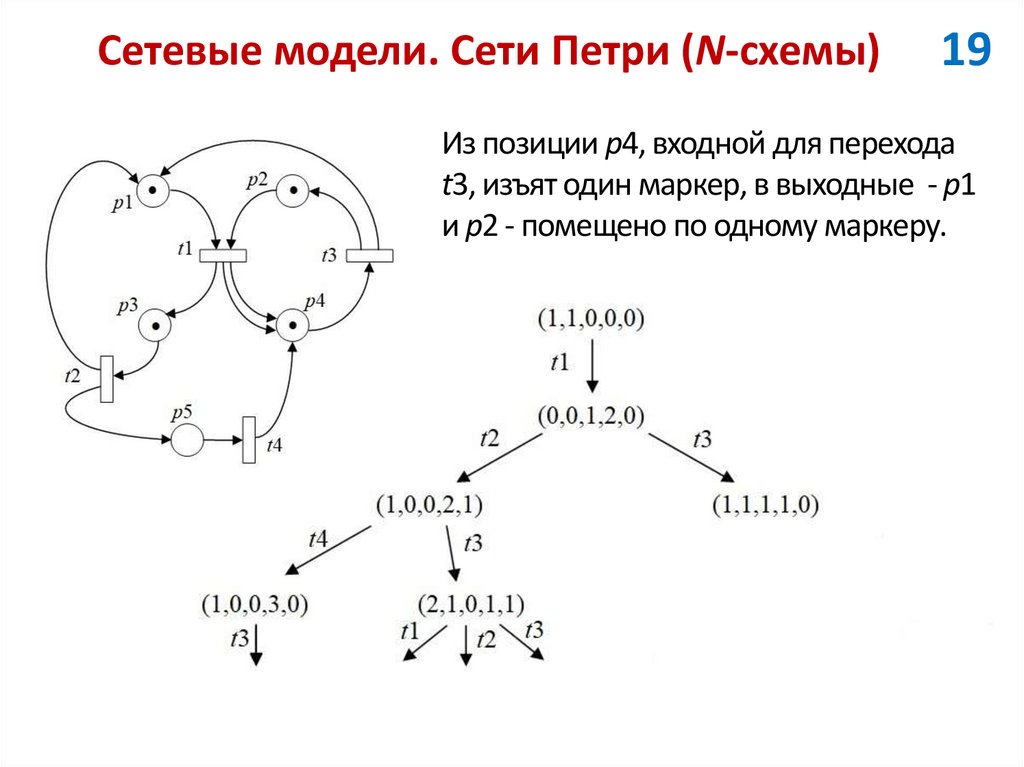
19
Из позиции p4, входной для перехода
t3, изъят один маркер, в выходные - p1
и p2 - помещено по одному маркеру.

20. Сетевые модели. Сети Петри (N-схемы)

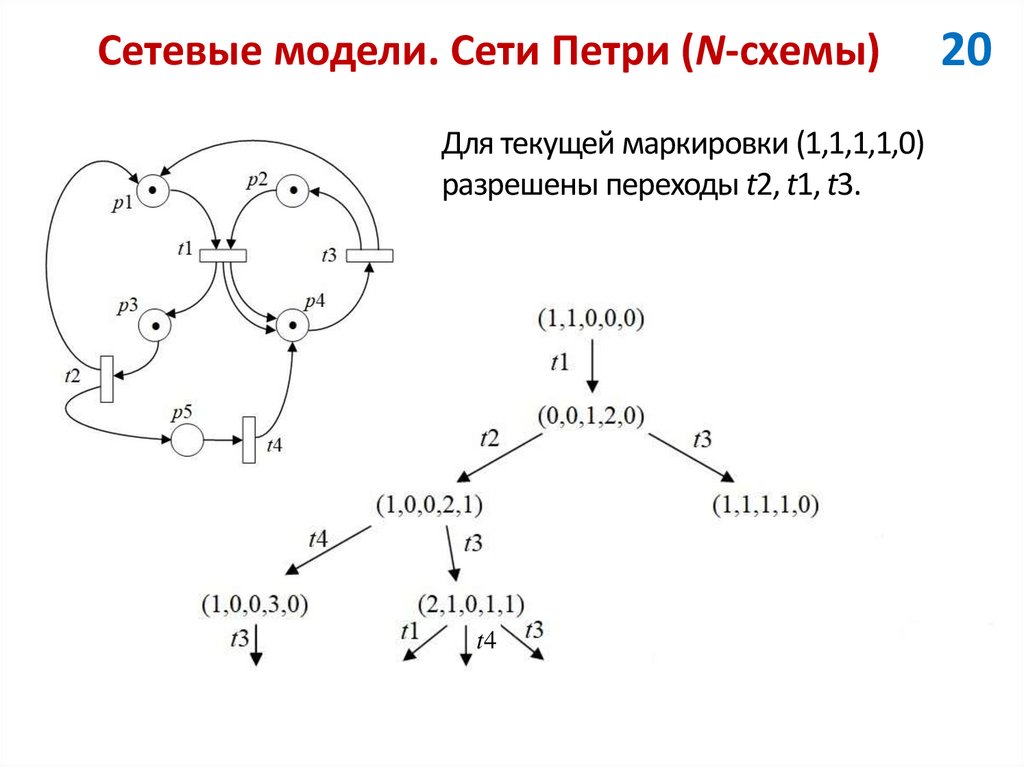
Для текущей маркировки (1,1,1,1,0)
разрешены переходы t2, t1, t3.
t4
20

21. Сетевые модели. Сети Петри (N-схемы)

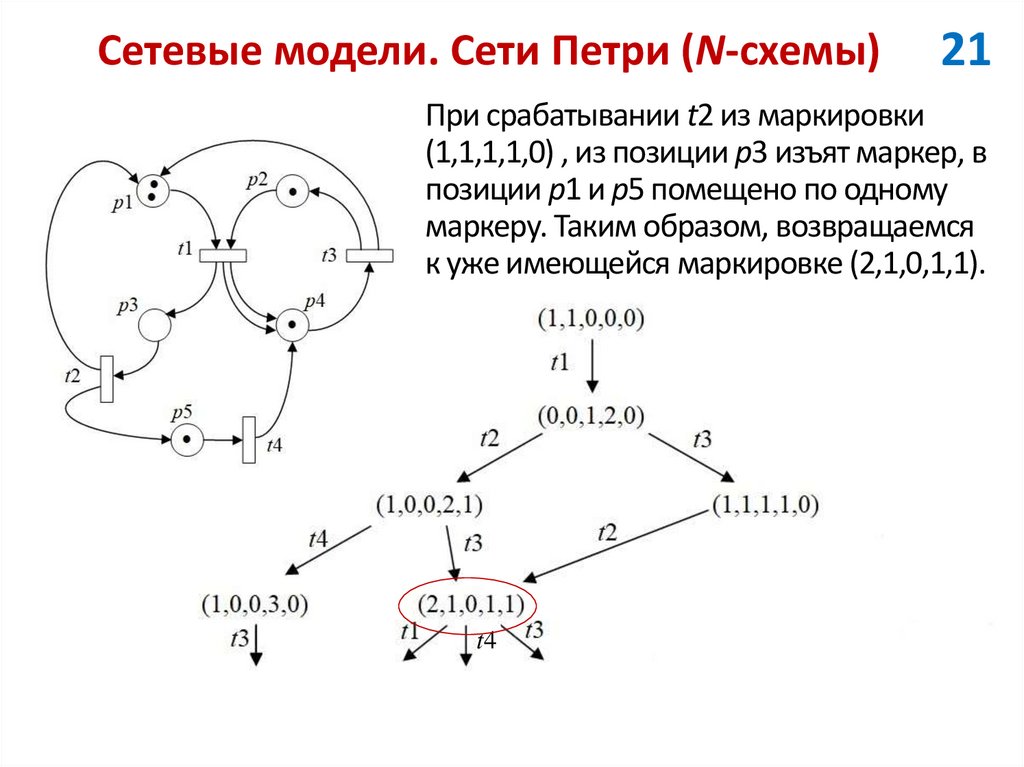
21
При срабатывании t2 из маркировки
(1,1,1,1,0) , из позиции p3 изъят маркер, в
позиции p1 и p5 помещено по одному
маркеру. Таким образом, возвращаемся
к уже имеющейся маркировке (2,1,0,1,1).
t4

22. Сетевые модели. Сети Петри (N-схемы)

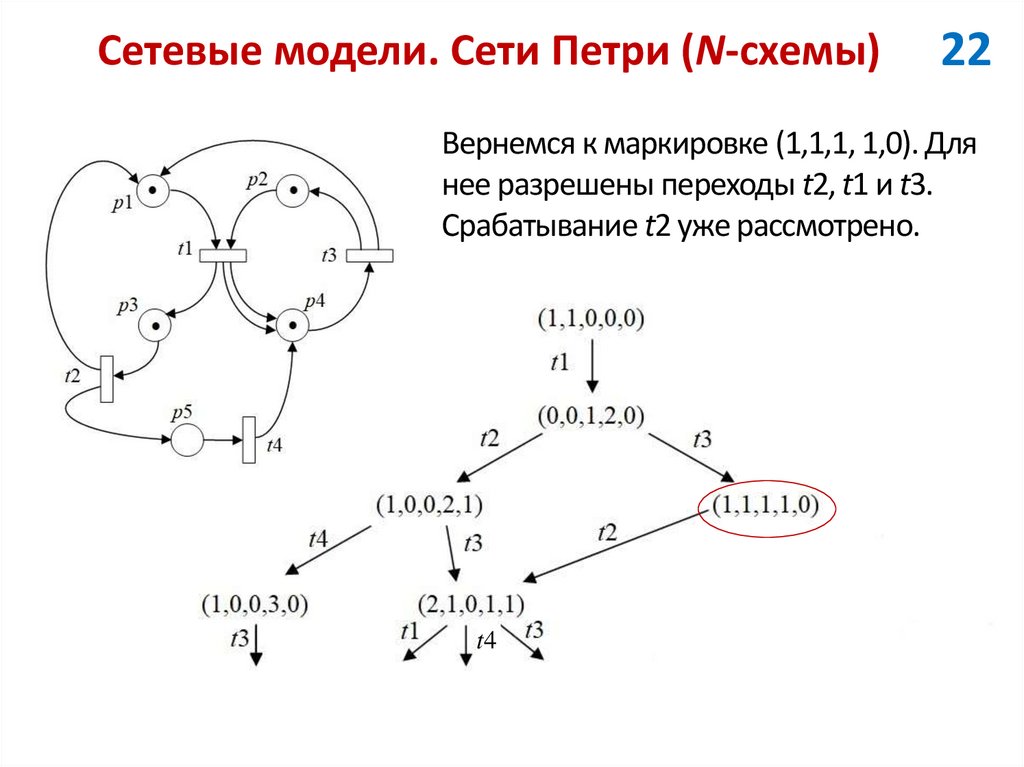
22
Вернемся к маркировке (1,1,1, 1,0). Для
нее разрешены переходы t2, t1 и t3.
Срабатывание t2 уже рассмотрено.
t4

23. Сетевые модели. Сети Петри (N-схемы)

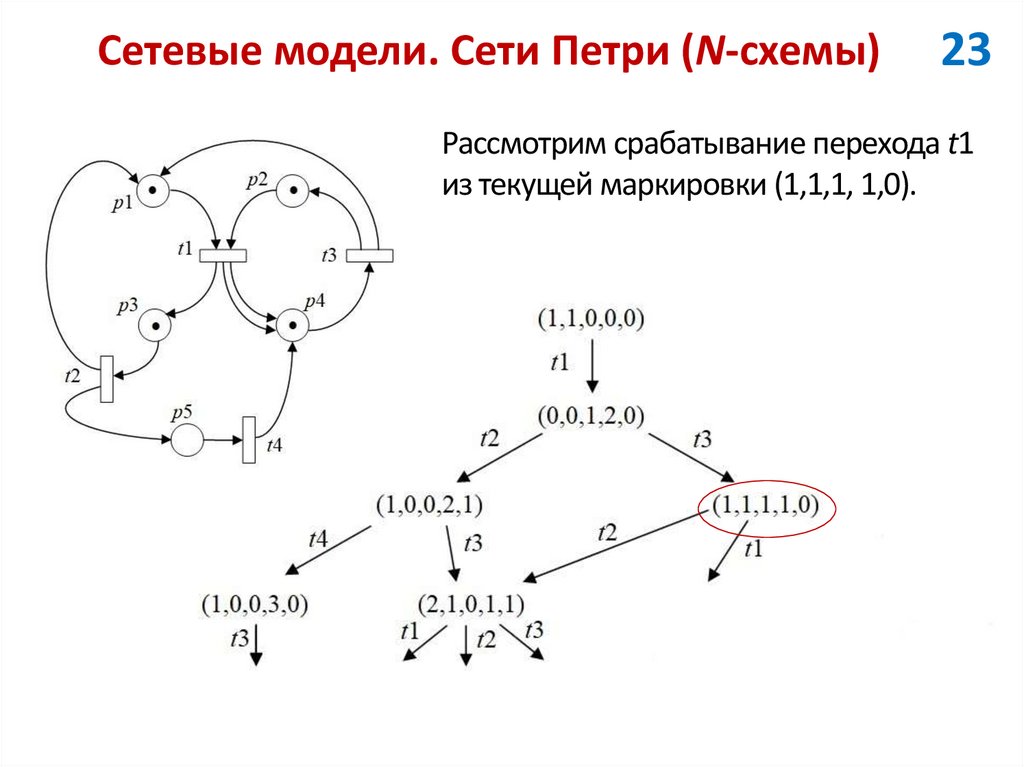
23
Рассмотрим срабатывание перехода t1
из текущей маркировки (1,1,1, 1,0).

24. Сетевые модели. Сети Петри (N-схемы)

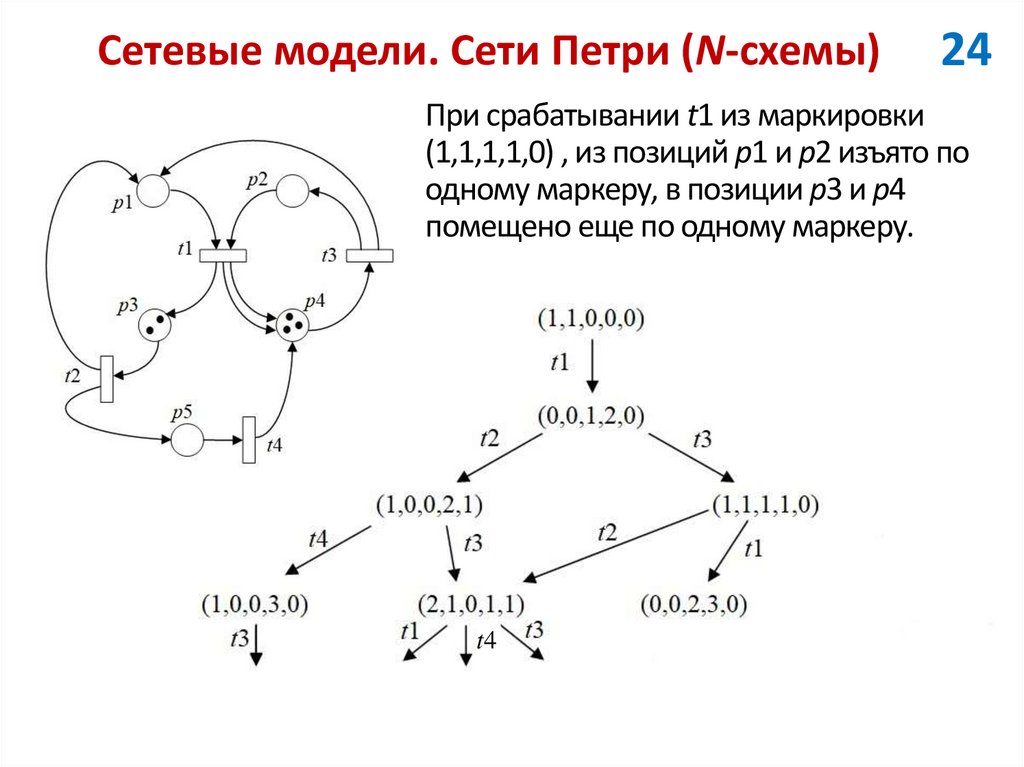
24
При срабатывании t1 из маркировки
(1,1,1,1,0) , из позиций p1 и p2 изъято по
одному маркеру, в позиции p3 и p4
помещено еще по одному маркеру.
t4

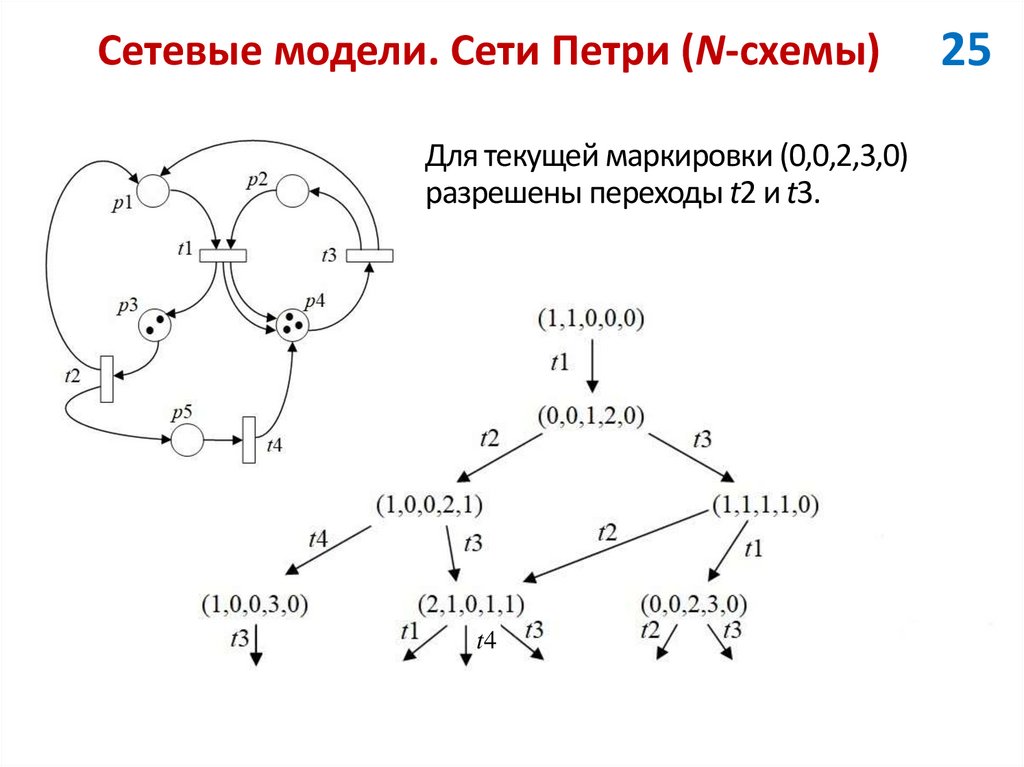
25. Сетевые модели. Сети Петри (N-схемы)

Для текущей маркировки (0,0,2,3,0)
разрешены переходы t2 и t3.
t4
25

26. Сетевые модели. Сети Петри (N-схемы)

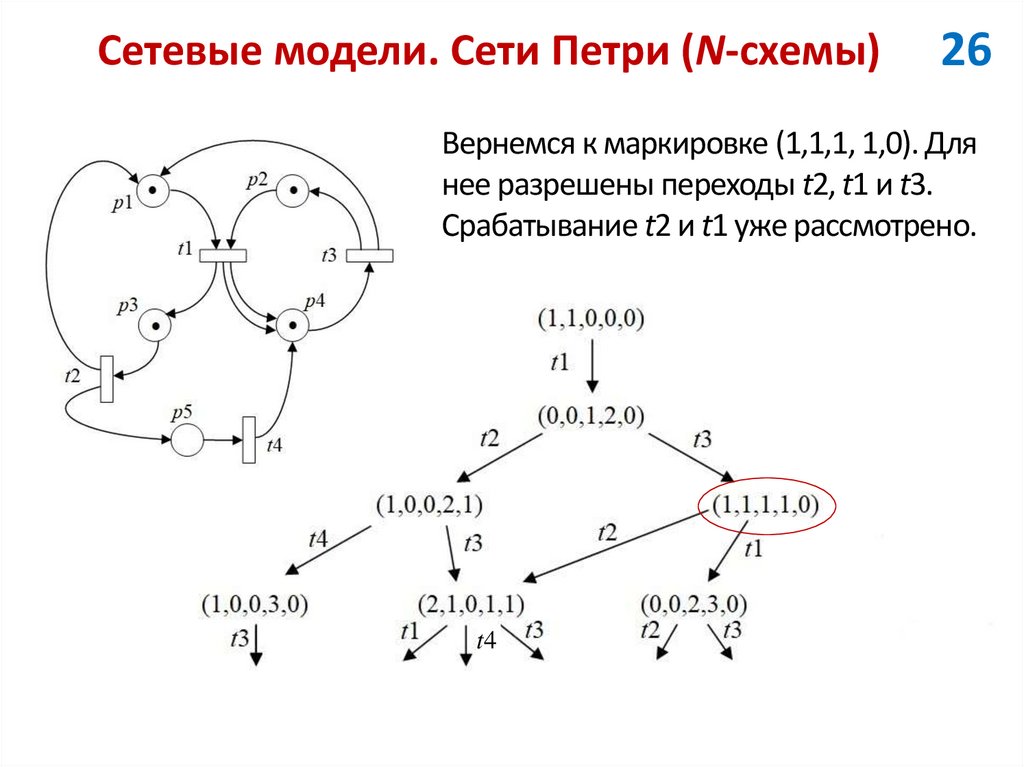
26
Вернемся к маркировке (1,1,1, 1,0). Для
нее разрешены переходы t2, t1 и t3.
Срабатывание t2 и t1 уже рассмотрено.
t4

27. Сетевые модели. Сети Петри (N-схемы)

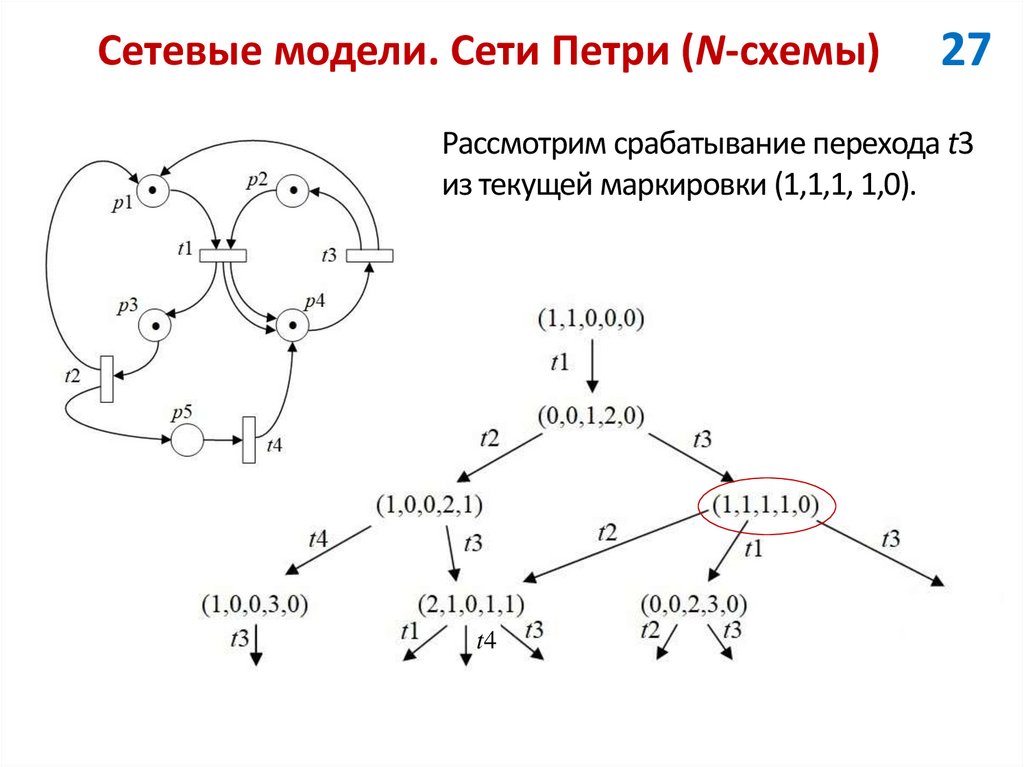
27
Рассмотрим срабатывание перехода t3
из текущей маркировки (1,1,1, 1,0).
t4

28. Сетевые модели. Сети Петри (N-схемы)

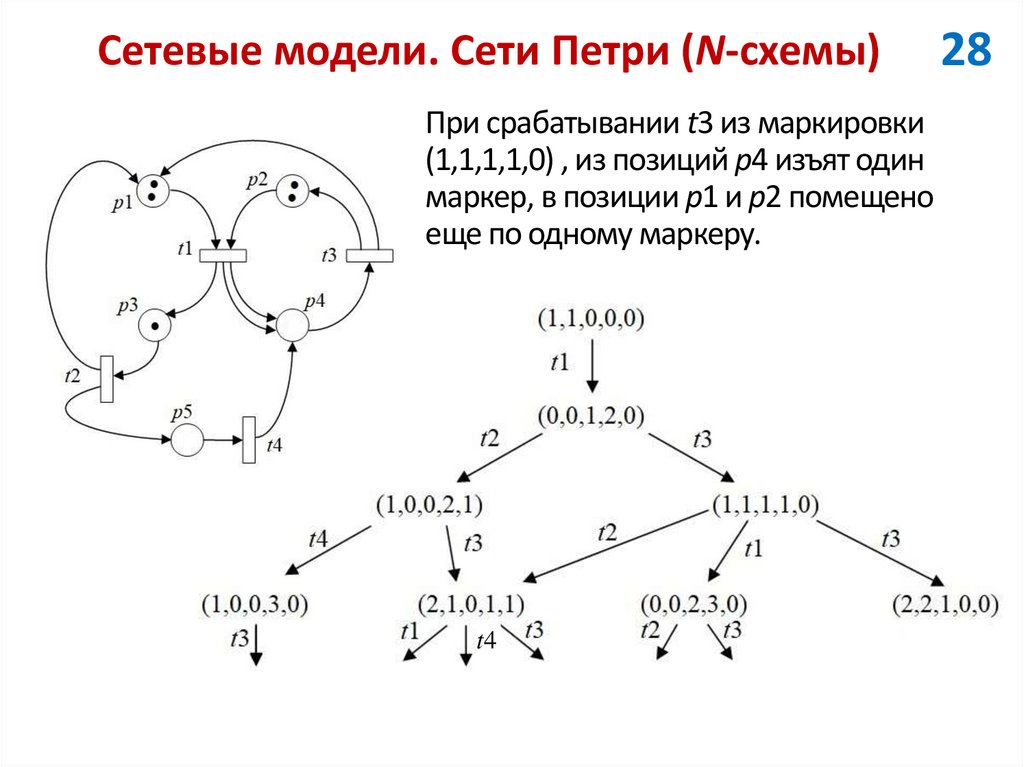
При срабатывании t3 из маркировки
(1,1,1,1,0) , из позиций p4 изъят один
маркер, в позиции p1 и p2 помещено
еще по одному маркеру.
t4
28

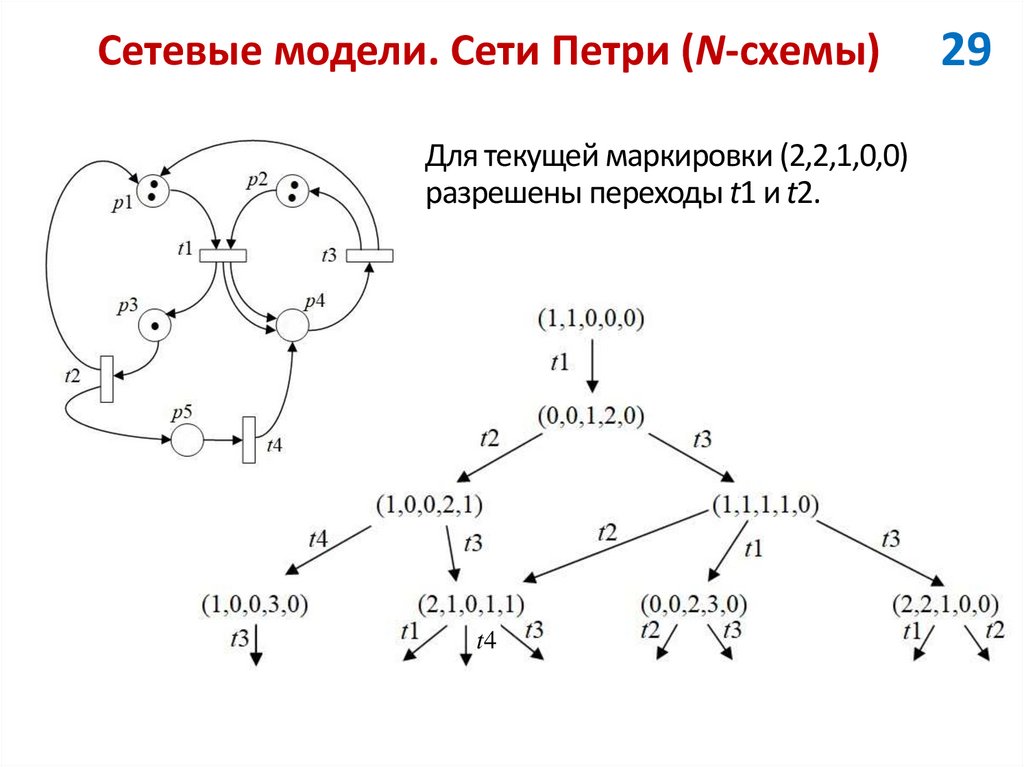
29. Сетевые модели. Сети Петри (N-схемы)

Для текущей маркировки (2,2,1,0,0)
разрешены переходы t1 и t2.
t4
29

30. Сетевые модели. Сети Петри (N-схемы)

30
Основными
свойствами
сетей
Петри
являются
ограниченность и безопасность, живость, сохраняемость.
Позиция рi сети Петри с начальной маркировкой µ(рi)
называется n-ограниченной, если число маркеров в ней не
может превышать целого числа n, или µ(рi) ≤ n, µ R(N).
Каждая позиция может иметь свое значение n. Сеть Петри
ограничена, если ограничены все ее позиции. Если n –
максимальное число маркеров, которое может быть в одной
позиции ограниченной сети Петри, то сеть называют n
ограниченной. Особый интерес представляют один
ограниченные позиции и сети, которые получили название
безопасных.

31. Сетевые модели. Сети Петри (N-схемы)

31
Сеть является живой, если,
во-первых, для каждого t T существуют i, j R(N) такие,
t
j ;
что i
во-вторых, для каждой пары i, j R(N) маркировка i
достижима из j.
Сеть Петри с начальной маркировкой µ называется строго
сохраняющей, если общее количество маркеров в процессе
выполнения сети остается постоянным. Строгое сохранение –
это очень сильное ограничение. Из него следует, что число
входов в каждый переход должно равняться числу выходов,
иначе запуск перехода изменил бы число маркеров в сети.

32. Сетевые модели. Сети Петри (N-схемы)

32
Сеть называется сохраняющей по отношению к весовому
вектору ,
=( 1, 2,… , n) , i 0, |P|=n,
если для каждой ’ R(N) выполняется условие
n
n
p = p
i 1
i
i
i 1
i
0
i
Строго сохраняющая сеть является сохраняющей по
отношению к вектору взвешивания = (1, 1, ..., 1).
Достижимость – анализ достижимости позволяет получить все
допустимые и недопустимые маркировки.

33. Сетевые модели. Сети Петри (N-схемы)

33
В зависимости от топологии выделяют следующие разновидности:
− автономная сеть, если для каждого перехода tj T имеется не
более одной входной и не более одной выходной позиции
( tj)=( tj )=1;
− маркированный граф, если для каждой позиции рi Р имеется
только 1 входной и один выходной переходы ( рi)=( рi )=1;
− сеть свободного выбора, если для каждого перехода tj T и для
каждой входной позиции рi ( tj), позиция рi является
единственной входной позицией перехода tj (если два перехода
имеют общую входную позицию, то эта позиция является
единственной для каждого из них);
− простая сеть, если любая пара переходов tj,tk T имеет не более
одной общей входной позиции;
− бесконфликтная сеть, в которой для каждой позиции рi Р
имеется не более одной исходящей дуги.

34. Сетевые модели. Сети Петри (N-схемы)

34
Модификацией классических сетей Петри являются временные
сети. Временная сеть позволяет в явном виде ввести в процесс
имитации время протекания отдельных действий, например,
транспортировка заготовок, загрузка-разгрузка станка, обработка
деталей на станке и т.д. Моделирование временными сетями
Петри применяют для различных целей:
− изучение процессов функционирования систем с целью оценки
их реализуемости;
− изучение проблем, связанных с ограниченностью общих
ресурсов для параллельно протекающих процессов;
− определение пропускной способности системы;
− определение узких мест;
− получение статистики по загрузке элементов системы.