1762063657787_4883

1. Функция, способы задания функции. Взаимно обратные функции. График функции. Область определения и множество значений функции.

Функция, способы задания функции.
Взаимно обратные функции. График
функции. Область определения
и множество значений функции. Нули
функции.
Подготовила:
Учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»
Рыбина М.В.

2. Определение

Функция - это соответствие между элементами
двух множеств, при котором каждому элементу x
из множества Х ставится в соответствие
единственный элемент y из множества Y.
Переменную
x
называют
независимой
переменной или аргументом функции.
Переменную
y
называют
зависимой
переменной.
Значения зависимой переменной называют
значениями функции.
Если зависимость переменной y от переменной
x является функцией, то коротко это записывают
так: y = f(x) (читают: «игрек равен эф от икс»).
Символ f(x) также обозначает значение
функции, соответствующее значению аргумента x.

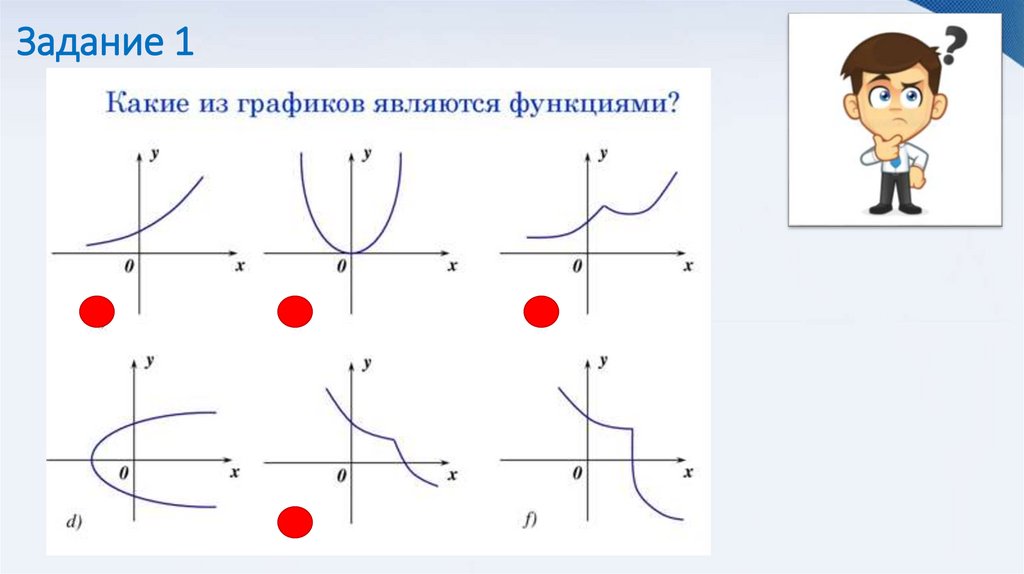
3. Задание 1

4.

5. Задание 2

Запишем область определения и
область значений функций

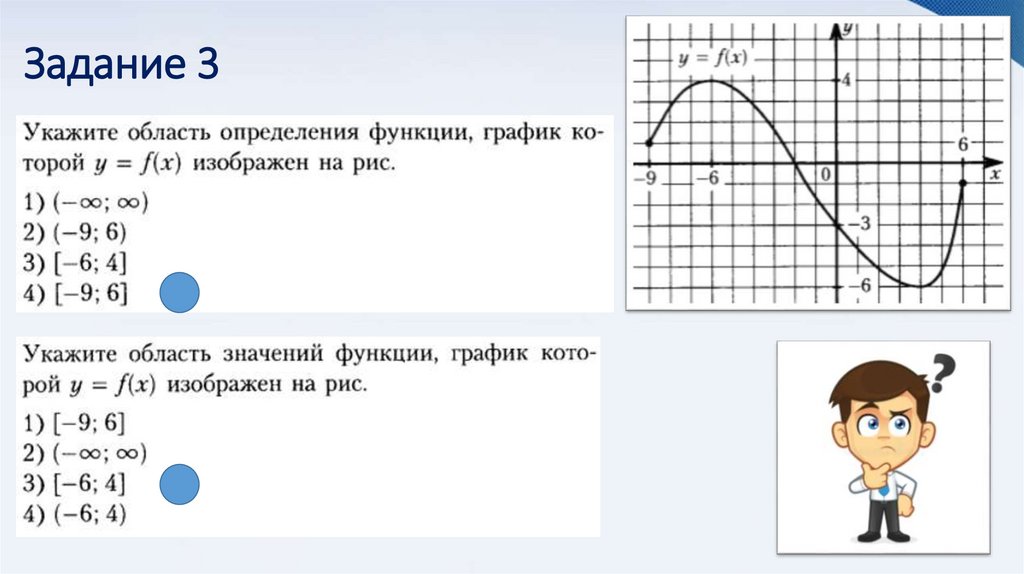
6. Задание 3

7. Задание 4

Найдите область определения функции:
2
а) у = ;
х
3
б) у =
;
х−2
2х
в) у =
;
х+5
4
г) у = 2 ;
х −1
2
д) у = 2 ;
х +5х
е) у = 2х − 5;
з) у =
3
;
5х −7
и) у = х − 3 +
1
5 −х

8.

9. Задание 5

Функция задана формулой у = -2х +7.
Найдите:
А) значения функции, если значения аргумента равны 3,5; - 4,5
Б) значения аргумента, если значения функции равны 5; - 4
Решение:
А) у = -2 3,5 +7 = 0
у = -2 (-4,5) + 7 = 16
Б) -2х +7 = 5
-2х +7= -4
-2х = 5 – 7
-2х = -4-7
-2х = -2
-2х = -11
х=1
х = 5,5

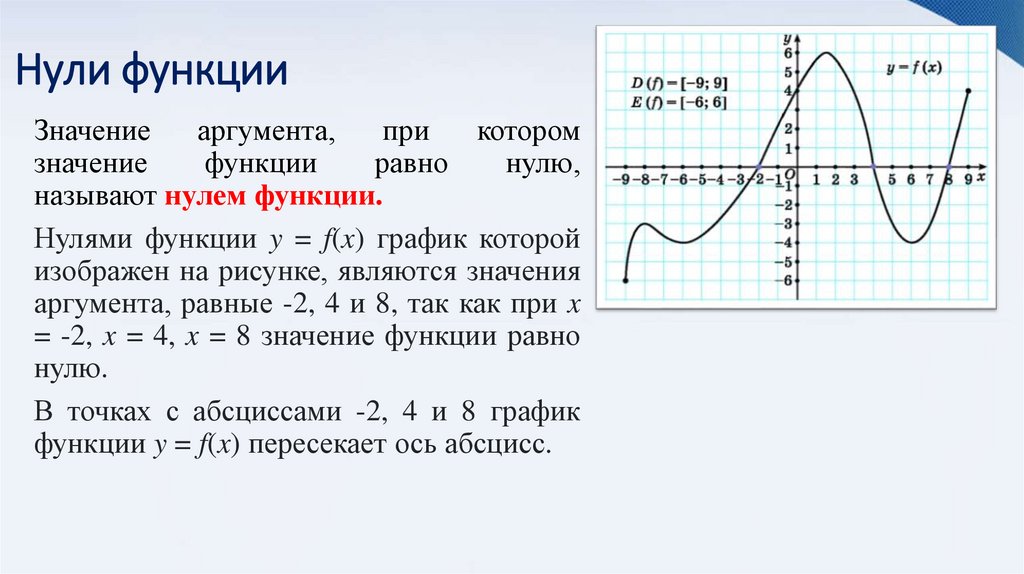
10. Нули функции

Значение
аргумента,
при
котором
значение
функции
равно
нулю,
называют нулем функции.
Нулями функции y = f(x) график которой
изображен на рисунке, являются значения
аргумента, равные -2, 4 и 8, так как при x
= -2, x = 4, x = 8 значение функции равно
нулю.
В точках с абсциссами -2, 4 и 8 график
функции y = f(x) пересекает ось абсцисс.

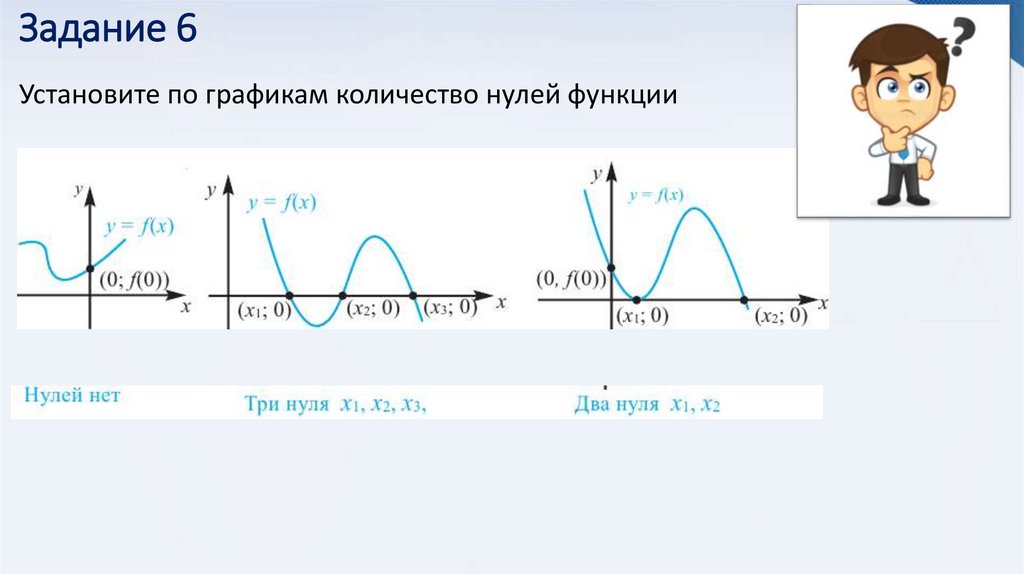
11. Задание 6

Установите по графикам количество нулей функции

12. Задание 7

Найдите нули функции

13. График функции

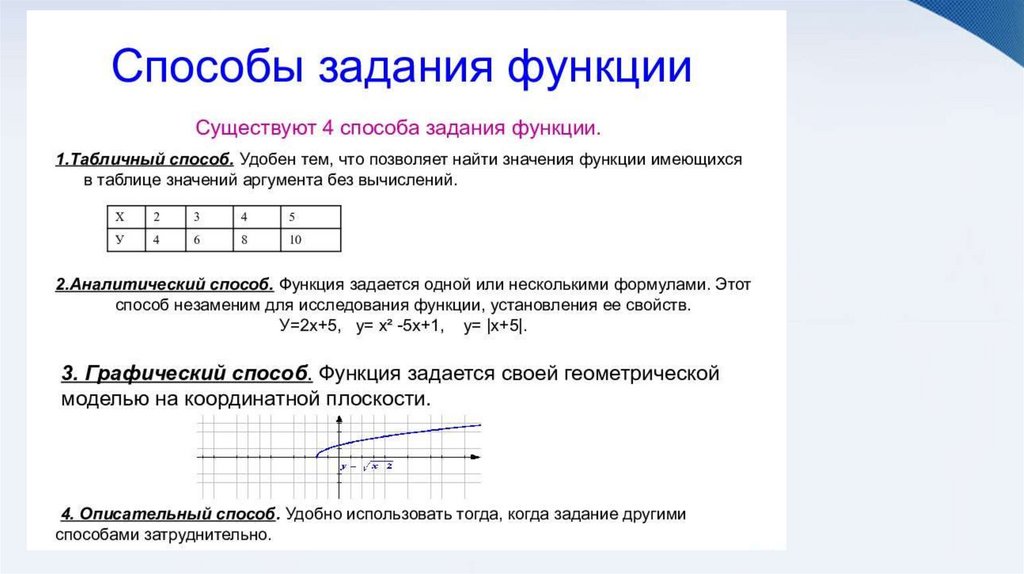
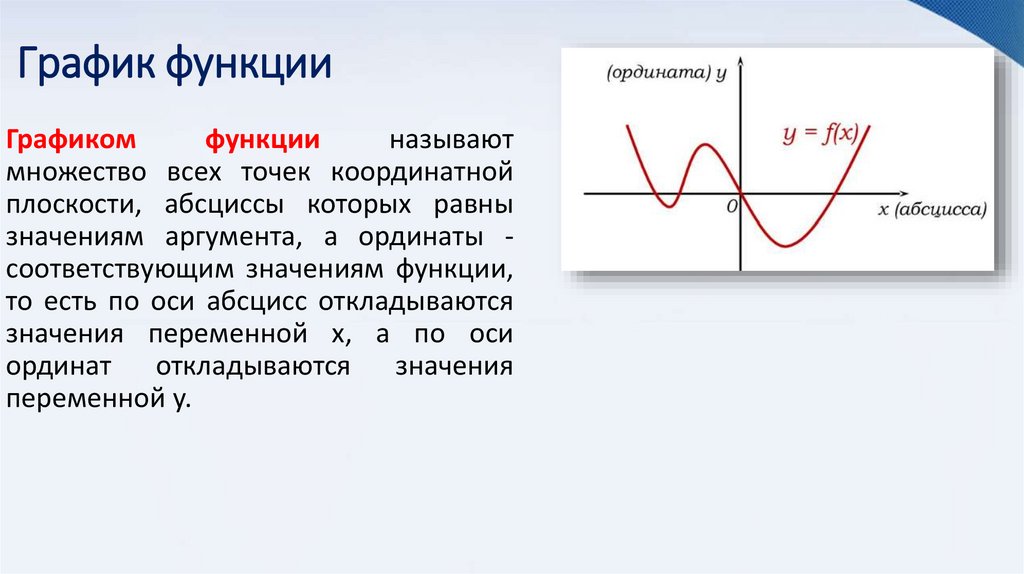
Графиком
функции
называют
множество всех точек координатной
плоскости, абсциссы которых равны
значениям аргумента, а ординаты соответствующим значениям функции,
то есть по оси абсцисс откладываются
значения переменной x, а по оси
ординат откладываются значения
переменной y.

14.

15.

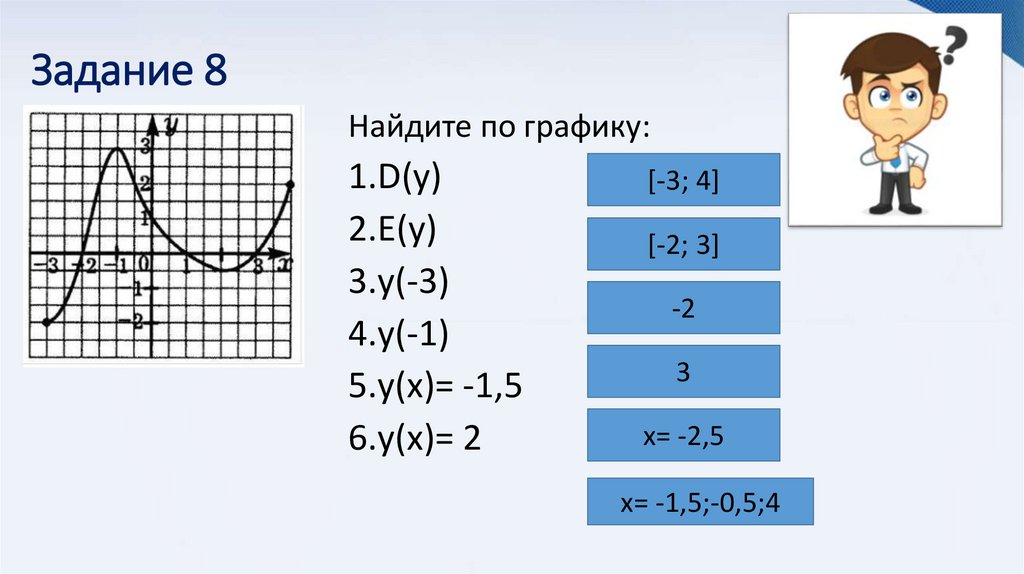
16. Задание 8

Найдите по графику:
1.D(y)
2.Е(y)
3.y(-3)
4.y(-1)
5.y(x)= -1,5
6.y(х)= 2
[-3; 4]
[-2; 3]
-2
3
x= -2,5
x= -1,5;-0,5;4

17. Взаимно обратные функции

Если функция y = f(x) принимает каждое свое значение только при
одном значении х, то эту функцию называют обратимой.
Например, функция y = 2x-2 обратима, так как каждое значение y
принимает при единственном значении х. Это значение можно найти,
решая уравнение y = 2x-2 относительно х.
y = 2x-2,
- 2x = - y – 2,
1
х = у + 1.
2
1
Теперь поменяем х и у местами: у = х + 1.
2
1
Функция у = х + 1 обратна к функции y = 2x-2
2

18. Алгоритм нахождения обратной функции

Если обратимая функция y = f(x) задана формулой, то для нахождения
обратной функции нужно
1. Решить уравнение f(x) = y относительно x.
2. Поменять местами x и у
3
Например: найдите функцию, обратную к функции у =
2х −5
3
3
3
2х – 5 = , 2х = + 5, х = + 2,5.
у
у
2у
3
Поменяем местами х и у: у = + 2,5
2х

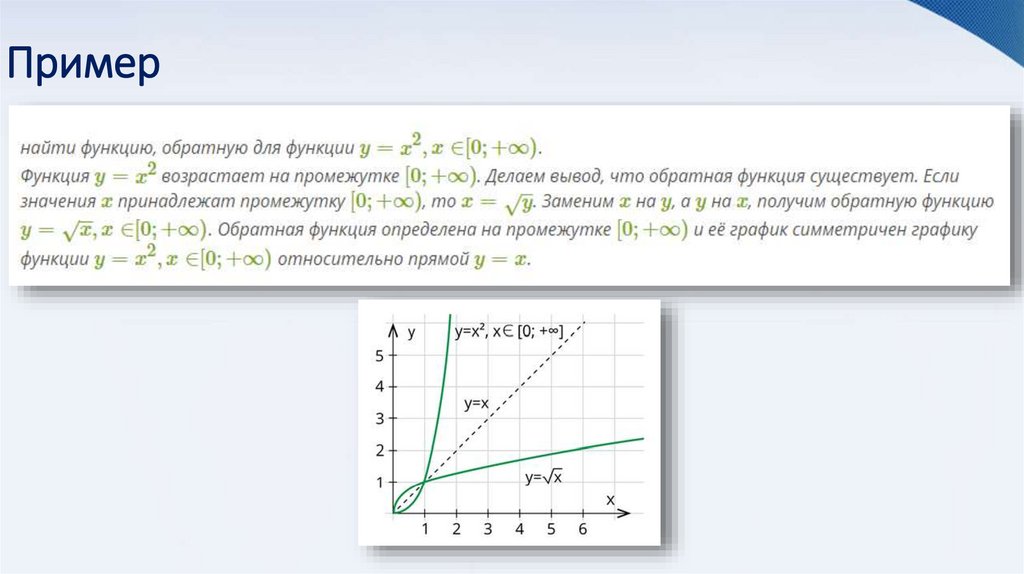
19. Пример

20. Задание 9

21. Задание 10

35
1

22. Задание 11

23. Домашнее задание

Читать § 7, стр.47
Выполнить в тетради № 132 (1,3,5), 134, 133 (6)

24. Использованные источники

https://resh.edu.ru/subject/lesson/5175/conspect/326684/
https://www.yaklass.ru/p/algebra/10-klass/chto-my-znaem-ochislovykh-funktciiakh-9133/obratimaia-i-obratnaia-funktcii-9159
https://lc.rt.ru/classbook/matematika-11-klass/podgotovka-kekzamenam/5290