Презентация_ЧФГ_Класс_моя

1.

Название команды
Класс
05.11.2025
Санкт-Петербург
(#)

2. Задача № 1. «Карманные деньги на лето»

Кирилл решил накопить к летним каникулам 9 000 ₽ на велосипед.
Каждую неделю родители дают ему 600 ₽, из которых он тратит 350 ₽, а
остальное кладёт в копилку.
У Кирилла скоро день рождения и родители обещали подарить ему по 1 000 ₽,
тётя 2 000 ₽, а бабушка и дедушка по 750 ₽.
Через 5 недель мама получила премию и дала сыну 500 ₽, так как увидела, что
Кирилл не потратит деньги.
Сможет ли Кирилл накопить нужную сумму за 10 недель, если будет
соблюдать план?

3. Задача № 1. «Карманные деньги на лето»

Решение:
600 – 350 = 250 ₽ - свободные деньги Кирилла
За 10 недель: 250 × 10 = 2 500 ₽
Подарки от родственников на день рождения:
1 000 × 2 + 2 000 + 750 × 2 = 5 500 ₽
Через 5 недель мама добавит 500 ₽
Итого:
2 500 + 5 500 + 500 = 8 500 ₽ сумма сбережений Кирилла
9 000 ₽ > 8 500 ₽
Ответ: Кирилл за 10 недель сможет накопить 8 500 ₽, что не достаточно для покупки велосипеда.

4. Задача № 2. «Семейный бюджет и рост цен»

Семья Петровых тратит 80 000 ₽ в месяц:
на продукты — 40%,
на коммунальные платежи — 25%,
на транспорт — 15%,
остальное — на прочие расходы.
Цены на продукты выросли на 20%, а на коммунальные услуги — на 10%.
Чтобы сохранить прежний уровень жизни, насколько процентов должна
вырасти зарплата Петровых?

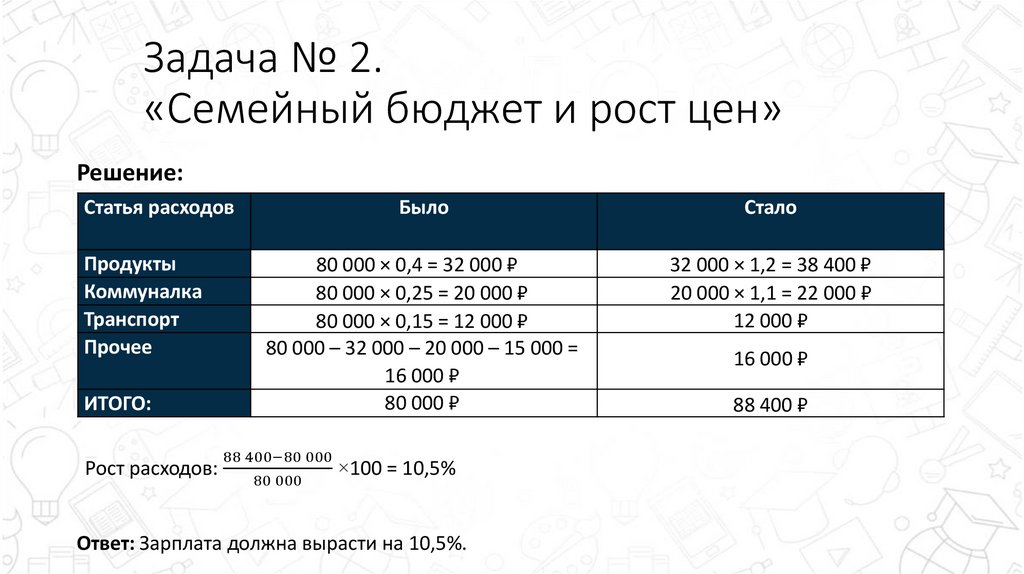
5. Задача № 2. «Семейный бюджет и рост цен»

Решение:
Статья расходов
Продукты
Коммуналка
Транспорт
Прочее
ИТОГО:
Рост расходов:
Было
Стало
80 000 × 0,4 = 32 000 ₽
80 000 × 0,25 = 20 000 ₽
80 000 × 0,15 = 12 000 ₽
80 000 – 32 000 – 20 000 – 15 000 =
16 000 ₽
80 000 ₽
32 000 × 1,2 = 38 400 ₽
20 000 × 1,1 = 22 000 ₽
12 000 ₽
88 400−80 000
×100 = 10,5%
80 000
Ответ: Зарплата должна вырасти на 10,5%.
16 000 ₽
88 400 ₽

6. Задача № 3. «Телефон или подписка?»

Аня хочет купить новый телефон.
Модель стоит 48 000 ₽, если оплатить сразу, можно получить скидку 5%.
Но магазин предлагает рассрочку на 6 месяцев без процентов при условии
покупки подписки на контент за 499 ₽ в месяц, первых 2 месяца бесплатно.
Как выгоднее поступить Ане, если она всё равно планировала оформлять
годовую подписку?

7. Задача № 3. «Телефон или подписка?»

Решение:
1. Покупка сразу:
2. Рассрочка:
48 000 × 0,95 = 45 600 ₽ - товар со скидкой 5%
48 000 + 499 × 10 = 48 000 + 4 990 = 52 990 ₽ -
Стоимость годовой подписки:
Стоимость товара с подпиской
499 × 12 = 5 988 ₽
45 600 + 5 988 = 51 588 ₽ - всего расходов
51 588 ₽ < 52 990 ₽
52 990 - 51 588 = 1 402 ₽ - разница
Ответ: Ане выгоднее покупку телефона оплатить сразу, экономия составит 1 402 ₽.

8. Задача № 4. «Когда выгоднее продать машину?»

Алексей купил новую машину за 1 200 000 ₽.
Каждый год её стоимость снижается на 20% (от текущей цены).
Если продать машину, вырученные деньги он может вложить в проект,
приносящий доход 30% в год.
Через сколько лет после покупки выгоднее продать машину, чтобы общий
финансовый результат был наибольшим?
(Считать, что вложенные средства и проценты не обесцениваются.)

9. Задача № 4. «Когда выгоднее продать машину?»

Решение:
1 Вариант:
Цена машины через 1 год дешевле на 20%:
1 200 000 × 0,8 = 960 000 ₽
Если Алексей продаст её, он может
заработать ещё 30% за год:
960 000 × 1,3 = 1 248 000 ₽ - сумма через 2 г.
1 248 000 × 1,3 = 1 622 400 ₽ - сумма через 3 г.
2 Вариант:
Цена машины через 1 год 960 000 ₽
Цена машины через 2 года дешевле на 20%:
960 000 × 0,8 = 768 000 ₽
Если Алексей продаст её, он может заработать
ещё 30% за год:
768 000 × 1,3 = 998 400 ₽ - сумма через 3 г.
Вывод: Через год машина стоит дороже 960 000 ₽, чем через два 768 000 ₽.
Если продать через 1 год, Алексей получит наибольшую выгоду 1 622 400 ₽, чем через 2 года 998 400 ₽.
Ответ: Алексею выгоднее продать автомобиль через 1 год — он получит максимальный
финансовый результат.

10. Задача № 5. «Подарок от банка»

Банк «Добрые деньги» предлагает вклад «Подарочный+» сроком на 1 год под 7,36 %
годовых.
Если вкладчик держит деньги весь год, то проценты начисляются на полную сумму.
Если снимает деньги раньше, то банк выплачивает половину начисленных процентов
за фактическое время хранения,
а если снимает раньше, чем через 6 месяцев, проценты не начисляются вообще.
Тимофей положил 20 000 ₽.
Через 9 месяцев он решил купить новый телефон и снял всю сумму.
Сколько рублей получил Тимофей от банка?

11. Задача № 5. «Подарок от банка»

Решение:
✅ 7,36 % годовых — это значит, что за 12 месяцев вкладчик получит 7,36 % от суммы размещения
✅ Нужно узнать, сколько процентов начислят за 9 месяцев,
а потом — половину, потому что Тимофей снял деньги раньше срока.
За год банк начислил бы:
20 000 × 7,36 : 100 = 1 472 ₽
9
За 9 месяцев — это года, значит:
12
1 472 ×
9
= 1 104 ₽
12
Так как Тимофей снял раньше срока, банк выплатит только половину процентов:
1 104 ÷ 2 = 552 ₽
Общая сумма:
20 000 + 552 = 20 552 ₽
Ответ: Тимофей по истечению 9 мес. получил от Банка 20 552 ₽.

12. Задача № 6. «Секретная надбавка пенсионерам»

Банк «Надёжный» предлагает вклад под 6% годовых.
Пенсионерам начисляется надбавка 25% от годового процента, но только на
тот период, когда они не снимают деньги.
Баба Катя положила 40 000 ₽ на 1 год.
Через 8 месяцев ей понадобились деньги на лечение, и она сняла половину
вклада (остальные деньги оставила на счёте до конца года).
Сколько рублей получила Баба Катя через год, если проценты начисляются в
конце года и пропорционально времени хранения?

13. Задача № 6. «Секретная надбавка пенсионерам»

Решение:
✅ 6% — это годовые, значит за 12 месяцев в Банке лежат деньги
✅ Для пенсионеров добавляется 25% к этим 6%
✅ Нужно учесть, что половина денег пролежала весь год, а половина — только 8 месяцев
Процентная ставка с надбавкой:
6% + 25% от 6% - это 6 × 1,25 = 7,5 % в год
Первые 8 месяцев на счёте было 40 000 ₽ :
8
40 000 × 0,075 × = 2 000 ₽
12
Всего процентов: 2 000 + 400 = 2 400 ₽
Оставшиеся 4 месяца (надбавка не действует):
Осталось 20 000 ₽, ставка = 6% годовых. :
4
20 000 × 0,06 × = 400 ₽
12
Что получила Баба Катя:
Через 8 мес. - 20 000 ₽
Через год 20 000 + 2 400 = 22 400 ₽
Итого: 20 000 + 22 400 = 42 400 ₽
Ответ: Через год баба Катя получит 42 400 ₽ - это сумма процентов.

14. Задача № 7. «Осторожный инвестор Коля»

Коля решил разделить свои 30 000 ₽:
половину он положил в банк “СейфБанк” под 8% годовых,
а вторую половину — в “КапиталБанк” под 7% годовых, но с ежемесячной
капитализацией процентов.
Что окажется выгоднее через год, и на сколько рублей больше принесёт этот
вариант?

15. Задача № 7. «Осторожный инвестор Коля»

Решение:
30 000 : 2 = 15 000 ₽ - в каждом банке
СейфБанк:
КапиталБанк:
15 000 × 0,08 = 1 200 ₽
7% годовых →
Через год: 15 000 + 1 200 = 16 200 ₽
Каждый месяц сумма немного растёт:
15 000 × (1 + 0,00583) ¹²
15 000 × 1,0725 = 16 087,5 ₽
7
≈ 0,583% в месяц
12
✅ Сравнение:
«СейфБан»: 16 200 ₽ > «КапиталБанк»: 16 087,5 ₽
16 200 – 16 087,5 = 112,5 ₽
Ответ: Для Коли более выгодный вариант размещения будет в «СейфБанк», доход выше на 112,5 ₽.

16. Задача № 7. «Осторожный инвестор Коля»

Решение:
30 000 : 2 = 15 000 ₽ - в каждом банке
СейфБанк:
КапиталБанк:
✅ Сравнение:
16 200 ₽ > 16 084 ₽
16 200 – 16 084 = 116 ₽
Ответ: Для Коли более выгодный вариант размещения будет в «СейфБанк», доход выше на 116 ₽.

17. Задача № 8. «Баба Зина и магия процентов»

Баба Зина внесла 50 000 ₽ на вклад в банке А под 2% годовых (проценты
выплачиваются в конце года, без промежуточной капитализации).
Через год на счёте банка А образовалась новая сумма. Баба Зина сняла ровно
половину этой суммы и перевела её в банк B, где годовая ставка в k раз выше, чем в
банке А (то есть ставка банка B равна 2k%). В банке B проценты также выплачиваются
в конце года. В банке А оставшаяся половина продолжила лежать на тех же условиях.
Ещё через год (то есть через два года от начала) общая сумма денег Бабы Зины на
двух счетах оказалась на 60% больше, чем её первоначальные 50 000 ₽.
Найдите годовую процентную ставку банка B.

18. Задача № 8. «Баба Зина и магия процентов»

Решение:
Начальная сумма: 50 000 ₽
Банк A: 2% годовых, проценты в конце года.
Через 1 год всю сумму в банке A стало: 50 000 ×1,02 = 51 000 ₽
Половину этой суммы перевели в банк B, половина осталась в банке A:
51 000 : 2 = 25 500 ₽ и там, и там.
Банк B: ставка в k раз выше, чем 2% → 2k% годовых (проценты в конце года).
Через ещё 1 год общая сумма на двух счетах стала на 60% больше исходной:
1,60 × 50 000 = 80 000 ₽

19. Задача № 8. «Баба Зина и магия процентов»

Модель через второй год
В банке A сумма через второй год:
25 500 × 1,02 = 26 010 ₽
В банке B сумма через второй год:
2к
25 500 × (1+ ) = 25 500 × (1+0,02k)
100
Складываем и приравниваем к 80 000 ₽:
26 010 + 25 500 × (1+0,02k) = 80 000 ₽
Вычислим k:
510k = 80 000 – 51 510
510 k = 28 490
K=
28 490
= 55,86
510
Тогда годовая ставка банка B:
2k% = 2 × 55,86 = 111,73 % годовых.
Раскроем скобки:
26 010 + 25 500 + 510k = 80 000 ₽
Ответ: Годовая ставка банка B 111,73 % годовых.

20. Задача № 8. «Баба Зина и магия процентов»

Решение:
1⃣ Начальная сумма: 50 000 ₽
Банк A: 2% годовых, проценты в конце года.
Через 1 год всю сумму в банке A стало: 50 000 ×1,02 = 51 000 ₽
2⃣ Половину этой суммы перевели в банк B, половина осталась в банке A:
51 000 : 2 = 25 500 ₽ и там, и там.
Через ещё 1 год общая сумма на двух счетах стала на 60% больше исходной:
1,60 × 50 000 = 80 000 ₽

21.

3⃣ Через второй год в банке А
Там 2% годовых, значит прибавится
25 500 × 0,02 = 510 ₽
Через год в банке А стало
25 500 + 510 = 26 010 ₽
4⃣ Через второй год в банке B
Там ставка — в несколько раз больше, и нам
нужно найти, сколько это процентов
Пусть ставка банка B —