графы дз

1. Модели на графах

2. Граф

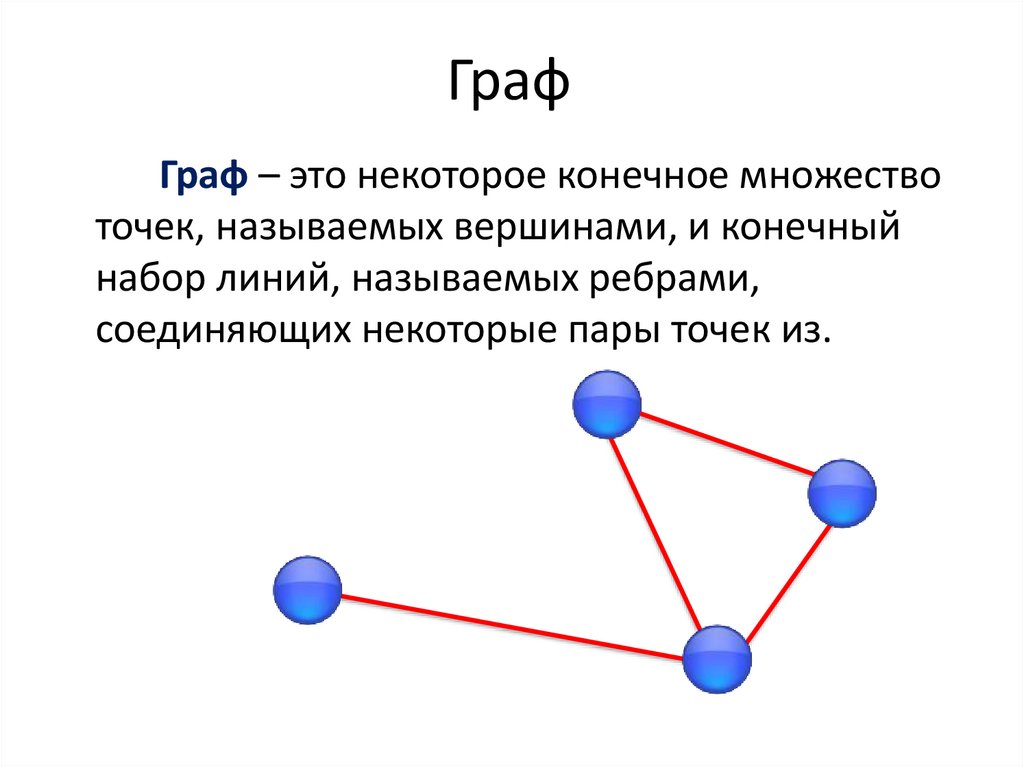
Граф – это некоторое конечное множество
точек, называемых вершинами, и конечный
набор линий, называемых ребрами,
соединяющих некоторые пары точек из.

3. Основные понятия графа

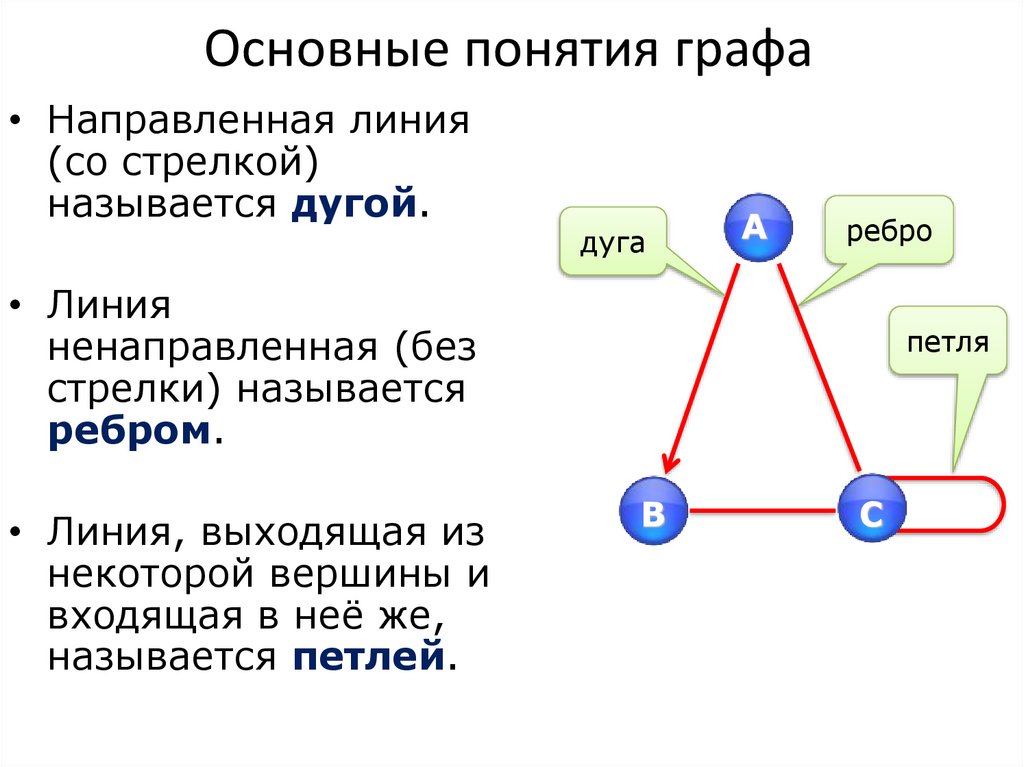
• Направленная линия
(со стрелкой)
называется дугой.
дуга
А
ребро
• Линия
ненаправленная (без
стрелки) называется
ребром.
• Линия, выходящая из
некоторой вершины и
входящая в неё же,
называется петлей.
петля
В
С

4. Виды графов

5. 1. Неориентированный граф

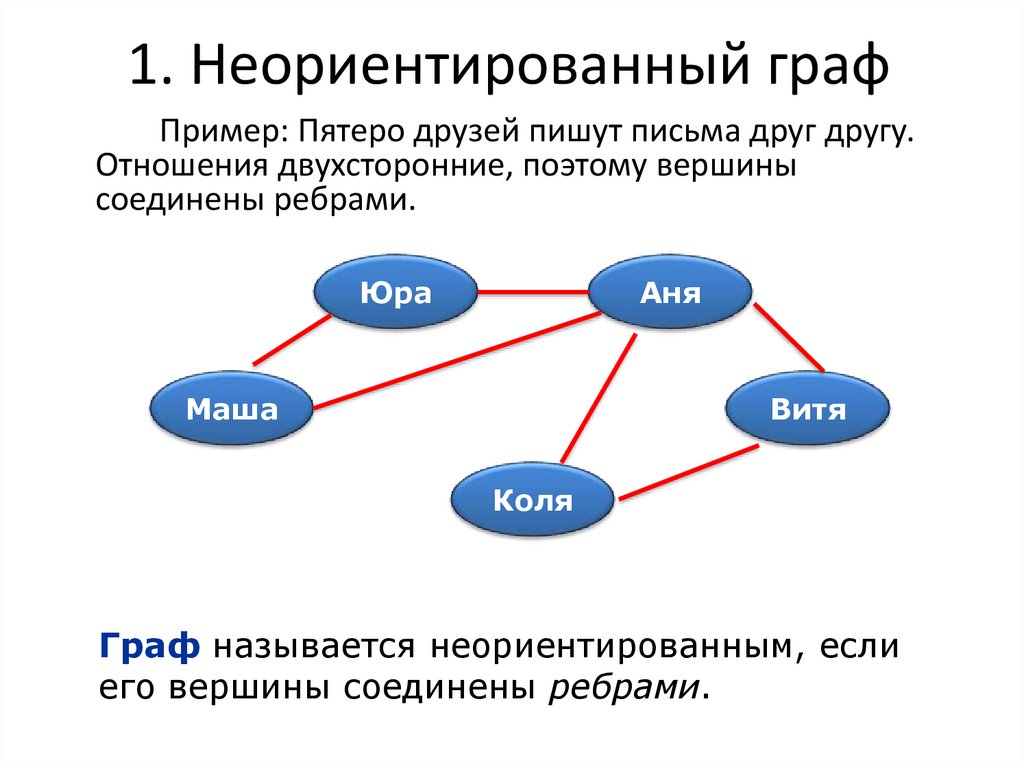
Пример: Пятеро друзей пишут письма друг другу.
Отношения двухсторонние, поэтому вершины
соединены ребрами.
Юра
Аня
Маша
Витя
Коля
Граф называется неориентированным, если
его вершины соединены ребрами.

6. Задача 1

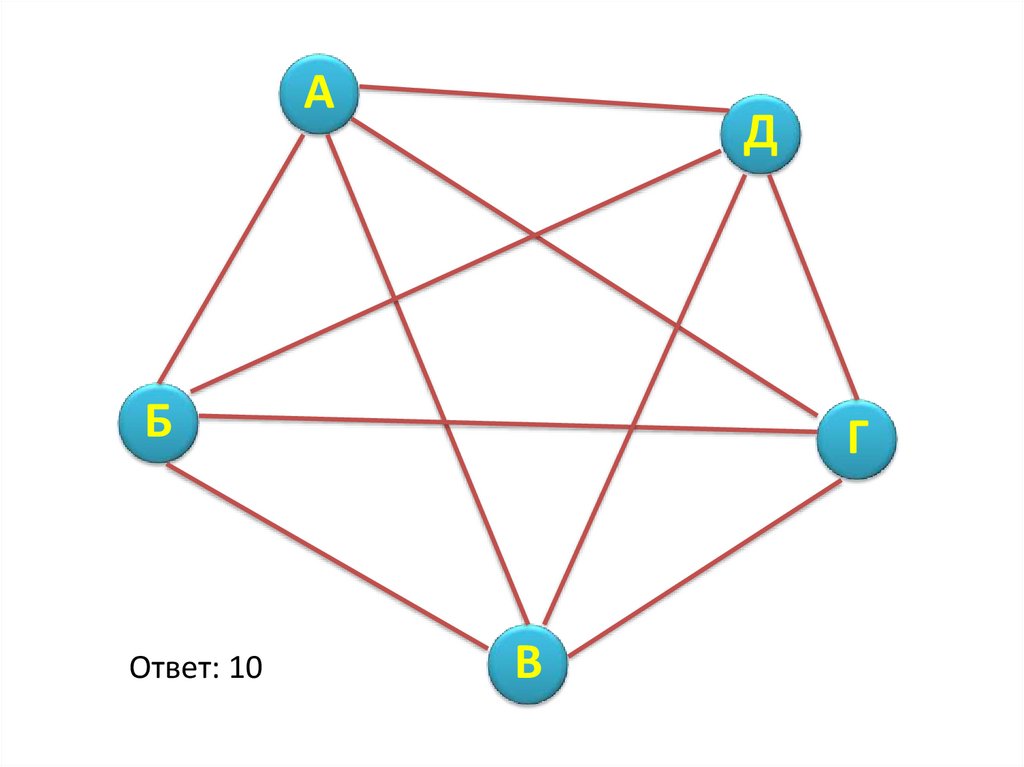
Аркадий, Борис, Владимир, Григорий и
Дмитрий при встрече обменялись
рукопожатиями (каждый пожал руку
каждому по одному разу). Сколько всего
рукопожатий было сделано?

7.

А
Д
Б
Ответ: 10
Г
В

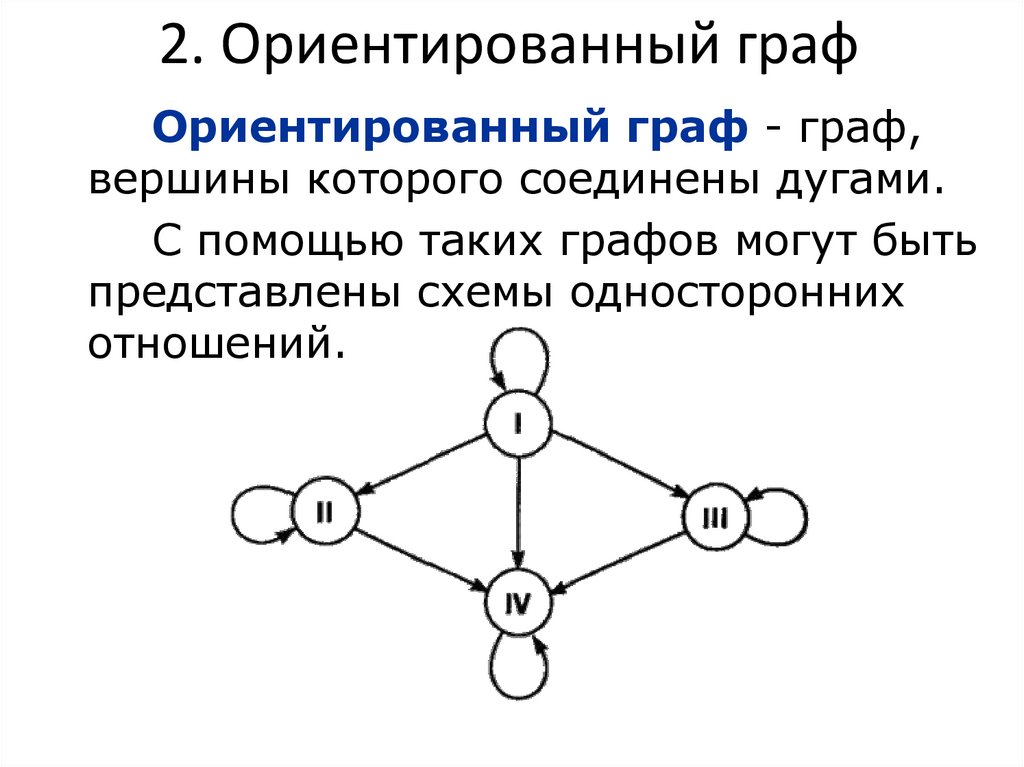
8. 2. Ориентированный граф

Ориентированный граф - граф,
вершины которого соединены дугами.
С помощью таких графов могут быть
представлены схемы односторонних
отношений.

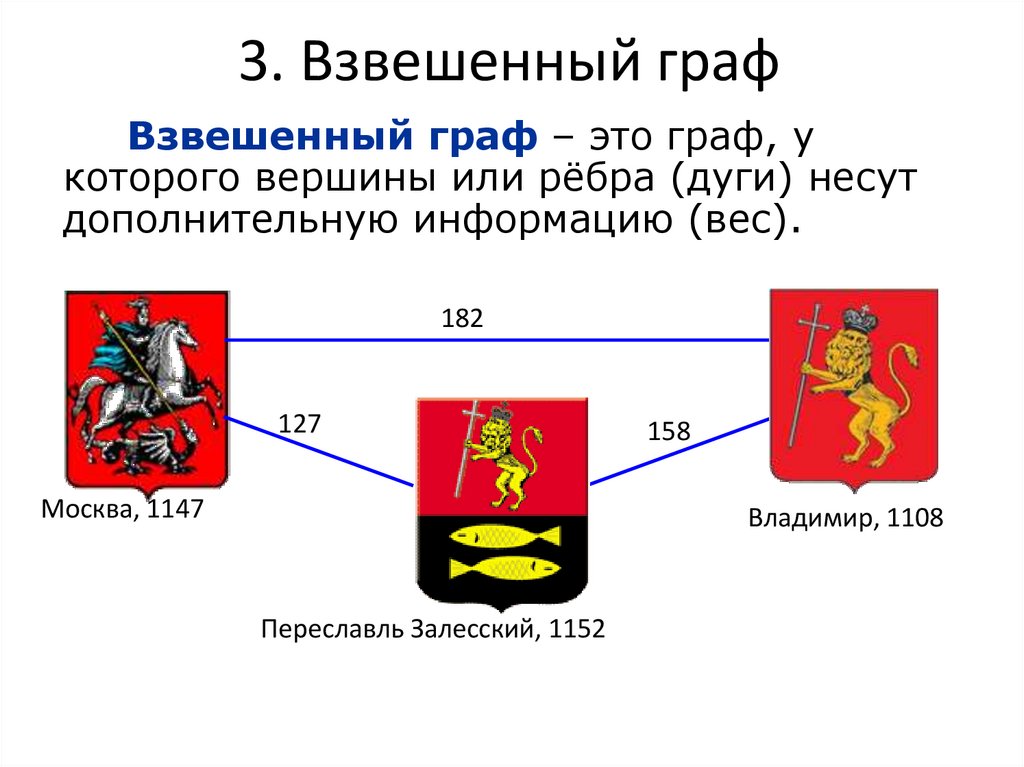
9. 3. Взвешенный граф

Взвешенный граф – это граф, у
которого вершины или рёбра (дуги) несут
дополнительную информацию (вес).
182
127
Москва, 1147
158
Владимир, 1108
Переславль Залесский, 1152

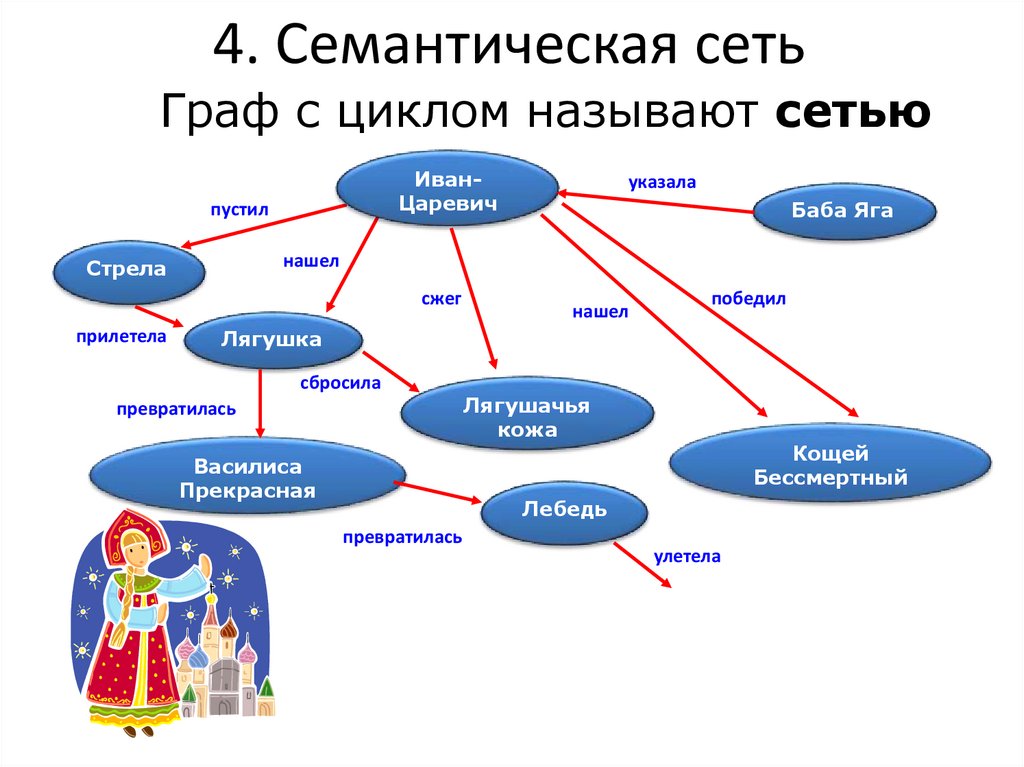
10. 4. Семантическая сеть

Граф с циклом называют сетью
ИванЦаревич
пустил
Баба Яга
нашел
Стрела
сжег
прилетела
указала
нашел
победил
Лягушка
сбросила
превратилась
Василиса
Прекрасная
Лягушачья
кожа
Кощей
Бессмертный
Лебедь
превратилась
улетела

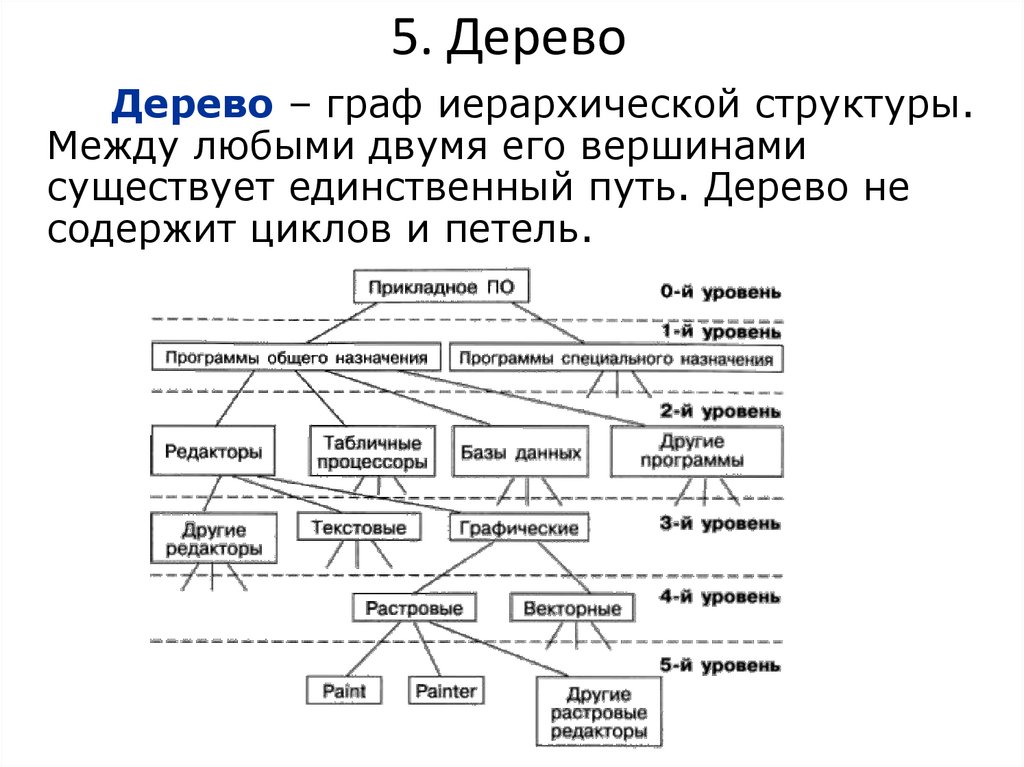
11. 5. Дерево

Дерево – граф иерархической структуры.
Между любыми двумя его вершинами
существует единственный путь. Дерево не
содержит циклов и петель.

12. Решение задач с помощью графов

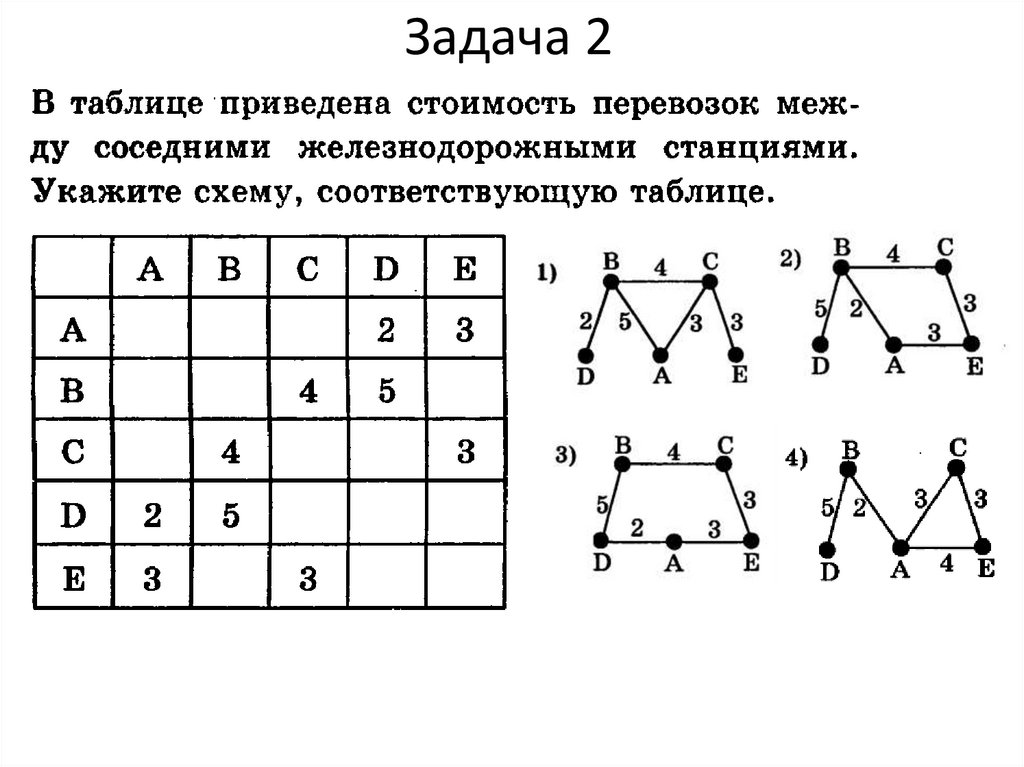
13. Задача 2

14.

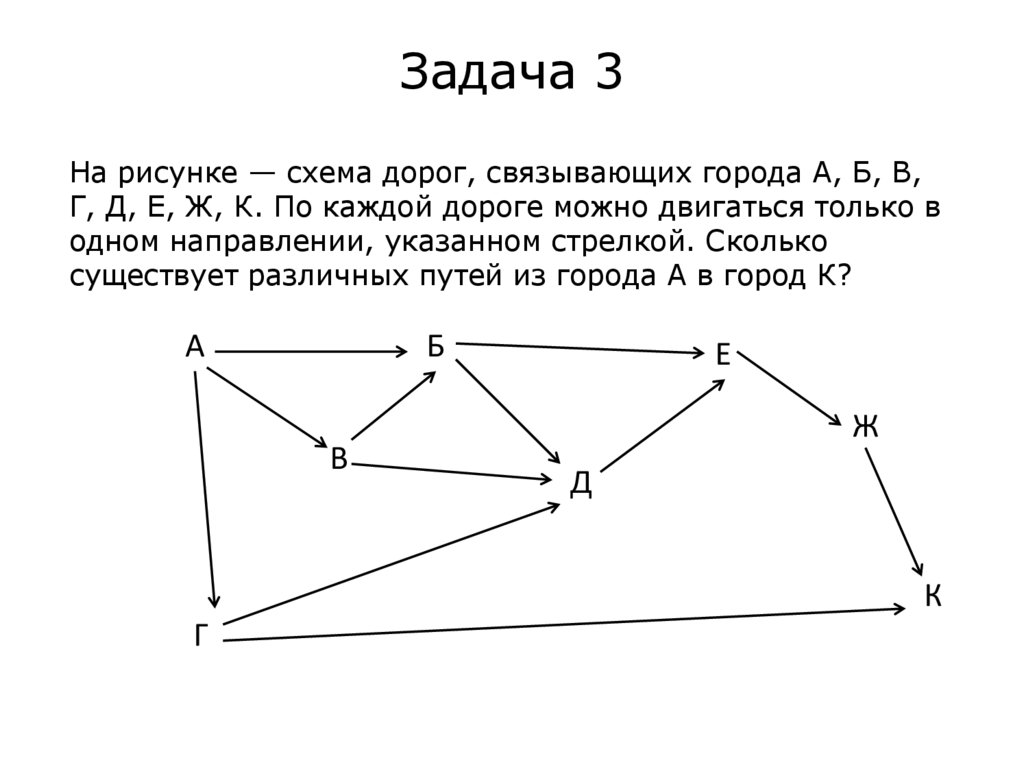
Задача 3
На рисунке — схема дорог, связывающих города А, Б, В,
Г, Д, Е, Ж, К. По каждой дороге можно двигаться только в
одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
А
Б
В
Е
Ж
Д
К
Г

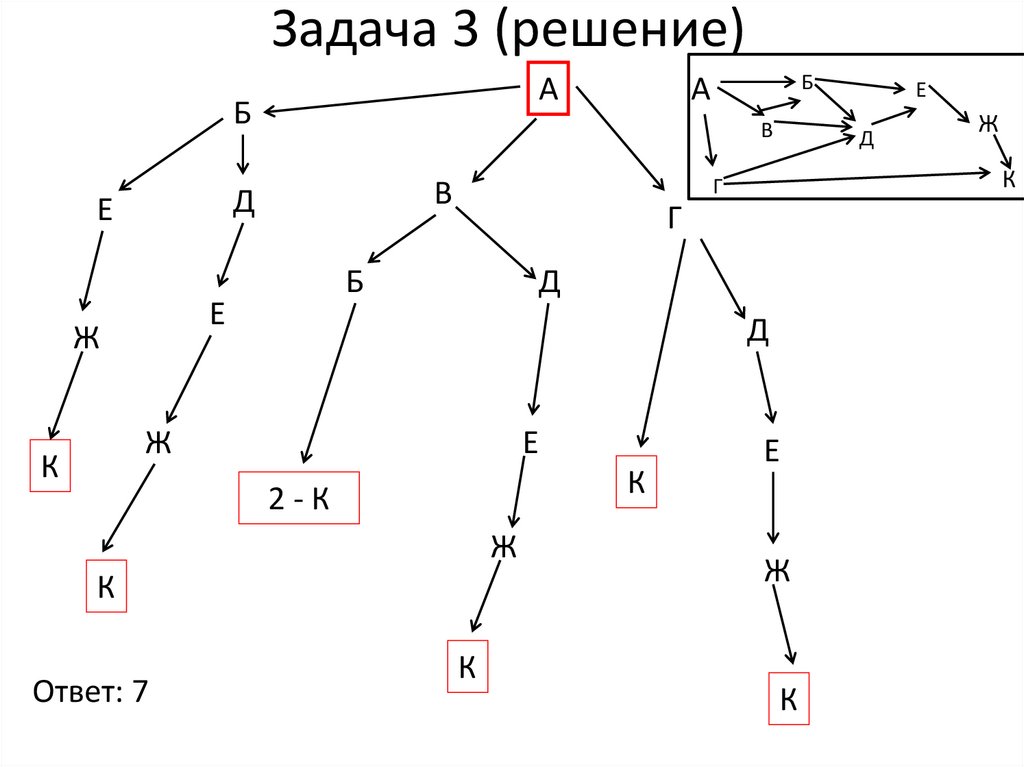
15. Задача 3 (решение)

А
Б
В
Е
Ж
Д
Д
Ж
К
Е
К
2-К
Ж
К
Ответ: 7
К
Ж
К
Г
Б
Е
Д
Г
В
Д
Е
Б
А
Е
Ж
К

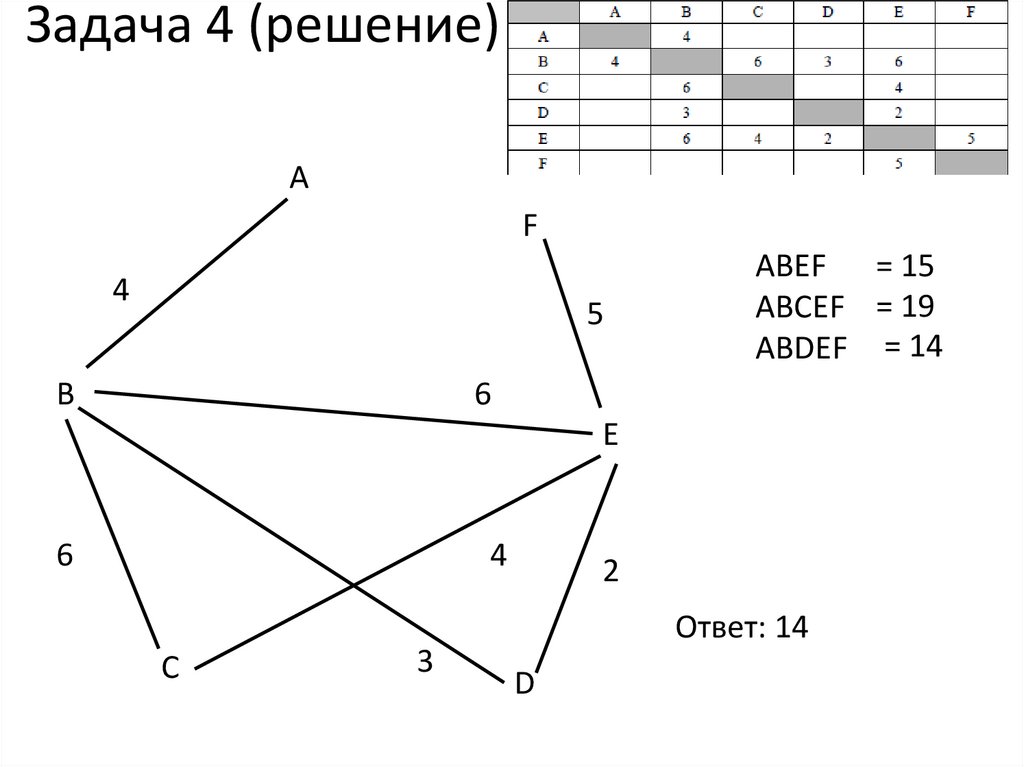
16. Задача 4

17. Задача 4 (решение)

А
F
4
5
В
ABEF = 15
ABCEF = 19
ABDEF = 14
6
E
6
4
С
3
2
Ответ: 14
D

18. Задача № 5

Для составления цепочек используются
бусины, помеченные буквами: А, В, С, D, Е.
На первом месте в цепочке стоит одна из
бусин А, С, Е. На втором — любая гласная,
если первая буква согласная, и любая
согласная, если первая гласная. На третьем
месте - одна из бусин С, D, Е, не стоящая в
цепочке на первом месте. Сколько цепочек
можно создать по этому правилу?

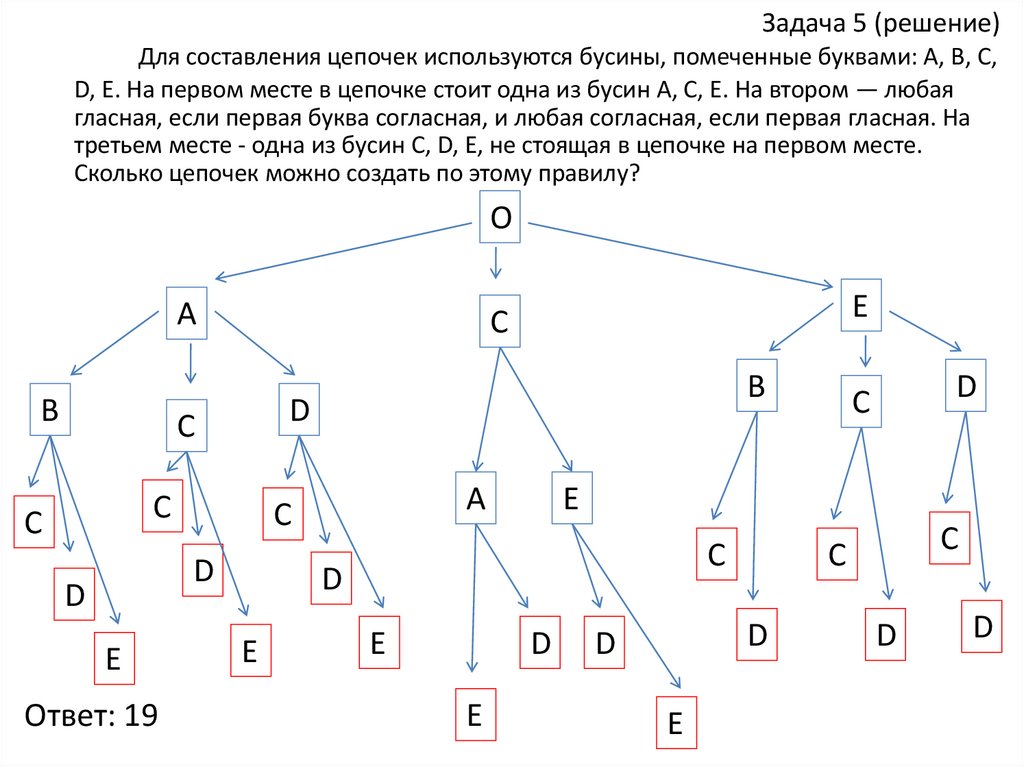
19. Задача 5 (решение)

Для составления цепочек используются бусины, помеченные буквами: А, В, С,
D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая
гласная, если первая буква согласная, и любая согласная, если первая гласная. На
третьем месте - одна из бусин С, D, Е, не стоящая в цепочке на первом месте.
Сколько цепочек можно создать по этому правилу?
О
А
B
C
E
Ответ: 19
А
C
D
D
B
D
C
C
E
C
E
C
D
E
E
D
E
D
C
D
D
E
C
C
D
D