Понятие множества. Операции над множествами.ppt

1.

Понятие множества.
Операции над
множествами
«Множество есть многое, мыслимое нами как единое»
(основатель теории множеств – Георг Кантор).

2. Понятия теории множеств

Понятие множества является одним из наиболее общих и
наиболее важных математических понятий. Оно было введено
в математику немецким ученым Георгом Кантором
(1845-1918). Следуя Кантору, понятие "множество" можно
определить так:
Множество – совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.

3.

Объекты, составляющие множество, называются элементами
множества.
Среди множеств выделяют особое множество - пустое множество.
Пустое множество - множество, не содержащее ни одного
элемента.
Пустое множество является частью любого множества.
Примеры пустых множеств.
1) Множество квадратных уравнений, которые имеют более двух разных
корней;
2) множество простых делителей числа 1;
3) множество точек пересечения двух параллельных прямых;
4) множество прямых углов равностороннего треугольника;
5) множество людей на Солнце;
6) множество двузначных положительных чисел, расположенных на числовом
луче левее 9.

4. Пустое множество

5.

Множество считается определенным , если указаны
все его элементы. Эти элементы могут быть указаны с
помощью некоторого общего признака или с помощью
некоторого списка, где обозначены все элементы.
Конечное множество- множество, состоящее из
конечного числа элементов.
Бесконечное множество- непустое множество, не
являющееся конечным.

6.

Пример: Множество натуральных чисел является
бесконечным.
Упорядоченное множество – множество, каждому элементу
которого поставлено в соответствие некоторое число (номер
этого элемента) от 1 до n, где n – число элементов
множества, так что различным элементам соответствуют
различные числа.
Каждое конечное множество можно сделать упорядоченным,
если, например, переписать все элементы в некоторый
список (a, b, c, d,...), а затем поставить в соответствие
каждому элементу номер места, на котором он стоит в
списке.

7. Способы задания множеств

Перечислением элементов множества;
Описанием общего (характеристического)
свойства, объединяющего элементы.
Приведите примеры множеств. Используя способы их
задания.

8.

№1
Какое множество задано
путем
перечисления
его
элементов?
А={0,1,2,3,4,5,6,7,8,9}

9.

№2
Задайте
множество лошадей,
пасущихся, на Луне.

10.

Пример:
1 Множество учеников данного класса определяется их
списком в классном журнале
2 множество всех стран на земном шаре – их списком в
атласе
3 множество всех костей в человеческом теле - их списком в
учебнике анатомии
4 Хотя множество всех рыб в океане конечно, вряд ли его
можно задать списком
5 Свойство "быть квадратом целого числа" задает
(бесконечное) множество всех квадратов целых чисел
6 Множество толстокожих животных, имеющих два бивня,
совпадает со множеством толстокожих животных,
имеющих хобот, - это множество слонов

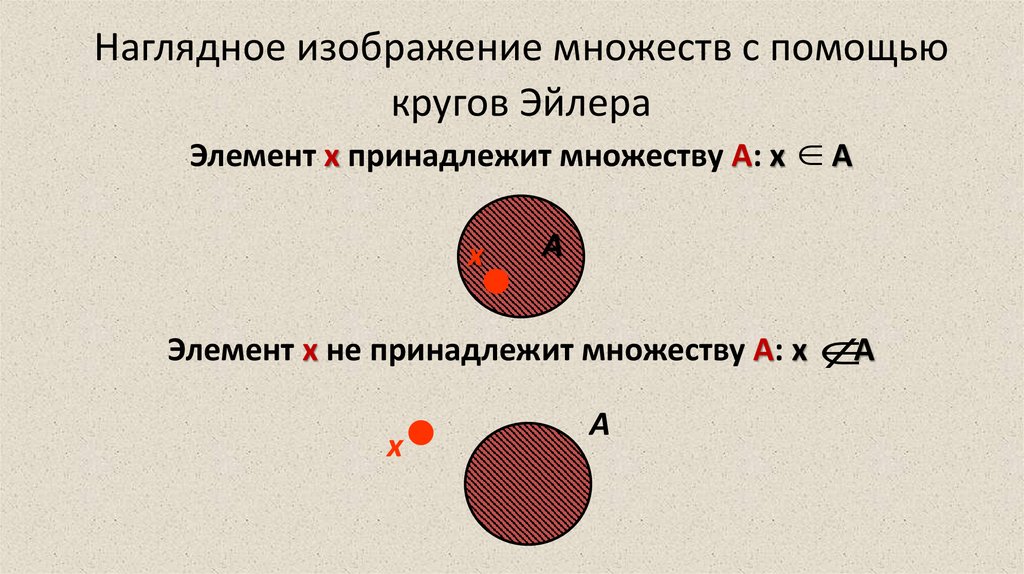
11. Наглядное изображение множеств с помощью кругов Эйлера

Элемент х принадлежит множеству А: х А
х
А
Элемент х не принадлежит множеству А: x А
х
А

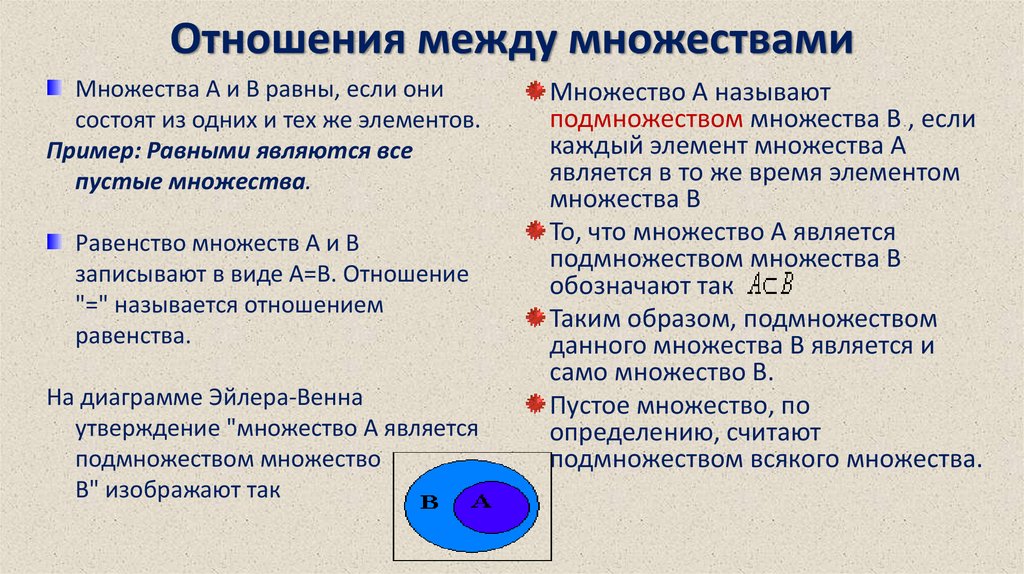
12. Отношения между множествами

Множества А и В равны, если они
состоят из одних и тех же элементов.
Пример: Равными являются все
пустые множества.
Равенство множеств А и В
записывают в виде А=В. Отношение
"=" называется отношением
равенства.
На диаграмме Эйлера-Венна
утверждение "множество А является
подмножеством множество
В" изображают так
Множество А называют
подмножеством множества В , если
каждый элемент множества А
является в то же время элементом
множества В
То, что множество А является
подмножеством множества В
обозначают так
Таким образом, подмножеством
данного множества В является и
само множество В.
Пустое множество, по
определению, считают
подмножеством всякого множества.

13. Мощность множеств

• Множества А и В имеют равные (одинаковые) мощности, если между
элементами этих множеств можно установить взаимно-однозначное
соответствие.
Пример:
А={1,2, 3} и В = {2,4,9.}
Можно установить взаимно-однозначное соответствие
Эти множества имеют равные мощности.
1, 2, 3.
1, 4, 9.
Если А и В – конечные множества, А состоит из n₁ элементов, а В состоит из n2
элементов, то мощности А и В равны, если n1 = n2
Мощность А меньше мощности В, если n₁ < n2 .
Мощность конечного множества А меньше мощности бесконечного В.

14.

А В

15.

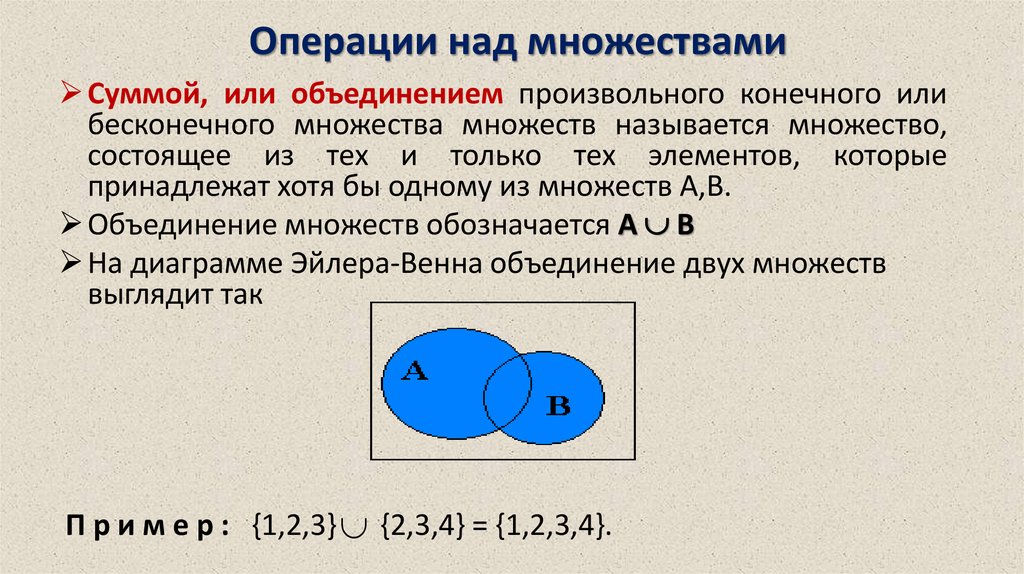
Операции над множествами
Суммой, или объединением произвольного конечного или
бесконечного множества множеств называется множество,
состоящее из тех и только тех элементов, которые
принадлежат хотя бы одному из множеств А,В.
Объединение множеств обозначается А В
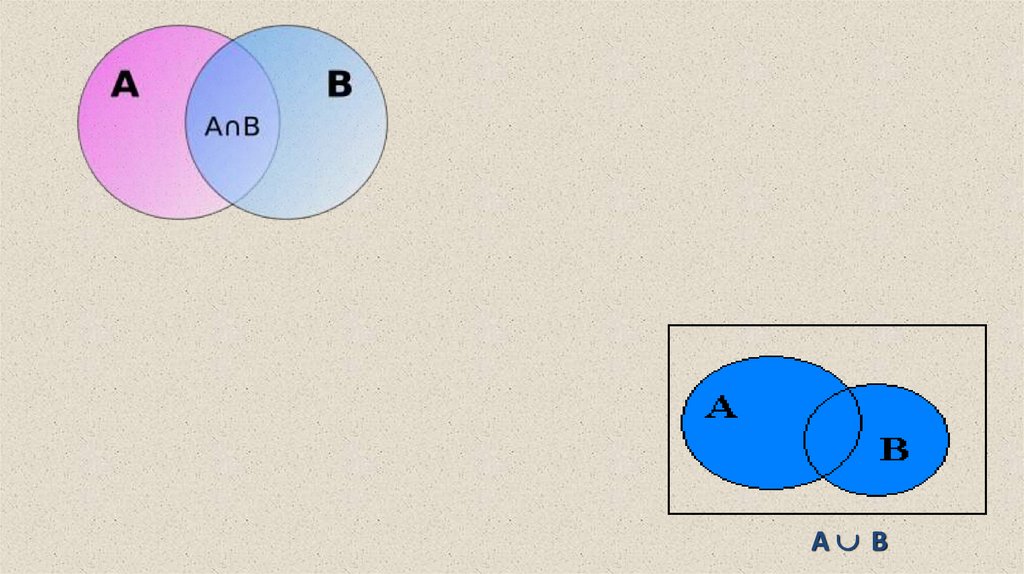
На диаграмме Эйлера-Венна объединение двух множеств
выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.

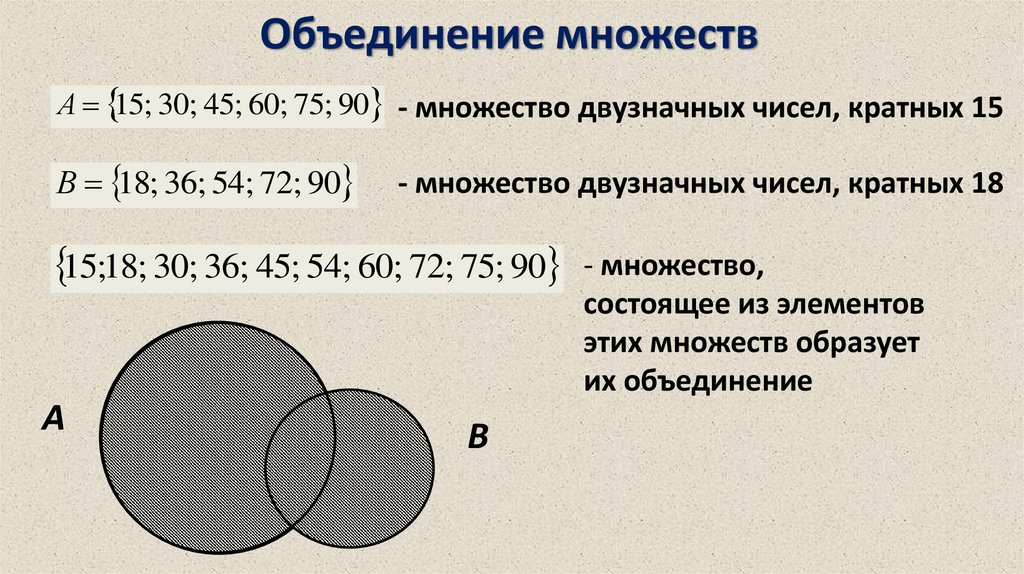
16. Объединение множеств

А 15; 30; 45; 60; 75; 90 - множество двузначных чисел, кратных 15
В 18; 36; 54; 72; 90
- множество двузначных чисел, кратных 18
15;18; 30; 36; 45; 54; 60; 72; 75; 90 - множество,
состоящее из элементов
этих множеств образует
их объединение
А
В

17.

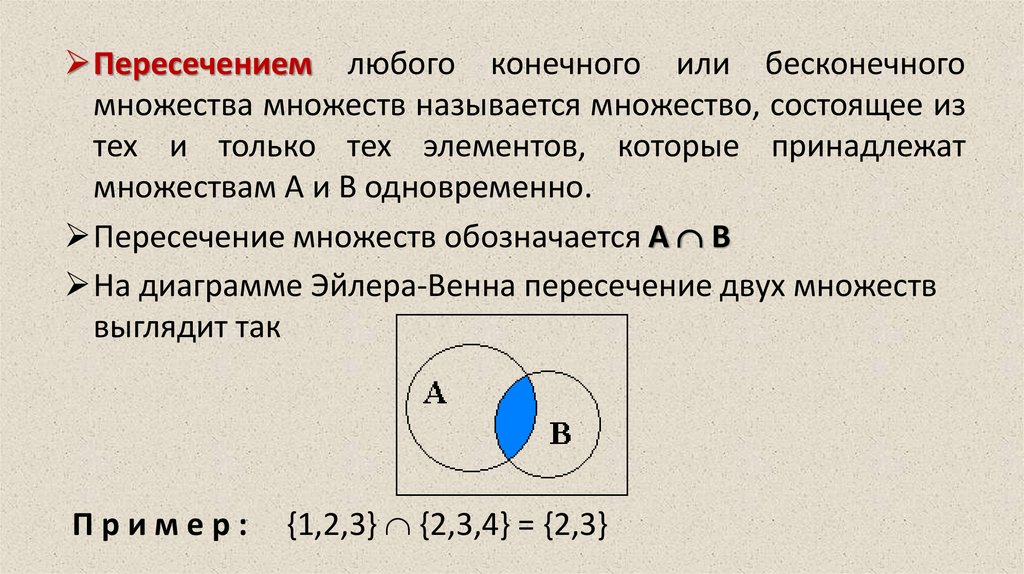
Пересечением любого конечного или бесконечного
множества множеств называется множество, состоящее из
тех и только тех элементов, которые принадлежат
множествам А и В одновременно.
Пересечение множеств обозначается А В
На диаграмме Эйлера-Венна пересечение двух множеств
выглядит так
Пример:
{1,2,3} {2,3,4} = {2,3}

18. Пересечение множеств

А а; б; с; д; е; ф
- танцевальная группа класса
В а; б; с; м; т; у - хоровая группа класса
а; б; с - члены обеих групп образуют
пересечение множеств А и В
А В
В
А

19.

Даны множества
А = {3,5, 0, 11, 12, 19},
В = {2,4, 8, 12, 18,0}.
Найдите множества A В, А В

20.

В классе 30 человек, каждый из
которых
поёт
или
танцует.
Известно, что поют 17 человек, а
танцевать умеют 19 человек.
Сколько человек поёт и танцует
одновременно?

21. Решение

Пусть А – это множество учеников, умеющих петь. Количество
элементов в нём по условию равно n = 17. Пусть В –
множество учеников, умеющих танцевать. Количество
элементов в нём – m = 19.
А В – множество совпадает со всем классом, т.к. каждый
ученик в классе поёт или танцует.
А В – это множество тех учеников класса, которые поют и
танцуют одновременно.
(17 + 19) – 30 = 6
Ответ: 6 учеников в классе поют и танцуют одновременно.

22. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27

учащихся, а два языка — 18 учащихся. Сколько
учащихся в классе?
Решение:
Пусть А – множество учащихся изучающих
английский язык,
Ф – множество учащихся изучающих французский
язык,
О – множество учащихся изучающих английский и
французский язык.
25 - 18=7 (уч.) – изучают только английский;
27 - 18=9 (уч.) – изучают только французский;
3)18 + (7 + 9) = 34(уч.)
Ответ: в классе 34 ученика.