Лаб1

1. Методы нулевого порядка при поиске экстремума функции одной переменной

МЕТОДЫ НУЛЕВОГО ПОРЯДКА
ПРИ ПОИСКЕ ЭКСТРЕМУМА ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ

2. Методы безусловной минимизации функций одной переменной

МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
2

3. Прямые методы одномерного поиска

ПРЯМЫЕ МЕТОДЫ ОДНОМЕРНОГО ПОИСКА
Поскольку задачи максимизации и минимизации легко
преобразуются одна в другую, то в дальнейшем будем
рассматривать только задачи минимизации.
Минимизировать функцию одной переменной f(x)
при условии a x b , то есть найти x * a, b
такую что f ( x * ) f ( x) для x a, b .
Интервал a, b называется интервалом неопределенности; функция f (x) называется минимизирующей
или целевой функцией.
3

4. Методы исключения отрезков

МЕТОДЫ ИСКЛЮЧЕНИЯ ОТРЕЗКОВ

5.

МЕТОДЫ ИСКЛЮЧЕНИЯ ОТРЕЗКОВ
Метод половинного
деления
Метод «золотого»
сечения
Метод Фибоначчи

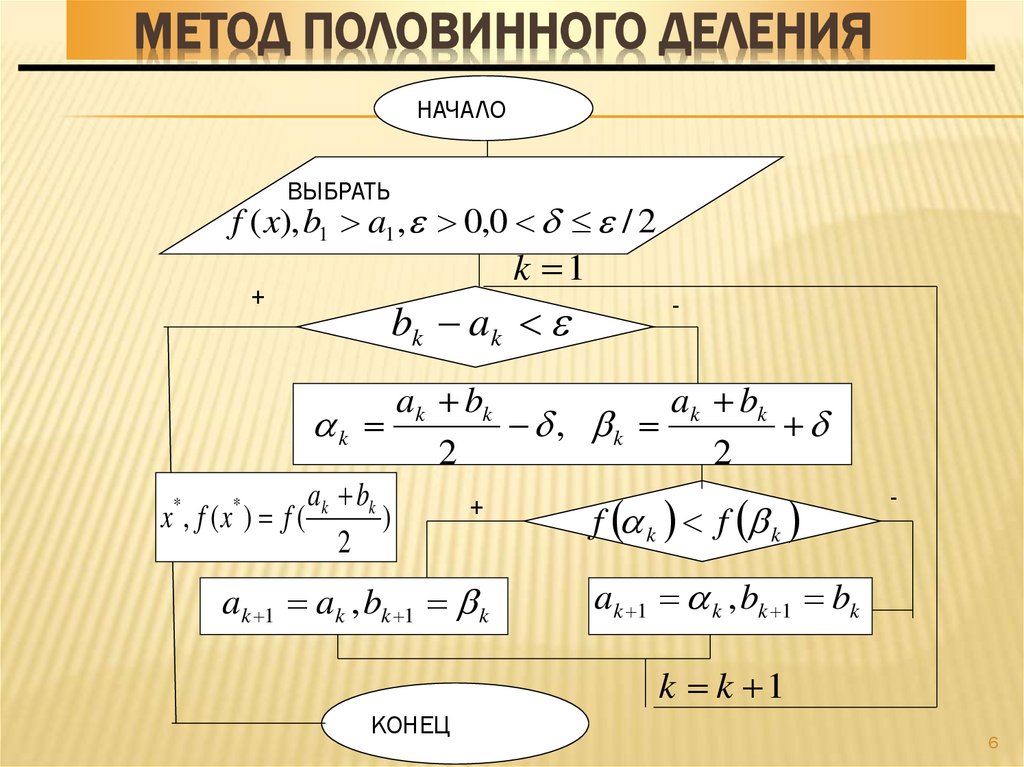
6. Метод половинного деления

МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
НАЧАЛО
ВЫБРАТЬ
f ( x), b1 a1 , 0,0 / 2
k 1
+
bk ak
-
ak bk
ak bk
k
, k
2
2
ak bk
x , f (x ) f (
)
2
*
*
+
ak 1 ak , bk 1 k
f k f k
-
ak 1 k , bk 1 bk
k k 1
КОНЕЦ
6

7.

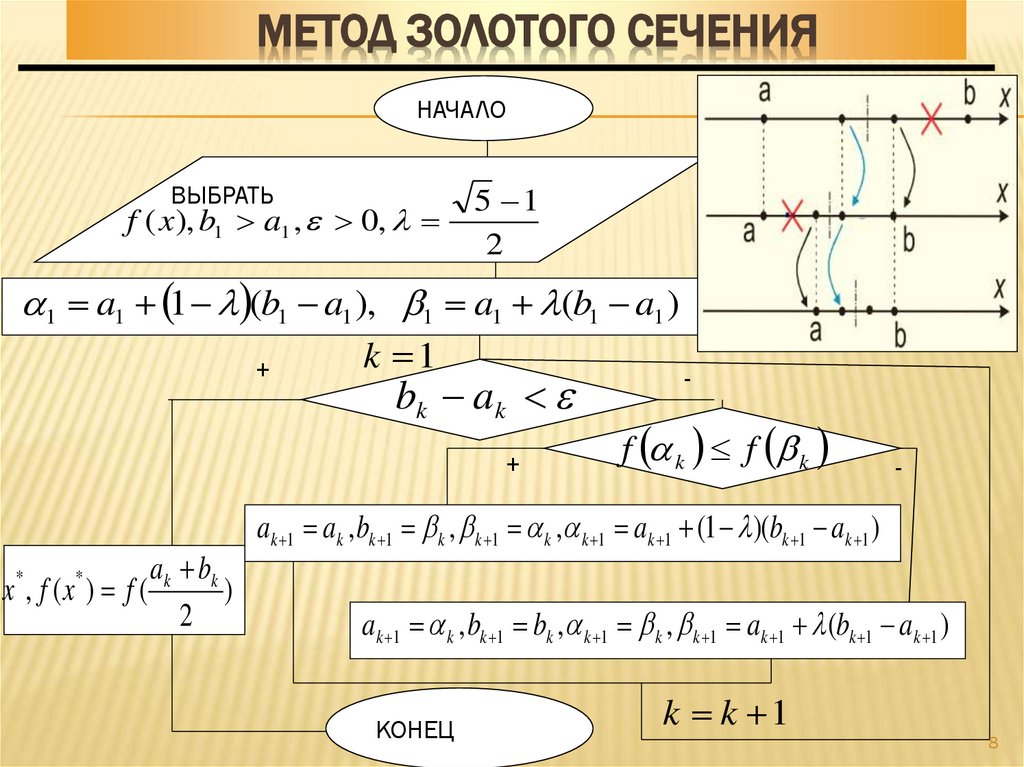
8. Метод золотого сечения

МЕТОД ЗОЛОТОГО СЕЧЕНИЯ
НАЧАЛО
ВЫБРАТЬ
f ( x), b1 a1 , 0,
5 1
2
1 a1 1 (b1 a1 ), 1 a1 (b1 a1 )
k 1
+
bk ak
+
ak bk
x , f (x ) f (
)
2
*
-
f k f k
-
ak 1 ak , bk 1 k , k 1 k , k 1 ak 1 (1 )(bk 1 ak 1 )
*
ak 1 k , bk 1 bk , k 1 k , k 1 ak 1 (bk 1 ak 1 )
КОНЕЦ
k k 1
8

9.

«Золотым сечением» отрезка называется деление отрезка на две части так, что
отношение длин всего отрезка к длине больше части равно отношению длин
большей части к меньшей
b a b y
b y
y a
Золотое сечение отрезка производит две симметрично расположенные точки
a (1 )(b a), a (b a),
V ( h)
4
(27 h h 3 ) max, 0 h 3 3
a
5 1
2
b
x
9

10.

11. Метод Фибоначчи

МЕТОД ФИБОНАЧЧИ
НЕДОСТАТКИ
1) Надо хранить избыточный набор чисел Фибоначчи либо
многократно генерировать числа по мере необходимости; необходимость
предварительной оценки требуемого числа итераций;
2) Метод Фибоначчи нелегко приспособить к часто используемому критерию
останова, требующему, чтобы значения функции на окончательном интервале
неопределенности разнились на величину меньше заданной погрешности
Метод Фибоначчи основан на последовательности Фибоначчи, которая
определяется следующим образом: F k 1 F k 1 F k , k 1,2,..., F 0 F 1 1
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597...
n
n
1 1 5
10 5
F n 5 2 2 , где n 1,2,...

12. Метод Фибоначчи

МЕТОД ФИБОНАЧЧИ
НАЧАЛО
ВЫБРАТЬ
f ( x), b1 a1 , 0, 0, n : Fn
1 a1
b1 a1
Fn 1
Fn 2
F
(b1 a1 ), 1 a1 n 1 (b1 a1 )
Fn
Fn 1
+
k 1
f k f k
-
Fn k 1
ak 1 k , bk 1 bk , k 1 k , k 1 ak 1
(bk 1 ak 1 )
Fn k 1
Fn k 2
ak 1 ak , bk 1 k , k 1 k , k 1 ak 1
(bk 1 ak 1 )
Fn k
-
k k 1
k n 2
+
n an 1 , n n
f n f n
+
-
an n , bn bn 1
an an 1 , bn n
an bn
x , f (x ) f (
)
2
*
*
КОНЕЦ
12

13.

14. Работа: «Методы одномерного поиска»

РАБОТА: «МЕТОДЫ ОДНОМЕРНОГО ПОИСКА»
Ознакомиться с методами одномерного поиска. Сравнить
ЦЕЛЬ РАБОТЫ
различные алгоритмы по эффективности на тестовых примерах.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
ВАРИАНТЫ
ТЕСТОВЫХ
ЗАДАНИЙ
F( x) ( 0.5 x N ) exp
3
x
4
N 1 5
0,00 N
x 20,2 N 1
14

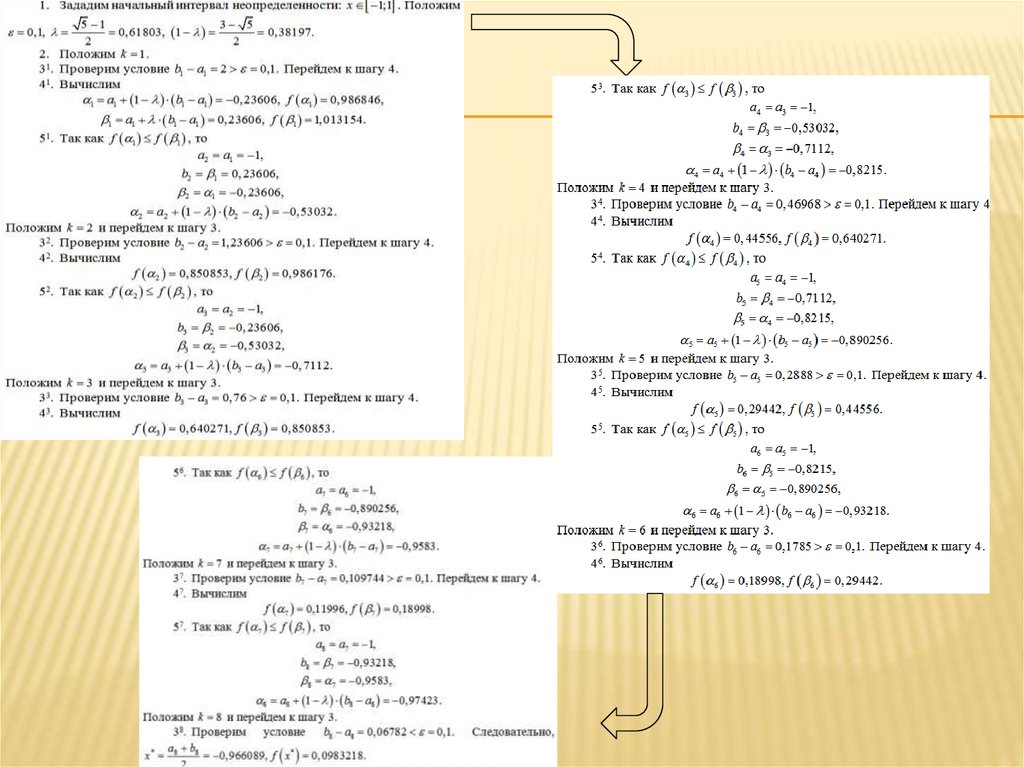
15. Пример

ПРИМЕР
V ( h)
(27 h h ) min, 0 h 3 3
3
4
отрезок
число
итераций
h
V(h)
Метод половинного
деления
[2,999786962
89063,3,0012
564453125]
13
3,000204
42,4115
Метод золотого
сечения
[2,999468304
59553,3,0009
2447922231]
18
2,999918
42,4115
Метод Фибоначчи
[2,998568311
56195,3,0023
8062713257]
16
2,999796
42,4115
27
h 3, V (h)
2
15

16.

А.В. Аттетков, С.В. Галкин,
В.С. Зарубин
МЕТОДЫ
ОПТИМИЗАЦИИ
М.Э.АББАСОВ
МЕТОДЫ ОПТИМИЗАЦИИ
СОДЕРЖАНИЕ ОТЧЕТА
-
титульный лист; цель работы; задание;
таблицы с результатами исследований по каждому методу, где должны быть
отражены границы и длины интервалов на каждой итерации; соотношение
длины интервала на k +1 итерации к длине интервала на k итерации;
график зависимости количества вычислений целевой функции от логарифма
задаваемой точности;
- выводы по всем пунктам задания.
16